Как найти длину средней линии квадрата

Всем привет,мои юные и не очень любители пошуршать мозгами! 🧠

Сегодня поговорим о задачах с фигурами,но не простыми,а на квадратной решетке. 🤓

Такого рода задачи часто попадаются на ОГЭ,поэтому рекомендую дочитать ЭТО ЧУДО до конца 🙂

Длина средней линии трапеции

Решим задачу с этой самой длиной. На клетчатой бумаге 1×1 изображена вот такая трапеция:

Найдем длину ее средней линии.

Сосчитаем клеточки оснований:

7 снизу,3 сверху.

Их складываем.

А потом делим ответ на 2:

Ответ: 5

Расстояние от и до

Теперь про более странную задачу поговорим.

На клетчатой бумаге 1×1 отмечены три точки: A,B и C.

Нужно найти расстояние от точки A до середины отрезка BC.

Нужно ПРОСТО сосчитать три клетки до середины! ВСЕ!

Ответ: 3

Площадь ромба

На той же бумаге начертили ромб.

Нужно найти его площадь.

Как? Оч просто!

Нужно сделать из этого ромба прямоугольник:

А теперь посчитаем клеточки у сторон:

Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей.

Ответ: 20.

Площадь странной фигуры

На этой же (ОПЯТЬ?!ААА!) бумаге Вася начертил странную фигуру. А мы должны найти ее площадь…)

Теперь внимание! Нужно просто посчитать квадратики! Считаем…

Ответ: 11

Длина большей диагонали ромба

Опять ромб. Только теперь нужно найти не площадь,а длину большей диагонали.

Давайте посчитаем:

Ответ: 8

Повторим расстояния…

Опять нужно найти расстояние от точки А,до прямой BC.

Проведем прямую от точки между точками B и C.

А теперь проведем линию от точки A,до отрезка ВС.

Ответ: 1

Площадь параллелограмма

Найдем площадь параллелограмма.

Как ее искать?

Нужно умножить высоту на основание:

Ответ: 20

Длина средней линии треугольника

У нас есть вот такой треугольник:

Нужно найти длину его средней линии,параллельной стороне AC.

Для этого мы узнаем длину основания и разделим ее на 2.

Ответ: 2

Длина большего катета

Нам дан такой прямоугольный треугольник:

Нужно найти длину его большего катета.

Вспомним про стороны прямоугольного треугольника:

Катет b (основание) больше. Он имеет 10 клеток,а катет а 5.

Ответ: 10.

На этом все!

Ждите более сложные задания в следующем посте!

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2021 года; проверки требуют 16 правок.

Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.

Средняя линия треугольника[править | править код]

Средняя линия треугольника — отрезок, соединяющий середины боковых сторон этого треугольника^[1].

Свойства[править | править код]

• средняя линия отсекает треугольник, подобный и гомететичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
• три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
• Если из двух вершин треугольника провести сразу две пары биссектрис (две внутренние и две внешние), а затем на четыре полученные биссектрисы ортогонально спроектировать третью вершину, тогда полученные четыре точки проекций вершины на биссектрисы будут лежать на одной прямой (коллинеарными)^[2]. Эта прямая является средней линией треугольника, параллельной той стороне, концами которой являются упомянутые выше две вершины. Точнее, часть этой средней линии оказывается её продолжением за пределы треугольника.

Признаки[править | править код]

• Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок — средняя линия.

Средняя линия четырёхугольника[править | править код]

Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.

Свойства[править | править код]

Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.

• Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
• Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
• Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
• Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
• Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
• В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.

Средняя линия трапеции[править | править код]

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

Она рассчитывается по формуле: , где AD и BC — основания трапеции.

Свойства[править | править код]

• средняя линия параллельна основаниям
• средняя линия равна полусумме оснований
• средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1] Архивная копия от 12 августа 2017 на Wayback Machine

См. также[править | править код]

• Теорема Вариньона (геометрия)

Примечания[править | править код]

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

• Четырехугольник (общее для всех четырехугольников)

• Квадрат

• Прямоугольник

• Параллелограмм

• Ромб

• Трапеция

• Треугольник

• Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства четырехугольника:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат —  правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a²или S=d²/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d/2 или R=a√(2)/2
Радиус вписанной окружности: r=a/2

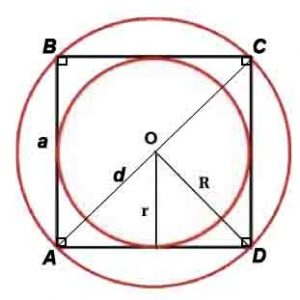где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства квадрата:

• Все стороны равны, все углы равны и составляют 90°;
• Диагонали квадрата равны и перпендикулярны;
• У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
• Квадрат является одновременно частным случаем ромба и прямоугольника

Калькулятор для квадрата поможет вычислить все характеристики квадрата по одной из известных величин. .

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S =  d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a²+b²) (теорема Пифагора)
Радиус описанной окружности: R= √(a²+b²)/2 (теорема Пифагора)

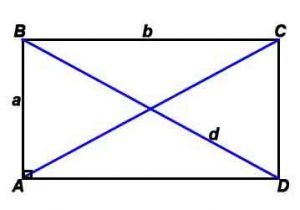где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a²+b²) – корень квадратный из (a²+b²).

Свойства прямоугольника:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

.

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁)²+(d₂)²=(a²+b²)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте:  S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними:  S=(d₁*d₂)/2*sin γ

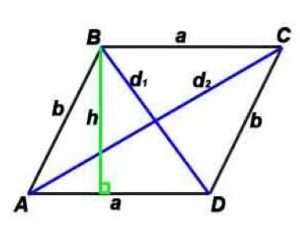где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства параллелограмма:

• У параллелограмма противоположные стороны равны и противоположные углы равны.
• Сумма любых двух соседних углов параллелограмма равна 180°.
• Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
• Каждая диагональ делит параллелограмм на два равных треугольника.
• Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
• Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
• Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или  r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a² · sin α

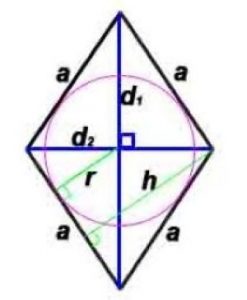где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба

Свойства ромба:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

• Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
• Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.  
• Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме.
• Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
• Равнобокая трапеция – трапеция, у которой боковые стороны равны (c=d). У равнобокой трапеции: диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
• Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

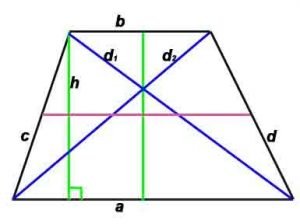где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства трапеции:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними:  S=(a*b)/2* sin γ
                        по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
                        по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c²=a²+b² (Теорема Пифагора)

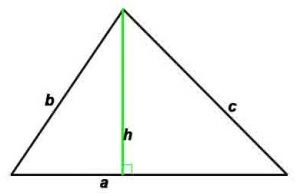где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ  — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности.

Для нахождения характеристик простого, равнобедренного или равностороннего треугольника, воспользуйтесь калькулятором для треугольника.

Чтобы вычислить все характеристики прямоугольного треугольника, воспользуйтесь калькулятором для прямоугольного треугольника.

Свойства треугольника:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:
  |a-b| <c<a+b
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b² (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r² или S = π*d²/4

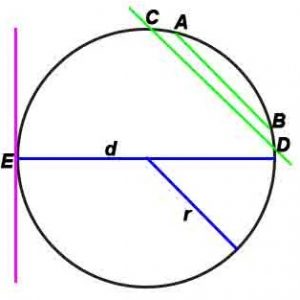где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Калькулятор для окружности и круга поможет вычислить все характеристики круга по одной из известных величин.

В заключении

Весь курс начальной школы (за 1-4 классы) в краткой форме на сайте edu.intmag24.ru. С помощью курса можно быстро повторить основные моменты и правила по предметам: русский язык, математика, окружающий мир.

Прочитайте внимательно текст и выполните задания №1-5.

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.

---

Задание №1

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.

Объекты	яблони	теплица	сарай	жилой дом
Цифры

Решение

Для решения 1 задачи работаем с текстом и планом одновременно:

при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж – 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.

Итак, получили следующее:

1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.

Заполняем нашу таблицу:

Объекты	яблони	теплица	сарай	жилой дом
Цифры	3	5	1	7

Записываем ответ: 3517

---

Задание №2

Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?

Решение

Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.

Ответ: 11

---

Задание №3

Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Ответ: 4

---

Задание №4

Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.

Решение

Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина – 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м

Ответ: 48

---

Задание №5

Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.

Номер магазина	Расход краски	Масса краски в одной банке	Стоимость одной банки краски	Стоимость доставки заказа
1	0,25 кг/кв.м	6 кг	3000 руб.	500 руб.
2	0,4 кг/кв.м	5 кг	1900 руб.	800 руб.

Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?

Решение

Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:

1 магазин: 232х0,25=58 кг

2 магазин: 232х0,4=92,8 кг

Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:

1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)

2 магазин: 92,8:5=18,56; значит надо 19 банок.

Вычислим стоимость краски в каждом магазине плюс доставка:

1 магазин: 10х3000+500=30500 руб.

2 магазин: 19х1900+800=36900 руб.

Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.

Ответ: 30500

Ответ: см. решение