Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.
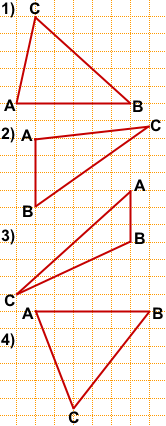
Задача 1
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
Решение:
Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.
Но задача легко разрешима с применением свойства средней линии треугольника:
средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.
Длина искомой средней линии равна её половине.
1) AB=6,
![]()
![]()
![]()
![]()
А как быть, если длину стороны треугольника посчитать по клеточкам не получается?
Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.
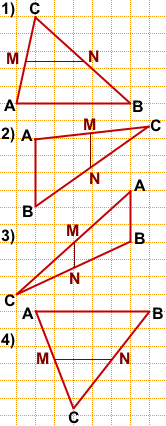
Задача 2
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
Решение:
 1)В прямоугольном треугольнике ABC AB — гипотенуза.
1)В прямоугольном треугольнике ABC AB — гипотенуза.
AC=4, BC=3.
По теореме Пифагора
![]()
![]()
Средняя линия MN равна половине гипотенузы:
![]()
2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.
По теореме Пифагора
![]()
![]()
![]()
Всего: 46 1–20 | 21–40 | 41–46
Добавить в вариант
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
Всего: 46 1–20 | 21–40 | 41–46
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки ![]() изображена трапеция. Найдите длину средней линии этой трапеции.
изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна
Тогда

Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки ![]() Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
![]() , где
, где и
— диагонали.
Получим: ![]()
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки ![]() Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:
![]()
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
![]()
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны
и
. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
.
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
.
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки ![]()

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки ![]()

Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
![]()
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 – 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна
.

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как
. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как
), а длина дуги данного сектора равна
, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть
градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть
круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в
раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Всем привет!
До ОГЭ по математике осталось совсем немного времени, но с другой стороны его не так уж и мало, чтобы успеть подготовиться и получить хороший результат на экзамене!
С этой статье мы разберем, как решать одно из самых простых заданий по математике, а именно №18. Кроме того, это задание относится к блоку “Геометрия”, а для того, чтобы успешно сдать ОГЭ, необходимо набрать как минимум два балла по геометрии! И спомощью этого задания вы уже получите как минимум один балл))
Даже если вам тяжело дается геометрия, это задание сможет решить каждый школьник..нужно просто повторить немного теории и научиться пользоваться некоторыми формулами, которые будут вам доступны на экзамене в форме справочных материалов.
В качестве примеров я взяла 5 заданий из сборника Ященко для подготовке к ОГЭ 2023. Итак, поехали.
Задание 1
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до отрезка BC.
Здесь все просто – расстояние от точки до прямой – это перпендикуляр, проведенный к этой прямой. Поэтому соединяем точки В и С в отрезок ВС, проводим к нему перпендикуляр из точки А. Считаем длину его по клеточкам:
Задание 2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Для того, чтобы найти площадь трапеции, необходимо вспомнить формулу нахождения площади. Но на экзамене выдаются справочные материалы, поэтому найти эту формулу не составит никакого труда:
Осталось расшифровать эту формулу:
a и b – это основания трапеции, h -высота трапеции. Дальше считаем все по клеточкам и подставляем полученные значения в формулу:
Задание 3
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
Здесь, как и в предыдущем задании, мы можем воспользоваться справочными материалами и найти формулу площади треугольника.
В этом задании используем 1 формулу, где а – это основание треугольника, h – высота, проведенная к основанию. В качестве основания мы берем сторону, расположенную слева, так как ее можно посчитать точно по клеточкам, соответственно и высоту проводим к этой стороне. Далее считаем клетки, подставляем в формулу и вычисляем площадь.
Задание 4
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. … Найдите длину его средней линии, параллельной стороне AC.
Для решения этой задачи необходимо знать формулу нахождения средней линии. Но и здесь нам помогут справочные материалы. Там эта формула конечно же есть, даже если вы впервые слышите о таком понятии, как средняя линия, здесь все предельно ясно: нужно нижнее основание треугольника разделить на 2.
Остается только посчитать длину нижнего основания по клеточкам и разделить полученное значение на два.
Задание 5
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Находим формулу площади ромба в справочных материалах:
Далее считаем диагонали ромба по клеточкам, подставляем полученные значения в формулу площади и вычисляем площадь ромба:
Видеоразбор других прототипов 18 задания можно посмотреть здесь:
Подписывайтесь на канал, чтобы успешно подготовиться к ОГЭ 2023!
Если статья была полезна, не забудьте поставить лайк, это очень поможет ее продвижению!
Пишите в комментариях, какие еще задания ОГЭ подробно разобрать?
Средняя линия треугольника на клетчатой бумаге
Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.
Но задача легко разрешима с применением свойства средней линии треугольника:
средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.
Длина искомой средней линии равна её половине.
А как быть, если длину стороны треугольника посчитать по клеточкам не получается?
Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
1)В прямоугольном треугольнике ABC AB — гипотенуза.
По теореме Пифагора
Средняя линия MN равна половине гипотенузы:
2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.
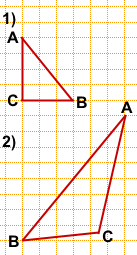
Решение №1689 На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
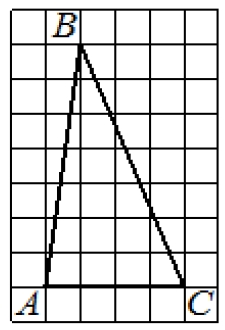
Источник задания: yagubov.ru
Средняя линяя равна половине основания. Основание АС равно 4 клетки, значит средняя линяя параллельная этому основанию равна:
Ответ: 2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Как найти среднюю линию треугольника?

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
- Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
- Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
- Тупоугольный. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, которой параллельна средняя линия.
Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия равна половине длины основания и параллельна ему.
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
По условию нам дано, что MA = MB, NA = NC
Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
(по второму признаку подобия треугольников).
△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.
△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.
Параллельность средней линии и соответствующего ей основания доказана.
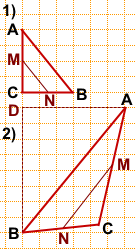
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.
Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника ΔMNK равен 10.
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.
Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:
Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:
Значит, AC = 2MN = 2 × 3 = 6.
Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:
Значит, BC = 2NP = 2 × 4 = 8.
Тогда найдем площадь большого треугольника, используя формулу, указанную выше:
S = ½ × 6 × 8 = ½ × 48 = 24.
Ответ: площадь большого прямоугольного треугольника равна 24.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kak-najti-srednyuyu-liniyu-treugolnika
[/spoiler]
