Одно из важных следствий раздела специальной теории относительности – вывод об относительности расстояний. Определение этому понятию звучит следующим образом.
Расстояние – это не абсолютная величина, зависящая от скорости движения тела применительно к заданной системе отсчета.
Обозначим длину твердого стержня, измеренную в собственной системе отсчета, где стержень неподвижен, как l0. А также обозначим длиной l стержня в другой системе отсчета, в которой стержень движется со скоростью υ. Длина l – это расстояние между концами стержня, которые зафиксированы одновременно по часам данной системы отсчета. В соответствии с теорией относительности справедливо следующее равенство:
l-l01-β2=l0γ, где γ=11-β2>1, β=υc
Получается, что длина движимого стержня всегда меньше, чем длина недвижимого стержня.
Относительность расстояний (длин) зависит от постоянства скорости света в инерциальных системах и от промежутков времени.
Компьютерный эксперимент измерения относительности расстояний
Представим компьютерную модель, которая проводит эксперимент измерения длины твердого стержня 2-мя наблюдателями из различных инерциальных систем. При этом один наблюдатель находится в неподвижном состоянии по отношению к стержню, а второй передвигается со скоростью υ вдоль стержня. Эксперимент заключается в замере времени распространения светового импульса от одного конца стержня к другому и в обратную сторону. Обозначим событие 1, как короткую световую вспышку на одном конце стержня и событие 2, как возвращение светового импульса к лампе. Временной интервал в своей системе отсчета между 2-мя событиями равняется
τ0 =2l0c.
В движимой системе отсчета временной интервал между 2-мя событиями равняется
τ=lc-υ+lc+υ.
Из этого следует
l=l0·τ0τ=l0γ.
С помощью компьютерных экспериментов можно менять относительную скорость систем отсчета. На экране вверху демонстрируется эксперимент измерения собственного времени τ0 между событиями системы, где стержень недвижим. А внизу экрана такой же самый эксперимент выполняет наблюдатель с подвижным стержнем в собственной системе отсчета. Результаты эксперимента, а именно значения времени τ0 и τ отображаются на часах в одной и второй системах отсчета.
Рассмотрим относительность расстояний более подробно.
Измерение длины движущегося стержня
Допустим, твердый стержень неподвижен в системе отсчета K’, которая движется со скоростью υ относительно системы отсчета K (рис. 4.3.1). Стержень находится параллельно оси x’.
Длина стержня замерена эталонной линейкой в системе K’ и равняется l0. Её именуют, как собственная длина.
Какова длина данного стержня, если ее захочет измерить наблюдатель в системе K?
Известно, что длина l стержня в системе K, относительно которой передвигается стержень, – это расстояние между координатами концов стержня, отмеченными одновременно по часам данной системы. Если мы знаем скорость системы K’ по отношению к системе K, тогда измерение длины движущегося стержня сводится к измерению временного интервала: длина l стержня, движущегося со скоростью υ, равняется произведению υτ0 , где τ0 – это временной интервал по часам в системе K между началом стержня и его конца мимо какой-то неподвижной точки (к примеру, точки A) в системе K (рис. 4.3.1). Поскольку в системе K оба события – прохождение начала (событие 1) и конца (событие 2) стержня мимо фиксированной точки A – происходят в одной и той же точке, тогда временной промежуток τ0 в системе K – это собственное время. Таким образом, длина l движущегося стержня равняется l=υτ0.
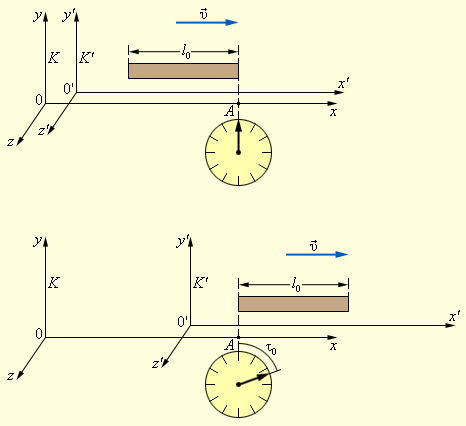
Рисунок 4.3.1. Измерение длины движущегося стержня.
Сейчас выведем связь между l и l0. С позиции наблюдателя в системе K’, точка A, которая принадлежит системе K, передвигается вдоль неподвижного стержня в левую сторону со скоростью υ, поэтому можно записать следующее утверждение:
l0=υτ,
где τ – это временной промежуток между моментами прохождения точки A мимо концов обоих стержня, который измерен по синхронизованным часам в системе K’. Зная зависимость между промежутками времени τ и τ0: τ=τ01-β2, запишем следующую формулу:
l=l01-υ2c2=l01-β2
Относительность длины стержня
Получается, что длина стержня зависит от собственной системы отсчета, в которой измеряется, то есть является относительной величиной. Длина стержня наибольшая там, где стержень находится в состоянии покоя. Подвижные по отношению к наблюдателю тела сокращаются по направлению собственного движения. Данный релятивистский эффект получил название лоренцево сокращение длины.
Мы выяснили, что расстояние – это относительная величина, которая зависит от скорости движения тела в заданной системе отсчета. Сокращение длины не зависит от каких-либо процессов, происходящих в самих телах. Лоренцево сокращение описывает изменение размера подвижного тела по направлению его движения. Если стержень на рис. 4.3.1 положить перпендикулярно оси x (вдоль нее движется система K’), то длина стержня будет одинакова для наблюдателей двух систем K и K’. Таким образом, всех инерциальные системы равноправны.
Представим мысленно следующий эксперимент. Положим в измерительных системах K и K’ вдоль осей y и y’ два жестких стержня. При этом у стержней одинаковые собственные длины l, которые измерены двумя неподвижными по отношению к каждому из стержней наблюдателями в системах K и K’, и один из концов каждого стержня совпадает с началом координат O или O’. В какой-то момент времени стержни оказываются рядом друг с другом и появляется возможность сравнить их: конец каждого стержня может сделать метку на другом стержне. Если бы данные метки не совпали с концами стержней, то один из них оказался бы длиннее другого с точки зрения обеих систем отсчета. А это бы шло вразрез с принципом относительности.
Обращаем внимание, что при маленьких скоростях движения (υ≪c) формулы СТО преобразуются в классические соотношения: l≈l0 и τ≈τ0. Так, классические представления, которые лежат в основе механики Ньютона и которые сформировали на основе многолетнего опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при β=υс→0. Здесь прослеживается принцип соответствия.
Сравним длину стержня в инерциальных системах отсчета K и K’ (рис.7.4.1). Предположим, что стержень, расположенный вдоль совпадающих осей x и x’ покоится всистеме K’. Тогда определение его длины в этой системе не доставляет хлопот. Нужно приложить к стержню масштабную линейку и определить координату x’1 одного конца стержня, а затем координату x’2 другого конца. Разность координат даст длину стержня l0 в системе K’: l0=x’2-x’1.

рис 7.4.1
Стержень покоится в системе K’. Относительно системы K он движется со скоростью v, равной относительной скорости систем V.
В системе K дело обстоит сложнее. Относительно этой системы стержень движется со скоростью v, равной скорости V, с которой система K’ движется относительно системы K. (Обозначение V мы будем употреблять только применительно к относительной скорости систем отсчета.) Поскольку стержень движется, нужно произвести одновременный отсчет координат его концов x1 и x2 в некоторый момент времени t. Разность координат даст длину стержня в системе K: l=x2-x1
Для сопоставления длин l и l0 нужно взять ту из формул преобразований Лоренца, которая связывает координаты x, x’ и время t системы K, т. е. первую из формул (7.3.13). Подстановка в нее значений координат и времени приводит к выражениям
Отсюда
 |
(7.4.2) |
(мы подставили вместо ![]() его значение). Заменив разности координат длинами стержня, а относительную скорость V систем K и K’ равной ей скоростью стержня v, с которой он движется в системе K, придем к формуле
его значение). Заменив разности координат длинами стержня, а относительную скорость V систем K и K’ равной ей скоростью стержня v, с которой он движется в системе K, придем к формуле
| (7.4.3) |
Таким образом, длина движущегося стержня оказывается меньше той, которой обладает стержень в состоянии покоя. Аналогичный эффект наблюдается для тел любой формы: в направлении движения линейные размеры тела сокращаются тем больше, чем больше скорость движения Это явление называется лоренцевым (или фицджеральдовым) сокращением. Поперечные размеры тела не изменяются. В результате, например, шар принимает форму эллипсоида, сплющенного в направлении движения. Можно показать, что зрительно этот эллипсоид будет восприниматься в виде шара. Это объясняется искажением зрительного восприятия движущихся предметов, вызванным неодинаковостью времен, которые затрачивает свет на прохождение пути от различно удаленных точек предмета до глаза.
Искажение зрительного восприятия приводит к тому, что движущийся шар воспринимается глазом как эллипсоид, вытянутый в направлении движения. Оказывается, что изменение формы, обусловленное лоренцевым сокращением, в точности компенсируется искажением зрительного восприятия.
Последнее изменение: Вторник, 11 марта 2014, 22:28
2.2.3. Собственная длина и собственный объем[править]
Рассмотрим стержень, который покоится в системе отсчета К и параллельный оси «х». Длина стержня в системе К может быть вычислена:

Найдем длину этого стержня в системе отсчета K’, которая движется относительно К с постоянной скоростью V.

По определению, «собственной длиной» стержня называется его длина в той системе, в которой стержень покоится.
Обозначим собственную длину неподвижного стержня 


Как видно, самую большую длину стержень имеет в той системе отсчета, в которой он покоится. При движении длина уменьшается, этот эффект называют «Лоренцевым сокращением».
Из выражений (2.2.11) легко показать, что поперечные размеры тела не изменяются при движении вдоль оси «х». Это означает, что объем тела меняется точно так же, как и его длина:

где V0 — это «собственный объем» тела.
См. также[править]
<<Назад | Далее>>
Оглавление
Примечания[править]
nitrino – 10 ноября, 2011 – 11:57
Имеется стержень, который двигается с постоянным ускорением мимо двух пунктов наблюдения (ПН), которые фиксируют время прохода начала и конца стержня. Расстояние между ПН (L) известно, моменты прохода начала и конца стержня через ПН (t1нач, t1кон, t2нач, t2кон) известны. Необходимо определить длину стержня и с каким ускорением он двигался.
Предложили решить задачу друзья “на слабо”, как я понял, задача с олимпиады для старших классов в средней школе в Екатеринбурге, точнее не могу сказать. Помогите не ударить в грязь лицом 🙂
Теги:
- кинематика
- механика
- равноускоренное движение
- задачи с подсказками
- версия для печати
![]()
Относительность промежутков времени (замедление времени)Промежуток времени между двумя событиями имеет наименьшее значение в системе отсчета, связанной с движущимся объектом, где происходит исследуемое явление, которое определяется по формуле . Эту формулу легко получить из преобразований Лоренца, учитывая, что Δt=t2-t1, а Δt0=t’2-t’1 Из этой формулы следует, что длительность одного и того же процесса различна в системах K и K1. В системе K1 длительность процесса больше. Следовательно, он протекает медленнее, чем в системе К Время, отсчитываемое по часам, которые движутся вместе с телом, называютсобственным временем. Оно самое короткое; наблюдается релятивистский эффект замедления времени (Δ t > Δ to).

Например, если космонавты отправляются к звездной системе (и обратно), находящейся на расстоянии 500 световых лет от Земли, со скоростьюv=0,9999c, то на это потребуется по их часам 14,1 года; в то время как на Земле пройдет 10 веков.
Этот результат является основой “парадокса близнецов” в СТО. Пусть один из двух близнецов решает стать космонавтом и летит на корабле со скоростьюv относительно Земли. Тогда по возвращении он окажется младше своего брата, все время остававшегося на Земле.
С другой стороны, так как все ИСО равноправны, можно считать, что Земля двигалась относительно корабля с той же скоростью. Тогда помолодеть должен другой близнец. Разрешить парадокс можно, если понять, что на самом деле системы, связанные с Землей и кораблем неравноправны, т.
к. корабль не все время являлся ИСО (в процессах старта, поворота, приземления он двигался с ускорением). Процессы в неинерциальных СО рассматриваются в общей теории относительности, где доказывается, что на самом деле Δ t > Δ to. Релятивистское замедление времени экспериментально подтверждено в опытах с распадом некоторых элементарных частиц (мюонов).
Одно из важных следствий раздела специальной теории относительности – вывод об относительности расстояний. Определение этому понятию звучит следующим образом. Расстояние – это не абсолютная величина, зависящая от скорости движения тела применительно к заданной системе отсчета.
Определение 1
Обозначим длину твердого стержня, измеренную в собственной системе отсчета, где стержень неподвижен, как
l
. А также обозначим длиной
l
стержня в другой системе отсчета, в которой стержень движется со скоростью
υ
. Длина
l
– это расстояние между концами стержня, которые зафиксированы одновременно по часам данной системы отсчета. В соответствии с теорией относительности справедливо следующее равенство:
llβlγ
, где
γββυc
Получается, что длина движимого стержня всегда меньше, чем длина недвижимого стержня.
Относительность расстояний (длин) зависит от постоянства скорости света в инерциальных системах и от промежутков времени.
Компьютерный эксперимент измерения относительности расстояний
Представим компьютерную модель, которая проводит эксперимент измерения длины твердого стержня -мя наблюдателями из различных инерциальных систем. При этом один наблюдатель находится в неподвижном состоянии по отношению к стержню, а второй передвигается со скоростью
υ
вдоль стержня. Эксперимент заключается в замере времени распространения светового импульса от одного конца стержня к другому и в обратную сторону. Обозначим событие , как короткую световую вспышку на одном конце стержня и событие , как возвращение светового импульса к лампе. Временной интервал в своей системе отсчета между -мя событиями равняетсяτ02l0c.
В движимой системе отсчета временной интервал между -мя событиями равняетсяτlcυlcυ.
Из этого следуетll0τ0τl0γ.
С помощью компьютерных экспериментов можно менять относительную скорость систем отсчета. На экране вверху демонстрируется эксперимент измерения собственного времени
τ
между событиями системы, где стержень недвижим. А внизу экрана такой же самый эксперимент выполняет наблюдатель с подвижным стержнем в собственной системе отсчета. Результаты эксперимента, а именно значения времени
τ
и
τ
отображаются на часах в одной и второй системах отсчета.

Рассмотрим относительность расстояний более подробно.
[custom_ads_shortcode1]
Измерение длины движущегося стержня
Допустим, твердый стержень неподвижен в системе отсчета
K
, которая движется со скоростью υ относительно системы отсчета
K
(рис.
). Стержень находится параллельно оси
x
.
Определение 2
Длина стержня замерена эталонной линейкой в системе
K
и равняется
l
. Её именуют, как собственная длина.
Какова длина данного стержня, если ее захочет измерить наблюдатель в системе
K
?
Известно, что длина
l
стержня в системе
K
, относительно которой передвигается стержень, – это расстояние между координатами концов стержня, отмеченными одновременно по часам данной системы. Если мы знаем скорость системы
K
по отношению к системе
K
, тогда измерение длины движущегося стержня сводится к измерению временного интервала: длина
l
стержня, движущегося со скоростью
υ
, равняется произведению
υτ
, где
τ
– это временной интервал по часам в системе
K
между началом стержня и его конца мимо какой-то неподвижной точки (к примеру, точки
A
) в системе
K
(рис.
). Поскольку в системе
K
оба события – прохождение начала (событие ) и конца (событие ) стержня мимо фиксированной точки
A
– происходят в одной и той же точке, тогда временной промежуток
τ
в системе
K
– это собственное время. Таким образом, длина
l
движущегося стержня равняется
lυτ
.
Рисунок 431 Измерение длины движущегося стержня.
Сейчас выведем связь между
l
и
l
. С позиции наблюдателя в системе
K
, точка
A
, которая принадлежит системе
K
, передвигается вдоль неподвижного стержня в левую сторону со скоростью υ, поэтому можно записать следующее утверждение:
lυτ
,где τ – это временной промежуток между моментами прохождения точки A мимо концов обоих стержня, который измерен по синхронизованным часам в системе K. Зная зависимость между промежутками времени τ и τ0: ττ01β2, запишем следующую формулу:
llυclβ
[custom_ads_shortcode2]
Относительность длины стержня
Определение 3
Получается, что длина стержня зависит от собственной системы отсчета, в которой измеряется, то есть является относительной величиной. Длина стержня наибольшая там, где стержень находится в состоянии покоя. Подвижные по отношению к наблюдателю тела сокращаются по направлению собственного движения. Данный релятивистский эффект получил название лоренцево сокращение длины.
Мы выяснили, что расстояние – это относительная величина, которая зависит от скорости движения тела в заданной системе отсчета. Сокращение длины не зависит от каких-либо процессов, происходящих в самих телах. Лоренцево сокращение описывает изменение размера подвижного тела по направлению его движения. Если стержень на рис.
положить перпендикулярно оси
x
(вдоль нее движется система
K
), то длина стержня будет одинакова для наблюдателей двух систем
K
и
K
. Таким образом, всех инерциальные системы равноправны.
Доказательство 1
Представим мысленно следующий эксперимент. Положим в измерительных системах
K
и
K
вдоль осей
y
и
y
два жестких стержня. При этом у стержней одинаковые собственные длины
l
, которые измерены двумя неподвижными по отношению к каждому из стержней наблюдателями в системах
K
и
K
, и один из концов каждого стержня совпадает с началом координат
O
или
O
. В какой-то момент времени стержни оказываются рядом друг с другом и появляется возможность сравнить их: конец каждого стержня может сделать метку на другом стержне. Если бы данные метки не совпали с концами стержней, то один из них оказался бы длиннее другого с точки зрения обеих систем отсчета. А это бы шло вразрез с принципом относительности. Обращаем внимание, что при маленьких скоростях движения υc формулы СТО преобразуются в классические соотношения: ll0 и ττ0. Так, классические представления, которые лежат в основе механики Ньютона и которые сформировали на основе многолетнего опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при βυс0. Здесь прослеживается принцип соответствия.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter.
Пусть твердый стержень покоится в системе отсчета K’, движущейся со скоростью υ относительно системы отсчета K (рис. 4.3.1). Стержень ориентирован параллельно оси x’. Его длина, измеренная с помощью эталонной линейки в системе K’, равна l. Ее называют собственной длиной. Какой будет длина этого стержня, измеренная наблюдателем в системе K? Для ответа на этот вопрос необходимо дать определение процедуры измерения длины движущегося стержня.
Под длиной l стержня в системе K, относительно которой стержень движется, понимают расстояние между координатами концов стержня, зафиксированными одновременно по часам этой системы. Если известна скорость системы K’ относительно K, то измерение длины движущегося стержня можно свести к измерению времени: длина l движущегося со скоростью υстержня равна произведению υτ, где τ – интервал времени по часам в системе K между прохождением начала стержня и его конца мимо какой-нибудь неподвижной точки (например, точки A) в системе K (рис. 4.3.1). Поскольку в системе K оба события (прохождение начала и конца стержня мимо фиксированной точки A) происходят в одной точке, то промежуток времениτ в системе K является собственным временем. Итак, длина l движущегося стержня равна l = υτ.
| Рисунок 4.3.1. Измерение длины движущегося стержня |
Найдем теперь связь между l и l. С точки зрения наблюдателя в системе K’, точка A, принадлежащая системе K, движется вдоль неподвижного стержня налево со скоростью υ, поэтому можно записатьгде τ есть промежуток времени между моментами прохождения точки A мимо концов стержня, измеренный по синхронизованным часам в K’. Используя связь между промежутками времени τ иτ0 , найдем
Таким образом, длина стержня зависит от системы отсчета, в которой она измеряется, т. е. является относительной величиной. Длина стержня оказывается наибольшей в той системе отсчета, в которой стержень покоится. Движущиеся относительно наблюдателя тела сокращаются в направлении своего движения. Этот релятивистский эффект носит название лоренцева сокращения длины.
Расстояние не является абсолютной величиной, оно зависит от скорости движения тела относительно данной системы отсчета. Сокращение длины не связанно с какими-либо процессами, происходящими в самих телах. Лоренцево сокращение характеризует изменение размера движущегося тела в направлении его движения. Если стержень на рис. 4.3.1 расположить перпендикулярно оси x, вдоль которой движется система K’, то длина стержня оказывается одинаковой для наблюдателей в обеих системах K и K’. Это утверждение находится в соответствии с постулатом о равноправии всех инерциальных систем. Для доказательства можно рассмотреть следующий мысленный эксперимент. Расположим в системах K и K’ вдоль осей y и y’два жестких стержня. Стержни имеют одинаковые собственные длины l, измеренные неподвижными по отношению к каждому из стержней наблюдателями в K и K’, и один из концов каждого стержня совпадает с началом координат O или O’. В некоторый момент стержни оказываются рядом и представляется возможность сравнить их непосредственно: конец каждого стержня может сделать метку на другом стержне. Если бы эти метки не совпали с концами стержней, то один из них оказался бы длиннее другого с точки зрения обеих систем отсчета. Это противоречило бы принципу относительности.
Неизменность длины движущегося стержня, ориентированного перпендикулярно направлению движения, была использована в § 4.2 при анализе релятивистского замедления времени.
Следует обратить внимание, что при малых скоростях движения (υ << c) формулы СТО переходят в классические соотношения: l ≈ l и τ ≈ τ. Таким образом, классические представления, лежащие в основе механики Ньютона и сформировавшиеся на основе многовекового опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при β = υ / c → 0. В этом проявляется принцип соответствия.
| Модель. Относительность расстояний |
Предыдущая103104105106107108109110111112113114115116117118Следующая
Дата добавления: 2015-08-11; просмотров: 455; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
[custom_ads_shortcode3]
ПОСМОТРЕТЬ ЕЩЕ:
Пусть твердый стержень покоится в системе отсчета K’, движущейся со скоростью υ относительно системы отсчета K (рис. 4.3.1). Стержень ориентирован параллельно оси x’. Его длина, измеренная с помощью эталонной линейки в системе K’, равна l. Ее называют собственной длиной. Какой будет длина этого стержня, измеренная наблюдателем в системе K? Для ответа на этот вопрос необходимо дать определение процедуры измерения длины движущегося стержня.
Под длиной l стержня в системе K, относительно которой стержень движется, понимают расстояние между координатами концов стержня, зафиксированными одновременно по часам этой системы. Если известна скорость системы K’ относительно K, то измерение длины движущегося стержня можно свести к измерению времени: длина l движущегося со скоростью υ стержня равна произведению υτ, где τ – интервал времени по часам в системе K между прохождением начала стержня и его конца мимо какой-нибудь неподвижной точки (например, точки A) в системе K (рис. 4.3.1). Поскольку в системе K оба события (прохождение начала и конца стержня мимо фиксированной точки A) происходят в одной точке, то промежуток времени τ в системе K является собственным временем. Итак, длина l движущегося стержня равна l = υτ.
| Рисунок 4.3.1. Измерение длины движущегося стержня |
Найдем теперь связь между l и l. С точки зрения наблюдателя в системе K’, точка A, принадлежащая системе K, движется вдоль неподвижного стержня налево со скоростью υ, поэтому можно записатьгде τ есть промежуток времени между моментами прохождения точки A мимо концов стержня, измеренный по синхронизованным часам в K’. Используя связь между промежутками времени τ и τ0 , найдем

Таким образом, длина стержня зависит от системы отсчета, в которой она измеряется, т. е. является относительной величиной.
Длина стержня оказывается наибольшей в той системе отсчета, в которой стержень покоится. Движущиеся относительно наблюдателя тела сокращаются в направлении своего движения. Этот релятивистский эффект носит название лоренцева сокращения длины.
Расстояние не является абсолютной величиной, оно зависит от скорости движения тела относительно данной системы отсчета. Сокращение длины не связанно с какими-либо процессами, происходящими в самих телах. Лоренцево сокращение характеризует изменение размера движущегося тела в направлении его движения.

Если стержень на рис. 4. 3.
1 расположить перпендикулярно оси x, вдоль которой движется система K’, то длина стержня оказывается одинаковой для наблюдателей в обеих системах K и K’. Это утверждение находится в соответствии с постулатом о равноправии всех инерциальных систем. Для доказательства можно рассмотреть следующий мысленный эксперимент.
Расположим в системах K и K’ вдоль осей y и y’ два жестких стержня. Стержни имеют одинаковые собственные длины l, измеренные неподвижными по отношению к каждому из стержней наблюдателями в K и K’, и один из концов каждого стержня совпадает с началом координат O или O’. В некоторый момент стержни оказываются рядом и представляется возможность сравнить их непосредственно: конец каждого стержня может сделать метку на другом стержне.
Если бы эти метки не совпали с концами стержней, то один из них оказался бы длиннее другого с точки зрения обеих систем отсчета. Это противоречило бы принципу относительности.
Неизменность длины движущегося стержня, ориентированного перпендикулярно направлению движения, была использована в § 4.2 при анализе релятивистского замедления времени.
Следует обратить внимание, что при малых скоростях движения (υ << c) формулы СТО переходят в классические соотношения: l ≈ l и τ ≈ τ. Таким образом, классические представления, лежащие в основе механики Ньютона и сформировавшиеся на основе многовекового опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при β = υ / c → 0. В этом проявляется принцип соответствия.

Date: 2015-12-10; view: 58; Нарушение авторских прав
Источники:
- www.eduspb.com
- zaochnik.com
- helpiks.org
- mydocx.ru
