Школьная математика » Блог » Как найти стороны прямоугольника при известных периметре и площади
В этой статье я хочу рассмотреть две математические задачи повышенной сложности для 4 класса.
Видеоурок по теме этой статьи можно посмотреть по ссылке.
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
С этими задачами, я уверен, без труда справится более старший школьник, знакомый с решением системы уравнений и квадратных уравнений. Кстати, подобная задача есть в учебнике по геометрии Атанасяна, глава VI № 454 пункт б за 8 класс.
Но почему же эти задачи указаны в математических сборниках как задачи для 4 класса, в котором еще не изучают алгебраические понятия и методы решения? Нет ли здесь ошибки?
Нет, никакой ошибки здесь нет. Эти, и аналогичные им задачи можно решить и без использования алгебраических знаний.
Первое, что приходит на ум – это по значению периметра прямоугольника (а периметр – это удвоенная сумма двух его сторон) найти сумму двух сторон, а после простым подбором определить два числа, произведение которых равно данной по условию площади прямоугольника, а сумма – половине периметра.
Я хочу показать вам математически точное решение, которое безо всяких подборов приводит к правильному результату.
Нахождение сторон прямоугольника при известных периметре и площади
Рассмотрим первую задачу:
Площадь прямоугольника 32 см2, а периметр – 24 см. Найти стороны прямоугольника.
Как известно, периметр прямоугольника находится по формуле ({color{red} P=2cdot (a+b)}) , площадь – по формуле ({color{red} S=acdot b}) .
Так как периметр прямоугольника – это удвоенное произведение суммы двух сторон прямоугольника, то мы можем найти эту сумму, разделив значение периметра на 2:
({color{red} a + b = 24 : 2 = 12}) см.
А дальше мы рассуждаем так.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – четное число, то очевидно, что прямоугольник с максимально возможным значением площади при сумме его двух сторон, равной 12, – это квадрат со стороной ({color{red} 12 : 2 = 6}) см.
Тогда площадь этого квадрата равна
({color{red}S_{k}=6cdot 6=36}) см2.
По условию нашей задачи площадь прямоугольника составляет 32 см2. Находим разницу между полученной площадью квадрата и заданной площадью прямоугольника.
({color{red} S–S _{k}=36-32=4}) см2.
Это значит, что нам нужно изменить стороны рассматриваемого квадрата со стороной 6 см так, чтобы уменьшилась его площадь, но не изменился периметр.
Так как квадрат имеет самую большую площадь среди прямоугольников с одинаковым периметром, то для уменьшения площади нам нужно увеличить разницу между его длиной и шириной. То есть, ширину уменьшить, а длину увеличить на одно и то же число.
Но на какое?
Площадь 4 см2 – это квадрат со стороной 2 см. Это и есть нужное нам число.
Тогда, ширина искомого прямоугольника будет равна:
({color{red} a=6-2=4}) см
а длина:
({color{red} b=6+2=8}) см.
Проверим найденные длины сторон, определив периметр и площадь полученного прямоугольника:
({color{red} P=2cdot (4+8)=2cdot 12=24}) см
({color{red} S=4cdot 8=32}) см2.
Задача решена верно.
Теперь рассмотрим вторую задачу.
Площадь прямоугольника 126 см2, а периметр – 46 см. Найти его длину и ширину.
Находим полупериметр, то есть, сумму двух сторон прямоугольника.
({color{red} a+b=46:2=23}) см.
Найдем максимально возможную площадь прямоугольника при данном значении суммы двух его сторон, то есть, полупериметра. Так как полупериметр – нечетное число, значит, нам нужен такой прямоугольник, разница между значениями ширины и длины которого в натуральных числах минимальна, то есть, единица. Это прямоугольник со сторонами 11 и 12, т.к. ({color{red} 23=11+12}).
Площадь такого прямоугольника равна:
({color{red}S_{2}=11cdot 12=132}) см2.
Разница между полученной площадью и заданной по условию задачи составляет:
({color{red}S_{2}-S=132-126=6}) см2.
6 см2 – это площадь прямоугольника со сторонами 2 и 3 см. Чтобы уменьшить площадь нашего прямоугольника со сторонами 11 см и 12 см, нужно увеличить разницу между значениями этих сторон, а именно, уменьшить его короткую сторону, то есть, ширину. При этом длину также нужно увеличить на это же число, чтобы сохранить значение периметра.
Для этого ширину 11 мы уменьшаем на одноименное значение, то есть, тоже на ширину прямоугольника с площадью 6 см2, а именно, на 2.
Кстати, подумайте и напишите в комментарии к этой статье, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью (например, в этой задаче как прямоугольник 2 на 3, а не 1 на 6, а в первой – как квадрат 2 на 2, а не прямоугольник 1 на 4), и почему ширину уменьшаем именно на ширину (в этой задаче 11 – 2, а не 11 – 3).
Находим ширину искомого прямоугольника:
({color{red} a=11-2=9}) см.
Длину нужно увеличить также на это число, чтобы не изменился периметр прямоугольника:
({color{red} b=12+2=14}) см.
Проведем проверку:
({color{red} P=2cdot (9+14)=2cdot 23=46}) см.
({color{red}S=9cdot 14=126}) см2.
И эта задача решена тоже верно.
На этом все. Не забудьте написать в комментарии ответы на вопросы, почему мы рассматриваем разницу в площадях именно как прямоугольник с максимальной площадью, и почему ширину уменьшаем именно на ширину.
Вам также пригодится:
Лучший ответ
Лариса Манушкина
Гуру
(3274)
11 лет назад
Обозначим стороны прямоугольника х и у.
Тогда, периметр равен 2(х+у) =22
А площадь соответственно ху=30, т. е. х=30/у
Подставляем значение х в уравнение 2(х+у) =22.
Получаем 2(30/у+у) =22
30/у+у=11
Умножив обе части уравнения на у, получаем
30+у^2=11у
у^2-11у+30=0
у1+у2=11
у1*у2=30
У уравнения 2 корня у=5; у=6
Ответ стороны прямоугольника равны 5 и 6 см соответственно.
Андрей ОболонскийУченик (243)
2 года назад
А почему же x=30y просто я недопонял
DoctoR R@Ve№Мастер (1383)
11 месяцев назад
А куда Х слинял?
Остальные ответы
Полина Т.
Просветленный
(27763)
11 лет назад
сумма сторон равна 11см (22/2), а их произведение 30см, следовательно стороны равны 6см и 5см. (Может можно ещё каким-то способом, но я знаю только этот)
Scarabey
Искусственный Интеллект
(110810)
11 лет назад
просто, пусть сторона прямоугольника х, тогда вторая будет (22-2х) /2. площадь прямоугольника (22-2х) /2*х = 30
11х-x^2=30
x^2-11x+30 = 0
дальше решай сам
Аким Рамазанов
Ученик
(103)
7 лет назад
а если площадь40 см2 периметр 26см
Capitan NemoЗнаток (276)
3 года назад
алгоритм один и тот же, просто значения разные : )
Анна
Ученик
(148)
6 лет назад
кто бы еще дал окончательное решение 🙁
Kamronbek Kamoliddinovich
Ученик
(101)
2 года назад
как найти стороны прямоугольника если известно периметр 390 см
Катя Смирнова
Ученик
(133)
2 года назад
Площадь 72.периметр38 помогите
|
Площадь – 56 квадратных см. Периметр – 30 см.
Сторона А=7, сторона В=8 S=AxB P=2A+2B S=56 P=30 автор вопроса выбрал этот ответ лучшим Можно попробовать решить данную задачу, составив систему уравнений. Периметр прямоугольника равен: p=2a+2b; Площадь прямоугольника равна: s=a*b; Так как мы знаем периметр и площадь, то сразу подставляем числа: 30=2a+2b; 56=a*b; Выражаем b через a во втором уравнении: b=56/a; И подставляем 56/a вместо b в первое уравнение: 30=2a+2(56/a); 15=a+56/a; Домножаем обе части на a: 15a=a²+56; Получаем квадратное уравнение: a²-15a+56=0; Находим корни этого квадратного уравнения: (15±√(15²-4*1*56))/2*1 = (15±√(225-224))/2 = (15±√1)/2 = (15±1)/2 Получилось, что корни этого уравнения: a1=(15+1)/2=16/2=8; a2=(15-1)/2=14/2=7; Получается, что у нас 2 возможных варианта прямоугольников. Вспомним, что мы выразили: b=56/a; Отсюда находим возможные b: b1=56/a1=56/8=7; b2=56/a2=56/7=8; Как оказалось эти два разных прямоугольника – это один и тот же, просто достигнуть периметра в 30 при площади в 56 можно: Если a=7 и b=8. Либо наоборот: a=8 и b=7. То есть в сущности у нас один и тот же прямоугольник, просто в одном варианте вертикальная сторона больше горизонтальной, а в другом наоборот – горизонтальная больше вертикальной. Ответ: одна сторона 7 сантиметров, а вторая 8 сантиметров.
Oleg74 9 лет назад Если периметр прямоугольника Р = 30 см, а его площадь S = 56 см, то его стороны будут равны : а – одна сторона, в – другая сторона прямоугольника. S = а * в P = 2а + 2в Решив эту систему, приходим к тому, что сторона а будет равна 7 см, а сторона в будет равна 8 см. а = 7 см в = 8 см. Чтобы решить поставленную задачу, нужно составить систему уравнений и решить ее S = а*b P = 2(а+b) получим квадратное уравнение, которое легко решается, если подставить в него значения периметра и площади
Дискриминант равен 1 и уравнение имеет два корня 7 и 8, следовательно одна из сторон равна 7 см, другая 8 см или наоборот. Я специально выписал здесь дискриминант, так как по нему очень хорошо ориентироваться если в условии задачи на нахождение сторон прямоугольника значение периметра и площади заданы так, что этот дискриминант больше ноля, тогда мы имеем прямоугольник; если дискриминант равен нолю – тогда имеем квадрат (P=30, S=56,25, квадрат со стороной 7,5); если дискриминант меньше ноля, то тогда такой прямоугольник не существует (P=20, S=56 – решения нет)
Galina7v7 7 лет назад Дано: S = 56 смР = 30 смСтороны=?Решение:Пусть стороны прямоугольника a и b. Тогда: площадь S = a * b , периметр Р=2*(a + b), Получим систему уравнений: {a*b=56 ? {ab=56 {2(a+b)=30, {a+b=15 ,выражая b через а получим квадратное уравнение: b=15-a, a^2 -15a +56 =0 ,решая которое ,получим : a1=7, a2=8, b1=8, b2=7. То есть стороны прямоугольника: a=7,b=8 ,или наоборот:a=8,b=7.
Zolotynka 7 лет назад Нашла еще такое решение, Известно, что периметр прямоугольника 30 а площадь 56, далее: периметр = 2*(длина + ширина) или 2L + 2W площадь= длина * ширина или L * W 2L + 2W = 30 (делим обе части на 2) L + W = 15 L * W = 56 L * (15 – L) = 56 Честно говоря, не совсем поняла решение, но думаю, тот, кто не совсем подзабыл математику, разберется.
Azamatik 7 лет назад Вспоминаем школьную геометрию: Периметр прямоугольника – это будет сумма длин всех сторон, а площадь прямоугольника – это уже произведение двух смежных его сторон (длину на ширину). В данном случае нам известны и Площадь и Периметр прямоугольника. Они равны 56 см^2 и 30 см соответственно. Итак, решение: S – площадь = а x b; 56 = a x b; Р – периметр = а + b + a + b = 2a + 2b; 30 = 2 (а + b); 15 = a + b; a = 15 – b; Делаем подставление: 56 = (15 – b) x b; 56 = 15 b – b^2; b^2 – 15b + 56 = 0. Получили квадратное уравнение, решая которое получаем: b1 = 8, b2 = 7. Находим и другую сторону прямоугольника: a1 = 15 – 8 = 7; a2 = 15 – 7 = 8. Ответ: стороны прямоугольника равны 8 и 7 см или же 7 и 8 см.
Зная формулы периметра прямоугольника и его площади, стороны ищутся в виде решения системы двух уравнений. Для начала выражаем значение одной стороны через другую и например площадь.Это выглядит так А=S/В=56/В Затем подставляем это выражение вместо буквы А в уравнении для периметра: Р=2(56/В + В)=30 Получаем что 56/В+В=15 В этом уравнении даже решать его не надо – любому человеку знакомому с таблицей умножения сразу видно, что 56 это произведение 7 и 8, а поскольку и сумма этих цифр как раз 15, то они и есть нужные нам значения сторон прямоугольника.
Хеленочка 8 лет назад Обозначим одну сторону буквой Х, другую – буквой Y. Площадь прямоугольника вычисляется умножением длин сторон, следовательно, мы можем составить первое уравнение: Х*Y=56 Периметр – это сумма длин сторон, следовательно, второе уравнение такое: 2Х+2Y=30 Получаем систему двух уравнений. По первому уравнению выделяем Х: Х=56:Y, подставляем это во второе уравнение: 2*56:Y+2Y=30 Отсюда уже легко найти значение Y: Y=7, тогда Х=8. Lilechka 9 лет назад Периметр 30, площадь 56. Назовем стороны прямоугольника а и с. Тогда можем составить такие уравнения: (а+c)х2=30 ахс=56 Далее решаем систему уравнений и находим, что стороны прямоугольника составляют 7 и 8 см.
moreljuba 7 лет назад Итак, для начала рассмотрим формулы для нахождения площади и периметра: 1) S = a * b = 56 см2; 2) Р = 2а + 2b = 30 см. Ведь мы знаем, что прямоугольник имеет по две одинаковых стороны. Таким образом нам требуется решить систему из двух уравнений: a * b = 56 2а + 2b = 30 Отсюда получаем, что одна сторона равна 7, а другая 8. Знаете ответ? |
Установить Длина сторон прямоугольника на мобильный
Найти длину стороны прямоугольника
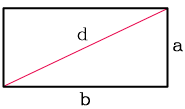
зная диагональ и сторону
|
||
| Диагональ прямоугольника d | ||
| Сторона прямоугольника a | ||
|
|
||
| Сторона прямоугольника b |
Найти длину стороны прямоугольника
зная периметр и сторону
|
||
| Периметр прямоугольника P | ||
| Сторона прямоугольника a | ||
| Сторона прямоугольника b |
Найти длину стороны прямоугольника
зная площадь и сторону
|
||
| Площадь прямоугольника S | ||
| Сторона прямоугольника a | ||
| Сторона прямоугольника b |
Скачать калькулятор
Рейтинг: 3.1 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Сторона квадрата |
| Стороны ромба | Стороны параллелограмма | Ребро куба | Боковое ребро параллелепипеда |
Как найти стороны прямоугольника, если известен его периметр в см и одна сторона больше другой на i см?
i = a — b ⇒ a = i + b
P = 2(a + b) ⇒ a = P : 2 — b
i + b = P : 2 — b ⇒ b = ( 0,5 P — i ) : 2 = 0,25 P — 0,5 i
a = i + 0,25 P — 0,5 i = 0,25 P + 0,5 i
Итого площадь прямоугольника можно найти по формуле:
a = 0,25 P + 0,5 i
b = 0,25 P — 0,5 i
P — периметр прямоугольника в см (сантиметрах);
a — длина одной из сторон прямоугольника в см (сантиметрах);
b — длина другой стороны прямоугольника в см (сантиметрах);
i — на сколько см (сантиметров) длина стороны a больше длины стороны b.
Например:
Периметр прямоугольника равен 44 см, одна сторона больше другой на 2 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 44 + 0,5 • 2 = 12 см
b = 0,25 P — 0,5 i = 0,25 • 44 — 0,5 • 2 = 10 см
Периметр прямоугольника равен 58 см, одна сторона больше другой на 5 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 58 + 0,5 • 5 = 17 см
b = 0,25 P — 0,5 i = 0,25 • 58 — 0,5 • 5 = 12 см
Периметр прямоугольника равен 18 см, одна сторона больше другой на 3 см. Найдите стороны прямоугольника.
Краткое решение:
a = 0,25 P + 0,5 i = 0,25 • 18 + 0,5 • 3 = 6 см
b = 0,25 P — 0,5 i = 0,25 • 18 — 0,5 • 3 = 3 см