Как найти длину световой волны дифракционной решетки

Тема: Определение длины волны светового излучения с помощью дифракционной решётки

Цель: Познакомиться на опыте с явлением многолучевой интерференции световых волн. Используя решётку с известным расстоянием между штрихами измерить длину волны светового излучения.

Оборудование:

1. Штатив.
2. Дифракционная решётка 100 штрихов на мм.
3. Измерительная лента.

Теория

Дифракция волн – огибание волнами различных препятствий (неоднородностей).

Препятствия нарушают прямолинейность распространения фронта волны.

Дифракция волн свойственна всякому волновому движению; проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней, однако проявляется всегда. Для увеличения яркости дифракционной картины нужно пропускать свет через несколько параллельных щелей. В этом случае кроме явления дифракции будет происходить ещё и явление интерференции, т.к. лучи, идущие от всех лучей, оказываются когерентными.

Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.

Дифракционная решетка – оптический прибор, представляющий собой большое число параллельных и очень близко расположенных узких щелей, которые пропускают или отражают свет.

Дифракционные решетки с различным числом щелей на 1 мм:

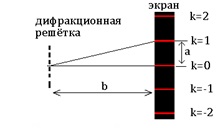
Параллельный пучок света с длиной волны λ, проходя через дифракционную решётку, вследствие дифракции за решёткой, распространяется по всевозможным направлениям и интерферирует. На экране, установленном на пути интерферирующего света, можно наблюдать интерференционную картину:

Максимумы света наблюдаются в точках экрана, для которых выполняется условие максимума:

   

Условие максимума: на разности хода волн укладывается четное число полуволн (целое число длин волн): Δ=k·λ,  (1)

где  Δ=АС – разность хода волн; λ – длина световой волны; k – номер максимума.

Центральный максимум (в точке О) называют нулевым; для него Δ=0. Слева и справа от него располагаются максимумы высших порядков.

Условие возникновения максимума можно записать иначе:

d·sinφ=k·λ

где k=0; ± 1; ± 2; ± 3…

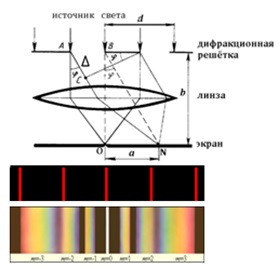
Здесь d – период дифракционной решётки в мм, φ – угол, под которым виден световой максимум k-го порядка в точке N на расстоянии а от нулевого максимума, а λ – длина волны.

Так как углы дифракции малы, то для них можно принять: sinφ ≈ tgφ, а tgφ=a/b.

Поэтому: 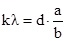 , и искомая длина световой волны равна  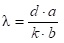(2)

В данной работе формулу (2) используют для вычисления длины световой волны.

Из условия максимума следует sinφ=(k·λ)/d .

   Пусть k=1, тогда sinφ_кр=λ_кр/d и sinφ_ф=λ_ф/d.

   Известно, что λ_кр>λ_ф , следовательно sinφ_кр>sinφ_ф. Т.к. y= sinφ_ф – функция возрастающая, то φ_кр>φ_ф

   Поэтому фиолетовый цвет в дифракционном спектре располагается ближе к центру.

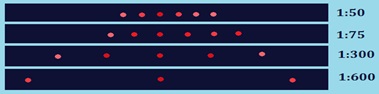
Между максимумами расположены минимумы освещенности. Чем больше общее число щелей и чем ближе друг к другу они расположены, тем более широкими промежутками разделены максимумы.

Картина дифракции лазерного излучения красно цвета на решётках с различным числом щелей на 1 мм:

Ход работы

1. Перенести рисунок в тетрадь.

 

1. Подготовить таблицу для записи результатов измерений:

Порядок спектра, цвет k	Постоянная  решётки, d мм	Расстояние от решётки до экрана, b мм	Расстояние от нулевого максимума до максимума k-порядка а мм	Длина волны, нм	Средняя длина волны нм	Относительная погрешность измерения δ %
1-ый, красный	1:100=0,001
2-ой, красный	1:100=0,001
1-ый, фиолетовый	1:100=0,001
2-ой, фиолетовый	1:100=0,001

1. Укрепить в штативе линейку с экраном и закрепить на направляющей линейки дифракционную решётку.
2. Установить расстояние от решётки до экрана 40 см (b).Результат записать в таблицу.
3. Смотря через дифракционную решётку, направить прибор на источник света. Пронаблюдать спектр:

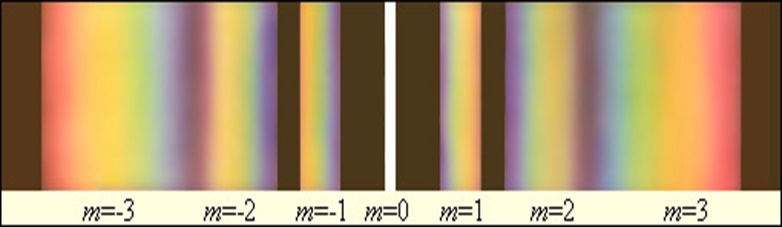
Измерить на экране расстояние а между нулевым максимумом и максимумом 1-го  порядка для красного света.  Результат записать в таблицу.

1. Измерить на экране расстояние а между нулевым максимумом и максимумом 2-го порядка для красного света. Результат записать в таблицу.
2. Повторить опыт, измерив на экране расстояние а между нулевым максимумом и максимумом 1-го и 2-го порядка для фиолетового света. Результат записать в таблицу.
3. По формуле 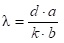  рассчитать длину волны излучения.
4. Найти среднее значение длины волны светового излучения для красного λкр ср=( λкр1+λкр2)/2
    и фиолетового света   .λф ср=( λф1+λф2)/2 

1. Зная истинное значение длины волны лазерного излучения , рассчитать относительную погрешность измерений:

δ=( λкр ср – λкр табл)/λкр табл *100%       и δ=( λф ср – λф табл)/λф табл *100%

Диапазон длин волн, нм

Красный 625—740 нм (λ_{кр табл}= 680 нм)

Фиолетовый 380—440 нм (λ_{ф табл} = 410 нм)

1. Записать вывод по результатам выполненной работы.
2. Ответить письменно на контрольные вопросы.

Контрольные вопросы

1. Какие волны называются когерентными?
2. В чём заключается явление дифракции?
3. Какие свойства света подтверждает дифракция света?
4. При каких условиях наблюдается дифракция света?
5. Как образуется дифракционный спектр?
6. Почему максимумы располагаются как слева, так и справа от нулевого максимума?
7. В чём разница в дифракционных картинах решёток с 50 и 300 штрихами на одном миллиметре?

1. Определение длины световой волны при помощи дифракционной решетки

1. определить
   длину световой волны при помощи
   дифракционной решетки

1. лабораторная
   установка с дифракционной решеткой,
   источник света

Краткая теория

Дифракцией называется совокупность
явлений, наблюдаемых при распространении
света в среде с резкими неоднородностями
(например, вблизи границ непрозрачных
или прозрачных тел, сквозь малые отверстия
и т.п.) и связанных с отклонениями от
законов геометрической оптики. Дифракция,
в частности, приводит к огибанию волнами
препятствий, соизмеримых с длиной волны,
и проникновению света в область
геометрической тени.

Между
интерференцией и дифракцией нет
существенного физического различия.
Оба явления заключаются в перераспределении
светового потока в результате суперпозиции
волн. Перераспределение интенсивности,
возникающее в результате суперпозиции
волн, возбуждаемых конечным числом
дискретных когерентных источников,
принято называть интерференцией
волн. Перераспределение интенсивности,
возникающее в результате суперпозиции
волн, возбуждаемых когерентными
источниками, расположенными непрерывно,
принято называть дифракцией
света.

Различают
два вида дифракции. Если источник света
S
и точка наблюдения Р
расположены от препятствия настолько
далеко, что лучи, падающие на препятствие,
и лучи, идущие в точку Р,
образуют практически параллельные
пучки, говорят о дифракции
в параллельных лучах
или о дифракции
Фраунгофера.
В противном случае говорят о дифракции
Френеля.

Проникновение
световых волн в область геометрической
тени может быть объяснено с помощью
принципа Гюйгенса, согласно которому
каждая точка, до которой доходит волновое
движение, служит центром вторичных волн
(в изотропной и однородной среде они
будут сферическими). Огибающая этих
волн дает положение фронта волны в
следующий момент времени.

Однако этот
принцип не дает сведений об амплитуде,
а, следовательно, и об интенсивности
волн, распространяющихся в различных
направлениях. Френель дополнил принцип
Гюйгенса представлением интерференции
вторичных волн. Учет амплитуд и фаз
вторичных волн позволяет найти амплитуду
результирующей волны в любой точке
пространства. Развитый таким способом
принцип Гюйгенса получил название
принципа Гюйгенса – Френеля.

Согласно
принципу Гюйгенса – Френеля каждый
элемент волновой поверхности служит
источником вторичной сферической волны,
амплитуда которой пропорциональна
величине элемента dS.
Амплитуда сферической волны убывает с
расстояниемrот источника
по закону.
Следовательно, от каждого участкаdSволновой поверхности в точкуР,
лежащую перед этой поверхностью, приходит
колебание

где – фаза колебаний в месте расположения
волновой поверхностиS,

k– волновое число,

а₀– определяется амплитудой
светового колебания в том месте, где
находитсяdS.

Коэффициент
пропорциональности Кзависит от
угламежду нормальюnк
площадкеdSи направлением
отdSк точкеР. Приэтот коэффициент максимален, прион обращается в нуль.

Результирующее
колебание в точке Рпредставляет
собой суперпозицию колебаний, взятых
для всей волновой поверхностиS:

.

Эта
формула является аналитическим выражением
принципа Гюйгенса – Френеля.

Для наблюдения
дифракционной картины в данной работе
используется дифракционная решетка –
совокупность большого числа одинаковых,
отстоящих друг от друга на одно и то же
расстояние щелей. Дифракционная решетка
имеет две характеристики, которые
связаны между собой следующим соотношением:

,

где N– число штрихов на 1мм,

С– постоянная
(период) решетки.

Постоянная
решетки равна сумме ширины прозрачного
промежутка аи непрозрачного штриха
в:С=а+в.

Выясним характер
дифракционной картины, получающейся
на экране при нормальном падении на
решетку плоской световой волны (рис.
22.1). Из рисунка 22.1 видно, что разность
хода от соседних щелей (отрезок А₁К),
где– угол отклонения луча от первоначального
направления. Следовательно, в точках,
в которых выполняется условие

,

колебания взаимно усиливают
друг друга, если m–
четное, и ослабляют, еслиm– нечетное (– длина волны падающего излучения).

Р

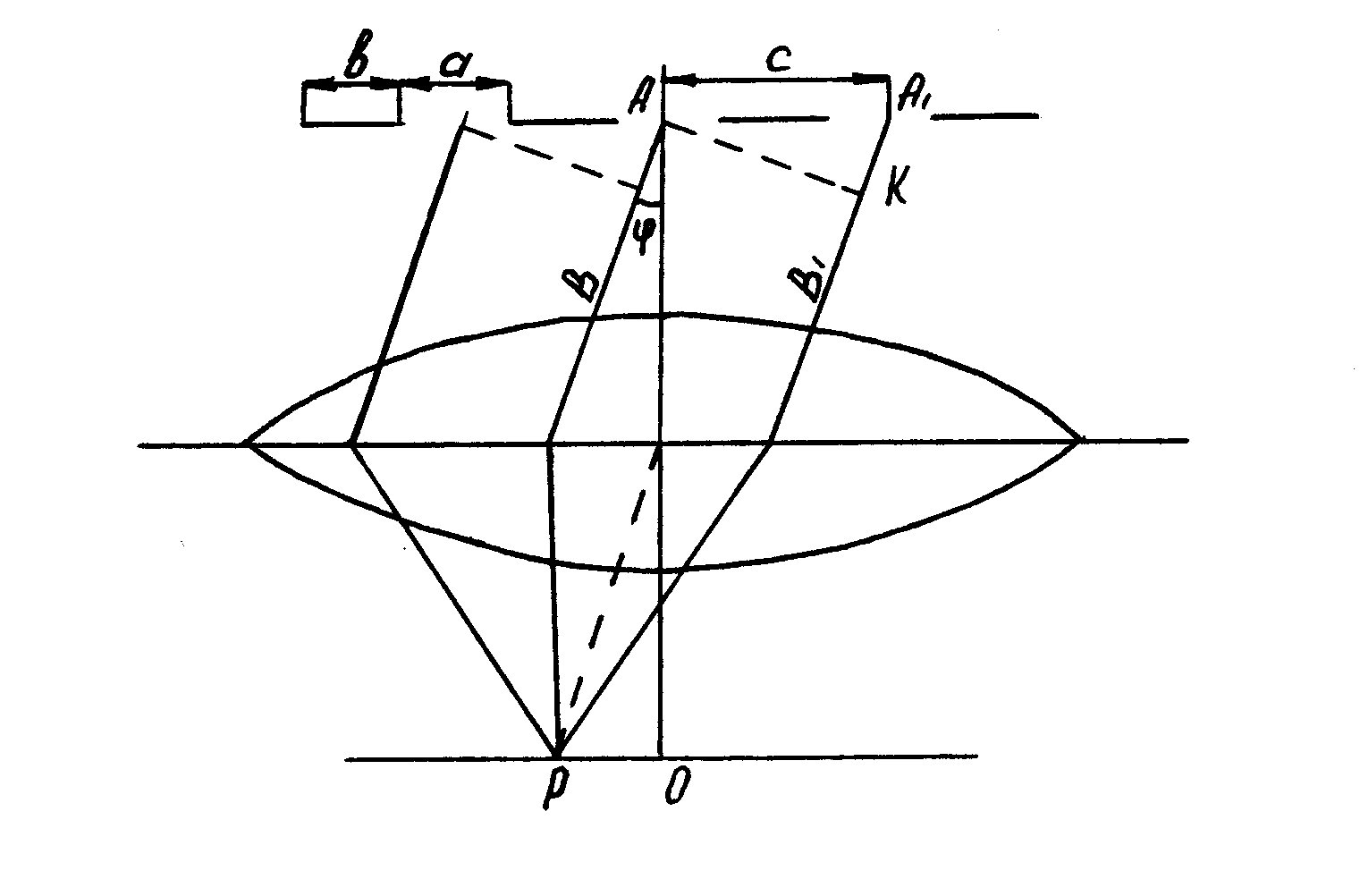
Рис.
22.1 – Схема дифракции световых волн

езультирующее колебание в точкеРдифракционной картины, положение которой
определяется углом
,
представляет собой суммуNколебаний с одинаковой амплитудой,
сдвинутых друг относительно друга по
фазе на одну и ту же величину
.
Интенсивность при этих условиях равна

Из рисунка 22.1
видно, что разность хода от соседних
щелей равна
.
Следовательно, разность фаз

,

где длина волны в данной среде.

Окончательное
выражение для интенсивности имеет:

.

Первый
множитель обращается в нуль в точках,
для которых

(22.1)

В этих точках
интенсивность, создаваемая каждой из
щелей в отдельности, равна нулю. Это
условие определяет положение минимумов
интенсивности.

Второй множитель
принимает значение
в точках, удовлетворяющих условию

(22.2)

Это условие
определяет положение максимумов
интенсивности, называемых главными.
Числоmдает порядок
главного максимума. Максимум нулевого
порядка только один, остальных по два.

Кроме
минимумов, определяемых условием (22.1),
в промежутках между соседними главными
максимумами имеется по (N–1)
добавочных минимума. Эти минимумы
возникают в том направлении, для которых
колебания от соседних щелей погашают
друг друга. Направлениядобавочных
минимумов определяется условием:

,

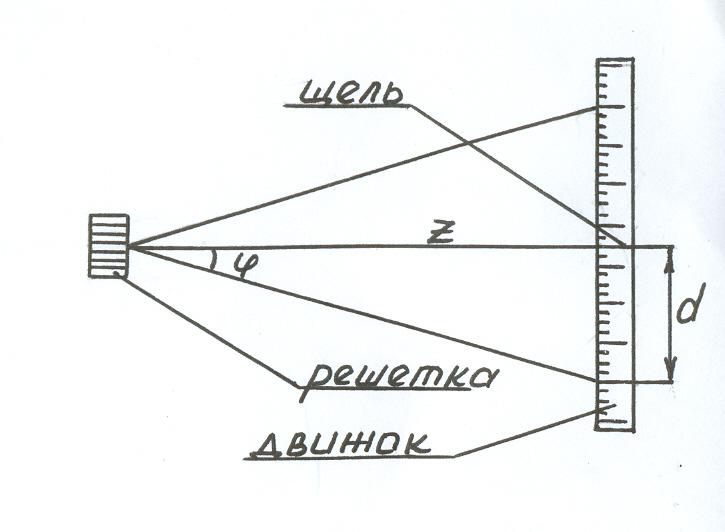
Рис. 22.2 – Схема
экспериментальной установки

т.е.
принимает все целочисленные значения,
кроме 0,N, 2N,…
т.к. при этих значениях это условие
переходит в условие (22.2).

Из
условия, определяющего положение главных
максимумов (22.2), следует, что

.
(22.3)

Эта формула
лежит в основе способа определения
длины волны в данной работе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Простейшее измерительное устройство на рисунке ниже состоит из двух линеек, на одной из которых закреплена дифракционная решётка, а над второй возвышается узкая щель, например, из двух лезвий. Используются расстояния в миллиметрах от дифракционной решётки до линейки с щелью, и от щели (максимума нулевого порядка) до максимума первого порядка.

Нужно смотреть через дифракционную решётку на источник света с известной длиной волны: лазер (важно следить, чтобы свет лазера гарантированно не мог повредить глаза: снижать яркость узкой щелью, отражением, светорассеивателем) или пламя горелки, окрашенное в жёлтый цвет двумя линиями 588,995 и 589,5924 нм с помощью проволоки, покрытой раствором соли NaCl и внесённой в огонь. Также подойдёт турбо зажигалка с красным пламенем, дающим в спектре тонкую линию 670,78 нм. Скорее всего в ней используется пластина с веществом, содержащим литий. Если кто знает подобную информацию о зажигалке с зелёным пламенем, то напишите, пожалуйста, комментарий.

Период дифракционной решётки можно посчитать следующим образом:

589нм*204мм/20мм≈6000 нм

Этим же устройством можно определить длину волны света, зная период дифракционной решётки:

20*6000/204≈588 нм.

Существует и немного другой вариант устройства. Лазер светит через дифракционную решётку на линейку. В этом случае щель не нужна.

Им тоже можно определить характеристику дифракционной решётки и света, но только с помощью лазеров.

Период решётки: 780нм*250мм/32,5мм=6000 нм

Длина волны: 32,5мм*6000нм/250мм=780 нм

Я использовал дифракционную решётку из насадки “Звёздное небо”, которая шла в комплекте с лазерной указкой. Там две решётки. Насадку нужно разобрать и вытащить одна решётку. Дифракционная решётка из CD даёт ошибку в 100 нм и не подходит.

Готовую фотографию спектра минимум с двумя известными линиями можно сопоставить в Photoshop со шкалой, чтобы узнать длины волн неизвестных линий.

Создаём чистый лист, вставляем на него шкалу и изображение, на котором есть неизвестные длины волн. Для сопоставления известных длин волн со шкалой, изменяем масштаб фотографии таким образом: нажимаем “Редактирование”, “Трансформирование”, “Масштабирование”; нажимаем кнопку “Сохраняет пропорции” и меняем числовые значения вверху, указанные в %. После сопоставления, неизвестные длины волн автоматически займут правильные положения на шкале. Должно получится примерно следующее:

Известные линии спектров газоразрядных ламп есть в ГОСТ Р 55703-2013. Некоторые спектры в виде графиков и в виде фотографий.

Можно использовать и математический метод. Например, нужно узнать длину волны лазера с фотографии выше. Открываем её в Photoshop CC. С помощью инструмента “Линейка” измеряем расстояние от линии натрия до линии лития. Оно равно 1223 п. Измеряем расстояние от натрия до лазера – 1104 п. Считаем таким образом: (670нм-589нм)/1223п*1104п+589нм=662 нм

Если у нас фотография с источником излучения, полученная простейшим спектроскопом, то неизвестную линию считаем так.

Узнаём линию 1064 нм. Измеряем расстояние от точки лазера до линии 802 нм. Будет 2876 п. От лазера до неизвестной линии – 3831 п. 802нм*3831п/2876п=1068 нм

Обновляемая тематическая подборка статей моего канала здесь.

Спасибо за то, что дочитали мою статью!

Если информация понравилась, ставьте лайк. Также буду рад комментариям!