Как найти длину свободного пробега молекул водорода

Как найти длину свободного пробега молекул водорода

Тема: Определить среднюю длину свободного пробега молекул водорода  (Прочитано 7185 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Определить среднюю длину свободного пробега молекул водорода при температуре t = 27 ºС и давлении р = 4 мкПа. Принять диаметр молекулы водорода d = 2,3∙10-10 м.

« Последнее редактирование: 17 Мая 2015, 15:05 от Сергей »


Записан

Решение.
Средняя длина свободного пробега молекулы определяется по формуле:

[ l=frac{1}{sqrt{2}cdot pi cdot {{d}^{2}}cdot n} (1). ]

n – концентрация молекул газа.
Концентрацию молекул газа определим по формуле:

[ p=ncdot kcdot T, n=frac{p}{kcdot T} (2). ]

   

k – постоянная Больцмана, k = 1,38∙10-23 Дж/К.
Подставим (2) в (1) определим длину свободного пробега молекулы газа водорода:

[ l=frac{kcdot T}{sqrt{2}cdot pi cdot {{d}^{2}}cdot p} (3). ]

Т = (273 + 27)К = 300 К. р = 4∙10-6 Па.
l = 4419,12 м.

« Последнее редактирование: 24 Мая 2015, 06:15 от alsak »


Записан

Источник

Меню

  • Главная
  • Заказ решений
  • Готовые решения
  • Статьи
  • Новости
  • Авторы

 Есть идеи?

Решения Чертовасайт решений Чертова А.Г. Воробьева А.А.

Поиск

Глава2. Молекулярная физика и термодинамика (§ 8-12) >> §10 Элементы статистической физики >> задача – 10.47


Условие:

Найти среднюю длину свободного пробега молекул водорода при давлении p=0,1 Па и температуре Т=100 К.

При клике на картинку откроется ее увеличенная версия в новой вкладке.

Решение задачи 10.47. Чертов А.Г. Воробьев А.А.

Не забываем поделиться записью!

Последние статьи

  • Подходы к решению задач по физике
  • Что такое физика и какие задачи и вопросы она решает?
  • Общие рекомендации по решению статистических задач
  • Он-лаин или офф-лаин обучение? Что выбрать?
  • Изучение геометрии в восьмом классе без хлопот становится реальностью

Наши партнеры
Kwork.ru - услуги фрилансеров от 500 руб.

© 2012 Решения Чертова | Авторы Bandit & AJ Акции | Sitemap | FAQ&ask

Kwork.ru - услуги фрилансеров от 500 руб.

Источник

Страница 7 из 12

5.121. Найти среднюю длину свободного пробега ? атомов гелия, если известно, что плотность гелия p = 0,021 кг/м3.

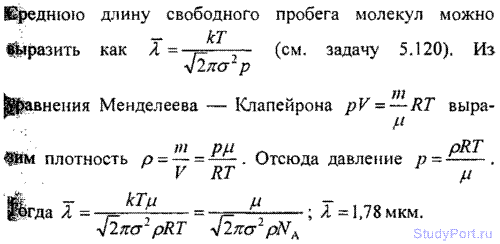
5.122. Найти среднюю длину свободного пробега ? молекул водорода при давлении p = 0,133 Па и температуре t = 50° С.

5.123. При некотором давлении и температуре t = 0°С средняя длина свободного пробега молекул кислорода ? = 95 нм. Найти среднее число столкновений z в единицу времени молекул кислорода, если при той же температуре давление кислорода уменьшить в 100 раз.

5.124. При некоторых условиях средняя длина свободного пробега молекул газа ?=160нм; средняя арифметическая скорость его молекул v = 1,95 км/с. Найти среднее число столкновений z в единицу времени молекул этого газа, если при той же температуре давление газа уменьшить в 1,27 раза.

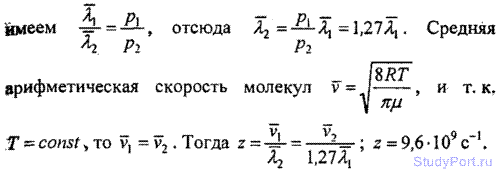
5.125. В сосуде объем V = 100см3 находится масса m = 0,5 г

азота. Найти среднюю длину свободного пробега ? молекул азота.

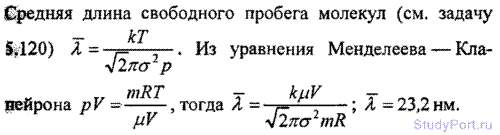
5.126. В сосуде находится углекислый газ, плотность которого p = 1,7 кг/м3. Средняя длина свободного пробега его

молекул ? = 79 нм. Найти диаметр а молекул углекислого газа.

5.127. Найти среднее время г между двумя последовательными столкновениями молекул азота при давлении p = 133 Г температуре t = 10° С.

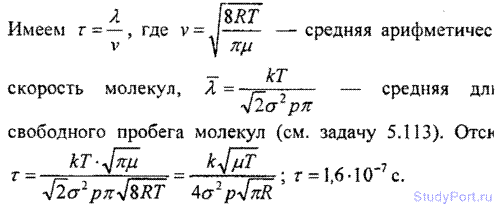
5.128. Сосуд с воздухом откачан до давления p = 1,33 • 10-1 Па. Найти плотность p воздуха в сосуде, число молекул n в единице объема сосуда и среднюю для свободного пробега ? молекул. Диаметр молекул воздуха ? = 0,3 нм. Молярная масса воздуха u = 0,029 кг/моль Температура воздуха t = 17° С.

5.129. Какое предельное число n молекул газа должно находиться в единице объема сферического сосуда, чтобы молекулы не сталкивались друг с другом? Диаметр молекул ? = 0,3 нм, диаметр сосуда D = 15 см.

5.130. Какое давление p надо создать внутри сферического

сосуда, чтобы молекулы не сталкивались друг с другом, если диаметр сосуда: a) D = 1cm; б) D = 10см; в) D = 100см? Диаметр молекул газа ? = 0,3 нм.

5.131. Расстояние между катодом и анодом в разрядной трубке d = 15 см. Какое давление p надо создать в разрядной трубке, чтобы электроны не сталкивались с молекулами воздуха на. пути от катода к аноду? Температура воздуха t = 27° С. Диаметр молекул воздуха ? = 0,3 нм. Средняя длина свободного пробега электрона в газе приблизительно в 5,7 раза больше средней длины свободного пробега молекул самого газа.

5.132. В сферической колбе объемом V = 1л находится азот. При какой плотности p азота средняя длина свободного пробега молекул азота больше размеров сосуда?

5.133. Найти среднее число столкновений z в единицу времени молекул некоторого газа, если средняя длина

свободного пробега ? =5 мкм, а средняя квадратичная скорость его молекул sqr(v2) = 500 м/с.

5.134. Найти коэффициент диффузии D водорода при нормальных условиях, если средняя длина свободного пробега ? = 0,16 мкм.

5.135. Найти коэффициент диффузии D гелия при нормальных условиях.

5.136. Построить график зависимости коэффициента диффузии D водорода от температуры Т в интервале 100 < Т < 600 К через каждые 100 К при p = const = 100 кПа.

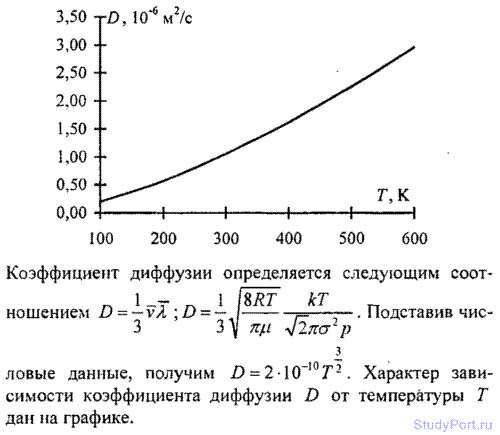
5.137. Найти массу m азота, прошедшего вследствие диффузии через площадку S = 0,01м2 за время t = 10 с. если градиент плоскости в направлении, перпендикулярном к площадке, dp/ dх = 1,26 кг/м4. Температура азота t = 27° С. Средняя

длина свободного пробега молекул азота ? = 10 мкм.

5.138. При каком давлении p отношение вязкости некоторого газа к коэффициенту его диффузии n/D = 0,3 кг/м3, а средняя квадратичная скорость его молекул sqr(v2) = 632 м/с?

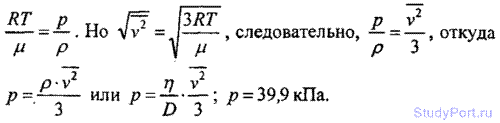
5.139. Найти среднюю длину свободного пробега Я молекул гелия при давлении p = 101,3 кПа и температуре t = 0°C, если

вязкость гелия n = 13мкПа*с.

5.140. Найти вязкость n азота при нормальных условиях,

если коэффициент диффузии для него D = 1,42 • 10-5 м2/с. Найти диаметр молекулы кислорода, если при температуре вязкость кислорода.

Источник

[03.04.2014 19:31]

Решение 6041:

Найти среднюю длину свободного пробега молекул водорода при давлен

…
Подробнее смотрите ниже

Номер задачи на нашем сайте: 6041

ГДЗ из решебника:

Тема:

Глава 2. Молекулярная физика и термодинамика
§ 10. Элементы статистической физики

Нашли ошибку? Сообщите в комментариях (внизу страницы)

Раздел: Физика

Полное условие:

10.47. Найти среднюю длину свободного пробега молекул водорода при давлении p=0,1 Па и температуре T=100 К.

Решение, ответ задачи 6041 из ГДЗ и решебников:

Этот учебный материал представлен 1 способом:

Для просмотра в натуральную величину нажмите на картинку

Найти среднюю длину свободного пробега молекул водорода при давлен..., Задача 6041, Физика

Идея нашего сайта – развиваться в направлении помощи ученикам школ и студентам.
Мы размещаем задачи и решения к ним. Новые задачи, которые недавно добавляются на наш сайт,
временно могут не содержать решения, но очень скоро решение появится, т.к. администраторы следят
за этим. И если сегодня вы попали на наш сайт и не нашли решения, то
завтра уже к этой задаче может появится решение, а также и ко многим другим задачам. основной поток посетителей к нам – это
из поисковых систем при наборе запроса, содержащего условие задачи

Счетчики: 8420
| Добавил: Admin
Добавить комментарий

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

|

Вход

]
Источник

Длина свободного пробега молекулы — это среднее расстояние lambda , которое пролетает частица за время между двумя последовательными столкновениями.[1]

Для каждой молекулы это расстояние различно, поэтому в кинетической теории газов под длиной свободного пробега обычно подразумевается[2] средняя длина свободного пробега <lambda >, которая является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.

Теория рассеяния[править | править код]

Слой мишени

Представим поток частиц, проходящих через мишень размером {displaystyle Ltimes L}, и рассмотрим бесконечно тонкий слой этой мишени (см. рисунок).[3] Красным здесь обозначены атомы, с которыми частицы падающего пучка могут столкнуться. Значение длины свободного пробега будет зависеть от характеристик этой системы. Если все частицы мишени покоятся, то выражение для длины свободного пробега будет выглядеть как:

{displaystyle ell =(sigma n)^{-1},}

где n — количество частиц мишени в единице объёма, а σ — эффективное сечение.

Площадь такого слоя L2, объём L2 dx, и тогда количество неподвижных атомов в нём n L2 dx. Вероятность dP рассеяния этим слоем одной частицы равна отношению части площади сечения, «перекрываемой» всеми рассеивающими частицами, ко всей площади сечения:

{displaystyle dP={frac {sigma nL^{2},dx}{L^{2}}}=nsigma ,dx,} где σ — площадь, или, более точно, сечение рассеяния одного атома.

Тогда уменьшение dI интенсивности потока будет равно начальной интенсивности, умноженной на вероятность рассеяния частицы внутри мишени:

{displaystyle dI=-Insigma ,dx.}

Получаем дифференциальное уравнение

{displaystyle {frac {dI}{dx}}=-Insigma =-{frac {I}{ell }},}

решение которого известно как закон закон Бугера[4] и имеет вид {displaystyle I=I_{0}e^{-x/ell }}, где x — расстояние, пройденное пучком, I0 — интенсивность пучка до того, как он попал в мишень, а ℓ называется средней длиной свободного пробега, потому что она равна среднему расстоянию, пройденному частицей пучка до остановки. Чтобы убедиться в этом, обратим внимание, что вероятность того, что частица будет рассеяна в слое от x до x + dx, равна

{displaystyle dP(x)={frac {I(x)-I(x+dx)}{I_{0}}}={frac {1}{ell }}e^{-x/ell }dx.}

И таким образом, среднее значение x будет равно

{displaystyle langle xrangle =int _{0}^{infty }xdP(x)=int _{0}^{infty }{frac {x}{ell }}e^{-x/ell },dx=ell .}

Отношение части частиц, которые не рассеялись мишенью, к количеству, падающему на её поверхность, называется коэффициентом пропускания {displaystyle T=I/I_{0}=e^{-x/ell }}, где x = dx — толщина мишени

Кинетическая теория[править | править код]

В кинетической теории газов длина свободного пробега частицы (например, молекулы) — это среднее расстояние, которое проходит частица за время между столкновениями с другими движущимися частицами. В приведенном выше выводе предполагалось, что частицы-мишени находятся в состоянии покоя, поэтому формула {displaystyle ell =(nsigma )^{-1}}, вообще говоря, справедлива только для падающих частиц со скоростями, высокими относительно скоростей совокупности таких же частиц со случайным расположением. В этом случае движения частиц мишени будут незначительны, а относительная скорость примерно равна скорости частицы.

Если же частица пучка является частью установившейся равновесной системы с идентичными частицами, то квадрат относительной скорости равен:

{displaystyle {overline {mathbf {v} _{rm {relative}}^{2}}}={overline {(mathbf {v} _{1}-mathbf {v} _{2})^{2}}}={overline {mathbf {v} _{1}^{2}+mathbf {v} _{2}^{2}-2mathbf {v} _{1}cdot mathbf {v} _{2}}}.}

В состоянии равновесия значения скоростей {displaystyle mathbf {v} _{1}} и {displaystyle mathbf {v} _{2}} случайны и независимы, поэтому {displaystyle {overline {mathbf {v} _{1}cdot mathbf {v} _{2}}}=0}, а относительная скорость равна

{displaystyle v_{rm {rel}}={sqrt {overline {mathbf {v} _{rm {relative}}^{2}}}}={sqrt {overline {mathbf {v} _{1}^{2}+mathbf {v} _{2}^{2}}}}={sqrt {2}}v.}

Это означает, что количество столкновений равно {sqrt {2}}, умноженному на количество неподвижных целей. Следовательно, применимо следующее соотношение:[5]

{displaystyle ell =({sqrt {2}},nsigma )^{-1}}

Из закона Менделеева-Клапейрона {displaystyle n=N/V=p/(k_{text{B}}T)} и с учётом {displaystyle sigma =pi (2r)^{2}=pi d^{2}} (эффективная площадь поперечного сечения для сферических частиц радиусом r) можно показать, что длина свободного пробега равна[6]

{displaystyle ell ={frac {k_{text{B}}T}{{sqrt {2}}pi d^{2}p}},} где kB — постоянная Больцмана.

На практике диаметр молекул газа не определён точно. Фактически, кинетический диаметр молекулы определяется через длину свободного пробега. Как правило, молекулы газа не ведут себя как твердые сферы, а скорее притягиваются друг к другу на больших расстояниях и отталкиваются друг от друга на меньших, что можно описать с помощью потенциала Леннарда-Джонса. Один из способов описать такие «мягкие» молекулы — использовать параметр σ Леннарда-Джонса в качестве диаметра. Другой способ — предположить, что газ в модели твердых сфер имеет ту же вязкость, что и рассматриваемый реальный газ. Это приводит к средней длине свободного пробега[7]

{displaystyle ell ={frac {mu }{p}}{sqrt {frac {pi k_{text{B}}T}{2m}}},}

где m — масса молекулы, а μ — вязкость. Это выражение можно удобно представить в следующем виде:

{displaystyle ell ={frac {mu }{p}}{sqrt {frac {pi R_{u}T}{2M}}},}

где {displaystyle R_{u}} — универсальная газовая постоянная, а M  — молекулярная масса. Эти разные определения диаметра молекулы могут привести к немного разным значениям длины свободного пробега.

Формула[править | править код]

lambda ={frac {1}{{sqrt {2}}sigma n}}, где sigma  — эффективное сечение молекулы, равное {displaystyle {pi d^{2}}} (d — эффективный диаметр молекулы), а n — концентрация молекул.

Примеры[править | править код]

В следующей таблице приведены типичные значения длины свободного пробега молекул воздуха при комнатной температуре для различных давлений.

Диапазон давления Давление, Па Давление, мм.рт.ст. Концентрация, молекул / см3 Концентрация, молекул / м3 Длина свободного пробега
Атмосферное давление 101300 759.8 2.7 × 1019 2.7 × 1025 68[8] нм
Низкий вакуум 30000 — 100 220 — 8×10−1 1019 — 1016 1025 — 1022 0.1 — 100 мкм
Средний вакуум 100 — 10−1 8×10−1 — 8×10−4 1016 — 1013 1022 — 1019 0.1 — 100 мм
Высокий вакуум 10−1 — 10−5 8×10−4 — 8×10−8 1013 — 109 1019 — 1015 10 см- 1 км
Сверхвысокий вакуум 10−5 — 10−10 8×10−8 — 8×10−13 109 — 104 1015 — 1010 1 km — 105 km
Экстремальный вакуум <10−10 <8×10−13 <104 <1010 >105 km

См. также[править | править код]

  • Вакуум
  • Рассеяние частиц
  • Физическая кинетика
  • Вязкость

Примечания[править | править код]

  1. ↑ Marion Brünglinghaus. Mean free path. Euronuclear.org.
  2. ↑ Алешкевич В.А. Курс общей физики. Молекулярная физика.. — М.: ФИЗМАТЛИТ, 2016. — С. 281—283. — 312 с. — ISBN 978-5-9221-1696-1.
  3. ↑ Chen, Frank F. Introduction to Plasma Physics and Controlled Fusion. — 1st. — Plenum Press, 1984. — P. 156. — ISBN 0-306-41332-9.
  4. ↑ Сивухин Д.В. Общий курс физики // Поглощение света и уширение спектральных линий. — Москва, 2005. — С. 582—583. — 792 с. — ISBN ISBN 5-9221-0228-1.
  5. ↑ S. Chapman and T. G. Cowling, The mathematical theory of non-uniform gases Архивная копия от 7 ноября 2020 на Wayback Machine, 3rd. edition, Cambridge University Press, 1990, ISBN 0-521-40844-X, p. 88.
  6. ↑ Mean Free Path, Molecular Collisions. Hyperphysics.phy-astr.gsu.edu. Дата обращения: 8 ноября 2011. Архивировано 28 октября 2011 года.
  7. ↑ Vincenti, W. G. and Kruger, C. H. Introduction to physical gas dynamics. — Krieger Publishing Company, 1965. — P. 414.
  8. ↑ S.G Jennings. The mean free path in air (англ.) // Journal of Aerosol Science. — 1988-04. — Vol. 19, iss. 2. — P. 159–166. — doi:10.1016/0021-8502(88)90219-4. Архивировано 8 марта 2021 года.

Ссылки[править | править код]

  • Длина свободного пробега — статья из Физической энциклопедии
Источник

Добавить комментарий