Как найти длину тени физика – Сайт, где вы сможете решить свои вопросы

Условие задачи:

В дно водоема глубиной 2 м вбита свая, выступающая из воды на 0,5 м. Найти длину тени от сваи на дне водоема при угле падения лучей 30°.

Задача №10.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(H=2) м, (h=0,5) м, (alpha=30^circ), (L-?)

Решение задачи:

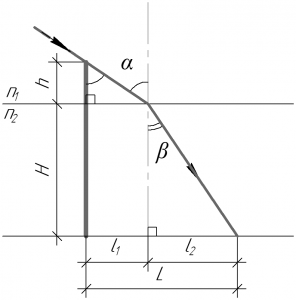Схема к решению задачи Из-за того, что луч при переходе из воздуха в воду претерпевает преломление, то длина тени сваи будет короче, чем на воздухе (см. рисунок к задаче). При этом длину тени сваи на дне пруда можно определить как сумму:

[L = {l_1} + {l_2};;;;(1)]

При этом из прямоугольных треугольников можно найти длины (l_1) и (l_2) по следующим формулам:

[left{ begin{gathered}
{l_1} = h cdot tgalpha hfill \
{l_2} = H cdot tgbeta hfill \
end{gathered} right.]

То есть формула (1) примет вид:

[L = h cdot tgalpha + H cdot tgbeta;;;;(2)]

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

[{n_1}sin alpha = {n_2}sin beta]

Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.

Тогда:

[sin beta = frac{{{n_1}sin alpha }}{{{n_2}}}]

[beta = arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right)]

Полученное выражение подставим в формулу (2), тогда:

[L = h cdot tgalpha + H cdot tgleft( {arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right)} right)]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

[L = 0,5 cdot tg30^circ + 2 cdot tgleft( {arcsin left( {frac{{1 cdot sin 30^circ }}{{1,33}}} right)} right) = 1,1;м]

Ответ: 1,1 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.3.23 В дно пруда вертикально вбита свая так, что она целиком находится под водой. Определите
10.3.25 Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько
10.3.26 Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя

Источник

Геометрическая оптика: тень

Этой статьей я открываю серию статей по геометрической оптике. Все, что нам понадобится – это знания по элементарной тригонометрии: геометрические определения синуса, косинуса, тангенса угла и понятие о подобии треугольников.

Задача 1.

Ученик заметил, что палка длиной 1,2 м, поставленная вертикально, отбрасывает тень длиной 0,8 м. Длина тени от дерева в то же время оказалась ровно в 12 раз больше длины палки. Какова высота дерева?

Так как лучи света мы считаем прямолинейными, то задача сводится к подобию треугольников и определению сходственных сторон.

Геометрическая_1

К задаче 1

Тогда для подобных треугольников $ABC$ и $DEF$ запишем отношение сходственных сторон:

$\frac{AB}{DE}=\frac{AC}{DF}$

Определяем $DE$ :

$DE=\frac{AB\cdotDF}{AC}=\frac{AB\cdot12AB}{AC}=\frac{1,2^2\cdot12}{0,8}=21,6$
Ответ: высота дерева 21,6 м.

Геометрическая_2

К задаче 2

Задача 2.

Уличный фонарь висит на высоте 4 м. Какой длины тень отбросит палка высотой 1 м, если ее установить вертикально на расстоянии 3 м от основания столба, на котором укреплен фонарь?

Запишем отношение сходственных сторон для треугольников $KPO$ и $MNO$ :

$\frac{KP}{MN}=\frac{PO}{NO}$

$\frac{4}{1}=\frac{3+x}{x}$

$3+x=4x$

$x=1$

Ответ: 1 м.

Задача 3.

Уличный фонарь висит на высоте 3 м от поверхности земли. Тень от палки длиной $1,2$ м, установленной вертикально на некотором расстоянии от столба в точке А, равна 0,8 м. Когда палку переместили в другую точку В, длина тени оказалась равной 1,2 м. Каково расстояние между точками А и В? Известно, что основание столба и точки А и В лежат на одной прямой.

Сначала рассмотрим первую ситуацию.

Геометрическая_3

К задаче 3

Запишем отношение сходственных сторон для треугольников $KPO$ и $MAO$ :

$\frac{KP}{MA}=\frac{PO}{AO}$

$\frac{3}{1,2}=\frac{AO+0,8}{0,8}$

$AO+0,8=\frac{3\cdot0,8}{1,2}=2$

$AO=1,2$

Теперь все то же для второго состояния, когда палку передвинули.

Запишем отношение сходственных сторон для треугольников $KPO$ и $MBO$ :

$\frac{KP}{MB}=\frac{PO}{BO}$

$\frac{3}{1,2}=\frac{BO+1,2}{1,2}$

$BO+1,2=\frac{3\cdot1,2}{1,2}=3$

$BO=1,8$

Расстояние между точками $A$ и $B$ равно $BO-AO=1,8-1,2=0,6$

Ответ: 0,6 м.

Задача 4.

На какой высоте висит уличный фонарь, если тень от вертикально установленной палки высотой 0,9 м имеет длину 1,2 м и при перемещении палки на 1 м от фонаря вдоль направления тени длина тени увеличилась до 1‚5 м?

Геометрическая_4

К задаче 4

Задача аналогична предыдущей. Составим отношение сходственных сторон

для треугольников $KPO$ и $MAO$ :

$\frac{KP}{MA}=\frac{PO}{AO}$

$\frac{H}{0,9}=\frac{PA+1,2}{1,2}$

Запишем отношение сходственных сторон для треугольников $KPO$ и $MBO$ :

$\frac{KP}{MB}=\frac{PA+1+BO}{BO}$

$\frac{H}{0,9}=\frac{PA+1+1,5}{1,5}$

Приравняем правые части:

$\frac{PA+1,2}{1,2}=\frac{PA+1+1,5}{1,5}$

$(PA+1,2)1,5=1,2(PA+2,5)$

$1,5PA-1,2PA=1,2(2,5-1,5)$

$0,3PA=1,2$

$PA=4$

Тогда высота подвеса фонаря равна

$H=\frac{0,9(PA+1,2)}{1,2}=3,9$

Ответ: 3,9 м

Задача 5.

На какой высоте $H$ находится аэростат, если с башни высотой $h$ он виден под углом $\alpha$ над горизонтом, его изображение в озере видно под углом $\beta$ под горизонтом?

Геометрическая_5

К задаче 5

От изображения аэростата до поверхности воды такое же расстояние, как и от аэростата до воды.

Тогда $2H=QL+LZ$

Из треугольника $LQT$

$\frac{QL}{LT}=\operatorname{tg}{\alpha}$

$LT=\frac{QL}{\operatorname{tg}{\alpha}}$

А из треугольника $LZT$

$\frac{ZL}{LT}=\operatorname{tg}{\beta}$

$LT=\frac{ZL}{\operatorname{tg}{\beta}}$

Приравняем правые части:

$\frac{QL}{\operatorname{tg}{\alpha}}=\frac{ZL}{\operatorname{tg}{\beta}}$

$ZL=\frac{QL\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}$

Тогда

$2H=QL+\frac{QL\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}=QL\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)= (H-h)\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)$

$H=\frac{(H-h)}{2}\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)$

$H=\frac{H}{2}\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)-\frac{h}{2}\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)$

$\frac{H}{2}\left(\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}-1\right)=\frac{h}{2}\left(1+\frac{\operatorname{tg}{\beta}}{\operatorname{tg}{\alpha}}\right)$

$H=h\cdot \frac{\operatorname{tg}{\beta}+\operatorname{tg}{\alpha}}{\operatorname{tg}{\alpha}}\cdot \frac{\operatorname{tg}{\alpha}}{\operatorname{tg}{\beta}-\operatorname{tg}{\alpha}}$

$H=h \cdot \frac{\operatorname{tg}{\beta}+\operatorname{tg}{\alpha}}{\operatorname{tg}{\beta}-\operatorname{tg}{\alpha}}$

Ответ: $H=h\cdot \frac{\operatorname{tg}{\beta}+\operatorname{tg}{\alpha}}{\operatorname{tg}{\beta}-\operatorname{tg}{\alpha}}$

Источник

Для решения задачи будем использовать законы геометрической оптики и тригонометрии.

1. Глубина водоема равна разности высоты опоры и высоты ее возвышения над поверхностью озера: h = 1.58 / 2 – 0.79 = 0.23 м.

2. Угол падения светового луча на поверхность воды равен 45 градусов, так как он падает под углом к горизонту равному углу между лучом и горизонтом, который в задаче равен 45 градусам.

3. Из закона Снеллиуса найдем угол преломления: sin(alpha) / sin(beta) = 1 / sqrt(2), откуда beta = arcsin(sin(alpha) / sqrt(2)) = arcsin(sin(45) / sqrt(2)) ≈ 31.7 градусов.

4. Чтобы найти длину тени L, найдем сначала длину проекции опоры на дно озера X. Рассмотрим прямоугольный треугольник, составленный из опоры, ее тени на дне озера и луча света, падающего на опору под углом 45 градусов. Тогда гипотенузой треугольника будет высота опоры над поверхностью озера (0.79 м), вертикальной катет будет глубина водоема (0.23 м), а горизонтальный катет – искомая проекция опоры на дно озера X. Используем теорему Пифагора:

0.79² = X² + 0.23²

X² = 0.79² – 0.23²

X ≈ 0.749 м

Теперь найдем длину тени на дне озера, сложив длину проекции опоры на дно озера и длину самой тени, которая равна X * tg(beta):

L = X + X * tg(beta) ≈ 0.749 + 0.463 ≈ 1.212 м

Ответ: глубина водоема h ≈ 0.23 м, угол падения света на поверхность воды alpha = 45 градусов, угол преломления света в воде beta ≈ 31.7 градусов, длина тени на дне озера L ≈ 1.212 м.

Источник

В солнечный день длина тени на земле от ели высотой 1,8 м равна 90 см, а берёзы — 10 м. Какова высота берёзы?

(Перышкин. Физика. 8 класс. Задачи для повторения, № 47)

Мой подход к решению этой задачи по физике, наверное, самый простой споб, без всяких формул. Итак, поехали.

Во-первых, нужно определить, длина тени на земле от ели во сколько раз меньше высоты данной ели. Для этого размер высоты ели (1,8 метра)разделим на длину тени ели на земле (90 сантиметров, или 0,9 метра): 1,8метров/0,9метров = 2 раза;

Таким образом, выяснили, что длина тени ели в два раза меньше её высоты. Значит, и тень берёзы во столько же раз будет меньше высоты этой берёзы.

Для того, чтобы найти высоту берёзы, умножим на два длину тени берёзы (10 метров) и получим её высоту: 10*2=20.

Ответ: высота берёзы составляет 20 метров.

Winiki
[166K]

1 неделю назад

В этой задаче источником света является звезда по имени Солнце. А находится оно от поверхности Земли очень далеко – примерно 150 млн километров, а потому падающие лучи можно считать параллельными. Что касается деревьев, то я предлагаю мысленно предположить, что берёза и ель растут из одного места. Выглядеть это могло бы следующим образом:

Тени от ели и берёзы

Тогда мы имеем два треугольника, у которых:

общее основание – поверхность Земли;
общая сторона от корней до макушки ели, которая перпендикулярна основанию и потом продолжается до макушки берёзы;
третьи стороны не совпадают, но параллельны друг другу.

По всем признакам мы имеем, во-первых, два прямоугольных треугольника. А, во-вторых, они подобны, потому что две параллельные прямые пересекают третью под одинаковым углом. Если имеет место подобие, тогда высота берёзы будет относиться к высоте ели точно так же, как и длина тени от большего дерева к длине тени от меньшего:

H(б) / H(е) = L(б) / L(е)
H(б) / 1,8 = 10 / 0,9
H(б) = 1,8 * 10 / 0,9
H(б) = 20 метров

Очевидно, что берёзка выдалась высокой – её высота равна двадцати метрам, потому и тень такая длинная. А ёлочка ещё молоденькая – она маленькая сама и тень её существенно короче.

Ответ: Высота берёзы составляет 20 метров.

Знаете ответ?

Смотрите также:

ВПР 8 класс, Как решить задачу об автомобилисте, возвращавшегося с дачи?

ВПР физика 8 класс Задание 11 № 811 – какой ответ?

ВПР по физике 8 класс 2020, задания, ответы, демоверсии, где найти?

Физика 8 класс, Доклад на тему: “Круговорот воды в природе”, как написать?

Физика 8 класс, Доклад на тему: “Лунное затмение”, как написать?

Физика 8 класс, Доклад на тему: “Солнечное затмение”, как написать?

ВПР Физика 8 класс, задание 2 № 26 – какой ответ?

ВПР Физика 8 класс, задание если замёрзли руки, ответ – где найти?

ВПР 8 класс, Как выполнить задания про Антона, пытающегося сварить мыло?

ВПР 8 класс, Как описать происходящее с магнитной стрелкой в электроцепи?

Источник

Тип 10 № 5119 Добавить в вариант

Сообщить об ошибке

В дно водоема глубиной 2 м вбита свая, на 0,5 м выступающая из воды. Найти длину тени от сваи на дне водоема при угле падения лучей 70°.

Спрятать решение

Решение.

По закону преломления света дробь: числитель: синус альфа , знаменатель: синус гамма конец дроби =n, откуда находим, что синус гамма = дробь: числитель: синус альфа , знаменатель: n конец дроби .

Найдем косинус и тангенс угла преломления:

косинус гамма = корень из: начало аргумента: 1 минус синус в квадрате гамма конец аргумента = дробь: числитель: корень из: начало аргумента: n в квадрате минус синус в квадрате альфа конец аргумента , знаменатель: n конец дроби ;

тангенс гамма = дробь: числитель: синус гамма , знаменатель: косинус гамма конец дроби = дробь: числитель: синус альфа , знаменатель: корень из: начало аргумента: n в квадрате минус синус в квадрате альфа конец аргумента конец дроби .

Тогда найдем длины отрезков OC и СB:

OB=h тангенс альфа , OB=H тангенс гамма = дробь: числитель: H синус альфа , знаменатель: корень из: начало аргумента: n в квадрате минус синус в квадрате альфа конец аргумента конец дроби .

Следовательно, длина тени от сваи равна

OC=BC плюс OB=h тангенс альфа минус дробь: числитель: H синус альфа , знаменатель: корень из: начало аргумента: n в квадрате минус синус в квадрате альфа конец аргумента конец дроби =
=0,5м умножить на тангенс 70 градусов минус дробь: числитель: 2м умножить на синус 70 градусов градусов , знаменатель: корень из: начало аргумента: 1,33 в квадрате минус синус в квадрате 70 градусов конец аргумента конец дроби approx3,4м.

Ответ: 3,4 м.

Источник: Рымкевич А. П. Сборник задач по физике для 9−11 классов, М.: «Просвещение», 1990 (№ 1034)

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 1,1 м.

Смотрите также задачи:

Геометрическая оптика: тень

Вам также может понравиться

Как правильно составить вопрос на английском с did

Оскорбила человека как исправить

Мультфильм по берестову как нашли друг друга

Добавить комментарий Отменить ответ