Как найти длину теодолитного хода

Теодолитный ход является наиболее востребованной частью геодезических работ, переплетаясь со многими видами инженерной деятельности. В чем же его назначение и какие особенности выполнения разберем по порядку в нашей статье.

Назначение и основные разновидности

Проводится с целью точного отображения местности и расположенных на ней объектов на крупномасштабной карте, плане или специальных схемах.

Данная процедура подразумевает создание системы точек, закрепленных в натуре, и определение их горизонтальных углов при помощи теодолита или тахеометра. Расстояние между пунктами определяется при помощи светодальномеров, рулеток и других приборов, позволяющих обеспечить необходимую точность. По форме обычно принято различать следующие виды ходов:

– разомкнутый;

– замкнутый;

– висячий.

В разомкнутом первая и последняя точка базируется на разные пункты и направления геодезической сети, чьи координаты и дирекционные углы уже определены, а замкнутый образует геометрическую фигуру, поэтому может опираться только на один. Особенность же висячего хода состоит в том, что один его конец примыкает к пункту геодезического обоснования, а второй остается свободным.

Его форма во многом зависит от того, на какой территории проводятся измерения. Например, для автодорог и трубопроводов хорошо подойдет разомкнутый ход, а на строительных площадках и земельных участках обязательно должен быть построен замкнутый полигон.

Достаточно распространённой процедурой является прокладывание внутри больших полигонов дополнительных сетей, чтобы полностью отобразить ситуацию на плане.

Порядок проведения

Выполнение теодолитного хода начинают с рекогносцировки, подразумевающей изучение ее особенностей и определение наиболее подходящих мест для установки точек.

Расстояние между ними должно варьироваться в пределах от 20 до 350 метров, но оно зависит также и от масштаба съемки. Наилучшей точности можно добиться, если расстояние будет одинаковым, но особенности территории далеко не всегда позволяют это сделать.

Съемку осуществляют на открытом пространстве с хорошей взаимной видимостью между пунктами, закрепленными специальными кольями из дерева, металла и других материалов. Для их долговременной сохранности нередко используются бетонные монолитные столпы. Также рекомендуется привязать каждый знак к твердым объектам поблизости, чтобы можно было восстановить его в случае потери.

Когда все подготовительные процедуры завершены и определено местоположение пунктов начинаются полевые работы. Прибор устанавливают на точке и измеряют угол за один прием, визируясь на соседние, после чего определяют расстояния между ними.

Если строится замкнутый полигон, за начальный берут магнитный азимут одной из сторон. Привязка к пункту геодезической сети необходима для определения дирекционного угла и координат, что позволит обеспечить должный контроль полученных результатов.

Все данные записываются в специальный журнал или автоматически заносятся в память электронного измерительного устройства. В дальнейшем они используются для камеральной обработки, которая подразумевает проведение расчетов с целью вычисления координат пунктов и жестких контуров.

Параллельно со съемкой составляется схематический чертеж, отображающий местоположение объектов на местности, который называется абрисом. Он представляет собой полноценный документ, является неотъемлемой частью технической документации и служит источником информации при построении плана или карты.

Во время составления абриса необходимо отобразить на нем как можно больше информации. Особенно важно обозначить все метрические данные и сделать его понятным для прочтения.

Во время снегопада, дождей и других неблагоприятных погодных условий, а также при плохой освещенности, проводить измерения запрещается.

Основные технические требования к линейным измерениям

Любые геодезические работы должны быть выполнены с четким соблюдением всех правил, дабы обеспечить получение самых точных результатов измерений. Основные требования к данной процедуре изложены в инструкции по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500, а также ряда других нормативных документов.

В зависимости от предельной относительной погрешности  длина теодолитного хода должна соотносится со следующими показателями, приведенными в табл.1.

Таблица 1.

Буровая установка	№ скважины	Литологический тип	Коэф. крепости	Размер отдельности, м	Скорость фактическая, м/c
DM LP	6,0	4,0	2,0	6,0	3,0
СБШ	3,0	2,0	1,0	3,6	1,5
1:1000	1,8	1,2	0,6	1,5	1,5
1:500	0,9	0,6	0,3	—	—

(m_{s}) – среднеквадратическая ошибка измеренных расстояний.

Показатели предельно допустимых длин между узловой точкой и исходной уменьшается на 30%, а также должны быть:

– больше 20 м, но меньше 350 м на застроенных участках;

– свыше 40 м и не более 350 м.

Аналогичные требования (табл. 2) есть и к висячим теодолитным ходам:

Таблица 2.

Масштаб	Местность
Застроенная	Не застроенная
1:5000	350	500
1:2000	200	300
1:1000	150	200
1:500	100	150

Измерение длин необходимо проводить в обе стороны и высчитать их среднее значение, а точность приборов должна быть не менее 30”. Допустимое отклонение при центрировании – не более 3 мм.

Съемка ситуации и ее виды

Прокладывание теодолитного хода, как правило, проводят для последующего отображения особенностей территории работ. Конечная цель – получения данных о местоположении снимаемых объектов в пространстве и составление контурной карты или плана местности без отображения рельефа. Фиксируются наиболее значимые элементы окружения:

– деревья и крупная растительность;

– инженерные конструкции;

– государственные геодезические пункты;

– контуры зданий, сооружений и других жестких объектов.

Процесс их измерения называется съемкой ситуации, которая выполняется следующими способами:

1. Способ перпендикуляров. Применяют для съемки объектов вытянутой формы, которые расположены преимущественно на открытом пространстве и близко к пунктам. Основной принцип выполнения этого способа строится на определении основания перпендикуляра, а также измерении его длины до станции.
2. Полярных координат. Проводится, если снимаемая цель находится на большом расстоянии от пункта. Одна сторона принимается за полярную ось, а ее вершина – за полюс. Измеряются горизонтальные углы направления на заданную точку и определяют линейное расстояния до нее.
3. Угловая засечка. Хорошо подходит для съемки труднодоступных точек. Их местоположение определяют совмещением сторон углов, измеренных от вершины теодолитного хода до заданного пункта с двух направлений.
4. Метод створа (линейных промеров) используется, когда контуры местности пересекают уже построенный ход или его продолжение, а также для определения дополнительных точек посредством линейных измерений. Данный способ активно применяется на сильно застроенных участках.
5. Способ обхода используют, как правило, на закрытой местности, если необходимо снять особо важный объект, но от вершин сторон это сделать невозможно по причине наличия препятствий или дальности. Прокладывают дополнительные пикеты, которые и привязывают к основным пунктам, а границы контура снимают методом перпендикуляра.

Геодезические работы основаны на принципе «от общего к частному». Поэтому, в теории, лучше всего сперва построить теодолитный ход, а потом уже провести съемку подробностей.

Обработка полученных результатов измерений

Выполнение контурной съемки проводится с целью получения данных, необходимых для дальнейшего расчета координат:

– горизонтальных углов;

– длин сторон теодолитного хода;

– дирекционных углов;

– румбов.

Подсчет теоретической суммы угловых измерений () хода осуществляют по формуле (табл. 3).

Таблица 3.

замкнутый	разомкнутый
(beta _{T}= 180left ( n-2 right ))	(beta _{T}=left ( alpha _{р}+alpha _{к} right )pm 180^{o}cdot left ( n+1 right ))

n – количество точек;

(alpha _{н})– значение начального дирекционного угла, –конечного;

Далее производят расчет угловой невязки:

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

(f_{beta }=sum beta _{изм}- sum beta _{т})

(beta _{изм})– сумма измеренных углов.

Следующим шагом будет сравнение  (f_{beta })с допуском (f_{beta доп}). Если результат не соответствует приведенному ниже выражению, необходимо перепроверь данные:

(f_{beta}< f_{beta доп})

(f_{beta доп}={1,5·t}sqrt{n}), где t – приборная точность измерения углов; n – количество измеряемых углов.

В дальнейшем  (f_{beta}) равномерно распределяется между измеренными величинами с противоположным знаком и проводится расчет поправки измеренных углов ((delta _{beta })):

(delta _{beta} = – frac{f_{beta }}{n})

При правильном выполнении расчетов сумма поправок будет иметь отрицательное значение:

(sum delta _{beta }=-f_{beta })

Далее следует вычисление дирекционного угла (α), который начинают отчитывать от северного направления осевого меридиана по часовой стрелке.

(alpha _{n}=alpha _{n-1}+180^{o}-beta _{пр.исп})

(alpha _{n}=alpha _{n-1}-180^{o}+beta _{л.исп})

В данном выражении  (alpha _{n-1})– дирекционный угол предыдущей точки, (alpha _{n})– последующей.

(beta _{пр.исп})– исправленное значение правого по ходу угла,  (beta _{л.исп})– исправленное значение левого по ходу угла.

Начальный α должен равняться конечному. Если же полученный α больше 360°, то перед тем, как занести показатели в журнал из них вычитают 360°.

Теперь вычисляется румб (r), который отсчитывают от самого близкого окончания осевого меридиана до ориентированной линии. Рассчитывается в зависимости от своего местоположения относительно четверти координат (табл. 4).

Таблица 4. Формула румба для каждой четверти.

Четверть и ее название	Пределы α	Формула	Знаки приращения координат
ΔХ	ΔУ
1 С.В.	0° – 90°	r = α	+	+
2 Ю.В.	90°-180°	r = 180° – α	–	+
3 Ю.З.	180°-270°	r = α – 180°	–	–
4 С.З.	270°-360°	r = 360° – α	+	–

Приращение геодезических координат определяют:

(X = d · cos(r))

(Y = d · sin(r))

где: d – горизонтальное проложение;

r – румб стороны.

Уравнивание проводят при помощи приведенных ниже формул:

(f_{Delta X}=sum Delta X_{B}-sum Delta X_{T})

(f_{Delta Y}=sum Delta Y_{B}-sum Delta Y_{T})

( sum Delta X_{B})  и (sum Delta Y_{B})– сумма приращений координат, которые были определены с учетом знаков;

(sum Delta X_{T}) и (sum Delta Y_{T})  – теоретическая сумма приращения значений координат.

Стоит отметить, что в замкнутом полигоне последние значение равняются нулю, поэтому невязки должны быть равны сумме приращений или приближенными к нему.

Проверка условия допустимости:

1. Абсолютного значения:

(f_{абс}=sqrt{fDelta X^{2}+fDelta Y^{2}})

2. Относительного:

(f_{отн}=frac{f_{абс}}{P})

где Р – периметр хода (сумма его горизонтальных проложений).

Условие допустимости:

(left | f_{отн} right |leq left | f_{абс} right |)

Невязки раскидывают с обратным знаком, предварительно выполнив поправки на приращение каждой стороны при помощи таких формул:

(delta X_{imath }=frac{f_{x}cdot d_{imath }}{P})

(delta Y_{imath }=frac{f_{Delta y}cdot d_{imath }}{P})

(imath) – номер точки;

Все координаты вершин рассчитываются таким образом:

(X_{n}=X_{n-1}+Delta X_{n-1(исп)})

(Y_{n}=Y_{n-1}+Delta Y_{n-1(исп)})

Составление плана

Полученные в процессе съемки и дальнейшей обработки данные используются для построения картографического материала, как с помощью специальных программ, так и вручную.

Выполняется в крупном масштабе и содержит подробную информацию о местности. Последовательность построения следующая:

1. Создание координатной сетки. Берутся либо уже заранее подготовленные листы или чертятся с помощью линейки Дробышева. Также можно построить ее посредством проведения через плотный лист бумаги двух диагональных линий и последующего откладывания отрезков от их пересечения. Очень важно начертить сетку таким образом, чтобы схема хода и прилегающие территории находились в середине.

Правильность нанесения пунктов на план можно проверить по расстоянию между ними, которое не должно быть больше 0,2 мм. Кроме того, отображают ситуацию на нем при помощи методов, используемых во время полевых работ.

1. Нанесение вершин и отображение ситуации. Точки пикетов отображаются на плане или карте, а потом переносят элементы окружающей местности, которые были предварительно зарисованы на абрисе. Отображаются они в виде символических графических обозначений, передающие информации об объекте, существующем в реальности – условных знаков.
2. Зарамочное оформление. Обязательно указывают в каком масштабе выполнен план и какая местность и ситуация на нем изображена.

На сегодняшний день обработку и создание графических материалов выполняют при помощи специально созданного для этих целей программного обеспечения (ГЕОМИКС). Благодаря ему процессы камеральной обработки стали значительно проще и занимают гораздо меньше времени. Но только на на этом возможности геодезических программ не заканчиваются. Осуществив все необходимые вычисления и уравнивания, можно построить план в электронном виде и распечатать, а в случае необходимости провести коррективы.

Теодолитные
ходы.
Теодолитным ходом называют ход
полигонометрии, выполненный методами,
достаточными для обеспечения точности,
требуемой в съемочных сетях.

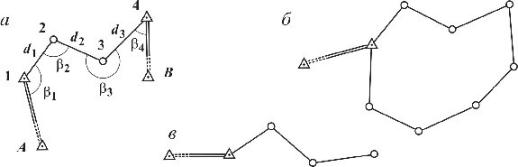
Рис.
6.5. Схемы теодолитных ходов: а –
разомкнутого; б –
замкнутого; в–
висячего.

По
форме теодолитный ход может быть
разомкнутым – опирающимся на два исходных
пункта и два исходных направления (рис.
6.5 а);
замкнутым – опирающимся на один исходный
пункт и одно направление (рис. 6.5 б);
висячим – разомкнутым ходом, опирающимся
на один исходный пункт и одно направление
(рис. 6.5 в).
Теодолитные ходы могут образовать
систему теодолитных ходов с узловыми
точками в местах их соединения (см.
рис. 6.2 б).

Проект
съемочной сети составляют на топографической
карте или плане. Но часто положение
ходов выбирают непосредственно на
местности в процессе рекогносцировки.
При этом учитывают ограничения на длину
хода между исходными пунктами, приведенные
в табл. 6.2. Длины ходов, опирающихся на
узловые точки, уменьшают на 30%.

Таблица
6.2

Масштаб съемки

Открытая местность, застроенная территория Закрытая местность Допустимые относительные невязки 1/3000 1/2000 1/1000 1/2000 1/1000 Допустимая длина теодолитного хода, км

1:5000 1:2000 1:1000 1:500

6,0 3,0 1,8 0,9

4,0 2,0 1,2 0,6

2,0 1,0 0,6 0,3

6,0 3,6 1,5 –

3,0 1,5 1,5 –

 Места
для точек хода выбирают так, чтобы
обеспечить взаимную видимость между
ними, благоприятные условия для съемки
окружающей местности, удобства установки
геодезических приборов и сохранность
точек.

Точки
ходов закрепляют деревянными кольями,
костылями, металлическими трубами и
т.п. Часть точек закрепляют знаками
долговременной сохранности – столбами,
бетонными монолитами.

Углы
поворота теодолитного хода измеряют
электронным тахеометром или теодолитом.
При этом следят, чтобы на всех точках
хода измерялись только правые, или
только левые по ходу углы.

Для
измерения угла в его вершине устанавливают
прибор, а в соседних точках – визирные
цели. Угол измеряют одним приемом.

Длины
сторон измеряют электронным тахеометром
или светодальномером, а при их отсутствии
– землемерной лентой.

Результаты
измерения углов и расстояний записывают
в журналы установленной формы. При
выполнении измерений тахеометром запись
результатов измерений выполняется
автоматически – в памяти прибора, откуда
в последующем они вводятся для обработки
в компьютер.

Обработка
разомкнутого теодолитного хода.
Исходными данными

в
разомкнутом ходе (рис. 6.5 а)
являются координаты начального и
конечного пунктов 1 и 4 (
, 
, 
, 
)
и дирекционные углы начального A-1
и конечного 4-B направлений
(
 и 
).

При
обработке вручную записи ведут в
ведомость установленной формы (табл. 6.3).
В графу 1 вписывают названия или номера
точек. Вписывают исходные данные: в
соответствующие строки графы 3 – начальный
и конечный дирекционные углы, а в графы
7 и 8 – координаты начального и конечного
пунктов (исходные данные в таблице
выделены жирным шрифтом). Вписывают
результаты измерений: измеренные углы
– в графу 2, горизонтальные проложения
сторон хода – в графу 4.

Уравнивание
углов.
Подсчитывают сумму измеренных углов 
.
Теоретически эта сумма должна быть
равна:

для
правых углов – 
;

для
левых углов – 
,

где n –
число измеренных углов. В табл. 6.3 углы
– правые.

Отличие
фактической суммы углов от теоретической
представляет угловую невязку хода:

.
(6.2)

Таблица
6.3

Ведомость
вычисления координат точек теодолитного
хода

Названия точек

Измеренные углы

Дирекционные углы

Длины сторон, м

Приращения координат, м Координаты, м x y

1	2	3	4	5	6	7	8
A
	-0,3¢	349º 50,0′
I	113º 26,0′			-0,03	+0,04	6322,70	4057,25
	-0,3	56 24,3	138,56	+76,67	+115,42
II	85 07,5			-0,03	+0,03	6399,34	4172,71
	-0,3	151 17,1	116,30	–102,00	+55,88
III	211 44,5			-0,04	+0,05	6297,31	4228,62
	-0,3	119 32,9	197,24	–97,27	+171,59
IV	56 33,2					6200,00	4400,26
		243 00,0
B

Sb = 466°51,2′

P = Sd = 452,10

SDx = = –122,60

SDy = = +342,89

	= -122,70;  = 343,01;
= 4×180° –	м
	= + 342,89 – 343,01 = – 0,12 м
	м

Вычисленную
угловую невязку сравнивают с допустимой

.

Если
угловая невязка меньше допустимой, что
указывает на доброкачественность
угловых измерений и правильность
вычислений, то невязку 
 распределяют
поровну во все измеренные углы со знаком,
противоположным знаку невязки. Полученные
при этом поправки

вписывают
над измеренными углами в графу 2. Невязка
редко делится на число углов без остатка.
Поэтому поправки округляют, вводя
бо¢льшие в углы с более короткими
сторонами. При этом сумма поправок
должна равняться невязке с обратным
знаком: Sd_b =
–f_b.

Вычисление
дирекционных углов. Дирекционные
углы вычисляют, используя начальный
дирекционный угол 
и
измеренные углы b_i,
исправленные поправками d_b,
по формулам:

для
правых углов – 
;

для
левых углов – 
.

Здесь
индексы i =
1, 2, …, n соответствуют
номерам углов и сторон на рис. 6.5 а,
причем a₀ =
a_нач и
a_n =
a_кон.

Контролем
правильности вычислений служит равенство
вычисленного и заданного значений
конечного дирекционного угла.

Вычисление
приращений координат выполняют
по дирекционным углам и длинам сторон
хода (графы 5 и 6).

; 
 (i =
1, 2, …, n-1).

Вычислив
суммы приращения абсцисс 
 и
ординат 
,
находят координатные невязки

, 
 .
(6.3)

Вычисляют
абсолютную невязку
 и
относительную невязку хода f / P, где 
 –
длина хода. Если относительная невязка
не превосходит допустимой (обычно,
1/2000), то невязки f_x и f_y распределяют
(см. записи курсивом в графах 5 и 6), в виде
поправок к приращениям
координат, пропорциональных
длинам сторон, и со знаками, противоположными
знакам невязок:

; 
.
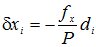
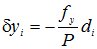
(6.4)

Суммы
поправок должны равняться невязкам с
обратным знаком:

; 
.

Если
из-за выполненных округлений равенства
нарушаются, поправки, вычисленные по
формулам (6.4), несколько изменяют,
добиваясь соблюдения равенств.

Вычисление
координат точек
теодолитного хода выполняют по формулам
(см. графы 7 и 8)

; 
 (i =
1, 2, …, n-1).

Контролем
правильности вычислений служит совпадение
вычисленных и заданных координат
последней точки теодолитного хода.

Обработка
замкнутого теодолитного хода.

Последовательность
обработки замкнутого хода такая же как
и разомкнутого. Но исходными в замкнутом
теодолитном ходе служат координаты
одного из пунктов хода и дирекционный
угол одной из сторон. Это накладывает
на обработку замкнутого хода следующие
особенности.

Угловая
невязка вычисляется по формуле (6.2), в
которой в отличие от разомкнутого хода

,

где n –
число углов в полигоне.

После
распределения угловой невязки и
вычисления дирекционных углов сторон
хода контролируют правильность вычислений
– в конце должно быть получено то же
значение дирекционного угла, которое
было исходным.

Невязки
в координатах находят по формулам:

, 
.

Эти
соотношения следуют из формул (6.3), где
в данном случае 
, 
.
Распределив невязки f_x и f_y и
вычислив координаты точек хода,
контролируют правильность вычислений
– вычисленные в конце координаты начальной
точки хода должны равняться исходным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Основные виды теодолитного хода.

Теодолитный ход – это разомкнутая или замкнутая ломаная линия. В зависимости от формы построения, различают несколько видов ходов:

Разомкнутый теодолитный ход, опирающийся на два пункта с известными координатами и два дирекционных угла. Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.

Разомкнутый теодолитный ход, опирающийся на один исходный пункт и один дирекционный угол – такой ход еще называют висячим. Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.

Замкнутый ход по своей сути является многоугольной фигурой и опирается только на один базовый пункт с установленными координатами и дирекционным углом. Вершинами стороны выступают точки, закрепленными на местности, а отрезками – расстояние между ними. Его чаще всего создают для съемки стройплощадок, жилых зданий, промышленных сооружений или земельных участков.

Диагональный (прокладывают внутри других ходов). Если необходимо заснять ровный участок, вроде строительной площадки, лучшим выбором будет полигон. На объектах вытянутого типа, вроде автодорог, принято использовать разомкнутый ход, а висячий – для съемки закрытой местности, вроде глухих улиц

Порядок выполнения работ

Как и другие геодезические мероприятия, эта процедура проводится с предварительной подготовкой для получения точных метрических данных. Немаловажную роль играет также их математическая обработка. Сами работы выполняются по принципу от общего к частному и состоят из следующих этапов:
1. Рекогносцировка местности. Оценка снимаемой территории, изучение ее особенностей. На этом этапе определяется местоположение снимаемых точек.
2. Полевая съемка. Работы непосредственно уже на местности. Выполнение линейных и угловых измерений, составление абрисов, предварительные расчеты и внесение изменений при необходимости.
3. Камеральная обработка. Завершающий этап работ, который заключается в вычислении координат замкнутого теодолитного хода и последующего составления плана и технического отсчета.

Рекогносцировка и полевые измерения выполняются непосредственно на объекте и являются наиболее трудоемкими и затратными мероприятиями. Тем не менее, от качества их проведения зависит дальнейший результат.
Обработка данных проводится уже в помещении. Сегодня она осуществляется при помощи специального программного обеспечения, хотя и ручные расчеты все также остаются актуальными и могут быть использованы геодезистом в целях проверки.

Обработка данных

Обработка результатов измерений замкнутого теодолитного хода позволит оценить качество проделанной работы и внести исправления в полученные геометрические величины. Чтобы убедится в том, что угловые и линейные измерения находятся в допуске, еще во время полевых работ выполняют первичные расчеты.
Для вычисления значений координат точек замкнутого хода используют такие данные:     – координаты исходного пункта;
– исходный дирекционный угол;
– горизонтальные углы;
– длины сторон.

Уравнивание

При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.

∑βтеор=180∘⋅(n−2)

n- количество точек полигона

fβ=∑βизм−180∘⋅(n−2)

∑βизм – значение измеренных угловых величин;

Для получения fβ, необходимо рассчитать разность между βизм, в которой присутствуют погрешности, и ∑βтеор.

В уравнивании fβ выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:

fβ1=1,5tn−−√

t-точность измерительного устройства,
n – количество углов.
Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.

Определение дирекционных углов

При известном значении дирекционного угла (α) одной стороны и горизонтального (β) можно определить значение следующей стороны:

αn+1=αn+η
η=180∘−βпр

βпр – значение правого по ходу угла, из чего следует:

αn+1=αn+180∘−βпр

Для левого (βлев) эти знаки будут противоположными:

αn+1=αn−180∘+βлев

Поскольку значение дирекционного угла не может быть больше, чем 360∘, то из него, соответственно, отнимают 360∘. В случае с отрицательным углом, необходимо к предыдущему α добавить 180∘ и отнять значение βиспр.

Вычисление румбов

У румбов и дирекционных углов существует взаимосвязь, а определяют их по четвертям, которые носят название четырех сторон света. Как видно из табл.1. расчёты проводят согласно установленной схеме.

Таблица 1. Расчеты румба в зависимости от пределов дирекционного угла.

Приращения координат

Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:

ΔX=d⋅cosα
ΔY=d⋅sinα

d-горизонтальное проложение;
α-горизонтальный угол.

Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:

∑ΔXтеор=0
∑ΔYтеор=0

Линейная невязка и невязка приращения значений координат

Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:

fx∑ni=1ΔX1
fy∑ni=1ΔY1

Переменные fx и fy – проекции линейной невязки fp на координатной оси, которую можно рассчитать по формуле:

fp=f2x+f2y−−−−−−√

При этом fp, не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения fx и fy проводится следующим образом:

δXi=−fxPdi
δYi=−fyPdi

В этих формулах δXi и δYi – поправки приращения координат.
і- номера точек;

После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.

Вычисление координат

Когда будут произведены увязки приращений точек полигона, следует определение координат, которое осуществляют с использованием следующих формул:

Xпос=Xпр+ΔXисп
Yпос=Yпр+ΔYисп

Значения Xпос Yпос – координаты последующих пунктов, Xпр и Yпр – предыдущих.
ΔXисп и ΔYисп – исправленные приращения между этими двумя значениями.
Если координаты первой и последней точки совпадают, то обработку можно считать завершённой.
На основе полученных координат и составленных во время полевых измерений абрисов в дальнейшем составляется план теодолитного хода.

Измерение длин сторон теодолитного хода

---

Добавлено Serxio 14-03-2017, 17:01 Просмотров: 9 252