Прямоугольный параллелепипед строится на ребрах трех длин, расположенных под прямым углом друг к другу. Зная ребра параллелепипеда, можно найти все возможные параметры, характеризующие его. В первую очередь, каждая грань параллелепипеда представляет собой прямоугольник с двумя одинаковыми сторонами, периметр же всего объемного тела ищется как умноженная на четыре сумма всех сторон-ребер параллелепипеда.
P=4(a+b+c)
Площадь прямоугольного параллелепипеда складывается из площадей всех его граней, то есть шести прямоугольников, попарно конгруэнтных. Площадь каждого прямоугольника равна произведению его сторон, поэтому чтобы найти площадь параллелепипеда, необходимо сложить эти произведения.
S=2ab+2bc+2ac=2(ab+bc+ac)
Чтобы вычислить объем прямоугольного параллелепипеда, зная его ребро, нужно перемножить их между собой, так как объем любого прямого тела с двумя основаниями равен произведению площади основания на высоту тела, а в основании параллелепипеда находится прямоугольник, площадь которого также равна произведению – его сторон.
V=abc
У прямоугольного параллелепипеда есть четыре диагонали – диагонали его боковых граней и основания, и диагональ самого параллелепипеда, проходящая через его внутреннее пространство. Все диагонали рассчитывается через прямоугольные треугольники по теореме Пифагора, где они являются гипотенузами. Для диагоналей боковых граней и основания катетами являются ребра параллелепипеда, а для четвертой диагонали, катеты представляют собой боковое ребро и диагональ основания. (рис. 22.1,22.2,22.3,22.4)
d_1=√(a^2+c^2 )
d_2=√(a^2+b^2 )
d_3=√(b^2+c^2 )
d_4=√(a^2+〖d_3〗^2 )=√(a^2+b^2+c^2 )
Угол α, образованный внутренней диагональю прямоугольного параллелепипеда и диагональю основания, можно вычислить через отношение тангенса – бокового ребра а и диагонали основания d3.(рис.22.5)
tanα=a/d_3 =a/√(b^2+c^2 )
Пусть a, b, c − измерения параллелепипеда. Воспользовавшись формулой объема параллелепипеда, выполните следующие задания:
1) Вычислите неизвестную длину третьего ребра параллелепипеда, если:
а) V = 48
с
м
3
, b = 3 см, c = 4 см;
б) V = 210
с
м
3
, b = 6 см, c = 7 см;
в) V = 24
с
м
3
, a = 3 м, b = 2 м.
2) Выразите длину какого−либо ребра параллелепипеда через его объем и длины двух других ребер.

reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 8.3 Формулы. Вычисления по формулам. Номер №662
Решение 1
а) a = V : (b * c) = 48 : (3 * 4) = 4 (см);
б) b = V : (a * c) = 210 : (6 * 7) = 210 : 42 = 5 (см);
в) c = V : (a * b) = 24 : (3 * 2) = 24 : 6 = 4 (см).
Решение 2
V = abc, значит:
a = V : (b * c);
b = V : (a * c);
c = V : (a * b).
По условию известны длины двух ребер паралелепипеда и площадь его поверхности (displaystyle S_п=166 { small .})
Требуется найти длину третьего ребра.
Пусть (displaystyle c ) – длина третьего ребра.
Площадь поверхности параллелепипеда (displaystyle S_п)– это сумма площадей поверхности всех его граней.
Грани прямоугольного параллелепипеда – прямоугольники. Найдем их площади.
|
Верхняя и нижняя грани: (displaystyle S_1=7 cdot 4) |
Фронтальная и задняя грани: (displaystyle S_2=7 cdot c) |
Боковые грани: (displaystyle S_3=4 cdot c) |
Тогда площадь поверхности параллелепипеда
(displaystyle S_п=2S_1+2S_2+2S_3)
или
(displaystyle S_п=2(S_1+S_2+S_3){small .})
Подставляя найденные выражения для (displaystyle S_1 { small ,} , S_2 { small ,} , S_3 ) и (displaystyle S_п=166 { small ,}) получаем:
(displaystyle 166=2cdot( 7 cdot 4+7 cdot c +4 cdot c){ small .})
Решим полученное уравнение и найдём (displaystyle c{ small :})
(displaystyle 2cdot( 28+11 cdot c)=166,text{Large |} : color{red}{ 2}{ small ,} )
(displaystyle 28+11c=83{ small ,} )
(displaystyle 11c=55{ small ,} )
откуда
(displaystyle c=5{small .} )
Значит, длина третьего ребра параллелепипеда равна (displaystyle 5{small .} )
Ответ: (displaystyle 5{small .})
-
Математика
Предыдущий вопрос
Следующий вопрос
lenchiky
3 года назад
Ответ
Ответ дан
8Madina8
Решение:
4*3+4*7=12+28=40
252-40=212(сумма 4-х высот )
212/4=53(измерение 3-е)
Ответ:53см
Ответ
Ответ дан
sasha1507
Ответ: у параллелепипеда 4 ширины, 4 высоты, 4длины, поэтому
сумма длин всех ребер
L= 4*(а+в+с)
4*3+4*7=12+28=40 см
252-40= 212 это сумма 4 высот
212:4=53 см это третье измерение
Ответы и объяснения
- lenchiky
Не тот ответ, который тебе нужен?
Найди нужный
![]()
0
Как решить задание (ЕГЭ и ОГЭ) по математике? Какой ответ?
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

1 ответ:
![]()
0
0
Формула для нахождения объема параллелепипеда через стороны: V=abc, где a, b, c — стороны параллелепипеда. Поэтому третье ребро найдем по формуле: c=V/ab=48/12=4
Читайте также
![]()
В пространстве целых 4 возможных варианта расположения двух прямых:
1)Две прямые совпадают
2)Две прямые пересекаются в одной точке
3)Две прямые параллельны
(Прямые называются параллельными, если выполняется два условия:
они не имеют общих точек
и существует плоскость, содержащая обе эти прямые)
4)Две прямые скрещиваются
(Прямые называются скрещивающимися, если не существует плоскости, которая бы содержала обе эти прямые)
Надо отметить, что на плоскости возможны только 3 из этих 4 вариантов (всё кроме последнего). И, соответственно, определение параллельности в планиметрии (наука, изучающая свойства фигур на плоскости) звучит немного по-другому (без второго пункта).
![]()
Попробую объяснить логическую задачу, как поняла я.
1.Футболист – самый младший, нет браты , нет сестры.
2.Миша старше боксера, значит и старше футболиста – самый старший.
3.Дима – есть сестра, он средний (Саша моложе, а Миша старше).
4.Саша самый младший, значит он футболист.
5.Миша старше боксера (старше Димы и Саши футболиста) – значит боксер – Дима.
6.Миша – плавание.
Ответ: Миша – плавание, Дима – боксер, Саша – футболист.
![]()
Евклидово расстояние есть длина отрезка прямой, проведённой через две точки, между которыми измеряется расстояние, причём отрезок вот этими двумя точками определяется. Правило, по которому вычисляется расстояние, называется метрикой пространства. В частности, для евклидова пространства это расстояние вычисляется по обычной теореме Пифагора, как корень из суммы квадратов координат вектора, соответствующего отрезку.
Для неевклидовых пространств правило может быть другим, в частности вообще может быть невозможно однозначно измерить расстояние (в пространстве, рассматриваемом в Общей теории относительности).
![]()
Rafail как всегда прав, геометрическая прогрессия с коэффициентом 2 представлена в первом варианте. Но вот мне тяжело представить урожай риса на всей планете, а следовательно убедиться в мощи геометрической прогрессии.
Рассмотрим пример с меньшими цифрами.
Предположим продается пачка сигарет на следующих условиях:
Первая сигарета стоит одну копейку, вторая две, третья четыре, четвертая восемь и так далее. Это есть геометрическая прогрессия в которой первый член равен 1, коэффициент равен 2, а членов ряда 20. Как Вы думаете сколько будет стоить вся пачка? Ну вот так быстро, на вскидку, рублей 10-20. Попробуем посчитать по формуле.
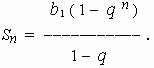
Sn=1*(1-2^20)/(1-2)=1048575 копеек или 10485,75 рублей.
Не хилая такая пачечка получается.
Теперь понятно почему на шахматной доске, где не 20 членов прогрессии, а 64 умещается весь урожай человечества.
![]()
Всем, изучающим математику в школе известно слово “радикал”. или как мы привыкли его называть слово “корень”. Всем известно графическое обозначение радикала (корня) – это ” √ “. И не смотря на то, что перевод с французского – радикальный – это крайний, часто эти два понятия подменяют.
Хотя понятие “коренным образом” подразумевает как бы исследование вопроса досконально и изнутри, а понятие – радикальные меры воспринимаются, как крайние меры, но в математических исследованиях радикал и корень понятия равные.
Наверно потому, что извлечение корня любой степени это радикальное изменение математической величины.
Корень в математике – радикал.
