Как найти длину участка функции - Сайт, где вы сможете решить свои вопросы

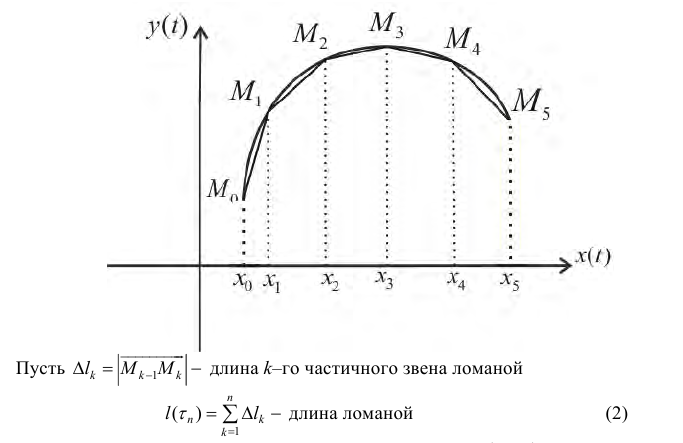
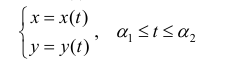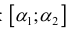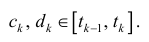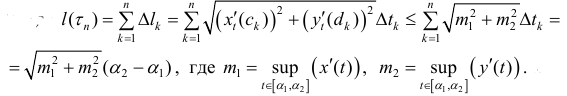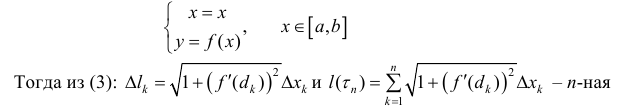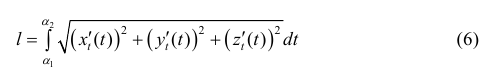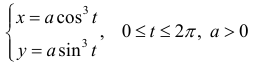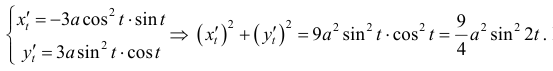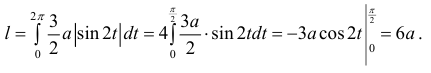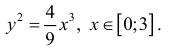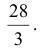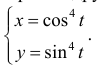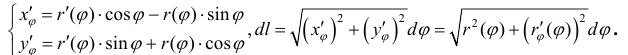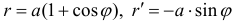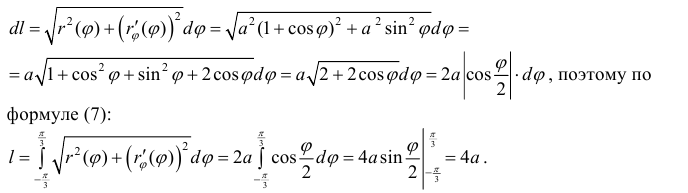Приближение длины дуги эллипса с помощью ломаных

Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой^[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).

Определение[править | править код]

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.

Например, пусть непрерывная кривая gamma в трёхмерном пространстве задана параметрически:

(1)

Приближение кривой ломаными

где , все три функции непрерывны и нет кратных точек, то есть разным значениям соответствуют разные точки кривой. Построим всевозможные разбиения параметрического интервала [a,b] на отрезков: ${displaystyle a=t_{0}<t_{1}<dots <t_{m}=b}$ . Соединение точек кривой ${displaystyle gamma (t_{0}),dots ,gamma (t_{m})}$ отрезками прямых даёт ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных^[2].

Длина дуги циклоиды (s) в зависимости от её параметра (θ)

Связанные определения[править | править код]

Всякая кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая. Снежинка Коха — классический пример ограниченной, но неспрямляемой кривой; более того, любая, сколь угодно малая её дуга неспрямляема^[3].
Параметризация кривой длиной её дуги называется естественной.
Кривая есть частный случай функции из отрезка в пространство. Вариация функции, определяемая в математическом анализе, является обобщением длины кривой (см. ниже).

Свойства[править | править код]

Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна.

В математическом анализе выводится формула для вычисления длины отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

$s=int limits _{a}^{b}{sqrt {{x'}^{2}(t)+{y'}^{2}(t)+{z'}^{2}(t)}},dt$

(2)

Формула подразумевает, что

и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

$s=int limits _{a}^{b}{sqrt {sum limits _{{k=1}}^{n}{f'_{k}}^{2}(t)}},dt$

${displaystyle s=int limits _{a}^{b}{sqrt {1+(f'(x))^{2}}},dx.}$

В полярных координатах

$s=int limits _{a}^{b}{sqrt {r^{2}+left({frac {dr}{dvarphi }}right)^{2}}},dvarphi .$

Формула Крофтона позволяет связать длину кривой на плоскости и интеграл числа её пересечений с прямыми по естественной мере на пространстве прямых.

История[править | править код]

Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»^[4]^[5].

Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина арки циклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.

Вариации и обобщения[править | править код]

Риманово пространство[править | править код]

В n-мерном римановом пространстве с координатами $x^{1}cdots x^{n}$ кривая задаётся параметрическими уравнениями:

$x^{i}=x^{i}(t)qquad qquad$

((3))

Длина кривой в римановом пространстве задаётся формулой:

$s=int limits _{a}^{b}{sqrt {g_{{ij}}{dx^{i} over dt}{dx^{j} over dt}}},dt$

где : $g_{ij}$ — метрический тензор.
Пример: кривая на поверхности в $mathbb {R} ^{3}$ .

Общее метрическое пространство[править | править код]

В более общем случае произвольного метрического пространства (X,rho) длиной кривой называется вариация задающего кривую отображения, то есть длина кривой определяется согласно формуле:

$s=sup sum limits _{{k=0}}^{m}rho (gamma (x_{{k+1}}),gamma (x_{k})),$

где верхняя грань берётся, как и ранее, по всем разбиениям $a=x_{0}<x_{1}<dots <x_{m}=b$ отрезка [a,b] .

См. также[править | править код]

Дифференциальная геометрия кривых
Объём
Определённый интеграл
Площадь
Дуга окружности
Кривая Пеано

Примечания[править | править код]

↑ Длина // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
↑ Шибинский, 2007, с. 199.
↑ Шибинский, 2007, с. 201—202.
↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — С. 49. — 297 с. — (Классики естествознания).
↑ Оригинал цитаты на французском языке: «la proportion qui est entre les droites et les courbes n’étant pas connue, et même, je crois, ne le pouvant être par les hommes», см. Descartes, René. Discours de la méthode…. — 1637. — С. 340.

Литература[править | править код]

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
Мерзон Г. А., Ященко И. В. Длина, площадь, объем. — МЦНМО, 2011. — ISBN 9785940577409.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966.
Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — 543 с. — ISBN 978-5-06-005774-4.

Источник

При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.

Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.

Как вычислить длину кривой

Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).

Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).

Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).

Примеры:

Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

1. Точками х₀= а, х₁…, х_n = b (х₀ < x₁ < …< х_n) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М₀ = А, M₁,…,M_n =В на кривой АВ. Проведем хорды М₀M₁, M₁M₂,…, М_n-1М_n, длины которых обозначим соответственно через ΔL₁, AL₂,…, ΔL_n. Получим ломаную M₀M₁M₂ … M_n-ιM_n, длина которой равна L_n=ΔL₁ + ΔL₂+…+ ΔL_n =

2. Длину хорды (или звена ломаной) ΔL₁ можно найти по теореме Пифагора из треугольника с катетами Δx_i и Δу_i:

По теореме Лагранжа о конечном приращении функции Δу_i=ƒ'(с_i)•Δх_i, где ci є (x_i-1;x_i). Поэтому

а длина всей ломаной M₀M₁… М_n равна

3.Длина l кривой АВ, по определению, равна

Заметим, что при ΔL_i→0 также и Δx_i →0 ΔLi =и, следовательно, |Δx_i|<ΔL_i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx_i→ 0:

Таким образом,или в сокращенной записи l =

Если уравнение кривой АВ задано в параметрической форме

где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,

Пример 2. Определить длину окружности x² + y² = r². Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда,следовательно,

Длина всей окружности L = 2πr.

Пример 3. Найти длину дуги кривой y² = x³ от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x^1/2, откуда

Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).

Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).

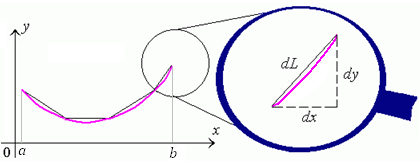
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.

Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:

(1)

где y ‘ – производная функции y = f(x) по переменной x.

Длина дуги равна сумме длин составляющих ее элементов:

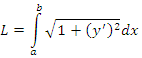Пример 5.

Источник

Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:

В более общем случае, если у нас задана функция

в декартовых координатах и стоит задача найти длину дуги этой кривой между точками

и
,
нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение

означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Длина дуги кривой – определение и вычисление с примерами решения

Длина дуги кривой:

Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде

Разобьем отрезок

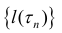
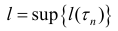
Кривая называется спрямлякмой, если множество – длин всевозможных вписанных в кривую ломаных – ограничено, при этом – называется длиной кривой L.

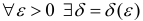
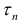
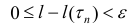
Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если такое, что ∀ разбиения диаметром Δ < δ выполнено неравенство (3)

Теорема 1. Пусть x (t) и y (t) – непрерывно-дифференцируемы, тогда кривая L вида (1) – спрямляемая.
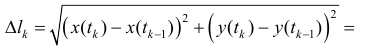
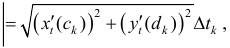
Доказательство. по теореме Лагранжа где
Тогда

Таким образом 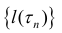– ограничено, и следовательно имеет точную верхнюю грань, что и требовалось доказать.
Найдем длину кривой L. Рассмотрим случай явного задания функции:

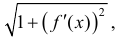
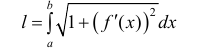
интегральная сумма для функции поэтому:
(4)

Аналогично для кривой L заданной по формулам (1)
(5)

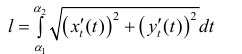
Длина l пространственной кривой L: 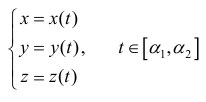находится по формуле:

Пример 1.

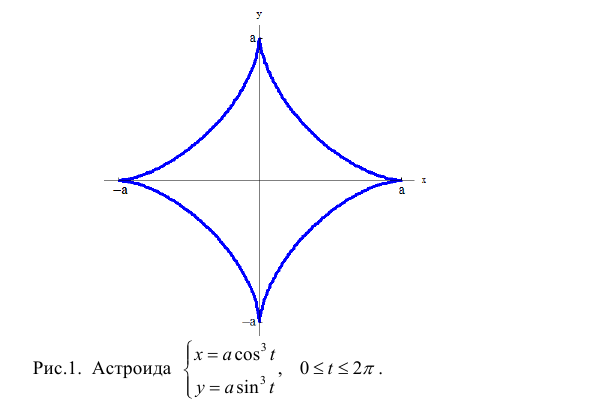
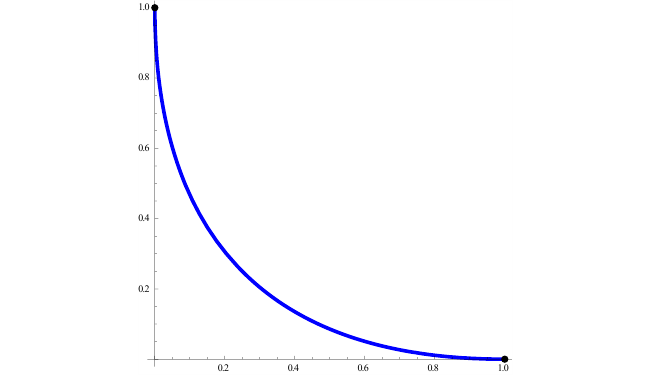
Найдем длину дуги астроиды

Решение.

По формуле (5):

Пример 2.

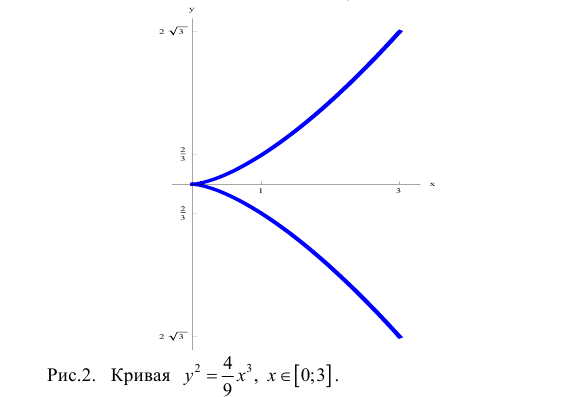
Найти длину дуги линии

Решение.

Кривая симметрична относительно оси Ох:
– задают верхнюю и нижнюю ветви По формуле (4)
Длина всей кривой:

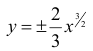
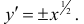
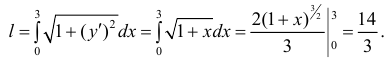
Замечание. Если кривая не является простой, необходимо учитывать возможность самоналожения участков кривой друг на друга.

Пример 3.

Найти длину кривой

Решение.

При 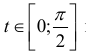получаем график:

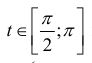
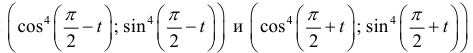
При получаем тот же график, проходимый в обратном направлении (точки совпадают.
Поэтому 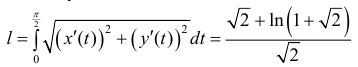(проверить).

Замечание. 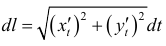называется дифференциалом длины дуги. И тогда формула (5) перепишется в виде:
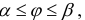
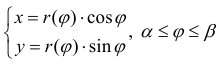
Найдем длину кривой L заданной в полярных координатах: r=r(ϕ), где функция r(ϕ) – непрерывно-дифференцируема. Тогда (см. формулы (1) § 31)
– параметрическое задание кривой;

Поэтому 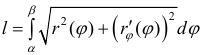(7)

Пример 4.

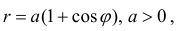
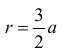
Найти длину дуги части кардиоиды расположенной вне круга
(см. пример 4 § 31).

Решение.

Геометрические фигуры и их свойства
Основные фигуры геометрии и их расположение в пространстве
Пространственные фигуры – виды, изображения, свойства
Взаимное расположения прямых на плоскости
Объем пространственных фигур
Объёмы поверхностей геометрических тел
Фигуры вращения: цилиндр, конус, шар
Объем фигур вращения

Источник

Вычисление
длины дуги кривой в декартовых координатах.Введем понятие длины дуги. Пусть на
плоскости введена кривая, являющаяся
графиком непрерывной функциина отрезке.
Разобьем отрезокточками наnчастей.
Из каждой точкивосстановим перпендикуляр к осиOx;
тогда дугаABразобьется
наnчастей точками(рис.4). Заменим каждый участок дугиучастком прямой.

Определение.Длиной дуги называется пределL,
к которому стремится длина ломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон,
а значит, и при,
т.е.

(8)

Рис. 4 Рис.5

Пусть
функция
и ее производнаянепрерывны на отрезке.
Согласно теореме Пифагора имеем.
Обозначим.
Так каки,
то на основании теоремы Лагранжа получим

Тогда
.
В следствие непрерывности производнойсуществует предел (8) интегральной суммы.
Таким образом,

(9)

По
определению предел (9) равен определенному
интегралу от функции
на отрезке:

.
(10)

Это и
есть формула для вычисления длины дуги.

Пример
4. Найти длину дуги кривой
,
отсеченной прямой(рис.5).

Решение.
Найдем производную функции y=f(x),
заданной неявно соотношением;
имеем,
откудаВ силу симметрии достаточно вычислить
длину половины кривой.
По формуле (10) получим

,
при.

Вычисление
дуги плоской кривой, заданной в
параметрической форме. Рассмотрим
параметрически заданную кривуюгде– непрерывные и имеющие непрерывные
производные функции, причем.
Пусть.
В интеграле (10) произведем подстановку;
так как,
то получим

.
(11)

Пример
5. Найти длину окружности радиуса R.

Решение.
Уравнения окружности в параметрической
форме имеют вид
Найдем четвертую часть длины окружности.
По формуле (11) имеем

Что
согласуется с общеизвестным результатом.

Вычисление
длины дуги плоской кривой в полярных
координатах.Воспользуемся формулами
перехода от полярных координат к
декартовым:(учли,
что радиусrесть функция
полярного угла). Эти уравнения можно
рассматривать, как параметрические
уравнения кривой при изменении параметрав пределах.
Тогда по формуле (11) находим

.
(12)

3. Вычисление объемов и площадей поверхностей вращения.

Пусть
криволинейная трапеция, ограниченная
графиком непрерывной функции y=f(x),
осьюOxи прямымиx=a,x=b, вращается
вокруг осиOx.

(рис.6)

Найдем
объем Vполученного тела
вращения. Ясно, что произвольное
поперечное сечение этого тела представляет
собой круг. Площадь круга, образованного
при сечении тела вращения плоскостьюx=x, есть.
Тогда используя формулу,
получим

(13)

Если
криволинейная трапеция, ограниченная
непрерывной функцией
,
осьюOyи прямымиy=aиy=b, вращается
вокруг осиOy, то объем
полученного тела вычисляется по формуле

(14)

Пример
6. Найти объем конуса с радиусом основания
Rи высотойh.

Решение.
Конус можно считать телом, полученным
вращением прямоугольного треугольника
с катетами hиRотносительно осиOx. Найдем
уравнение гипотенузы этого треугольника.
Имеемy=kx,
где.
По формуле (13) получим

Вычисление
площади поверхности тела вращения.

Определение.Площадью поверхности
тела, полученного при вращении дугиABвокруг осиOxназывается
предел,
к которому стремится площадь поверхности,
образованной вращением вокруг осиOxломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон,
а значит, и при,
т.е..