При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.![1_5254fef39271a5254fef392758[1] 1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png)
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда
,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
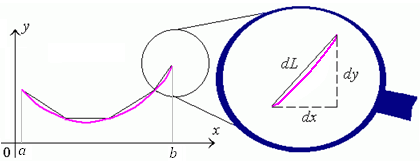
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
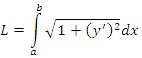 . . |
Пример 5.
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:
В более общем случае, если у нас задана функция
в декартовых координатах и стоит задача найти длину дуги этой кривой между точками
и
,
нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение
означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.

Приближение длины дуги эллипса с помощью ломаных
Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).
Определение[править | править код]
Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных.
Например, пусть непрерывная кривая 

|
(1) |

где 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




Длина дуги циклоиды (s) в зависимости от её параметра (θ)
Связанные определения[править | править код]
- Всякая кривая имеет длину, конечную или бесконечную. Если длина кривой конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая. Снежинка Коха — классический пример ограниченной, но неспрямляемой кривой; более того, любая, сколь угодно малая её дуга неспрямляема[3].
- Параметризация кривой длиной её дуги называется естественной.
- Кривая есть частный случай функции из отрезка в пространство. Вариация функции, определяемая в математическом анализе, является обобщением длины кривой (см. ниже).
Свойства[править | править код]
- Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна.
- В математическом анализе выводится формула для вычисления длины
отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

|
(2) |
- Формула подразумевает, что
и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.
- В n-мерном случае вместо (2) имеем аналогичную формулу:
.
-
- В полярных координатах
:
- Формула Крофтона позволяет связать длину кривой на плоскости и интеграл числа её пересечений с прямыми по естественной мере на пространстве прямых.
История[править | править код]
Задача спрямления оказалась гораздо сложнее, чем вычисление площади, и в античные времена единственное успешное спрямление было выполнено для окружности. Декарт даже высказывал мнение, что «отношение между прямыми и кривыми неизвестно и, даже, думаю, не может быть познано людьми»[4][5].
Первым достижением стало спрямление параболы Нейла (1657), выполненное Ферма и самим Нейлом. Вскоре была найдена длина арки циклоиды (Рен, Гюйгенс). Джеймс Грегори (ещё до открытия математического анализа) создал общую теорию нахождения длины дуги, которая немедленно была использована для различных кривых.
Вариации и обобщения[править | править код]
Риманово пространство[править | править код]
В n-мерном римановом пространстве с координатами 
 , ,
|
((3)) |
Длина кривой в римановом пространстве задаётся формулой:
,
где : 
Пример: кривая на поверхности в 
Общее метрическое пространство[править | править код]
В более общем случае произвольного метрического пространства 

![gamma :[a,b]to X](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc6aa43c7c7048266d04585bb540dc5fcf9caef4)
где верхняя грань берётся, как и ранее, по всем разбиениям 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
См. также[править | править код]
- Дифференциальная геометрия кривых
- Объём
- Определённый интеграл
- Площадь
- Дуга окружности
- Кривая Пеано
Примечания[править | править код]
- ↑ Длина // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ Шибинский, 2007, с. 199.
- ↑ Шибинский, 2007, с. 201—202.
- ↑ Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта / Перевод, примечания и статьи А. П. Юшкевича. — М.—Л.: Гостехиздат, 1938. — С. 49. — 297 с. — (Классики естествознания).
- ↑ Оригинал цитаты на французском языке: «la proportion qui est entre les droites et les courbes n’étant pas connue, et même, je crois, ne le pouvant être par les hommes», см. Descartes, René. Discours de la méthode…. — 1637. — С. 340.
Литература[править | править код]
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
- Мерзон Г. А., Ященко И. В. Длина, площадь, объем. — МЦНМО, 2011. — ISBN 9785940577409.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в трёх томах. — Изд. 6-е. — М.: Наука, 1966.
- Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — 543 с. — ISBN 978-5-06-005774-4.

Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
28
Добавлен:
27.12.2015
Размер:
525.06 Кб
Скачать

Определение 9.1. Кривой в пространстве R3 (или на плоскости R2) называется множество вида
|
` = {P (t) = (x(t); y(t); z(t)) : |
t [α; β]}, |
(11) |
|
где x(t), y(t), z(t) непрерывные функции на [α; β |
]. |
Определение 9.2. Кривая называется гладкой, если существуют непрерывные x˙ = x0(t), y˙ = y0(t), z˙ = z0(t), не обращающиеся в 0 одновременно (при t = α имеют-
ся в виду правые производные, при t = β левые).
Кривая называется кусочно-гладкой, если существуют такие tj :
α = t0 < t1 < . . . < tN = β, что составляющие е кривые {P (t) : t [tj−1; tj]} гладкие.
Определение 9.3. Длина кривой L(`) = супремум длин вписанных в не ломаных
P0P1 . . . Pn, Pi = P (ti), ò. e.
|
L(`) = sup ( |
|Pi−~1Pi| : α = t0 < t1 < . . . < tn = β, n N). |
|
n |
|
|
Xk |
|
|
=1 |
Теорема 9.1. Длина кусочно-гладкой кривой (11) равна
|
β |
|||||
|
L(`) = Z |
dt = L. |
||||
|
x˙ 2 |
+ y˙2 + z˙2 |
(12) |
|||
|
α |
p |
Доказательство. Поскольку при стыковке кривых длины складываются, достаточно доказать теорему для гладкой кривой. Итак, пусть функции x˙ , y˙, z˙ непрерывны на
[α; β]. Они равномерно непрерывны = ε > 0 δ > 0: если s, t [α; β], |s − t| ≤ δ, то |x˙ (s) − x˙ (t)| + |y˙(s) − y˙(t)| + |z˙(s) − z˙(t)| < ε. Возьмем разбиение {ti}ni=0 отрезка
[α; β] с диаметром < δ и построим ломаную P0P1 . . . Pn с концами в узлах разбиения. Оценим е длину:
n
X
L(P0P1 . . . Pn) = |Pi−~1Pi| =
i=1
n
X
p
=(x(ti) − x(ti−1))2 + (y(ti) − y(ti−1))2 + (z(ti) − z(ti−1))2 =
i=1
27

[применим теорему Лагранжа по отдельности к x(t), y(t) è z(t)]
n
X
p
=(ti − ti−1) (x˙ (ξi))2 + (y˙(ηi))2 + (z˙(ζi))2 ≥
i=1
|
[применим неравенство |
√ |
− p |
|||||||||
|
a2 + b2 |
+ c2 |
p2 + q2 + r2 |
≤ |a − p| + |b − q| + |c − r| ] |
||||||||
|
n |
|||||||||||
|
≥ i=1 (ti − ti−1) |
ti |
||||||||||
|
(x˙ (ti))2 |
+ (y˙(ti))2 + (z˙(ti))2 − ε = S{{ti}} − ε(β − α), |
||||||||||
|
X |
p |
||||||||||
|
ãäå |
{ti} |
ïðè |
|||||||||
|
S{ti} является интегральной суммой для интеграла (12) и стремится к L |
|||||||||||
|
δ → 0. Следовательно, L(`) ≥ L. Аналогично доказывается, что |
|||||||||||
|
L(P0P1 . . . Pn) ≤ L + ε |
(13) |
при достаточно малом diam{ti}. Íî åñëè diam{ti} ½недостаточно мал , то в ломаную можно вписать ломаную из более мелких отрезков, длина которой не меньше исходной!
Таким образом, оценка (13) верна для любой ломаной и любого ε > 0 = L(`) =
sup L(P0P1 . . . Pn) ≤ L.
Следствие 9.1. Если плоская кривая является графиком непрерывной функции y = f(x), a ≤ x ≤ b, имеющей кусочно-непрерывную производную, то она кусочно-
гладкая, и е длина равна
|
L{y = f(x), a ≤ x ≤ b} = Z |
b |
|||
|
1 + (f0 |
(x))2 |
dx. |
(14) |
|
|
a |
p |
Доказательство. Подставим в формулу (12) x = t, y = f(t), z = 0.
Следствие 9.2. Если плоская кривая ` задана в полярных координатах: ρ = R(ϕ), α ≤ ϕ ≤ β, и функция R(ϕ) ≥ 0 имеет кусочно-непрерывную производную, то она кусочно-гладкая, и е длина равна
|
β |
|||||||||||
|
L(`) = Z |
|||||||||||
|
R2(ϕ) + (R0 |
(ϕ))2 dϕ. |
(15) |
|||||||||
|
α |
p |
||||||||||
|
Доказательство. Подставим в формулу (12) ϕ = t. Получаем |
|||||||||||
|
y = R(t) sin t |
= |
˙ |
= |
x˙ 2 + y˙2 + z˙2 |
= R2 + R˙ 2. |
||||||
|
y˙ = R˙ sin t + R cos t |
|||||||||||
|
x = R(t) cos t |
x˙ = R cos t − R sin t |
||||||||||
|
z = 0 |
z˙ = 0 |
p |
p |
||||||||
28

Пример 9.1. Найти длину участка графика y = ex îò x = 0 äî x = 1.
По формуле (14) получаем
|
1 |
e |
||||||||||||||||||||||||||||||||||||||||
|
замена |
p |
y |
dy = |
||||||||||||||||||||||||||||||||||||||
|
L = Z0 |
√1 + e2xdx = x = ln y; dx = dy/y = Z1 |
||||||||||||||||||||||||||||||||||||||||
|
y = ex |
1 + y2 |
||||||||||||||||||||||||||||||||||||||||
|
e |
+ y2 |
e |
e |
||||||||||||||||||||||||||||||||||||||
|
1 |
dy |
y dy |
|||||||||||||||||||||||||||||||||||||||
|
= Z1 |
dy = Z1 |
+ Z1 |
= |
||||||||||||||||||||||||||||||||||||||
|
y |
1 + y2 |
y 1 + y2 |
1 + y2 |
||||||||||||||||||||||||||||||||||||||
|
[в первом интеграле |
p |
p, во втором |
p |
2] |
|||||||||||||||||||||||||||||||||||||
|
делаем замену |
z = 1 + y |
||||||||||||||||||||||||||||||||||||||||
|
t = 1/y |
|||||||||||||||||||||||||||||||||||||||||
|
1/e |
1+e2 |
= |
1 |
√t2 |
+ 1 + |
√z 2 |
= |
||||||||||||||||||||||||||||||||||
|
= − Z |
t2 t−1√1 + t−2 + |
Z |
2√z |
Z |
|||||||||||||||||||||||||||||||||||||
|
1 |
· |
dt |
2 |
dz |
1/e |
dt |
1+e2 |
||||||||||||||||||||||||||||||||||
|
√ |
ln(e−1 |
+ √ |
) + √ |
√ |
|||||||||||||||||||||||||||||||||||||
|
= ln(1 + |
2) |
− |
1 + e−2 |
1 + e2 |
− |
2 |
≈ |
2,003. |
|||||||||||||||||||||||||||||||||
Пример 9.2. Найти длину части гиперболической спирали {ρ = ϕ−1}, лежащую в круге {ρ ≤ 1}.
Условию ρ ≤ 1 отвечает ϕ [1; +∞). Рассмотрим участок c ϕ [1; T ]. По формуле (15) получаем
|
T |
T |
p |
T |
T |
||||||||||||||
|
L = Z |
ϕ−2 + ϕ−4dϕ = Z |
ϕ2+ 1 |
dϕ = Z |
1 + ϕ2 + Z |
ϕ2 1 + ϕ2 = |
|||||||||||||
|
ϕ2 |
dϕ |
dϕ |
||||||||||||||||
|
p |
p |
p |
||||||||||||||||
|
1 |
1 |
1 |
1 |
|||||||||||||||
|
[во втором интеграле делаем замену t = 1/ϕ] |
||||||||||||||||||
|
= ln(T + |
1/T |
√1 + t−2 |
1 |
√t2 + 1 |
= |
|||||||||||||
|
√T 2 + 1) − Z |
= ln(T + √T 2 + 1) + Z |
|||||||||||||||||
|
dt |
tdt |
|||||||||||||||||
|
1 |
1/T |
√√ √
|
= ln(T + T 2 + 1) + 2 |
− |
T −2 + 1. Ïðè T |
→ |
+ эта длина неограниченно растет. |
|
∞ |
Oòâåò: +∞.
Поверхности вращения
Пусть поверхность Σ получена вращением вокруг оси Ox гладкой несамопересекающейся кривой ` = {x = x(t), y = y(t), α ≤ t ≤ β}, расположенной в полуплоскости {(x; y) : y ≥ 0}. В этом семестре не буду давать строгое определение площади поверхности. Интуитивно понятно, что площадь Σ равна пределу площадей поверхностей Σ{ti}, полученных вращением ломаных P0P1 . . . Pn, Pi = (x(ti); y(ti)), вокруг оси Ox:
S(Σ{ti}) → S(Σ) ïðè diam{ti} → 0.
29

Найдем площадь поверхности ΣAB, полученной вращением отрезка AB вокруг Ox. Случай 1. yA = yB = боковая поверхность цилиндра, S = 2πyA · |xA − xB|.
Случай 2. yA > yB, xA = xB = êðóã (ïðè yB > 0 с круглой дырой), S = π(yA2 −yB2 ). Случай 3. yA > yB, xA 6= xB = боковая поверхность конуса (при yB > 0 усечен-
| ~ |.
íîãî), S = π(yA + yB) AB
Во всех трех случаях верна формула:
p
S(ΣAB) = π(yA + yB) (xA − xB)2 + (yA − yB)2.
Следовательно, площадь поверхности Σ{ti} равна
n
S(Σ{ti}) = 2π X y(ti−1)2+ y(ti)p(x(ti) − x(ti−1))2 + (y(ti) − y(ti−1))2 =
|
i=1 |
||||
|
n |
||||
|
Xi |
p |
[θi, ξi, ηi (ti−1; ti)], |
||
|
= 2π |
y(θi) (x˙ (ξi))2 + (y˙(ηi))2 (ti − ti−1) |
|||
|
=1 |
÷òî ïðè diam{ti} → 0 стремится к
|
β |
||||||
|
S(Σ) = 2π Z |
||||||
|
y(t) |
x˙ 2 |
+ y˙2 |
dt. |
(16) |
||
|
α |
p |
Следствие 9.3. Если плоская кривая является графиком непрерывной функции y = f(x) ≥ 0, a ≤ x ≤ b, имеющей непрерывную производную, то площадь поверхности, полученной вращением е вокруг Ox, равна
|
= f(x)} = 2π Z |
b |
||||||
|
S{a ≤ x ≤ b; |
|||||||
|
y2 + z2 |
f(x) |
1 + (f0 |
(x))2 |
dx. |
|||
|
p |
a |
p |
Если же (при a ≥ 0) вращать ту же кривую вокруг Oy, то получим площадь
|
S{a ≤ ρ = √ |
≤ b; y = f(ρ)} = 2π Z |
b |
|||||
|
x2 + z2 |
x |
1 + (f0 |
(x))2 |
dx. |
|||
|
a |
p |
30

Доказательство. Подставим в формулу (16) x = t, y = f(t). Только во втором случае x è y в ней поменяются ролями.
Следствие 9.4. Если плоская кривая задана в полярных координатах: ρ = R(ϕ), 0 ≤ α ≤ ϕ ≤ β ≤ π, и функция R(ϕ) ≥ 0 имеет непрерывную производную, то площадь поверхности Σ, полученной вращением е вокруг Ox, равна
|
β |
|||||
|
S(Σ) = 2π Z |
|||||
|
R(ϕ) sin ϕ |
R2 |
(ϕ) + (R0(ϕ))2 |
dϕ. |
||
|
α |
p |
Доказательство. Подставим в (16) ϕ = t = x = R(t) cos t, y = R(t) sin t ≥ 0.
Пример 9.3. Длина дуги ` гиперболы y = 1/x, 1 ≤ x ≤ b, выражается неберущимся
Zb √
интегралом L(`) = 1 + x−4 dx.
1
Если же мы будем вычислять площадь поверхности Σ, полученной вращением ` вокруг оси Ox, то сможем выразить интеграл аналитически:
|
S(Σ) = 2π Z1 |
b |
√1 + x−4 |
dx = |
|
|
x |
||||
|
1 |
|
[подстановкa u = √ |
= x = (u2 |
1)−1/4; dx = |
1 (u2 |
1)−5/4udu] |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 + x−4 |
− |
− |
− |
||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
√ |
√ |
√ |
|||||||||||||||||||||||||||||||||||||||||||||||
|
1+b−4 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
π |
(u2 |
1)41 −45 u2du = π |
u2 |
du = |
π |
2u + ln |
u − 1 |
√ |
= |
|||||||||||||||||||||||||||||||||||||||
|
− |
Z |
− |
Z |
u2 |
1 |
2 |
u + 1 |
||||||||||||||||||||||||||||||||||||||||||
|
1+b−4 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
√2 |
√1+b− |
4 |
− |
||||||||||||||||||||||||||||||||||||||||||||||
|
+ 1! |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
√2 + 1 |
− |
− |
− |
√1 + b−4 |
||||||||||||||||||||||||||||||||||||||||||||
|
= |
π |
2√ |
2 |
+ ln |
√2 − 1 |
2√ |
1 + b |
4 |
ln |
√1 + b−4 |
− 1 |
||||||||||||||||||||||||||||||||||||||
31

10 Физические приложения определенных интегралов
Определенный интеграл позволяет вычислить полное значение аддитивной скалярной физической величины1, если известна плотность е распределения (линейная, поверхностная или объемная), и эта плотность зависит лишь от одной координаты.
1. Кусочно-гладкая кривая ` = {(x(t); y(t); z(t)) : t [α; β]}, на которой аддитивная
величина M имеет линейную плотность распределения τ(t). Полное значение M и среднее значение τ (средняя линейная плотность) вычисляются так:
|
β |
τ(t) (x0(t))2 + (y0(t))2 + (z0(t))2 dt; τ = L((`)). |
(17) |
|||||
|
M(`) = Z |
|||||||
|
M ` |
|||||||
|
α |
p |
Пример 10.1. С какой силой ~
F масса 1 кг в точке O(0; 0; 0) притягивается стержнем {x = b; z = 0; |y| ≤ a} с постоянной линейной плотностью τ(кг/м)?
Из симметрии Fy = Fz = 0. Масса m в точке P (x; y; z) притягивает O с силой
|
Gm |
~ |
Gτ |
|||||||||||||||||||
|
OP . Следовательно, плотность распределения искомой Fx равна |
b. |
||||||||||||||||||||
|
~ |
3 |
(b |
2 |
2 |
) |
3/2 |
|||||||||||||||
|
|OP | |
+ y |
||||||||||||||||||||
|
Таким образом, |
|||||||||||||||||||||
|
a |
(b2 + y2)3/2 |
= |
y = b tg t; dy = cos2 t |
= |
|||||||||||||||||
|
Fx = Gτb Z |
|||||||||||||||||||||
|
dy |
h |
b dt |
i |
||||||||||||||||||
|
−a |
|||||||||||||||||||||
|
= Gτb |
arctg(a/b) |
= |
b |
· 2 sin arctg b |
= b√b2 |
+ a2 |
|||||||||||||||
|
Z |
b2 |
||||||||||||||||||||
|
cos t dt |
Gτ |
a |
2a G τ |
−arctg(a/b)
2.Плоская пластина. Если пластина Π имеет вид {a ≤ x ≤ y; f(x) ≤ y ≤ g(x)}, g(x) ≥ f(x) кусочно-непрерывны, и величина M имеет поверхностную плотность
1Такими величинами являются: масса; заряд; энергия (потенциальная, кинетическая, тепловая); статический момент; момент инерции; время движения; одна из компонент силы, действующей на тело (давление, притяжение) или вызываемой этим телом; момент такой силы.
32

распределения σ(x), то полное значение M и среднее значение σ вычисляются так:
|
M(Π) = Za |
b |
σ = S(Π) . |
(18) |
|
|
(g(x) − f(x))σ(x)dx; |
||||
|
M(Π) |
||||
|
3. Трехмерное тело. Пусть B кубируемое тело, |
a = min x, b = max x, Bx |
|||
|
B |
B |
сечения B плоскостями, параллельными Oyz; величина M имеет пространственную
|
плотность распределения γ(x). Тогда полное значение M и среднее значение γ вычис- |
|||||||||
|
ляются так: |
b |
||||||||
|
M(B) = Za |
γ = V (B) . |
(19) |
|||||||
|
S(Bx)γ(x)dx; |
|||||||||
|
M(B) |
|||||||||
|
Пример 10.2. За какое время вода вытечет из конической воронки высоты H |
|||||||||
|
и радиуса R, если скорость вытекания = C |
√ |
(ì3/c); z глубина, C заданная |
|||||||
|
z |
|||||||||
|
константа? Представим воронку в виде |
; 0 ≤ z ≤ H . |
||||||||
|
B = px2 + y2 ≤ H |
|||||||||
|
Rz |
Время вытекания воды T имеет пространственную плотность γ = (C√z)−1. Ïî формуле (19) получаем:
|
H |
H |
πR2z2 |
πR2 |
H |
πR2√ |
|||||||
|
S B |
2 |
H |
||||||||||
|
T = Z0 |
C(√ |
z) |
dz = Z0 |
H2 · C√ |
dz = |
Z0 |
z3/2dz = |
|||||
|
H2 · C |
5C |
|||||||||||
|
z |
z |
Моменты и центр масс
Если известна плотность распределения массы % (линейная, поверхностная или
объемная), то статические моменты и моменты инерции имеют соответствующие плотности распределения:
Mx My
x · % y · %
(y2 + z2)% (x2 + z2)%
Если получается плотность, зависящая от одной координаты, то момент можно вычислить через интеграл. Центр масс имеет координаты xc = Mx/M, yc = My/M, zc =
Mz/M.
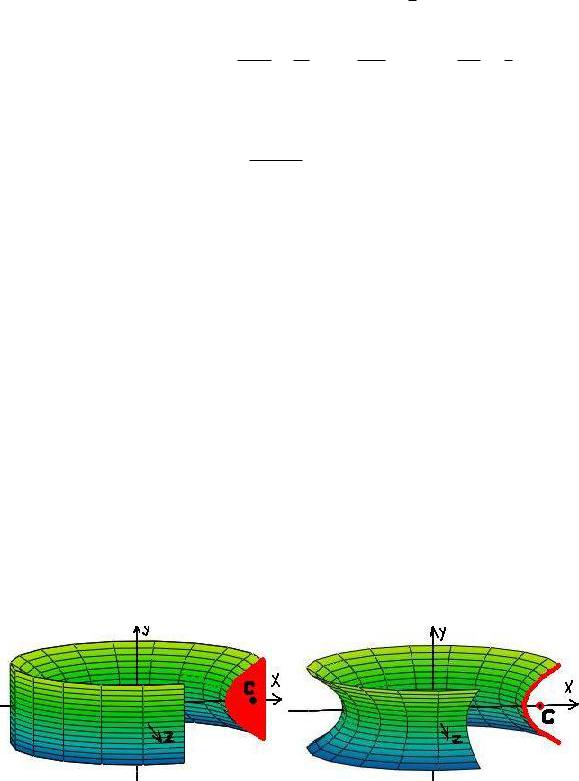
Пример 10.3. Найти центр масс полушарà ïîñòоянной√ плотности. p
Представим полушар в виде 0 ≤ x ≤ R, y2 + z2 ≤ R2 − x2. Будем считать, что плотность = 1 (результат от не не зависит). Из симметрии очевидно, что yc = zc = 0. Bычислим массу M и статический момент Mx:
33
|
R |
||||||||||||
|
M = π Z (R2 − x2)dx = π R2x − |
x3 |
R |
||||||||||
|
3 |
0 |
|||||||||||
|
0 |
||||||||||||
|
R |
||||||||||||
|
Mx = π Z |
(R2 − x2)x dx = π |
2 2 |
4 |
R |
= |
4 |
||||||
|
2 |
− 4 |
0 |
4 |
|||||||||
|
0 |
R x |
x |
πR |
|||||||||
= 23πR3;
= xc = MMx = 38R.
Ответ: C(3R/8; 0; 0).
Пример 10.4. Найти момент инерции круглой пластины радиуса R и постоянной плотности 1кг/м2 относительно e √диаметра.
|
Представим пластину в виде |
{| |
y |
| ≤ |
R2 |
2 |
} |
Oxy и выберем диаметр, лежащий |
|||||||||||||||
|
− x |
2 |
+ z |
2 |
= x |
2. По формуле (18) |
|||||||||||||||||
|
на оси Oy. Плотность распределения JOy равна x |
||||||||||||||||||||||
|
R |
||||||||||||||||||||||
|
JOy = Z |
2√ |
x2dx = |
||||||||||||||||||||
|
R2 − x2 |
[подстановка x = R sin t] |
|||||||||||||||||||||
|
−R |
||||||||||||||||||||||
|
π/2 |
π/2 |
|||||||||||||||||||||
|
= |
Z |
2R4 cos2 t sin2 t dt = |
R4 |
Z |
sin2 |
2t dt = |
πR4 |
(êã · ì2). |
||||||||||||||
|
2 |
4 |
|||||||||||||||||||||
|
−π/2 |
−π/2 |
|||||||||||||||||||||
|
Следующие две |
теоремы Гульдена |
бывают полезны при вычислении объемов тел |
||||||||||||||||||||
|
вращения и площадей поверхностей вращения. |
Теорема 10.1. Объем тела B, полученного вращением вокруг оси Oy квадрируемой фигуры Φ, расположенной в полуплоскости {(x; y) : x ≥ 0}, равен V (B) = 2πS(Φ)xc, где C центр масс Φ, если е поверхностная плотность ≡ 1.
Доказательство. Äëÿ Φ = {a ≤ x ≤ b; f(x) ≤ y ≤ g(x)} получим
|
S(Φ)xc = Mx(Φ) = Za |
b |
2π . |
|
x(g(x) − f(x))dx = |
||
|
V (B) |
Если же Φ склеена из нескольких фигур такого вида, то и статические моменты, и объемы сложатся. 
34
Соседние файлы в папке Лекции, матан
- #
- #
Преподаватель который помогает студентам и школьникам в учёбе.
Длина дуги кривой – определение и вычисление с примерами решения
Длина дуги кривой:
Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде
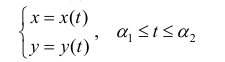
Разобьем отрезок 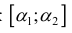
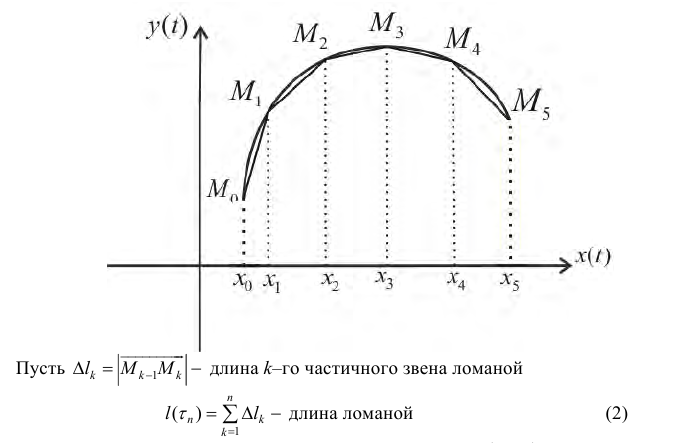
Кривая называется спрямлякмой, если множество  – длин всевозможных вписанных в кривую ломаных – ограничено, при этом
– длин всевозможных вписанных в кривую ломаных – ограничено, при этом  – называется длиной кривой L.
– называется длиной кривой L.
Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если 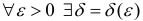 такое, что ∀ разбиения
такое, что ∀ разбиения 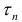 диаметром Δ < δ выполнено неравенство
диаметром Δ < δ выполнено неравенство 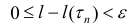 (3)
(3)
Теорема 1. Пусть x (t) и y (t) – непрерывно-дифференцируемы, тогда кривая L вида (1) – спрямляемая.
Доказательство. 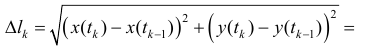 по теореме Лагранжа
по теореме Лагранжа 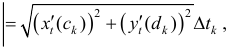 где
где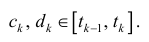
Тогда 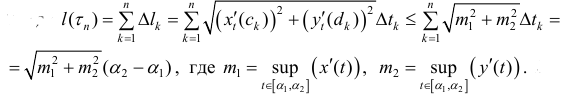
Таким образом 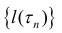 – ограничено, и следовательно имеет точную верхнюю грань, что и требовалось доказать.
– ограничено, и следовательно имеет точную верхнюю грань, что и требовалось доказать.
Найдем длину кривой L. Рассмотрим случай явного задания функции:
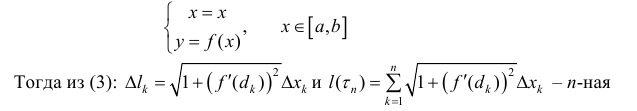
интегральная сумма для функции 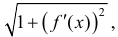 поэтому:
поэтому:
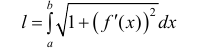 (4)
(4)
Аналогично для кривой L заданной по формулам (1)
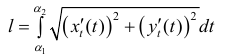 (5)
(5)
Длина l пространственной кривой L: 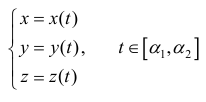 находится по формуле:
находится по формуле:
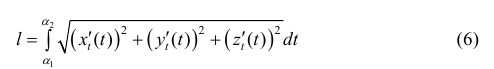
Пример 1.
Найдем длину дуги астроиды 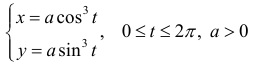
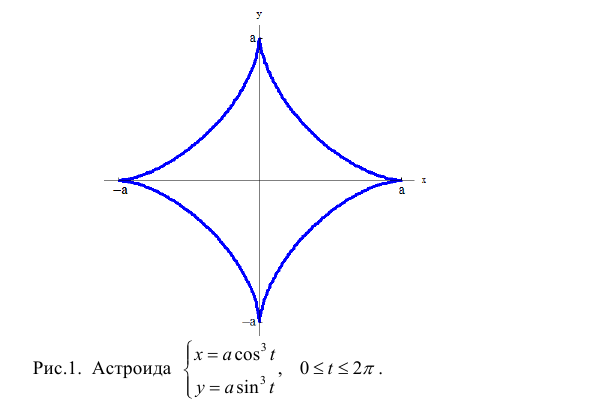
Решение.
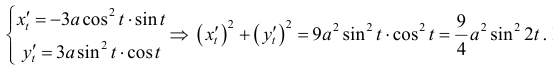
По формуле (5): 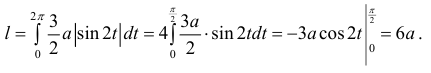
Пример 2.
Найти длину дуги линии 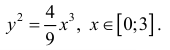
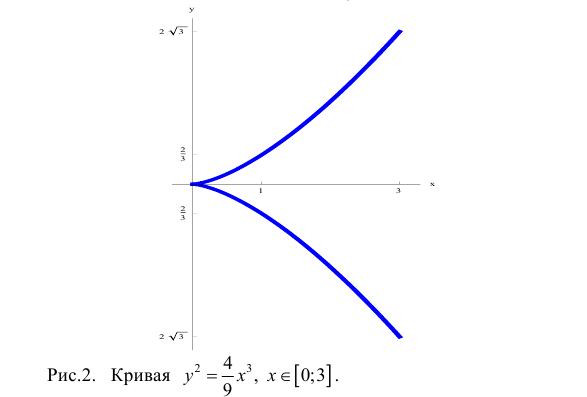
Решение.
Кривая симметрична относительно оси Ох:
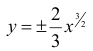 – задают верхнюю и нижнюю ветви
– задают верхнюю и нижнюю ветви 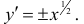 По формуле (4)
По формуле (4)
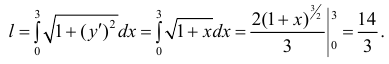 Длина всей кривой:
Длина всей кривой: 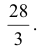
Замечание. Если кривая не является простой, необходимо учитывать возможность самоналожения участков кривой друг на друга.
Пример 3.
Найти длину кривой 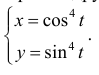
Решение.
При 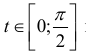 получаем график:
получаем график:
При 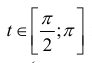 получаем тот же график, проходимый в обратном направлении (точки
получаем тот же график, проходимый в обратном направлении (точки 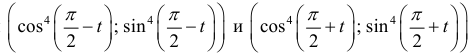 совпадают.
совпадают.
Поэтому 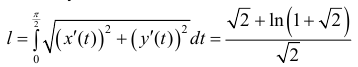 (проверить).
(проверить).
Замечание. 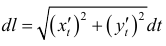 называется дифференциалом длины дуги. И тогда формула (5) перепишется в виде:
называется дифференциалом длины дуги. И тогда формула (5) перепишется в виде:
Найдем длину кривой L заданной в полярных координатах: r=r(ϕ), 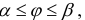 где функция r(ϕ) – непрерывно-дифференцируема. Тогда (см. формулы (1) § 31)
где функция r(ϕ) – непрерывно-дифференцируема. Тогда (см. формулы (1) § 31)
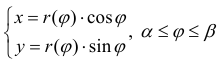 – параметрическое задание кривой;
– параметрическое задание кривой;
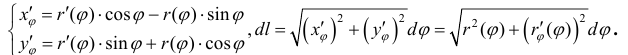
Поэтому 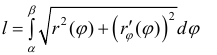 (7)
(7)
Пример 4.
Найти длину дуги части кардиоиды 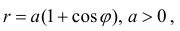 расположенной вне круга
расположенной вне круга
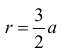 (см. пример 4 § 31).
(см. пример 4 § 31).
Решение.
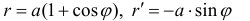
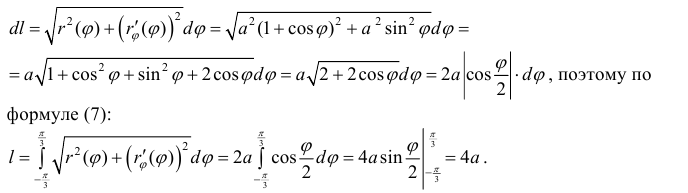
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры – виды, изображения, свойства
- Взаимное расположения прямых на плоскости
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения




