Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория – форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) – в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 – t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость – векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ – средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Как найти длину пути
Отправляясь в поход, лучше заранее найти длину пути, который вам предстоит пройти. Если путешествие автомобильное, то зная протяженность дороги, можно рассчитать количество топлива. Пешим туристам длина маршрута понадобится для оценки времени и запасов продовольствия. Даже отправляясь в гости, желательно поточнее определить длину пути, чтобы не оказаться в положении нежданного гостя.

Вам понадобится
- – линейка;
- – циркуль;
- – крупномасштабная карта;
- – курвиметр;
- – полоска бумаги.
Инструкция
Чтобы найти длину предполагаемого или пройденного пути, возьмите крупномасштабную карту и начертите на ней весь маршрут. Чтобы получить более точные результаты, пройденный путь лучше отмечать во время путешествия, а не после него. Если поездка состоялась на автомобиле, то восстановить траекторию можно на основе отмеченных на карте дорог. Однако, если во время путешествия случались возвраты, объезды или передвижения по проселочным (грунтовым) дорогам, то обозначить пройденный путь будет довольно-таки затруднительно.
Если маршрут начерчен ориентировочно или не требуется большая точность измерений, то можно обойтись лишь циркулем и линейкой. Для этого возьмите циркуль, раздвиньте его ножки на один сантиметр и «пройдитесь» им по отмеченному на карте маршруту. Затем умножьте количество «шагов» циркуля на масштаб карты (количество километров в одном сантиметре) – получится длина пути в километрах. Последний участок маршрута измерьте линейкой, переведите миллиметры в сантиметры и также умножьте на масштаб карты. После чего прибавьте длину этого участка к длине пути, измеренной с помощью циркуля.
Если маршрут пришлось чертить на мелкомасштабной карте или дорога была очень извилистой, то расстояние между ножками циркуля выберите равным 0,5 см. В этом случае, при расчете длины пути, количество шагов циркуля предварительно разделите на два.
Если же, наоборот, карта оказалась крупномасштабной (топографической) или маршрут был достаточно прямолинейным (автомобильная или железная дорога), то зафиксируйте расстояние между ножками циркуля равным нескольким сантиметрам. Это позволит ускорить измерения и не ошибиться при подсчете шагов циркуля. При окончательном расчете длины пути не забудьте умножить количество шагов на расстояние (количество сантиметров) между иголками циркуля.
Если в маршруте встречаются очень извилистые участки (русла рек, осмотр достопримечательностей), то для более точного измерения их длины возьмите полоску тонкой бумаги. Поставьте ее на ребро и проложите вдоль всего маршрута. Затем измерьте длину полоски с помощью линейки. Этот способ измерения длины пути желательно комбинировать с вышеописанными, так как он пригоден лишь для небольших участков.
Чтобы получить наиболее точные результаты измерений, возьмите прибор, называемый курвиметром. Он представляет из себя колесико и счетчик его оборотов. Так как длина окружности колесика и масштаб карты известны, то просто перемножьте число оборотов, периметр колесика (в сантиметрах) и масштаб (количество километров в одном сантиметре). Профессиональный курвиметр произведет все расчеты автоматически – просто сообщите ему масштаб и «прокатитесь» по отмеченному на карте маршруту.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
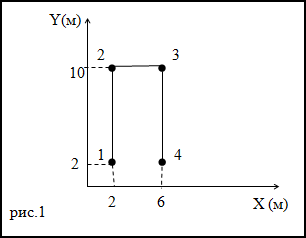
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
Траектория – это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, – криволинейным (с).
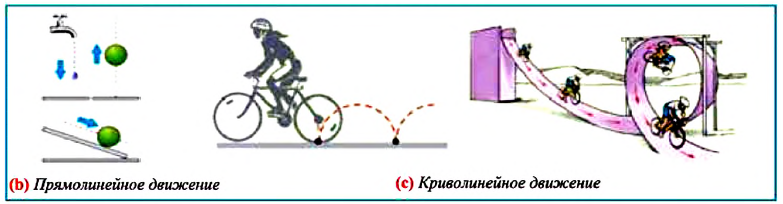
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой 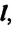
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 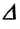 (буква греч. алфавита) перед этой величиной.
(буква греч. алфавита) перед этой величиной.
Изменение координат материальной точки во время движения
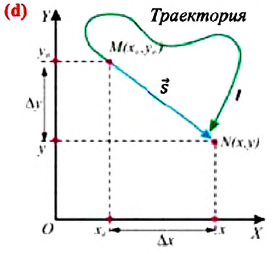
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается 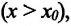 то изменение координаты по этой оси будет положительным:
то изменение координаты по этой оси будет положительным: 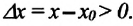 Координата же муравья по оси У уменьшается
Координата же муравья по оси У уменьшается 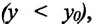 поэтому изменение его координаты по этой оси будет отрицательным:
поэтому изменение его координаты по этой оси будет отрицательным: 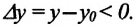
Изменение радиус-вектора материальной точки во время движения
На следующем рисунке представлены радиус-векторы 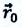 и
и 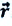 начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор
начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор 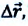 соединяющий концы этих радиус-векторов
соединяющий концы этих радиус-векторов 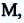 называют перемещением данной материальной точки за промежуток времени
называют перемещением данной материальной точки за промежуток времени 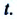 Согласно правилу сложения векторов:
Согласно правилу сложения векторов:  Из последнего выражения получается,
Из последнего выражения получается, 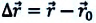 или
или 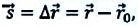 где
где  — перемещение материальной точки.
— перемещение материальной точки.
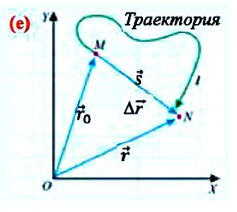
Перемещение – это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина – это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами – сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
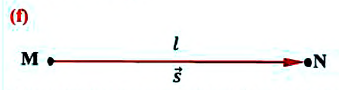
Материальная точка прошла расстояние 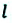 от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения:
от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения: 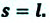

Материальная точка прошла расстояние 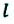 от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку
от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку 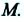 В этом случае материальная точка прошла путь, равный
В этом случае материальная точка прошла путь, равный 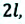 а модуль перемещения равен нулю:
а модуль перемещения равен нулю:

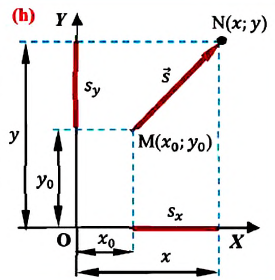
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 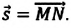 Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения
Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения 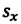 и
и 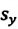 (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
(h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
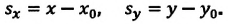
Одинаковы ли путь и перемещение
Задача:
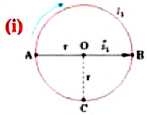
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
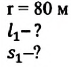
Решение:
Пройденный путь 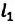 равен длине дуги:
равен длине дуги: 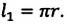
Модуль перемещения же равен диаметру окружности: 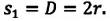
Вычисление:
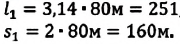
Что такое путь и перемещение
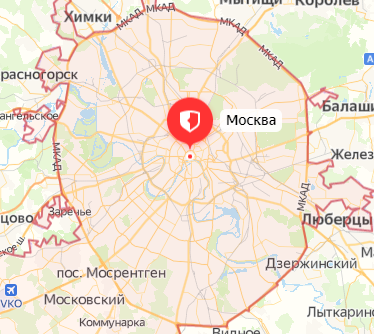
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь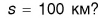
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
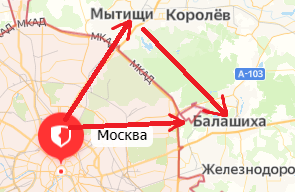
Обозначим перемещение символом 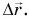 На рисунке 38 вектор
На рисунке 38 вектор 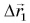 — это перемещение автобуса из Минска в Мытищи, вектор
— это перемещение автобуса из Минска в Мытищи, вектор 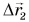 — из Мытищь в Балашиху, а вектор
— из Мытищь в Балашиху, а вектор  — из Минска в Борисов.
— из Минска в Борисов.
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 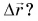 Нельзя, поскольку путь S — скаляр, а перемещение
Нельзя, поскольку путь S — скаляр, а перемещение 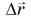 — вектор.
— вектор.
Сравнивать путь S можно с модулем перемещения 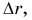 который является скалярной величиной. Равен ли путь модулю перемещения?
который является скалярной величиной. Равен ли путь модулю перемещения?
В рассматриваемом примере путь, пройденный автобусом за два часа, 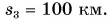 Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова:
Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: 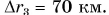 Путь автобуса больше модуля его перемещения:
Путь автобуса больше модуля его перемещения: 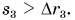
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
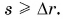
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
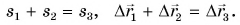
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 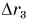 сумме модулей
сумме модулей 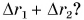 Ответьте самостоятельно.
Ответьте самостоятельно.
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
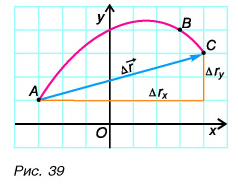
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 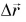 на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
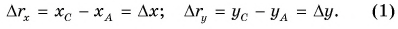
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
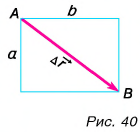

Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
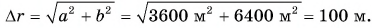
Путь конькобежца: 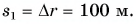
Путь пешехода: 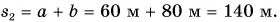
Ответ: 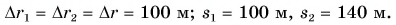
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).

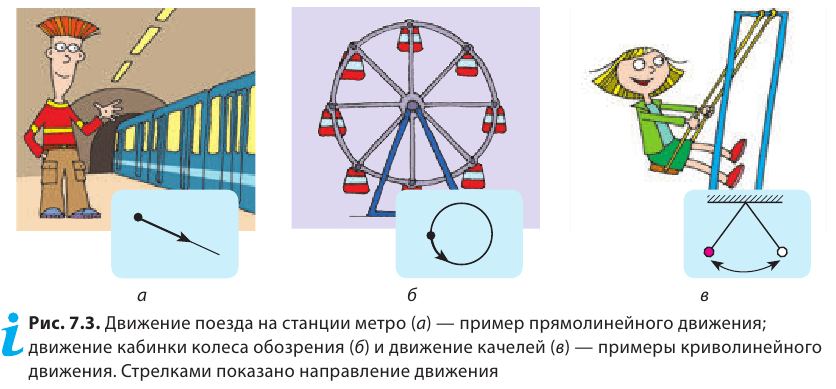
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
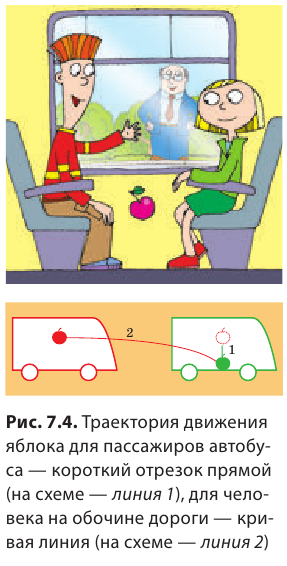
Чем путь отличается от перемещения
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
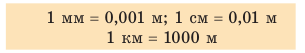
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
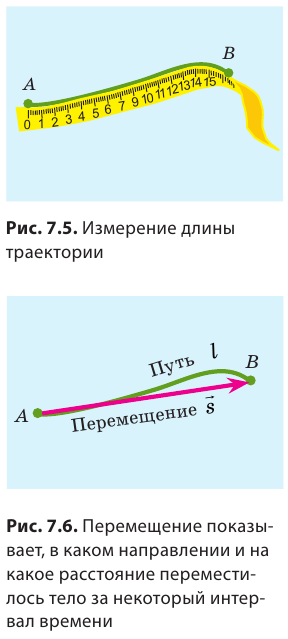
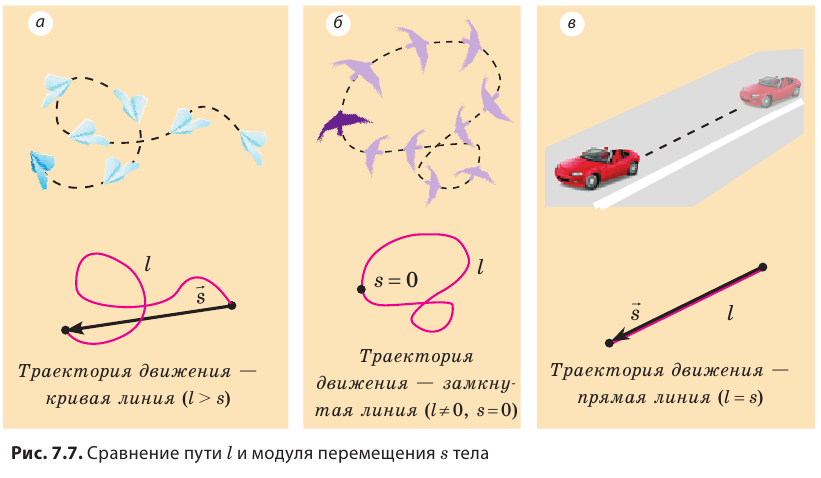
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 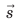 . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
. Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 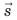 — это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
— это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось

Количество Ваших материалов: 0. Авторскоесвидетельство о публикации в СМИ Свидетельство
о создании электронного портфолио Грамота за
информатизацию образования Рецензия
на любой материал бесплатно Видеоуроки
по быстрому созданию эффектных презентаций
Технологическая карта урока Класс:3Предмет: математикаУМК: «Планета знаний», учебник «Математика» М.И. Башмаков, М.Г.Нефёдова 3 класс, ч.1, стр.106107Тема урока: Вычисление длины пути.Тип урока: изучения и первичного закрепления знанийМетоды: наглядный, словесный, диалог, частичнопоисковый.Формы организации деятельности учащихся: фронтальная, групповая, индивидуальная (самостоятельная работа).Урок построен с использованием информационнокоммуникативной технологии на основе технологии деятельностного подхода.Оборудование: учебник «Математика» 3 кл. Ч.1 М.И. Башмаков,М.Г. Нефедова, М.Г.Нефёдова стр.106107, мультимедийная презентация, , карточки с заданиями для самостоятельной работы . Цель урока: учить вычислять длину пути; совершенствовать умения располагать единицы измерения пути в порядке возрастания; повторение единиц измерения длины (сантиметр, метр, дециметр, километр); формирование умений решать текстовые задачи, содержащие единицы измерения длиныЗадачи: Образовательные: повторить единицы измерения пути, учить решать задачи на нахождение расстояния (пути), продолжать учить записывать краткую запись задач; сравнивать единицы измерения; совершенствовать вычислительные навыки (устные приемы вычислений в пределах 1000); расширять математический кругозор учащихся. Метапредметные: формирование универсальных учебных действий (УУД).Личностные: развивать учебнопознавательный интерес к учебному материалу и способам решения задач; формирование ценностносмысловой ориентации учащихся в содержании учебного материала, в социальных ролях и межличностных отношениях, формирование личностных универсальных учебных действий. Регулятивные: принимать и сохранять учебную задачу; планировать свои действия в соответствии с поставленной задачей; оценивать правильность выполнения действия; адекватно воспринимать предложения сверстников и учителя. Познавательные: развивать познавательную активность, умение наблюдать, анализировать, делать выводы, умение устанавливать связи между единицами измерения (см, м, км), развивать внимание, наблюдательность осуществлять работу с графической информацией (бланк с заданием в табличной форме); обнаруживать пробелы в информации; владеть рядом общих приёмов решения задач.
Коммуникативные: строить монологическое высказывание, владеть диалогической формой коммуникации; формировать умения учебного сотрудничества через работу в паре, в группе.Этап урока (цельэтапа)Ι. Мотивация кучебной деятельности.Цель: включениеучащихся вдеятельность наличностном уровне.Технологическая карта урокаДеятельность учителяДеятельность учащихсяУУДКоммуникативныеУУДуметь совместнодоговариваться оправилах поведенияи общения на урокахи следовать им.Начинаем наш урок математики. а) Создание положительного эмоционального настроя: слайд1 Прозвенел уже звонок, начинается урок. Пожимают друг другу руки ижелают успешной работы науроке.Математику, друзья.Нам не знать икак нельзя!Считать мы будем, рассуждать, Стараться знать ее на 5!б) Мотивация Сегодня мы совершим очередное путешествие в мирматематики. В какую область отправимся? (Какой разделизучаем?) Числа и величины. Нам предстоит серьезная работа, в ходе которой вы получитемного новой информации.Что такое информация и откуда мы ее можем получить?Что такое математическая информация?Информация – это то, что мыслышим, видим, чувствуем. Она
.ΙΙ Актуализациязнаний и фиксациязатруднения впробном учебномдействии.Цель: повторениематериала,необходимого для«открытия новогознания», и выявлениезатруднений виндивидуальнойдеятельностиучащихся. к нам приходит с помощью 5органовчувств.Математическая информация –это новый материал, которыймы получаем на урокематематики в виде примеров,задач, схем, чертежей и другого.Устно объясняют 6дм2см<63см7дм6см>67см81см<8дм2см3дм4см<43см7*2<.7+7+72*9>8*212*2>10+1012:2<122(2м3дм4см+3м1дм6см)4м2дм3см=1м2дм7смосталосьтесьмыПознавательныеУУДобобщениеанализ, синтез, выбор оснований длясравненийДля работы на уроке нам нужно повторить единицы измерениядлины:Сравните:>, <, или =6дм2см…63см7дм6см…67см81см…8дм2см3дм4см….43см782….7+7+72*9…8*212*2…10+1012:2…122Решите задачи.У Насти было два куска синей тесьмы. Длина первого куска2м3дм4см, а длина второго3м1дм6см. Для отделки фартука онаизрасходовала 4м2дм3см этой тесьмы. Сколько тесьмы у неёосталось?Незнайка начертил первый отрезок длиной 6 см, а второй в 4 разадлиннее. Какой длины получился второй отрезок? 6*4=24(см)длинаотрезка второго

Выявление места ипричинызатруднения.Цель: обсуждениезатруднений,проговаривание целиурока в виде вопроса,на который предстоитответить.Посмотрите на доску Что за герои у нас в гостях? Незнайка,Винтик, доктор Пилюлькин, Знайка,Тюбик.(картинки) Ребята,Незнайка отправился в гости к Знайке. Посмотрите схему егодвиженияпо дороге он зашёл к Винтику, Тюбику и докторуПилюлькину. Как найти длину пути Незнайки?Можем найти? А чего 180? Почему не можем узнать длину пути?! Какие единицы измерения длины вы знаете? А в каких единицах на данном рисунке можно измерить длинупути? Мы утром идём в школу. В каких единицах мы можем измеритьрасстояние от дома до школы? А расстояние от нашего города до Москвы? А расстояние от Земли до Луны? У кого есть дома черепашка? Что можно про неё сказать?. А путь, который проползёт черепашка за 1 минуту в чём можемизмерить? Мы подпишем единицы длины пути, можем найти расстояние,которое пройдёт Незнайка? Да, надо сложить все известныечисла..Не знаем. Т. к. не указаныединицы измерения пути. Незнаем в чём измерять! (мм, см, дм, м, км)В метрах. В метрахВ более крупных единицах вкилометрах. В километрах.Очень медленно передвигаетсяЛичностные УУД проявить учебнопознавательныйинтерес к новомуматериалу.Регулятивные УУДуметь высказыватьсвоё предположение.КоммуникативныеУУДучастие вколлективномобсуждениипроблемы;умение оформлятьсвои мысли в устнойформе.
Предположите, какая тема нашего урока? Сформулируйте цель урока.(Слайд4)Какие цели поставим перед собой?(Слайд5)В см или дм да Сегодня на уроке, я буду учиться вычислять длину пути.повторить единицы измерения длины, сравнивать их научиться вычислять длину путиПознавательныеУУД анализировать,синтезировать,сравниватьинформацию.Регулятивные УУДпроявлятьпознавательнуюинициативу вучебномсотрудничестве.Откройте учебник на с.106, з.2. Прочитайте задачу.О чём говорится в задаче? На каких видах транспорта?Запишем кратко (на доске) и в тетрадяхКакие главные слова? На чём путешествовали? Что значит втрое?Третьеклассники отправились впоход.На автобусе, на поезде, пешком,на лодке Автобус, поезд, пешком, лодка.На автобусе40км.На поезде? км. на 240 км б.Пешком? км. В 7 раз м.На лодке? км. в з раза б. ПознавательныеУУДсамостоятельноесоздание способоврешения проблемныхзадач.Регулятивные УУД саморегуляцияКоммуникативныеУУДПостроение проектавыхода иззатрудненияЦель: обсуждениезатруднений,проговаривание целиурока в виде вопроса,на который предстоитответить.III. Реализацияпостроенного проекта.Цель: учить применять полученные знания при решении текстовых задач.
Какой вопрос задачи?Можем ответить сразу? Можем узнать сколько прошли пешком? Можем узнать, сколько проехали на поезде? Как найдём?Что можем узнать дальше? Каким действием? Что можем узнать следующим действием?Каким действием? умноженияМожем ответить на вопрос задачи? Каким действием? Решаем самостоятельно. У доски решает учащийся.Проверяем. Поднимите руку, кто решил также? Задача решена правильно.Оцените решение задачи у доски?Физкультминуткаумение оформлятьсвои мысли в устнойформе.Регулятивные УУДконтроль в формесличения результатас заданным эталономс целью обнаруженияотклонений споследующейкоррекциейКакова длина всего маршрута?Нет. Потому, что не знаемсколько проехали на лодке?Нет, не знаем сколько проехали на поезде.Да.Действием сложенияСколько прошли пешком?Действием деления.Сколько проплыли на лодке.умноженияДаСложением.Учащийся комментирует решение задачи.1)40+240 к=280 (км)на поезде2)280:7=40(км)пешком3)40*3=120(км)на лодке4)40+280+40+120=480(км)Ответ: 480 километров длинавсего маршрута.

Выполняют физические
упражнения
IV. Первичноезакрепление спроговариванием вовнешней речи.Цель: учить применятьполученные знания оединицах измерениядлины при решениизадач. А теперь поработаем в группах.У вас на партах лежат карточки с заданием. Краткая запись к задаче сделана при помощи таблицыВыберите главного в группе. Вспомните правила работы в группе.Прочитайте задание.Заканчиваем работу. Проверяем работу групп.Сверьте правильность решения задачи с эталоном. ( Слайд6)Руководители групп – оцените каждого члена вашей группы на листочке с фамилиями, который лежит у вас на столе
Познавательные УУДконтроль и оценкарезультатовдеятельности:способность ксамооценке наоснове критерия успешности учебнойдеятельности. V. Самостоятельнаяработа ссамопроверкой поэталонуЗадание на карточках.Выполните самостоятельно задание на карточках. Решениезапишите в тетради. 1 вариант1.Сравните единицы длины. Поставьте знаки <,>,=10дм . 100см, 5м2дм . 52см 12см …1дм2см99см..9дм 8см2. Решите задачу:Автомобиль проехал в первый день120 км, а во второй на50 кмбольше. Сколько километров проехал автомобиль за два дня?2 вариант1. Сравните единицы длины. Поставьте знаки <,>,=6дм . 60см, 4м3дм . 3дм2см 24см …2дм4см81см…8дм 2см2. Решите задачу:Велосипедист проехал в первый день 30 км, а во второй в 2 разабольше. Сколько километров проехал велосипедист за два дня?Проверьте правильность решения по эталону. (Слайд7) Встаньте, кто справился с заданием без ошибок? VI. Включение всистему знаний иповторенийVII. РефлексияКакая тема урока у нас была? Достигли ли мы поставленных в начале урока целей?Через какие виды деятельности мы выполнили все задачи урока? Где могут пригодиться вам новые знания?1 вариант 1.Сравните единицы длины.Поставьте знаки<,>,=10дм=100 см 5м2дм>52см 12см=2см 99см>9дм8см 2.Решите задачу: 1)120км +50км=170(км)автомобиль проехал во второй день 2)120км+170км=290(км) Ответ: 290 километров проехалавтомобиль за 2 дня 2вариант6дм=60см4м3дм>3дм2см 24см=2дм4см81см<8дм2см2.Решите задачу: 1)30км х 2=60(км)велосипедист проехал во 2ой день2)30км+60км=90(км) Ответ: 90 километров проехалвелосипедист за 2 дня.
учебной деятельности Цель: осознаниеучащимися своейучебной деятельности,самооценка результатовсвоей и всего классадеятельностиVIII. ДомашнеезаданиеРебята, кому понравился урок? Предлагаю вам оценить своюработу.
У вас на партах лежат следы разных цветов. Зелёные всё понятноСиние –понятно, но возникли затрудненияКрасные ничего не понял, не запомнил (слайд8)Ответы детей. Оценивают свою работу.
Познавательные УУДконтроль и оценкарезультатовдеятельности:способность ксамооценке наоснове критерия успешности учебнойдеятельности. Запишите домашнее задание. (Слайд8)По выбору: С.

107 №5 или №6Спасибо за урок. Урок окончен. Желаю успехов!
Прямая ссылка на скачивание файла: Скачать файл
Урок математики 3 класс Учитель: Серкова Ирина ВалериевнаУМК: «Планета знаний», учебник «Математика» М.И. Башмаков,М.Г.НефёдоваТема урока: Вычисление длины пути.

Тип урока: изучения и первичного закрепления знанийПРЕЗЕНТАЦИЯМетоды: наглядный, словесный, диалог, частично-поисковый.
Формы организации деятельности учащихся: фронтальная, групповая, индивидуальная работа).
Урок построен с использованием информационно-коммуникативной технологии на основе технологии деятельностного подхода. Оборудование: учебник «Математика» 3 кл. Ч.
![]()
1 М. И. Башмаков,М.
Г. Нефёдова стр. 106-107, мультимедийная презентация, , карточки с заданиями для самостоятельной работы .
Цель урока: -учить вычислять длину пути;
![]()
-совершенствовать умения располагать единицы измерения пути в порядке возрастания. -повторение единиц измерения длины (сантиметр, метр, дециметр, километр).
None Образовательные: повторить единицы измерения пути, учить решать задачи на нахождение расстояния (пути), продолжать учить записывать краткую запись задач; сравнивать единицы измерения.
– совершенствовать вычислительные навыки (устные приемы вычислений в пределах 1000); – расширять математический кругозор учащихся.
![]()
Развивающие: Метапредметные:
формирование универсальных учебных действий (УУД). Личностные:
развивать учебно-познавательный интерес к учебному материалу и способам решения задач; формирование ценностно-смысловой ориентации учащихся в содержании учебного материала, в социальных ролях и межличностных отношениях, формирование личностных универсальных учебных действий.
![]()
Регулятивные: принимать и сохранять учебную задачу;
планировать свои действия в соответствии с поставленной задачей; оценивать правильность выполнения действия;
адекватно воспринимать предложения сверстников и учителя. Познавательные:
развивать познавательную активность,умение наблюдать, анализировать, делать выводы,умение устанавливать связи между единицами измерения(см, м, км),развивать внимание, наблюдательностьосуществлять работу с графической информацией (бланк с заданием в табличной форме);
обнаруживать пробелы в информации; владеть рядом общих приёмов решения задач.
Коммуникативные: строить монологическое высказывание, владеть диалогической формой коммуникации;
формировать умения учебного сотрудничества через работу в паре, в группеТехнологическая карта урока
|
Этап урока (цель этапа) |
Деятельность учителя. |
Деятельность учащихся. |
УУД. |
|
Ι. Мотивация к учебной деятельности Цель: включение учащихся в деятельность на личностном уровне. |
-Начинаем наш урок математики. а)Создание положительного эмоционального настроя:слайд1Математику, друзья. Нам не знать никак нельзя! Считать мы будем, рассуждать,Стараться знать ее на 5! б)Мотивация- Сегодня мы совершим очередное путешествие в мир математики. В какую область отправимся? (Какой раздел изучаем?)-Откройте тетради, запишите число 14 декабря. |
– Числа и величины. |
Коммуникативные УУД-уметь совместно договариваться о правилах поведения и общения на уроках и следовать им. |
|
ΙΙ. Актуализация знаний и фиксация затруднения в пробном учеб-ном действии. Цель: повторение материала, необходимого для «открытия нового знания», и выявление затруднений в инд.деятельност. |
Слайд 2. Для работы на уроке нам нужно повторить единицы измерения: Сравните: >,<, или =2ч. ? 110мин. None Вывод: Какие единицы измерения? |
None 95мин. = 1ч. 35мин. 100 дней 1 год24ч. 2 сут.
Самооценка по ЭТАЛОНУ (учитель) на доске+времениСтавят 1балл в тетради на поля |
Познавательные УУД-обобщение-анализ, синтез, выбор оснований для сравнений |
|
ΙΙΙ. Выявление места и причины затруднения. Цель: обсуждение затруднений, проговаривание цели урока в виде вопроса, на который предстоит ответить. |
Слайд 3– Какой путь Ёжика по- вашему короче? -Как найти длину пути Ёжика? Можем найти? Почему не можем узнать длину пути?! -Какие единицы измерения длины вы знаете? -А в каких единицах на данном рисунке можно измерить длину пути? -Расположите в порядке убывания эти единицы-Мы утром идём в школу. В каких единицах мы можем измерить расстояние от дома до школы? None -Мы подпишем единицы длины пути, можем найти расстояние, которое пройдёт Ёжик? |
Да,надо сложить все известные числа. Не знаем. Т. к. не указаны единицы измерения пути. Не знаем в чём измерять! None Аслан у доски, ост. в тетрадиСтавят 1балл в тетради на поля за прав.ответВ более крупных единицах- в километрах.
ПРОСМОТР мульт. «Профессор Почемушкин»Очень медленно передвигаетсяВ см или дмДа (8 м) |
None Регулятивные УУД-уметь высказывать своё предположение. None -умение оформлять свои мысли в устной форме. |
|
ΙV. Построение проекта выхода из затрудненияЦель: обсуждение затруднений, проговаривание цели урока (вопроса), на который предстоит ответить. |
-Предположите, какая тема нашего урока? -Сформулируйте цель урока. (Слайд 4)-Какие задачи поставим перед собой? (Слайд5)Тема: Длина пути |
Сегодня на уроке, я буду учиться вычислять длину пути. -повторить единицы измерения длины, сравнивать их-научиться вычислять длину пути |
None Регулятивные УУД-проявлять познавательную инициативу в сотрудн. |
|
V. Реализация построенного проекта. Цель: учить применять полученные знания при решении текстовых задач. |
Слайд 6 -Откройте учебник на с.106, задача.2. – Прочитайте задачу. -О чём говорится в задаче? – На каких видах транспорта? Запишем кратко или сделаем чертёж (на слайде и доске) и в тетрадях-Какие главные слова?- На чём? -Что значит втрое? – Какой вопрос задачи? – Можем ответить сразу? – Можем узнать сколько проехали на поезде?
-Как найдём? -Что можем узнать дальше? -Каким действием? -Что можем узнать следующим действием?. None -Каким действием?
Решаем самостоятельно. У доски решает учащийся. Проверяем. Взаимопроверка в парахПоднимите руку,кто решил также? Задача решена правильно. Оцените решение задачи в тетради товарища. Физкультминутка (слайд 7). |
None На автобусе-40км. На поезде-? км. на 240 км б. Пешком- ? км. В 7 раз м.
На лодке-? км. в 3 раза б. Какова длина всего маршрута? =Да. =Действием сложения=Сколько прошли пешком=Действием деления. =Сколько проплыли на лодке. =умножения=Сложением. Учащийся комментирует решение задачи. 1) 40+240 =280 (км)-на поезде2) 280:7=40 (км)–пешком3) 40*3=120 (км)-на лодке4) 40+280+40+120=480(км)Ответ: 480 километров длина всего маршрута. Ставят 2 балл в тетради на поляВыполняют физические упражнения для глаз и тела) |
None Регулятивные УУД- саморегуляцияКоммуникативные УУД-умение оформлять свои мысли в устной форме.
Регулятивные УУД-контроль в форме сличения результата с заданным эталоном с целью обнаружения отклонений с последующей коррекцией |
|
VΙ. Первичное закрепление с проговариванием во внешней речиЦель: учить применять полученные знания о единицах измерения длины при решении задач. |
-А теперь (Слайд 8)поработаем в группах. У вас на партах лежат карточки с заданием . Такие задания бывют в Всеросс.проверочных работах (ВПР)Краткая запись к задаче сделана при помощи таблицы1) Выберите главного в группе. 2) Вспомните правила работы в группе. 3) Выполняйте задание. Сравните результаты соревнований. В этом соревновании учитывается только лучшая попытка спортсмена. Запишите её в графу- с ?
? Заканчиваем работу. Проверяем работу групп. 4) Сверьте правильность решения задачи с эталоном.(Слайд 9)5) Руководители групп – оцените каждого члена вашей группы на листочке с именем в 1 балл ,который лежит у вас на столе |
Организуются для работы в 2 группах. Читают задание.
Кто показал лучший результат? Записывают имена всех участников в порядке уменьшения результатов. Первая группа –Сравнив результаты, мы пришли к выводу, что лучший результат у Вити и Гоши. Вторая группа – второй результат у Бори. Третья группа-Третий результат у Антона. Руководители групп оценивают участие каждого члена группы и выставляют оценки (Ставят 1 балл за работу) на лист |
|
|
None Слайд 10)9.Рефлексия учебной деятельностиЦель: осознание учащимися своей учебной деятельности, самооценка результатов своей и всего класса деятельности10. ОЦЕНИВАНИЕ |
Выполните самостоятельно задание на карточках. Выразите единицы длины. Продолжить10 дм = …см,5 м = ….см42 см = …дм….см99 мм = …см …мм7 км = ………мПроверьте правильность решения по эталону-Какая была тема урока?
Достигли ли мы поставленных в начале урока целей? -Чему вы учились? Где могут пригодиться вам новые знания? Запишите По выбору: С. 106 №3 или №5Предлагаю вам оценить свою работу. У нас на Слайде 11 следы разных цветов.
Зелёные – значит всё понятно! Синие – понятно, но возникли затрудненияКрасные – ничего не понял, не запомнил- Посчитайте баллы в ваших тетрадях (5 б- «5», 4 б – «4» и тд.)Спасибо за урок. Урок окончен |
None Оценивают свою работу- встают на месте. |
None Познавательные УУД-контроль и оценка результатов деятель-ности: способность к самооценке на основе критерия успешности учебной деятель-ности. |
None Вычисление длины путиТип урока:
None Формы организации деятельности учащихся: фронтальная, групповая,индивидуальная Урок построен с использованием информационнокоммуникативной технологии на основе технологии деятельностного подхода.
Оборудование:
учебник Математика» 3 кл. Ч.1 М.И. Башмаков,М.Г.Нефёдова стр.106-107, мультимедийная презентация, , карточки с заданиями для самостоятельной работы . учить вычислять длину пути; совершенствовать умения располагать единицы измерения пути впорядке возрастания.
повторение единиц измерения длинысантиметрметр, дециметр, километрформирование умений решать текстовые задачи, содержащие единицы измерения длиныповторить единицы измерения пути, учить решать задачи на нахождение расстояния (пути), продолжать учить записывать краткую запись задач; сравнивать единицы измерения.
None расширять математический кругозор учащихся.
None развивать учебнопознавательный интерес к учебному материалу и способам решения задач;
None принимать и сохранять учебную задачу;
планировать свои действия в соответствии с поставленной задачей; оценивать правильность выполнения действия;
адекватно воспринимать предложения сверстников и учителя.
развивать познавательную активность, умение наблюдать, анализировать, делать выводы, умение устанавливать связи между единицами измерения(см, м, км), развивать внимание, наблюдательность осуществлять работу с графической информацией (бланк с заданием в табличной форме);
обнаруживать пробелы в информации; владеть рядом общих приёмов решения задач.
None формировать умения учебного сотрудничества через работу в паре, в группе
None а)Создание положительного эмоционального настроя:
слайд1Нам не знать никак нельзя!
Считать мы будем, рассуждать,Сегодня мы совершим очередное путешествие в мир математики. В какую область отправимся? Откройте тетради, запишите Для работы на уроке нам нужно повторить единицы измеренияКакой путь Ёжика повашему Как найти длину пути ЁжикаПочему не можем узнать длину Какие единицы измерения длины А в каких единицах на данном рисунке можно измерить длину Расположите в порядке убывания Мы утром идём в школу. В каких единицах мы можем измерить расстояние от дома до школы? Не знаем. Т. к. не указаны
А расстояние от нашего села до Уфы? (57 км) до Москвы(1371 А расстояние от Земли до Луны? А путь, который проползёт черепашка за 1 минуту в чём Мы подпишем единицы длины пути, можем найти расстояние, В более крупных единицахПредположите, какая тема Сформулируйте цель урока.
None На каких видах транспорта?
None На чёмМожем узнать сколько проехали Что можем узнать дальше? Что можем узнать следующим Каким действием?
None На лодке? км. в 3 раза б.
Поднимите руку,кто решил также?
Оцените решение задачи в тетради Физкультминутка(слайд 7)3) 40*3=120 (км)на лодкеУ вас на партах лежат карточки с заданиемТакие задания бывют в Всеросс.проверочных работах Краткая запись к задаче сделана 1) Выберите главного в группе. 2) Вспомните правила работы в соревновании учитывается только лучшая попытка спортсмена. Запишите её в графус ??
4) Сверьте правильность решения задачи с эталоном.(Слайд 95) Руководители групп –оцените каждого члена вашей группы на листочке с именем в 1 балл,который лежит у вас на столеОрганизуются для работы в оценивают участие каждого членагруппыи выставляют Проверьте правильность решения

Достигли ли мы поставленных в Где могут пригодиться вам Запишите По выбору: С. 106 №3 Предлагаю вам оценитьсвою У нас на Слайде 11следы разных Зелёныезначит всё понятноСиние –понятно, но возникли Красныеничего не понял, не Посчитайте баллыв ваших тетрадях(5 б5», 4 б –«4» и тд.)Спасибо за урок. Урок окончен
Линия, которую описывает материальная точка при своем движении, называется траекторией.
ОпределениеДлиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени от t1 до t2. В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
В цилиндрических координатах длина пути может быть выражена как:
В сферических координатах формулу длины пути запишем:

Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени материальная точка проходит путь ds, который называют элементарным. При этом:
где – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна: где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути на отрезке времени от до находят как:
где – средняя путевая скорость. При равномерном движении .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как: где a – постоянное ускорение, v0 – начальная скорость движения.
[custom_ads_shortcode1]
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=мВ СГС: [s]=см
[custom_ads_shortcode2]
Примеры решения задач
ПримерЗадание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4. Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
![]()
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
Ответ. Путь равен 20 м, перемещение равно 4 м.
None Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения задачи примем формулу пути в виде:
Подставим в (2.1) функцию x=-0,2t2, учтем, что имеем:
Ответ. s=5м.
None Вы поняли, как решать? Нет?
![]()
Источники:
- znanio.ru
- xn--j1ahfl.xn--p1ai
- uchitelya.com
- www.webmath.ru





