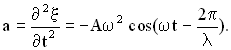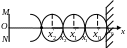Как найти длину упругой волны

1.1. Упругие продольные и поперечные волны

1.2. Характеристики бегущих волн

1.2.1. Длина волны

1.2.2. Фазовая скорость волны

1.2.3. Фазовая скорость различна для разных сред

1.2.4. Фронт волны. Волновая поверхность

1.2.5. Уравнение бегущей волны

1.2.6. Волновое уравнение

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

1.3. Энергия упругих волн

1.4. Принцип суперпозиции волн. Групповая скорость

1.5. Интерференция волн. Стоячие волны

1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.

Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.

Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.

2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.

Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.

Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.

1.1. Упругие продольные и поперечные волны

Все волны делятся на продольные и поперечные.

Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.

Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.

Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.

1.2. Характеристики бегущих волн

1.2.1. Длина волны

Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.

Длиной волны называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна ).

Если точки разделены расстоянием , их колебания происходят в противофазе.

1.2.2. Фазовая скорость волны

Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.

Фазовая скорость – это скорость распространения данной фазы колебаний, т.е. скорость волны.

Связь длины волны , фазовой скорости и периода колебаний Т задается соотношением:

.

Учитывая, что , где – линейная частота волны, – период, а циклическая частота волны , получим разные формулы для фазовой скорости:

.

Для волнового процесса характерна периодичность по времени и по пространству.

Т – период колебаний точек среды. Роль пространственного периода играет длина волны . Соотношение между периодом и циклической частотой задается формулой: . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: .

Таким образом. Можно добавить еще одно уравнение для фазовой скорости:

.

1.2.3. Фазовая скорость различна для разных сред

В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:

,

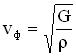
где – модуль сдвига среды, -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Фазовая скорость упругих продольных волн в твердом теле равна

,

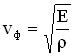
где Е – модуль Юнга, – плотность невозмущенной среды (твердого тела до момента распространения по нему волны).

Фазовая скорость продольных волн в жидкости и газе определяется соотношением: ,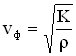

где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, – плотность невозмущенной среды.

Фазовая скорость продольных волн в идеальном газе задается формулой: ,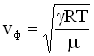

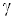
– показатель адиабаты, – молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа () и от его термодинамического состояния (Т).

1.2.4. Фронт волны. Волновая поверхность

При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.

Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.

Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.

Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.

При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.

Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.

Если известно положение фронта волны в некоторый момент времени и скорость волны , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.

1.2.5. Уравнение бегущей волны

Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.

Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.

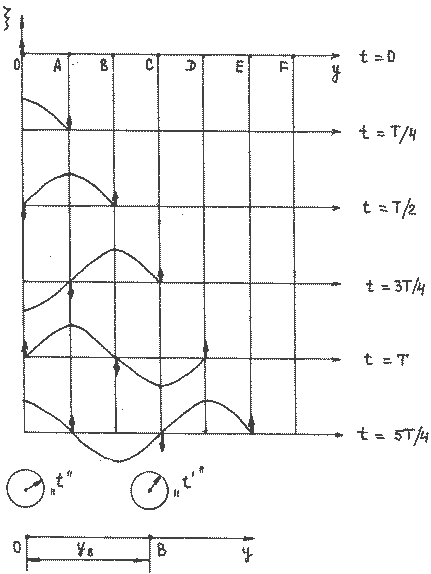
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О – центр (источник) колебаний, она колеблется по закону:

,

где – смещение точки О от положения равновесия, – частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.

Через промежуток времени процесс колебаний дойдет до точки В, и она будет колебаться по закону: .

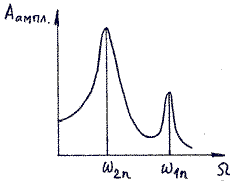
Рисунок 2.1.1.

Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время . Моменты времени t и связаны между собой соотношением или . Расстояние между точками О и В обозначим . Фазовая скорость волны равна , тогда . 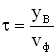Учитывая соотношения для и и формулы и , можно записать уравнение колебаний точки В в разных видах:

.

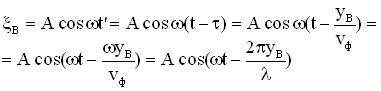
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:

,

где – волновое число (см. определение выше).

Это уравнение и есть уравнение для смещения любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина – фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.

Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.

Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:

.

Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.

1.2.6. Волновое уравнение

Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:

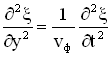
, где – фазовая скорость волны.

Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что есть функция двух переменных t и y.

1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды

Если смещение любой точки среды с координатой y в момент времени t задано уравнением:

,

то скорость этой точки есть величина , а ускорение – :

,

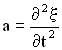
1.3. Энергия упругих волн

В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме равна: , где – объемная плотность среды.

Если выбранный объем записать как , где S – площадь его поперечного сечения, а – его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком через его поверхность:

.

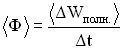
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.

Эта величина определяется соотношением:

,

где 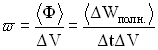-объемная плотность энергии волны, – фазовая скорость волны. Так как фазовая скорость волны – вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:

.

Величина , вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова – Пойнтинга.

Интенсивностью волны называется модуль среднего значения вектора Умова .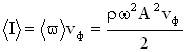

1.4. Принцип суперпозиции волн. Групповая скорость

Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.

Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.

На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.

В общем виде связь между групповой и фазовой скоростями имеет вид:

.

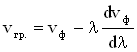
1.5. Интерференция волн. Стоячие волны

1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.

В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна , т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.

Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.

2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники и испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника , а от второго – .

Колебания точки М под действием волн от двух источников и описываются уравнениями:

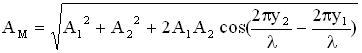
, . Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”): . Амплитуда колебаний точки М максимальна (), если , где Величина называется разностью хода двух волн. Условие максимума при интерференции имеет вид: . Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (), если , (). Условие минимума при интерференции имеет вид: . Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид: , Суммарное смещение частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений и : .

Это и есть уравнение стоячей волны. Величина 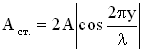– амплитуда, а () – фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.

В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:

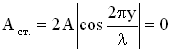
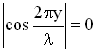
, отсюда следует . Выполнение этого соотношения будет при условии для Итак, координаты узлов задаются формулой:

.

Расстояние между двумя соседними узлами равно .

Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:

.

Это уравнение можно получить из условия максимума амплитуды

, т.е. . Последнее соотношение выполняется при значениях аргумента ().

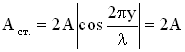
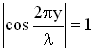
Расстояние между двумя соседними пучностями равно .

4. Изменение фазы волны при ее отражении.

Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на радиан соответствует появлению дополнительного хода луча, равного .

4.1. Примеры решения задач

Пример 1

Звуковые колебания,
имеющие частоту ν = 500 Гц и амплитуду A
= 0,25 мм, распространяются в воздухе.
Длина волны λ
= 70 см. Найти скорость υ
распространения колебаний и максимальную
скорость

частиц воздуха.

Дано: ν = 500 Гц A = 0,25 мм = 2,5·10-4 м λ = 70 см = 0,7 м	Решение: 1). Скорость распространения колебаний (фазовая скорость) связана с длиной λ волны и частотой колебаний ν соотношением υ= Следовательно, фазовая скорость υ = 0,7·500 = 350 м/с.
υ – ? – ?

2). Уравнение плоской
волны имеет вид

,

где ξ =
ξ(l,
t)
– смещение точки, находящейся на
расстоянии x
от источника колебаний, в момент времени
t;

A
– амплитуда колеблющихся точек;

k
=


– волновое число.

Скорость точек
среды, в которой распространяется волна,
можно найти, продифференцировав волновое
уравнение по времени:

.

Если

=1,
то скорость частиц в воздухе будет
максимальной и равной

= 2,5·10^-4·2·π·500
= 0,785 м/с.

Ответ:
υ
= 350 м/с;

= 0,785 м/с.

Пример 2*

Смещение от
положения равновесия точки, отстоящей
от источника колебаний на расстояние
l₁
= 4 см, в момент времени t₁
=


равно половине амплитуды. Найти длину
λ бегущей волны.

Дано: l1 = 4 см t1 =	Решение: По условию, смещение точки, находящейся на расстоянии l1 от источника колебаний, в момент времени t1 равно С другой стороны, это же смещение можно выразить из уравнения бегущей волны
λ – ?

Приравнивая правые
части обоих равенств, получаем, что

,

Следовательно
, (1)

где

– циклическая частота колебаний;

– волновое число.

Тогда с учетом
того, что t₁
=

,
выражение (1) приобретает следующий вид:

Отсюда находим,
что

и, следовательно, длина волны

λ
= 12l₁
= 12·4 = 48 см.

Ответ:
λ =
48 см.

Пример 3*

Найти разность
фаз

колебаний двух точек, отстоящих от
источника колебаний на расстоянии

м
и

м.
Период колебаний

с;
скорость распространения

м/с.

Дано: м м с м/с

-?

Решение:

Смещение точки

,
отстоящей от источника колебаний на
расстояние

в момент времени

,
определяется из уравнения волны

где (
)
– фаза колебаний данной точки в данный
момент времени.

Тогда фаза первой
точки в момент времени

:

,
а фаза второй точки в этот же момент
времени

.

Следовательно,
разность фаз этих двух точек

равна

.

.

рад,
т.е. точки, колеблются в противофазе.

Ответ:

рад.

Пример 4

Один конец упругого
стержня соединен с источником гармонических
колебаний, подчиняющихся закону

,
а другой его конец жестко закреплен.
Учитывая, что отражение в месте закрепления
стержня происходит от менее плотной
среды, определите характер колебаний
в любой точке стержня.

Дано: Среда менее плотная

Решение:

,

,

,

,
,

.

При

– пучности стоячей волны (
).

При

– узлы стоячей волны (
).

Пример 5.

На расстоянии l=4м
от источника плоской волны частотой

Гц
перпендикулярно ее лучу расположена
стена. Определить расстояния от источника
волн до точек, в которых будут первые
три узла и три пучности стоячей волны,
возникшей в результате сложения бегущей
и отраженной от стены волн. Скорость
волны считать равной 440 м/c.

Дано: l=4м Гц м/с

Р

ешение:

Ось

направим вдоль луча бегущей волны, а
начало О
координат совместим с точкой, находящейся
на источнике MN
плоской волны (см. рис).

С учетом этого
уравнение бегущей волны запишется в
виде

. (1)

Поскольку в точку
с координатой x
волна возвратится, пройдя дважды
расстояние

,
и при отражении от стены, как среды более
плотной, изменит фазу на

,
то уравнение отраженной волны можно
записать в виде

.

После тригонометрических
преобразований получим

. (2)

Уравнение стоячей
волны найдем, складывая уравнения (1) и
(2):

.

Воспользовавшись
формулой разности косинусов, получим

.

Так как выражение

не зависит от времени, то, взятое по
модулю, оно может рассматриваться как
амплитуда стоячей волны:

. (3)

Зная выражение
амплитуды (3) стоячей волны можно найти
координаты узлов и пучностей.

Узлы возникают в
тех точках, где

.
Это равенство выполняется для точек,
координаты

которых удовлетворяют условию

. (4)

Учитывая, что

(5)

выражение (4)
перепишется в виде:

,

Откуда находим
координаты узлов:

, n
= 0,1,2,3…

Подставив сюда
значения

и

найдем координаты первых трех узлов:

;

;

.

Пучности возникают
в тех точках, где амплитуда (3) стоячей
волны максимальна:

Отсюда следует,
что

(6)

С учетом (5) выражение
(6) перепишется в виде

откуда находим
координаты пучностей

, n
= 0,1,2,3,…

Подставив сюда
значения

и

получаем координаты первых трех
пучностей:

;

;

.

Изобразим на
рисунке границы максимальных смещений
точек среды в зависимости от их координат.

– координаты узлов
стоячей волны;

– координаты
пучностей стоячей волны.

Ответ:
координаты узлов:

;

;

;

координаты
пучностей:

;

;

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Длина волны

О чем эта статья:

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

• Например, радиоволны, Wi-Fi и свет.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.

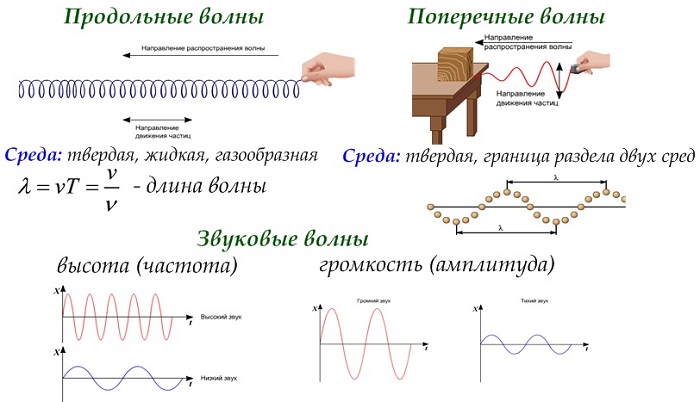
Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

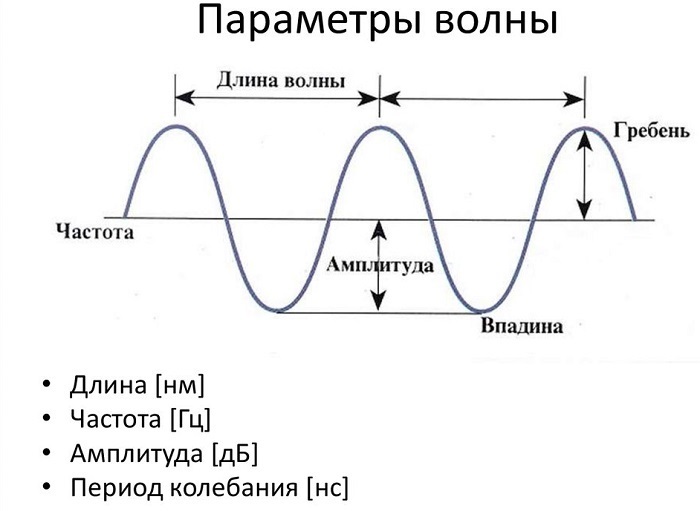
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны

T = t/N

N — количество колебаний [—]

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости

𝑣 = S/t

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Формула скорости волны

𝑣 = λ/T

λ — длина волны [м]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

Возьмем формулу скорости:

Нам известна длина волны, но не дан период. Период вычисляется по формуле:

Теперь подставляем величины в формулу

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

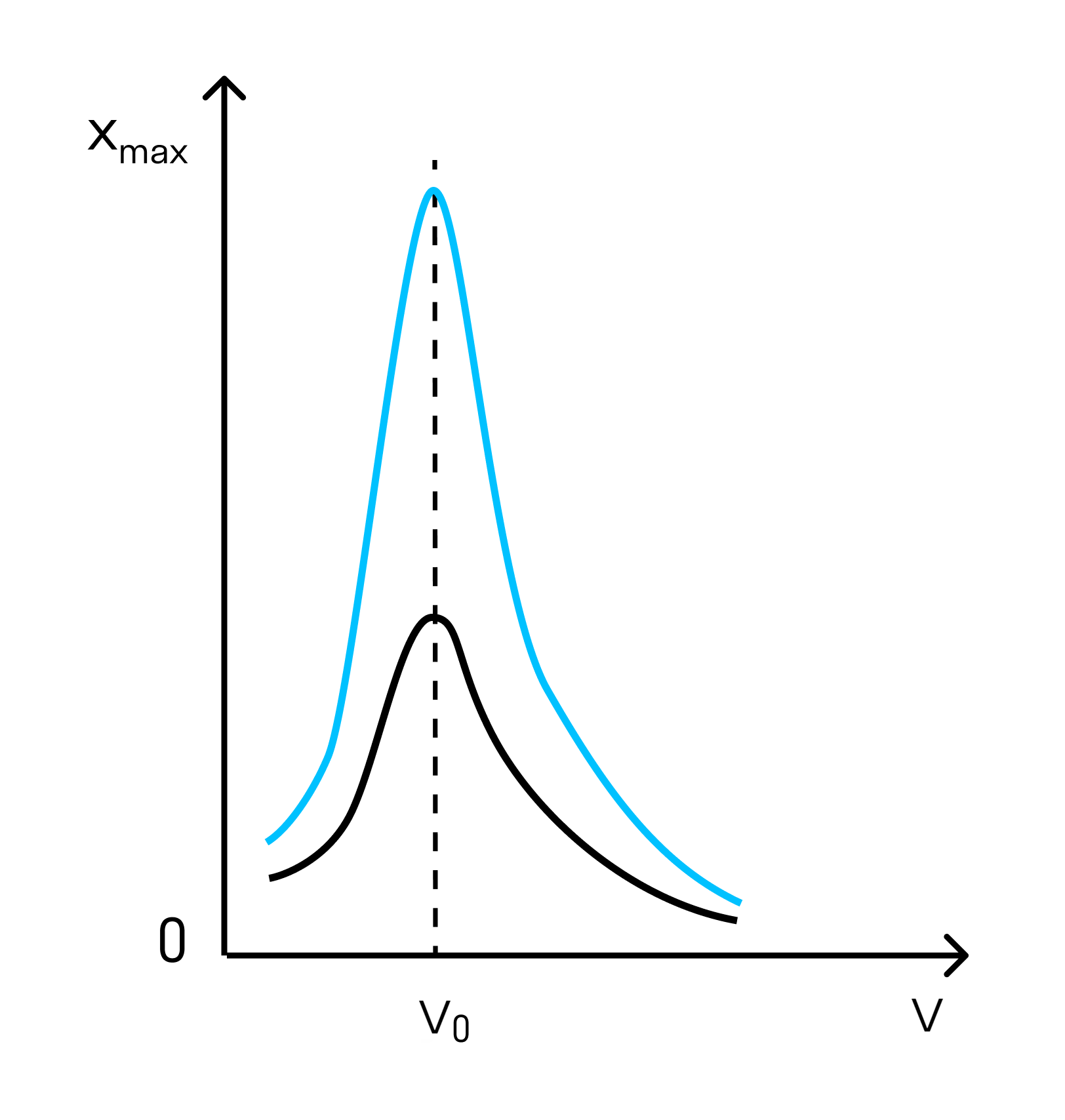
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты

ν = N/t

N — количество колебаний [—]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Длина волны – формулы, свойства и расчеты

Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

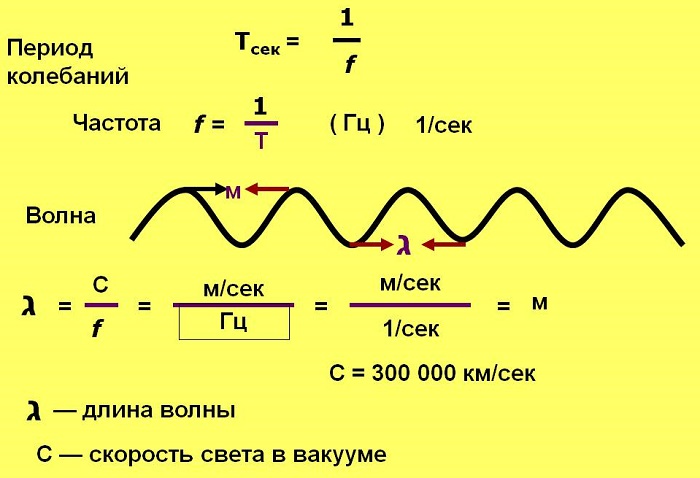
Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10 8 м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

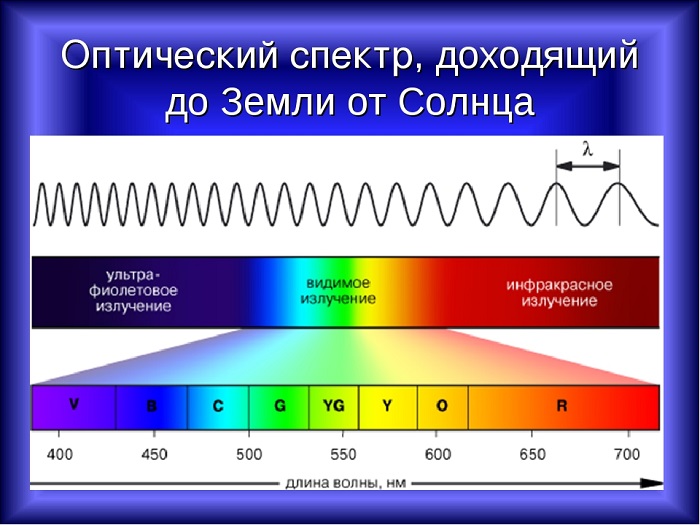
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

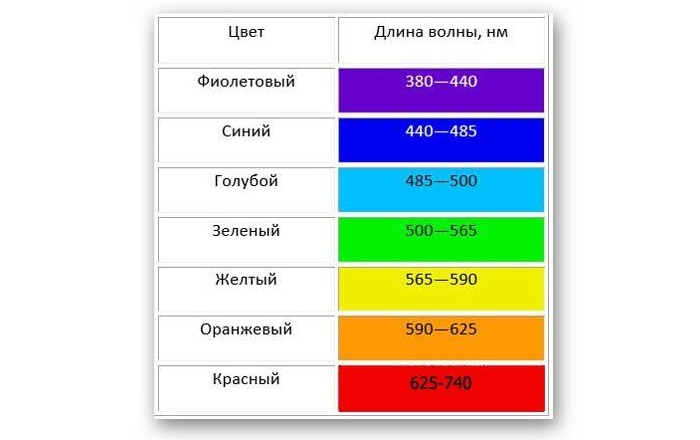
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

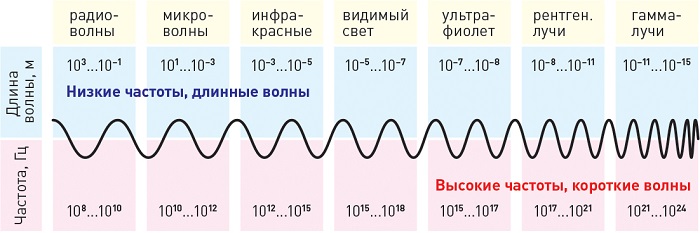
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Длина волны. Скорость распространения волны (Ерюткин Е.С.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

В ходе урока вы сможете самостоятельно изучить тему «Длина волны. Скорость распространения волны». На этом уроке вы сможете познакомиться с особенными характеристиками волн. В первую очередь вы узнаете, что такое длина волны. Мы рассмотрим ее определение, способ ее обозначения и измерения. Затем мы также подробно рассмотрим скорость распространения волны.

[spoiler title=”источники:”]

http://nauka.club/fizika/dlina-volny.html

http://interneturok.ru/lesson/physics/9-klass/mehanicheskie-kolebaniya-i-volny/dlina-volny-skorost-rasprostraneniya-volny-eryutkin-e-s

[/spoiler]

Механические волны.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механические волны, длина волны, звук.

Механические волны – это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).

Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.

Продольные и поперечные волны.

Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис. 1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е. перпендикулярно слоям).

Рис. 1. Продольная волна

Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.

Рис. 2. Поперечная волна

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.

Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.

Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.

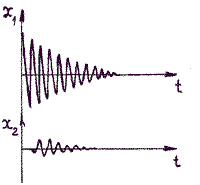
Рассмотрим процесс распространения волны более подробно. Допустим, что некоторая частица среды (частица ) начала совершать колебания с периодом . Действуя на соседнюю частицу она потянет её за собой. Частица в свою очередь, потянет за собой частицу и т. д. Так возникнет волна, в которой все частицы будут совершать колебания с периодом .

Однако частицы имеют массу, т. е. обладают инертностью. На изменение их скорости требуется некоторое время. Следовательно, частица в своём движении будет несколько отставать от частицы , частица будет отставать от частицы и т. д. Когда частица пустя время завершит первое колебание и начнёт второе, своё первое колебание начнёт частица , находящаяся от частицы на некотором расстоянии .

Итак, за время, равное периоду колебаний частиц, возмущение среды распространяется на расстояние . Это расстояние называется длиной волны. Колебания частицы будут идентичны колебаниям частицы колебания следующей частицы будут идентичны колебаниям частицы и т. д. Колебания как бы воспроизводят себя на расстоянии можно назвать пространственным периодом колебаний; наряду с временным периодом она является важнейшей характеристикой волнового процесса. В продольной волне длина волны равна расстоянию между соседними сжатиями или разрежениями (рис. 1). В поперечной – расстоянию между соседними горбами или впадинами (рис. 2). Вообще, длина волны равна расстоянию (вдоль направления распространения волны) между двумя ближайшими частицами среды, колеблющимися одинаково (т. е. с разностью фаз, равной ).

Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:

.

Частотой волны называется частота колебаний частиц:

.

Отсюда получаем связь скорости волны, длины волны и частоты:

. (1)

На поверхности жидкости могут существовать волны особого типа, похожие на поперечные – так называемые поверхностные волны. Они возникают под действием силы тяжести и силы поверхностного натяжения.

Звук.

Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше – область ультразвука.

К основным характеристикам звука относятся громкость и высота.
Громкость звука определяется амплитудой колебаний давления в звуковой волне и измеряется в специальных единицах –децибелах (дБ). Так, громкость 0 дБ является порогом слышимости, 10 дБ – тиканье часов, 50 дБ – обычный разговор, 80 дБ – крик, 130 дБ – верхняя граница слышимости (так называемый болевой порог).

Тон – это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.

Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах – больше, чем в жидкостях.
Например, скорость звука в воздухе при равна примерно 340 м/с (её удобно запомнить как “треть километра в секунду”)*. В воде звук распространяется со скоростью около 1500 м/с, а в стали – около 5000 м/с.
Заметим, что частота звука от данного источника во всех средах одна и та же: частицы среды совершают вынужденные колебания с частотой источника звука. Согласно формуле (1) заключаем тогда, что при переходе из одной среды в другую наряду со скоростью звука изменяется длина звуковой волны.

Если хочешь найти расстояние до грозовых туч в километрах, посчитай, через сколько секунд после молнии придёт гром, и раздели полученное число на три.

Как найти длину волны

Для расчета и проектирования радио- и телевизионных приемников и передатчиков, средств навигации, оптического и медицинского оборудования и во многих других отраслях науки и техники бывает необходимо рассчитать длину волны.

Вам понадобится

• частота волны, скорость распространения света в среде.

Инструкция

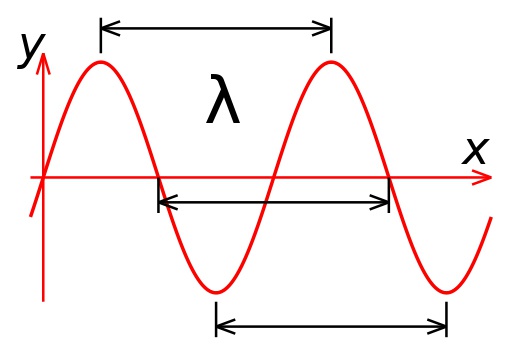
Хотя длина волны равна расстоянию между двумя любыми точками, которые колеблются синфазно, обычно за длину волны принимают расстояние между ее гребнями. Измеряется эта величина в единицах расстояния.Длина волны обратно пропорциональна ее частоте. Единица измерения частоты Гц. Например, частота промышленного тока в РФ – 50 Гц. Однако для передачи радио- и телевизионных сигналов используют более высокие частоты. Предположим, вам известно, что ваша любимая радиостанция работает на частоте 1,5 МГц, а шкала вашего радиоприемника градуирована в метрах. Вам нужно найти волну, на которой будете ее слушать. Сначала запомните, чему равны сокращенные обозначения величин:к – кило, 103=1000
М – мега, 106=1 000 000Переведите МГц в Гц:
1,5 МГц=1500000 Гц

Длину волны можно найти, разделив скорость света в вакууме на частоту волны. Скорость света в воздухе практически равна скорости света в вакууме. Рентгеновское излучение, радиоволны и электромагнитные волны распространяются со скоростью света. Следовательно, длина радиоволны частотой 1,5 МГц равна:
300000000/1500000=200 м
Итак, ищите любимую радиостанцию в диапазоне 200 м.

Чем выше частота волны, тем меньше ее длина. Различают длинные волны (ДВ), лежащие в диапазоне от 1000 м до 10000 м, средние волны (СВ) – от 100 м до 1000м, короткие (КВ) – от 10 м до 100 м, и ультракороткие (УКВ) – от 10-6м до 10 м.
Длинные волны распространяются на расстояние до 2000 км за счет отражения от поверхности земли и границы раздела верхних слоев атмосферы.
Средние волны гасятся поверхностью земли, отражаясь ночью от ионосферы. Дальность их распространения зависит от времени суток, т.к. в дневное время активный слой ионосферы поглощает радиоволны.
Короткие волны распространяются на большие расстояния, отражаясь поочередно от поверхности земли и от ионосферы.При распространении волны в различных средах ее длина может изменяться при одной и той же частоте, в зависимости от свойств среды.

Видео по теме

Обратите внимание

При распространении волны в анизотропной среде нужно учитывать фазовую и групповую скорости.

Полезный совет

Имейте в виду, что длина упругой волны рассчитывается по этой же формуле.

Источники:

• сайт, посвященныйтелекоммуникационным технологиям

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?