Как найти длину в физике колебания

Расчет длины маятника

Маятник — это тело или система тел, подвешенная в поле тяжести и совершающая механические колебания.

Формула расчета длины маятника:

L = (T / 2π) 2 * g, где

L — длина маятника в метрах;
T — период колебаний в секундах;
g — ускорение свободного падения в м/с 2 .

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета длины маятника по простой математической формуле в зависимости от периода колебаний и ускорения свободного падения. С помощью этой программы вы в один клик сможете рассчитать длину маятника.

Расчет длины нити математического маятника

Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле , где — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет секунды.

Решение задачи

В данном уроке показано, как грамотно рассчитать длину нити математического маятника. По условию задана формула , с помощью которой приблизительно вычисляются колебания маятника. — это период колебания маятника, который известен по условию задачи ( секунды), а – это длина нити маятника, которую и необходимо рассчитать. Для решения задачи достаточно преобразовать формулу (представленную в виде алгебраического выражение) и подставить в нее известные данные. Для этого из формулы выражается переменная , в процессе этого выполняются операции упрощения выражения. Далее, для получения окончательного ответа, вместо переменной подставляется его числовое значение. Ответ представлен в виде десятичной дроби

При подготовке к ОГЭ можно успешно воспользоваться решением этой задачи, в частности при решении задач типа ОГЭ 20.

Как найти длину нити

Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол появляется касательная составляющая силы тяжести (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Если обозначить через линейное смещение маятника от положения равновесия по дуге окружности радиуса , то его угловое смещение будет равно . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению , а

Только в случае малых колебаний , когда приближенно можно заменить на математический маятник является гармоническим осциллятором , т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка ; при этом величина отличается от не более чем на . Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение маятника пропорционально его смещению , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника .

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс физического маятника находится ниже оси вращения на вертикали, проходящей через ось. При отклонении маятника на угол возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь – расстояние между осью вращения и центром масс .

Здесь – собственная частота малых колебаний физического маятника .

Более строгий вывод формул для и можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение есть вторая производная углового смещения по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции можно выразить через момент инерции относительно оси, проходящей через центр масс маятника и параллельной оси вращения:

Окончательно для круговой частоты свободных колебаний физического маятника получается выражение:

автор вопроса выбрал этот ответ лучшим

Длина волны

О чем эта статья:

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

• Например, радиоволны, Wi-Fi и свет.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.

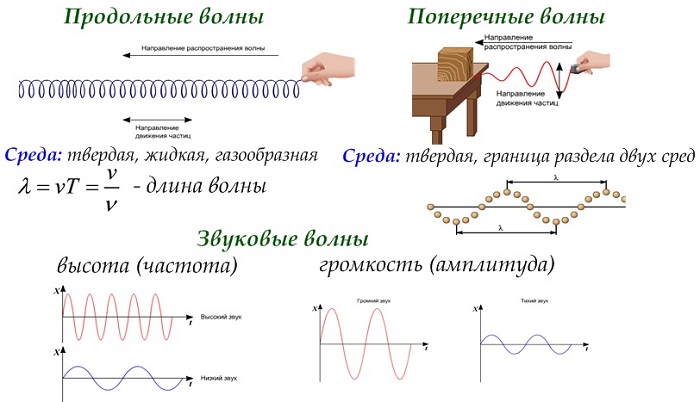
Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны

T = t/N

N — количество колебаний [—]

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости

𝑣 = S/t

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Формула скорости волны

𝑣 = λ/T

λ — длина волны [м]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

Возьмем формулу скорости:

Нам известна длина волны, но не дан период. Период вычисляется по формуле:

Теперь подставляем величины в формулу

Резонанс

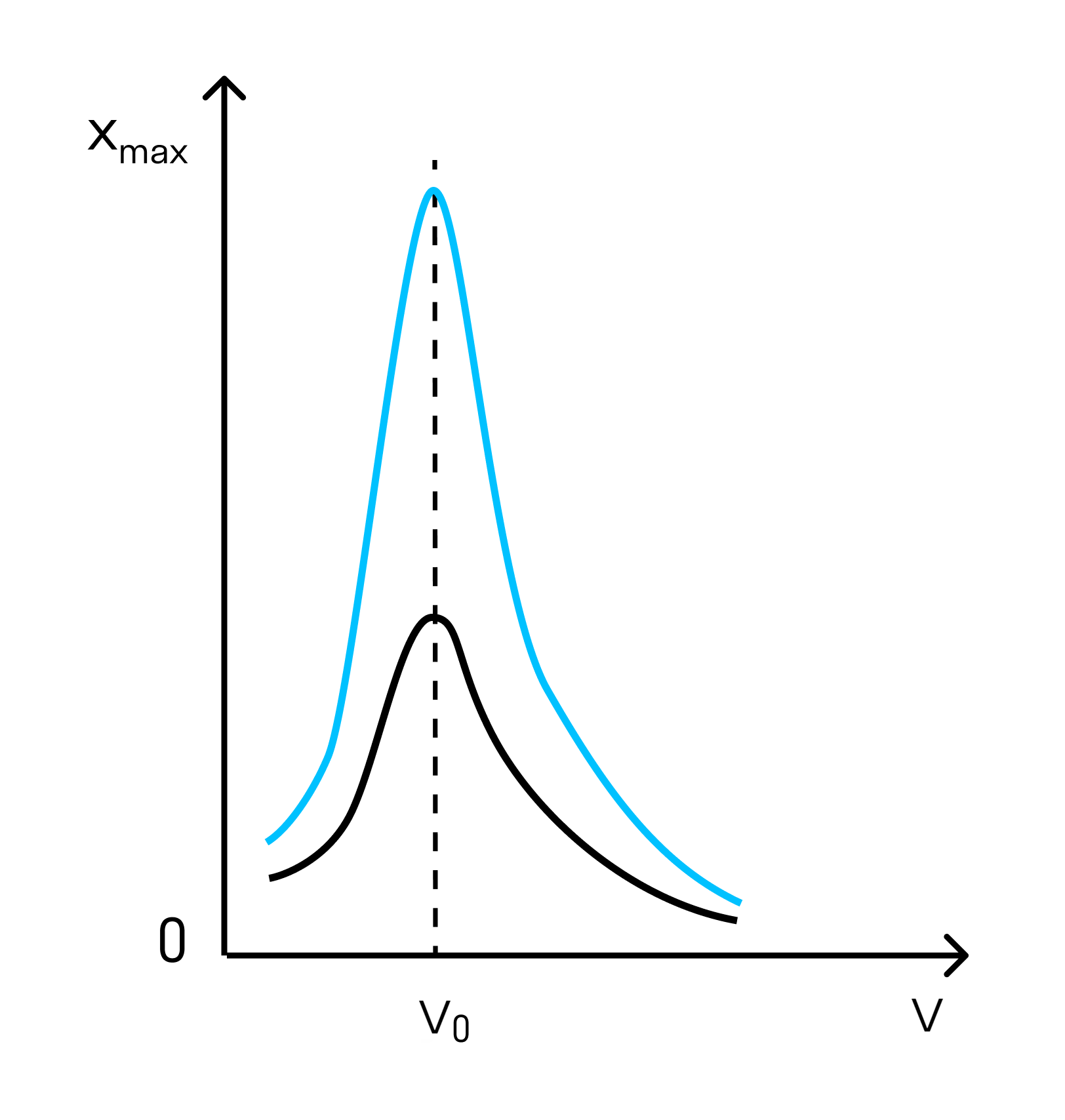
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты

ν = N/t

N — количество колебаний [—]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Длина и скорость волны.

Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают ско­рость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.

Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

,

где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.

Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что пери­од колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:

,

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.

Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотогра­фии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направле­нием распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.

Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания час­тиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.

Длина волны – формулы, свойства и расчеты

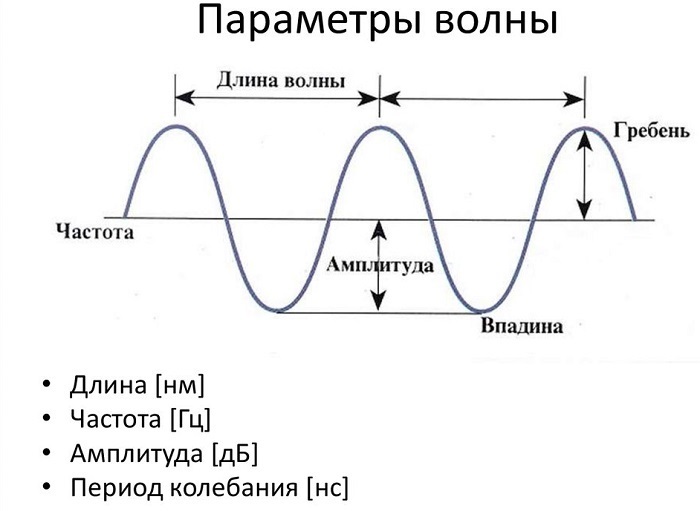
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

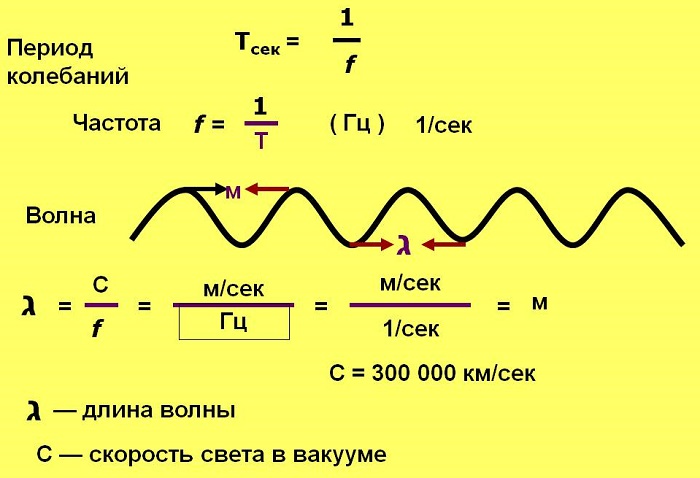
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10 8 м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

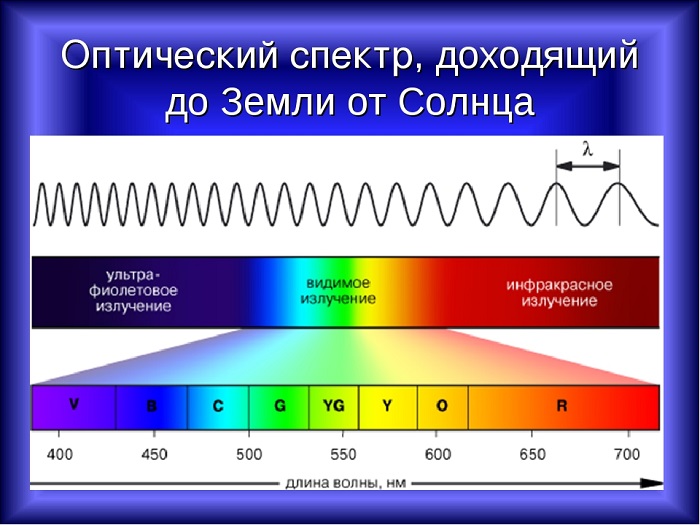
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

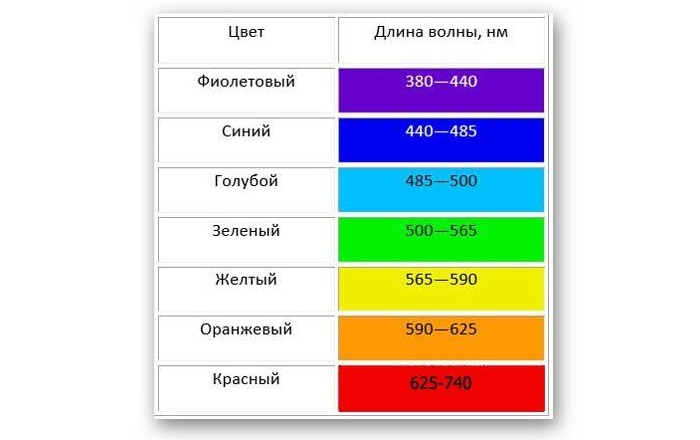
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

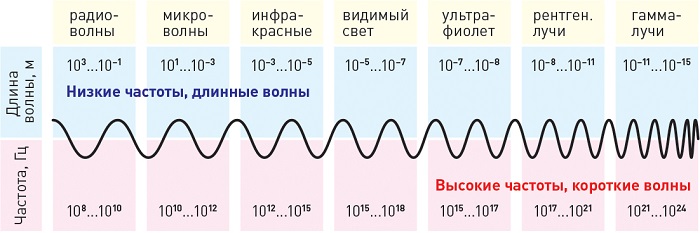
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

[spoiler title=”источники:”]

http://www.calc.ru/Dlina-I-Skorost-Volny.html

http://nauka.club/fizika/dlina-volny.html

[/spoiler]

1. Математический
маятник – модель состоит из материальной
точки подвешенной не длине невесомой
и нерастяжимой нити совершающей колебания
в вертикальной плоскости под действием
силы тяжести.

При
движении материальной точки совершается
вращательное

движение относительно
оси проходящей через точку подвеса О.

Так как линия
действующего натяжения нити проходит
через ось

вращения то ее
момент относительно оси равен 0.

На Ох:
.
При малых углах отклонения от
вертикали,можно считать чтоsinα≈α.

Решением этого
уравнения является функция вида:
–
математический маятник совершает
колебания по гармоническому закону.-период
колебания математического маятника не
зависит от массы маятника, а зависит от
его длины и ускорения свободного падения
в том месте где подвешен маятник.

2. Физическим
маятником называется твердое тело,
закрепленное на неподвижной горизонтальной
ocи (оси подвеса), не проходящей через
центр тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести. В отличие от математического
маятника массу такого тела нельзя
считать точечной.
Считая
колебания малыми положим чтоsinφ=φ,
тогда
–
дифференциальное уравнение гармонических
колебаний решением которого является.Период
физического маятника.Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического маятника,
т.е.  или

Из этого соотношения
определяем
.
Данная формула определяет приведенную
длину физического маятника, т.е. длину
такого математического маятника, период
колебаний которого равен периоду
колебаний данного физического маятника.

Вопрос 43. Затухающие
колебания. Дифференциальное уравнение
затух колеб и его решение. Логарифмический
дискремент и коэффициет затухания.
Затухающие
колебания – это колебания, амплитуда
которых из-за потерь энергии реальной
колебательной системы с течением времени
уменьшается.
Дифференциальное
уравнение свободно затухающих колебаний
линейной системы задаётся в виде:

,
где х – колеблющаяся величина, описывающая
тот или иной физический процесс,
β=b/2m=const
– коэффициент затухания, ω₀
– циклическая частота свободных
незатухающих колебаний той же колебательной
системы, т.е. при β =0 (при отсутствии
потерь энергии) называется собственной
частотой колебательной системы. Решение
дифференциального уравнения затухающих
элементов:

Сделаем

Подставляем
найденное вместе с выражением для х и
после сокращения на
. 1)Еслито решение этого Д/У имеет вид.
Начальная амплитуда колебаний А и
начальная фаза φ зависит от способа
возбуждения колебаний. Решением этого
уравнения являются затухающие колебания.
Периодом затухающих колебаний называется
промежуток времени между двумя последними
выражениями колебательной системы от
положения равновесия.
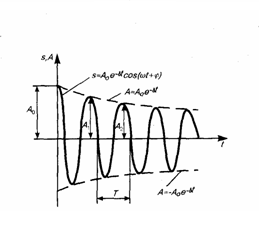ЕслиA(t)
и A(t+T)
– амплитуды двух последовательных
колебаний, соответствующих моментам
времени, отличающимся на период, то
отношение:
называется декрементом затухания, а
его логарифм

– логарифмическим
декрементом затухания; N_e
– число колебаний, совершаемых за время
уменьшения амплитуды в e
раз. Логарифмический декремент затухания
– постоянная для каждой колебательной
системы величина. 2) если
–
в этом случае понятие периода теряет
смысл- апериодический характер.