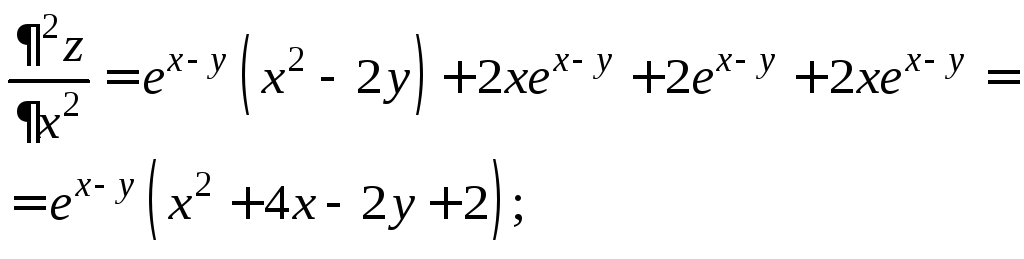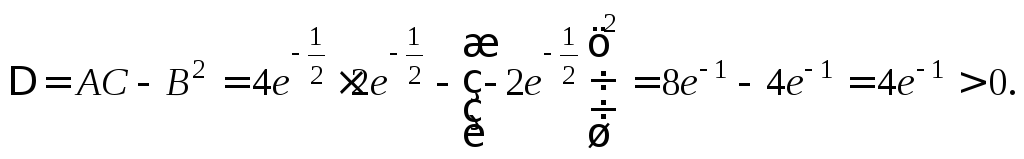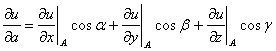Как найти длину вектора градиента

Градиент функции онлайн

Градиент функции – это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , – частные производные функции по переменным , , соответственно.

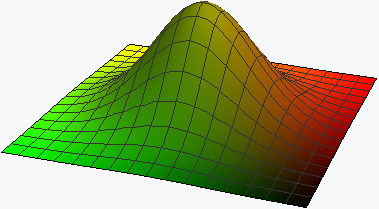
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Нахождение градиента вектор-функции

Дата публикации Oct 20, 2018

ВЧасть 1Нам поставили задачу: вычислить градиент этой функции потерь:

Чтобы найти градиент, мы должны найти производную функцию. ВЧасть 2мы научились вычислять частную производную функции по каждой переменной. Однако большинство переменных в этой функции потерь являются векторами. Возможность найти частную производную векторных переменных особенно важна, поскольку нейронная сеть работает с большими объемами данных. Векторные и матричные операции – это простой способ представления операций с таким большим количеством данных. Как именно вы можете найти градиент вектор-функции?

Градиент скалярной функции

Скажи, что у нас есть функция,f (x, y) = 3x²y, Наши частные производные:

Если мы организуем эти части в горизонтальный вектор, мы получимградиентизР (х, у), или∇ f (x, y):

6yxэто изменение вР (х, у)в отношении изменения вИкс, в то время как3x²это изменение вР (х, у)в отношении изменения вY,

Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию,g (x, y) = 2x + y⁸, Частные производные:

Таким образом, градиент g (x, y):

Представляющие функции

Когда у нас есть несколько функций с несколькими параметрами, часто полезно представлять их более простым способом. Мы можем объединить несколько параметров функций в один векторный аргумент,Иксэто выглядит следующим образом:

Следовательно,Р (х, у, г)станетF (x₁, x₂, x₃)который становитсяе (Икс).

Мы также можем объединить несколько функций в вектор, например так:

В настоящее время,у = F (X)гдеF (X)является вектором из [f₁ (Икс), f₂ (Икс), f₃ (Икс) . п (Икс)]

Для нашего предыдущего примера с двумя функциями,f (x, y) ⇒ f (Икс)а такжеg (x, y) ⇒ g (Икс).Здесь векторИкс= [x₁, x₂], гдеx₁ = х, а такжеx₂ = у, Чтобы упростить его еще больше, мы можем объединить наши функции: [f (Икс),г(Икс)] = [f₁ (Икс), f₂ (Иксзнак равноf (x) = y.

Зачастую количество функций и количество переменных будет одинаковым, поэтому для каждой переменной существует решение.

Градиент вектор-функции

Теперь, когда у нас есть две функции, как мы можем найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы переместимся из векторного исчисления в матричное исчисление. Эта матрица и организация градиентов нескольких функций с несколькими переменными, известна какМатрица Якобиана,

Есть несколько способов представления якобиана. Этот макет, где мы укладываем градиенты по вертикали, известен какмакет числителя, но другие документы будут использоватьрасположение знаменателя, который просто переворачивает его по диагонали:

Градиент функции идентичности

Давайте возьмем функцию идентичности,у = ф (х) = х, гдеFi (Икс) = xiи найдите его градиент:

Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложить их вертикально, чтобы создать якобиан тождественной функции:

Поскольку это функция идентичности, f₁ (Икс) = x₁, f₂ (Икс) = х₂ и тд. Следовательно,

Частичная производная функции по переменной, которой нет в функции, равна нулю. Например, частная производная 2x² по y равна 0. Другими словами,

Поэтому все, что не на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к себе равна 1. Например, частная производнаяИксв отношенииИксравен 1. Следовательно, якобиан становится:

Градиент комбинаций вектор-векторных функций

Элементарные бинарные операторыявляются операциями (такими как сложениевес+Иксиливес>Икскоторый возвращает вектор единиц и нулей), который применяет оператор последовательно, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второго элемента обоих векторов, чтобы получить второй элемент вывода… и так далее.

Эта статья представляет поэлементные бинарные операции с такими обозначениями:

Здесь ◯ означает любой поэлементный оператор (например, +), а не композицию функций.

Итак, как вы находите градиент поэлементной операции двух векторов?

Поскольку у нас есть два набора функций, нам нужны два якобиана, один из которых представляет градиент относительноИкси один по отношению квес:

Большинство арифметических операций нам понадобятся простые, поэтомуе (ш)часто просто векторвес, Другими словами,Fi (Wi) = Wi, Например, операцияW + хподходит к этой категории, так как она может быть представлена ​​каке (ж) + д (х)гдеfi (wi) + gi (xi) = wi + xi.

При этом условии каждый элемент в двух якобианах упрощается до:

На диагонали i = j, поэтому существует значение для частной производной. Вне диагонали, однако, i ≠ j, поэтому частные производные становятся равными нулю:

Мы можем представить это более кратко как:

Попробуем найти градиент функцииW + х, Мы знаем, что все вне диагонали равно 0. Значения частичных по диагонали относительновеса такжеИксявляются:

Итак, оба якобиана имеют диагональ 1. Это выглядит знакомо . это матрица тождеств!

Давайте попробуем это с умножением:ш * х, Значения частностей по диагонали относительновеса такжеИксявляются:

Следовательно, градиент по отношению квесизш * хявляетсяDiag (Икс)в то время как градиент по отношению кИксизш * хявляетсяDiag (вес).

Применяя те же шаги для вычитания и деления, мы можем суммировать все это:

Градиент векторных сумм

Одной из наиболее распространенных операций в глубоком обучении является операция суммирования. Как мы можем найти градиент функцииу = сумма (Икс)?

у = сумма (Икс)также может быть представлен как:

Следовательно, градиент может быть представлен как:

А так как частная производная функции по переменной, которой нет в функции, равна нулю, ее можно дополнительно упростить следующим образом:

Обратите внимание, что результатом является горизонтальный вектор.

Как насчет градиентау = сумма (Иксг)? Единственное отличие состоит в том, что мы умножаем каждый частный с константой, z:

Хотя это является производной по отношению кИкс, производная по скаляруZэто просто число:

Градиент комбинаций векторных функций правила цепочки

ВЧасть 2мы узнали о правилах цепей с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!

Давайте возьмем векторную функцию,Yзнак равное(Икс)и найти градиент. Давайте определим функцию как:

И то и другоеf₁ (х)а такжеf₂ (х)являются составными функциями. Введем промежуточные переменные дляf₁ (х)а такжеf₂ (х)и переписать нашу функцию:

Теперь мы можем использовать наше правило цепочки переменных, чтобы вычислить производную вектораY, Просто вычислите производнуюf₁ (х)а такжеf₂ (х)и поместите их один над другим:

Вуаля! У нас есть наш градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа в вектор. Есть ли способ представить правило цепи с несколькими переменными для векторов?

Прямо сейчас наш градиент вычисляется с помощью:

Обратите внимание, что первый член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₁надИкси второй член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₂надИкс Это как умножение матриц! Поэтому мы можем представить это как:

Давайте проверим наше новое представление правила цепочки векторов:

Мы получаем тот же ответ, что и скалярный подход! Если вместо одного параметраИксу нас есть векторный параметрИкснам просто нужно немного изменить наше правило, чтобы получить полное правило цепочки векторов:

В нашем примере выше,еэто чисто функцияг; то есть,фиявляется функциейсолдатно нетGJ(каждая функцияесоответствует ровно 1 функцииг),В этом случае все вне диагонали становится равным нулю, и:

Теперь у нас есть все части, которые мы находим в градиенте нейронной сети, с которой мы начали нашу серию:

Проверять, выписыватьсяЧасть 4чтобы узнать, как вычислить его производную!

Если вы еще этого не сделали, прочитайте части 1 и 2:

ЧитатьЧасть 4для грандиозного финала!

Скачать оригинал статьиВот,

Если вам понравилась эта статья, не забудьте оставить несколько хлопков! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения 🙂

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, – это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM 1 можно обозначить .

Функция u = f(M) при этом получит приращение

.

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

.

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Примеры нахождения производной по направлению

Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас – домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 – точка с координатами (3; 0) .

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере – в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M 0 :

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции

Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

Пример 4. Найти градиент функции в точке M 0 (2; 4;) .

Решение. Найдём частные производные функции в точке M 0 :

Следовательно, можем записать искомый градиент данной функции:

.

[spoiler title=”источники:”]

http://www.machinelearningmastery.ru/step-by-step-the-math-behind-neural-networks-d002440227fb/

http://function-x.ru/derivative_directional.html

[/spoiler]

Производной
функции
в точке
по направлению
называется предел

где

если предел
существует.

Если функция
дифференцируема, то производная по
направлению вычисляется по формуле

(18.31)

где
– направляющие косинусы вектора

В частности, если
– функция двух переменных, то формула
(18.31) производной по направлению примет
вид:

(18.32)

где
– угол между вектороми осьюОх.

Градиентомфункциив точкеназывается вектор

(18.33)

или, то же самое,

Связь между
градиентом функции и производной по
направлению устанавливает формула

где
– угол между векторамии

Градиент функции
указывает направление наибыстрейшего
возрастания функции. Наибольшее значение
производной
достигаемое в направление градиента,
равно

В
частности, если
– функция двух переменных, то

Пример
1. Найти
производную функции
в точкепо направлению вектораобразующего с положительным направлением
осиОх
угол

Решение.
Используя
формулу (18.32),
вычислим
частные производные функции z
в точке A:

Так
как
то

Пример
2. Найти
производную функции
в точкепо направлению к точке

Решение.
Найдем вектор

Его направляющие
косинусы равны:

Найдем
значения частных производных функции
u
в точке

Тогда
по формуле (18.31) получим:

Пример
3. Найти
длину и направление (указать направляющие
косинусы) градиента функции
в точке

Решение.
Вычислим
частные производные функции u
в точке М.

Используем
формулу (18.33) при условии, что частные
производные вычисляем в заданной точке

Тогда

Вычисляем
длину полученного вектора:

Используем
тот факт, что направляющие косинуса
равны координатам единичного вектора
направления, определяемого вектором
дроби. Поэтому

Задания

I уровень

1.1.Найдите
производную функциив точкепо направлению вектора

1)

2)

3)

4)

1.2.Найдите
производную функциив точкепо направлению вектора

1.3.Найдите
величину и направление градиента функциив точке

1)

2)

3)

4)

5)

II уровень

2.1.Найдите
производную указанной функции в точкепо направлению к точке

1)

2)

3)

4)

2.2.Найдите
величину и направление градиента функциизаданной неявно, в точке

1)

2)

3)

4)

2.3.Найдите
угол между градиентами функциив точкахи

2.4.Найдите
производную функциив точкев направленииперпендикулярном к линии уровня,
проходящей через эту точку.

III уровень

3.1. Найдите
градиент функциив точкахи

3.2.Определите,
в каких точках градиент функцииудовлетворяет условию:

1) параллелен оси
Оу;

2) перпендикулярен
оси Оу;

3) равен нулю.

3.3.Выясните,
в каких точках градиент функцииудовлетворяет условию:

1) перпендикулярен
прямой
2)
равен нулю.

3.4.Определите,
в каких точках выполнено равенствоесли

3.5.Найдите
градиент функциизаданной неявно уравнением:

1)
2)3)

3.6.Определите
направление наибыстрейшего возрастания
функции:

1)
2)

3)
4)

18.8. Экстремумы функций двух переменных

Функция
имеет в точкелокальный максимум (минимум),
если существует такая-окрестность
точкиМ₀, что для всех точекиз этой окрестности (отличных отМ₀)
выполняется неравенство

Максимум и минимум
функции называются ее экстремумами(локальными), а точкаМ₀, в
которой достигается экстремум, называетсяточкой экстремума.

Необходимое
условие экстремума: если
в точке
дифференцируемая функцияимеет экстремум, то ее частные производные
в этой точке равны нулю:

(18.34)

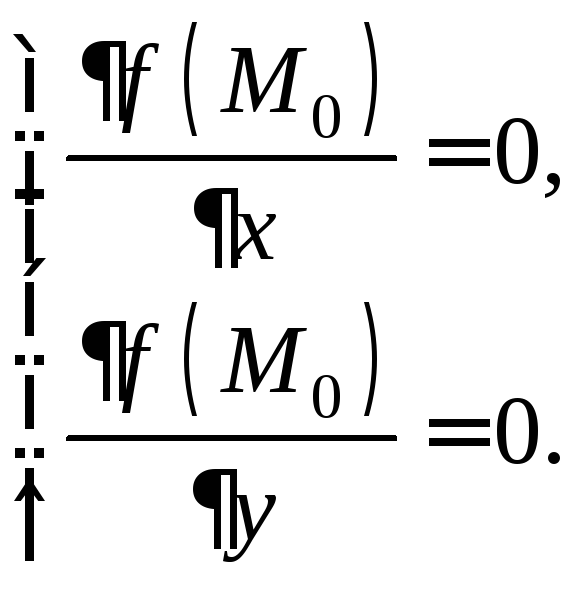
Точки, в которых
частные производные существуют и равны
нулю, называются стационарными.

Точки из области
определения функции, в которых частные
производные равны нулю или не существуют,
называются критическими точками.

Не всякая критическая
точка является точкой экстремума.

Достаточное
условие экстремума. Пусть– стационарная точка дважды непрерывно
дифференцируемой функцииОбозначим:

Тогда:

1) если
то функция имеет в точкеМ₀локальный экстремум (максимум прии минимум при);

2) если
то в точкеМ₀функция не имеет
экстремума;

3) если
то в точкеМ₀функция может
иметь локальный экстремум, а может и не
иметь его (нужны дополнительные
исследования).

Допустим, что
функция f(x;y) определена на
некотором множестве

Число Сназываютнаибольшим значением функции(глобальный максимум) на множестве
D, если

записывают так:

Число сназываютнаименьшим значением функции(глобальным минимумом) на множествеD, если

записывают так:

Теорема
Вейерштрасса. Непрерывная на
замкнутом ограниченном множествефункциядостигает на этом множестве своего
наибольшего и наименьшего значений.

Для нахождения
наибольшего и наименьшего значений
функции в области
нужно:

1) найти критические
точки функции, принадлежащие D, и
вычислить значение функции в них;

2) найти наибольшее
и наименьшее значения функции на границах
области

3) сравнить все
полученные значения функции и выбрать
из них наибольшее и наименьшее.

Если область
определения функции не является
замкнутой, то для нахождения наибольшего
и наименьшего значений функции необходимо:

1) найти критические
точки функции, принадлежащие D;

2) исследовать
найденные критические точки на экстремум
(локальный);

3) вычислить значения
функции в точках локального максимума
(минимума) и отобрать среди них наибольшее
(наименьшее).

Пример
1. Исследовать
на экстремум функцию

Решение.
Находим частные производные первого
порядка:

Приравниваем их
к нулю, чтобы найти стационарные точки:

Решая
систему уравнений, получим:
т. е.

Вычисляем
значения частных производных второго
порядка в точке М₀:

Тогда
Следовательно, в точкеэкстремума нет.

Пример
2. Найти
экстремум функции

Решение.
Частные
производные первого порядка:

Стационарные
точки:

Частные производные
второго порядка:

Тогда

Получаем:

Поскольку
то в точкефункция имеет минимум:

Пример
3. Найти
наибольшее и наименьшее значения функции
в областиограниченной прямыми

Решение.
1) Вычислим частные производные и найдем
критические точки:

Получим:
– критическая точка, принадлежащая
области

Вычислим в ней
значение функции:

2)
Исследуем функцию z
на границе области
(рис. 18.4).

Рис. 18.4

Уравнение
границы AB:
Подставляем число –3 вместох
в аналитическое задание функции:
где

Исследуем
полученную функцию, как функцию одной
переменной, на наибольшее значение.

Найдем критические
точки:

Получаем
– критическая точка, при этом

Вычисляем
значение функции в точке
и на концах отрезка:

Уравнение
границы BC:
На этом участке уравнение функции имеет
вид:где

Поскольку
то дляполучаем критическую точкуТогда

Уравнение
границы AC:
ТогдагдеКритическая точкапринадлежащая

Вычисляем
значение функции для

3)
Из всех полученных значений z
выбираем наименьшее и наибольшее:

Задания

Соседние файлы в папке Часть 3

• #
• #
• #
• #
• #
• #
• #
• #

Градиент функции

Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.

Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:

• нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
• вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
• нахождение полного дифференциала функции.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Решение со всеми исходными формулами сохраняется в формате Word.

Полный дифференциал для функции двух переменных: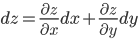

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

Алгоритм нахождения градиента

1. Вычисление частных производных по формуле:

   

2. Вычисление частных производных в точке A.
3. Нахождение направляющих углов вектора a.
4. Вычисление производной в точке A по направлению вектора a по формуле;

   

5. Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.

Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле

∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},

где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).

Иногда градиент обозначается так: grad⁡F(x,y,z)operatorname{grad} F(x,y,z).

Градиент функции в данной точке показывает направление наибольшего роста функции.

Пример 1

Найти градиент функции F(x,y,z)=ln⁡(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).

Вычислим частные производные:
∂F∂x=∂∂xln⁡(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},

∂F∂y=∂∂yln⁡(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},

∂F∂z=∂∂zln⁡(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.

Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):

∇F(M)=17  i+27  j+37  k=17  OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.

Производная по направлению

Пусть FF – функция на плоскости или в пространстве.

Производной функции FF по направлению вектора amathbf{a} в точке MM называется число

∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},

если производная в правой части существует.

Пример 2

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).

Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):

F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.

Длина вектора amathbf{a}:

∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.

Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}

Выражение производной по направлению через градиент

Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства

F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)

следует, что

ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).

Таким образом,

∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.

Пример 2′2′

Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.

Частные производные:

∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,

∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,

∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.

Градиент:

∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.

Скалярное произведение:

(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.

Производная по направлению:

∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.

Тест по теме “Градиент функции. Производная по направлению”

17.04.2020

Как найти градиент функции в точке?

Если для каждой пары (x,y) значений двух независимых переменных из некоторой области ставится в соответствие определенное значение z, то говорят, что z является функцией двух переменных (x,y). Обозначение: z=f(x,y).

Рассмотрим функцию z=f(x,y), которая определена в некоторой области в пространстве Oxy.

Градиент заданной функции

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке frac{partial z}{partial x} ;frac{partial z}{partial y}. Градиентом заданной функции z=f(x,y) называется вектор overrightarrow{gradz} следующего вида:

• [overrightarrow{gradz} =frac{partial z}{partial x} cdot overrightarrow{i} +frac{partial z}{partial y} cdot overrightarrow{j} .]

Пусть в некотором скалярном поле $z=z(x,y)$ определено поле градиентов:

• [overrightarrow{gradz} =frac{partial z}{partial x} cdot overrightarrow{i} +frac{partial z}{partial y} cdot overrightarrow{j} .]

Производная frac{partial z}{partial s} по направлению заданного вектора overrightarrow{s} равна проекции вектора градиента overrightarrow{gradz} на заданный вектор overrightarrow{s}.

Теорема 1

Для функции двух переменных вектор overrightarrow{gradz} направлен перпендикулярно к линии уровня z(x,y)=c, которая лежит в плоскости Oxy и проходит через соответствующую точку.

Пример 1

Определить градиент заданной функции [z=x+y^{2} ] в точке M(1;2). Вычислить left(|overrightarrow{gradz} |
ight)_{M}.

Решение:

[left(overrightarrow{gradz} ight)_{M} =left(frac{partial z}{partial x} ight)_{M} cdot overrightarrow{i} +left(frac{partial z}{partial y} ight)_{M} cdot overrightarrow{j} .]

[frac{partial z}{partial x} =1;frac{partial z}{partial y} =2y.] [frac{partial z}{partial x} =1;frac{partial z}{partial y} =2cdot 2=4.] [left(overrightarrow{gradz} ight)_{M} =overrightarrow{i} +4cdot overrightarrow{j} ] [left(|overrightarrow{gradz} |ight)_{M} =sqrt{1^{2} +4^{2} } =sqrt{1+16} =sqrt{17} .]

Если для каждой тройки (x,y,z) значений трех независимых переменных из некоторой области ставится в соответствие определенное значение w, то говорят, что w является функцией трех переменных (x,y,z) в данной области.

Обозначение: w=f(x,y,z). Рассмотрим функцию w=f(x,y,z), которая определена в некоторой области в пространстве Oxyz.

Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке frac{partial z}{partial x}; frac{partial z}{partial y}.

Градиентом заданной функции w=f(x,y,z) называется вектор overrightarrow{gradw} следующего вида:

[overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .]

Теорема 2

Пусть в некотором скалярном поле w=f(x,y,z) определено поле градиентов:

[overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .]

Производная frac{partial w}{partial s} по направлению заданного вектора overrightarrow{s} равна проекции вектора градиента overrightarrow{gradw} на заданный вектор overrightarrow{s}.

Пример 2

Определить градиент заданной функции

Решение:

[w=x^{2} +2y^{2} +2z.] [overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .] [frac{partial w}{partial x} =2x;frac{partial w}{partial y} =4y;frac{partial w}{partial z} =2.] [overrightarrow{gradw} =2xcdot overrightarrow{i} +4ycdot overrightarrow{j} +2cdot overrightarrow{k} .]

Перечислим некоторые свойства градиента:

• Производная заданной функции в заданной точке по направлению некоторого вектора overrightarrow{s} имеет наибольшее значение, если направление данного вектора overrightarrow{s} совпадает с направлением градиента. При этом данное наибольшее значение производной совпадает с длиной вектора градиента, т.е. |overrightarrow{gradw} |.
• Производная заданной функции по направлению вектора, который перпендикулярен к вектору градиента, т.е. overrightarrow{gradw}, равна 0. Так как varphi =frac{pi }{2}, то cos varphi =0; следовательно, frac{partial w}{partial s} =|overrightarrow{gradw} |cdot cos varphi =0.

Источник: https://spravochnick.ru/matematika/funkcii_neskolkih_peremennyh/gradient_zadannoy_funkcii/

Оценка статьи:

(нет голосов)

Загрузка…