Есть список, например:
["2 -1 5 4"]
Это координаты точек вектора, соответственно x1,y1,x2,y2. Нужно найти длину вектора образованного этими точками.
Подскажите более “питоновский” способ решения такой задачи. Как правильно вырвать значения из этой строки, чтобы потом всё посчитать?
На то, что в списке просто одна строка, не обращайте внимания, так и должно быть. 🙂
задан 13 ноя 2018 в 15:19
9
Решение с использованием модуля Pandas:
import pandas as pd # pip install pandas
# читаем файл в pandas.DataFrame
df = pd.read_csv(filename, delim_whitespace=True, header=None, names=['x1','y1','x2','y2'])
получили:
In [373]: df
Out[373]:
x1 y1 x2 y2
0 2 -1 5 4
1 1 2 3 4
2 10 3 18 1
считаем расстояния между точками для каждой строки:
df = df.eval("dist = ((x1-x2)**2 + (y1-y2)**2)**0.5")
результат:
In [375]: df
Out[375]:
x1 y1 x2 y2 dist
0 2 -1 5 4 5.830952
1 1 2 3 4 2.828427
2 10 3 18 1 8.246211
ответ дан 13 ноя 2018 в 15:40
![]()
Можно при помощи регулярных выражений сделать:
import re
map(int, re.findall(r'd+|-d+', l[0])) # вернёт [2, -1, 5, 4]
ответ дан 13 ноя 2018 в 15:30
nick_gabpenick_gabpe
3,8434 золотых знака20 серебряных знаков37 бронзовых знаков
In Python Numpy you can get array length/size using numpy.ndarray.size and numpy.ndarray.shape properties. The size property gets the total number of elements in a NumPy array. The shape property returns a tuple in (x, y).
You can get the length of the multi-dimensional array with the shape property in Python. In this article, we’ll explain several ways of how to get Numpy array length with examples by using properties like numpy.ndarray.size and numpy.ndarray.shape with examples.
If you are in a hurry, below are some quick examples of getting Python NumPy array size.
# Below are a quick example
# Example 1: Use numpy.size Property
arr = np.array([1,3,6,9,12,15,20,22,25])
print(arr.size)
# Example 2: Using on 2-d array
arr = np.array([[1,3,6],[9,12,15],[20,22,25]])
print(arr.size)
# Example 3: Use numpy.shape property
arr = np.array([[1,3,6],[9,12,15],[20,22,25]])
print(arr.shape)
2. Use NumPy.size to Get Length
You can use ndarray.size property to get the total number of elements (length) in a NumPy array. Let’s create a NumPy array and use this to get the number of elements from one-dimensional arrays.
import numpy as np
# Example 1: Use numpy.size Property
arr = np.array([1,3,6,9,12,15,20,22,25])
print(arr.size)
# OutPut
#9
In the below code, you get the number of elements in the multi-dimensional array with the ndarray.size property in Python. It also gives us the value 9 because the total number of elements is the same as in the previous example. This is the reason why this method is not suitable for multi-dimensional arrays.
# Example 2: Use numpy.size property to get length of a NumPy array
array = np.array([[1,3,6],[9,12,15],[20,22,25]])
print(array.size)
# OutPut
#9
3. Use NumPy.shape to get Length
So for multi-dimensional NumPy arrays use ndarray.shape function which returns a tuple in (x, y), where x is the number of rows and y is the number of columns in the array. You can now find the total number of elements by multiplying the values in the tuple with each other. This method is preferred over the previous method because it gives us the number of rows and columns.
# Example 3: Use numpy.shape property
arr = np.array([[1,3,6],[9,12,15],[20,22,25]])
print(arr.shape)
# Output
#(3, 3)
4. Conclusion
In this article, I have explained how to get Python Numpy array length/size or shape using ndarray.shape, ndarray.size properties with examples. By using the size property you can get the size of the array however it is not suitable to get the length of the multi-dimensional array. In order to get the multi-dimensional array size use the shape property which returns the tuple(x,y)
Happy Learning!!
Related Articles
- How to convert NumPy array to list?
- How to Slice NumPy Array?
- Python NumPy Array Reshape
- How to Get NumPy Array Shape?
- How to create NumPy array in different ways ?
- NumPy fill() Function with Examples
- NumPy Array Addition
- NumPy Element Wise Multiplication
References
- https://numpy.org/doc/stable/reference/generated/numpy.ndarray.size.html
Работа с векторами в Python с помощью NumPy
В этом уроке мы узнаем, как создать вектор с помощью библиотеки Numpy в Python. Мы также рассмотрим основные операции с векторами, такие как сложение, вычитание, деление и умножение двух векторов, векторное точечное произведение и векторное скалярное произведение.
Что такое вектор в Python?
Вектор известен как одномерный массив. Вектор в Python – это единственный одномерный массив списков, который ведет себя так же, как список Python. Согласно Google, вектор представляет направление, а также величину; особенно он определяет положение одной точки в пространстве относительно другой.
Векторы очень важны в машинном обучении, потому что у них есть величина, а также особенности направления. Давайте разберемся, как мы можем создать вектор на Python.
Создание вектора в Python
Модуль Python Numpy предоставляет метод numpy.array(), который создает одномерный массив, то есть вектор. Вектор может быть горизонтальным или вертикальным.
Вышеупомянутый метод принимает список в качестве аргумента и возвращает numpy.ndarray.
Давайте разберемся в следующих примерах.
Пример – 1: горизонтальный вектор
Пример – 2: Вертикальный вектор
Базовые операции вектора Python
После создания вектора мы теперь будем выполнять арифметические операции над векторами.
Ниже приведен список основных операций, которые мы можем производить с векторами:
- сложение;
- вычитание;
- умножение;
- деление;
- точечное произведение;
- скалярные умножения.
Сложение двух векторов
В векторном сложении это происходит поэлементно, что означает, что сложение будет происходить поэлементно, а длина будет такой же, как у двух аддитивных векторов.
Давайте разберемся в следующем примере.
Вычитание
Вычитание векторов выполняется так же, как и сложение, оно следует поэлементному подходу, и элементы вектора 2 будут вычтены из вектора 1. Давайте разберемся в следующем примере.
Умножение векторов
Элементы вектора 1 умножаются на вектор 2 и возвращают векторы той же длины, что и векторы умножения.
Умножение производится следующим образом.
Первый элемент вектора 1 умножается на первый элемент соответствующего вектора 2 и так далее.
Операция деления двух векторов
В операции деления результирующий вектор содержит значение частного, полученное при делении двух элементов вектора.
Давайте разберемся в следующем примере.
Как видно из вышеприведенного вывода, операция деления вернула частное значение элементов.
Векторное точечное произведение
Векторное скалярное произведение выполняется между двумя последовательными векторами одинаковой длины и возвращает единичное скалярное произведение. Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.
Давайте разберемся в следующем примере.
Векторно-скалярное умножение
В операции скалярного умножения; мы умножаем скаляр на каждую компоненту вектора. Давайте разберемся в следующем примере.
В приведенном выше коде скалярное значение умножается на каждый элемент вектора в порядке s * v =(s * v1, s * v2, s * v3).
Операции над векторами в numpy
Рассмотрим некоторые общие функции линейной алгебры и их применение на чистом Python и numpy. Все примеры — на Jupyter Notebook.
Списки в Python не являются векторами, по умолчанию над ними нельзя производить поэлементные операции.
В Python необходимо определять собственные функции, чтобы оперировать списками как векторами. Для сравнения: в numpy для аналогичных операций достаточно одной строки кода.
Сложение векторов
Но, конечно, в numpy это можно сделать с помощью оператора + на numpy-массивах или с помощью метода sum() .
Вычитание векторов
Скалярное умножение
Среднее значение вектора
Скалярное произведение
Сумма квадратов
Величина вектора
Расстояние между двумя векторами
На заметку
В ряде рассмотренных примеров используется sum() . Чем отличается встроенная Python-функция sum() от numpy.sum() ? Например тем, что numpy.sum() быстрее обрабатывает numpy-массивы, но медленнее Python-списки.
Проверим в Python 2.7.2 и Numpy 1.6.1:
Результат при x = range(1000) :
Результат при x = np.random.standard_normal(1000) :
Согласитесь, имеет смысл учитывать контекст использования.
В основе статьи — материал Бена Алекса Кина. Мой небольшой вклад — перевод, идиоматический код numpy-примеров и дополнительные пояснения.
Векторы в Python
В простом смысле вектор можно рассматривать, как одномерный массив. Что касается Python, вектор – это одномерный массив списков. Он занимает элементы таким же образом, как и список Python.
Давайте теперь разберемся с созданием вектора в Python.
Создание вектора
Модуль NumPy в Python используется для создания вектора. Мы используем метод numpy.array() для создания одномерного массива, то есть вектора.
Пример 1: горизонтальный вектор.
Пример 2: вертикальный вектор.
Основные операции с вектором
Создав вектор, давайте теперь выполним некоторые базовые операции с этими векторами!
Вот список основных операций, которые можно выполнять с вектором:
- сложение;
- вычитание;
- умножение;
- деление;
- скалярное произведение и т.д.
1. Выполнение операции сложения в векторе
Ниже мы выполнили операцию сложения векторов над векторами. Операция сложения будет выполняться element-wise manner, т.е. поэлементно, и, кроме того, результирующий вектор будет иметь такую же длину, что и два аддитивных вектора.
2. Выполнение вычитания двух векторов
Аналогичным образом, при вычитании также будет применяться поэлементный метод, и в дальнейшем элементы вектора 2 будут вычитаться из вектора 1.
Давайте посмотрим на его реализацию.
3. Выполнение умножения двух векторов
При умножении вектора элементы вектора 1 умножаются на элементы вектора 2, а вектор произведения имеет ту же длину, что и векторы умножения.
Попробуем представить себе операцию умножения:
x = [10,20] и y = [1,2] — два вектора. Таким образом, вектор произведения будет v [],
v [0] = x [0] * y [0] v [1] = x [1] * y [1]
Взгляните на приведенный ниже код:
4. Выполнение операции деления
При делении результирующий вектор является значениями частного после выполнения операции деления над двумя векторами.
Для лучшего понимания рассмотрим приведенный ниже пример.
x = [10,20] и y = [1,2] – два вектора. Таким образом, результирующий вектор v будет таким:
v [0] = x [0] / y [0] v [1] = x [1] / y [1].
Давайте теперь реализуем вышеуказанную концепцию.
5. Векторное точечное произведение
В векторном скалярном произведении мы поэлементно производим суммирование произведения двух векторов.
[spoiler title=”источники:”]
http://zyatev.ru/python/operatsii-nad-vektorami-v-numpy
http://pythonim.ru/osnovy/vektory-v-python
[/spoiler]
Содержание
- NumPy: матрицы и операции над ними
- 1. Создание матриц
- 2. Индексирование
- 3. Векторы, вектор-строки и вектор-столбцы
- 4. Datatypes
- 5. Математические операции
- 6. Умножение матриц и столбцов
- 7. Объединение массивов
- Задания: (Блок 1)
- Задание 1:
- Задание 2:
- Задания: (Блок 1)
- 8. Транспонирование матриц
- 9. Определитель матрицы
- 10. Ранг матрицы
- 11. Системы линейных уравнений
- 12. Обращение матриц
- 13. Собственные числа и собственные вектора матрицы
- 14. Расстояния между векторами
- p-норма
- ℓ1 норма
- ℓ2 норма
- 15. Расстояния между векторами
- 16. Скалярное произведение и угол между векторами
- 17. Комплексные числа в питоне
- Задания: (Блок 2)
- Задание 3:
- Задания: (Блок 2)
NumPy: матрицы и операции над ними
Ссылка на jupyter notebook
В этом ноутбуке из сторонних библиотек нам понадобится только NumPy.
Для удобства импортируем ее под более коротким именем:
import numpy as np
1. Создание матриц
Приведем несколько способов создания матриц в NumPy.
Самый простой способ — с помощью функции
numpy.array(list, dtype=None, …).
В качестве первого аргумента ей надо передать итерируемый объект,
элементами которого являются другие итерируемые объекты одинаковой длины
и содержащие данные одинакового типа.
Второй аргумент является опциональным и определяет тип данных матрицы.
Его можно не задавать, тогда тип данных будет определен из типа
элементов первого аргумента. При задании этого параметра будет
произведена попытка приведения типов.
Например, матрицу из списка списков целых чисел можно создать следующим
образом:
a = np.array([1, 2, 3]) # Создаем одномерный массив print(type(a)) # Prints "<class 'numpy.ndarray'>" print(a.shape) # Prints "(3,)" - кортеж с размерностями print(a[0], a[1], a[2]) # Prints "1 2 3" a[0] = 5 # Изменяем значение элемента массива print(a) # Prints "[5, 2, 3]" b = np.array([[1,2,3],[4,5,6]]) # Создаем двухмерный массив print(b.shape) # Prints "(2, 3)" print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4" print(np.arange(1, 5)) #Cоздает вектор с эелементами от 1 до 4
<class 'numpy.ndarray'> (3,) 1 2 3 [5 2 3] (2, 3) 1 2 4 [1 2 3 4]
matrix = np.array([[1, 2, 3], [2, 5, 6], [6, 7, 4]]) print ("Матрица:n", matrix)
Матрица: [[1 2 3] [2 5 6] [6 7 4]]
Второй способ создания — с помощью встроенных функций
numpy.eye(N, M=None, …), numpy.zeros(shape, …),
numpy.ones(shape, …).
Первая функция создает единичную матрицу размера N×M;
если M не задан, то M = N.
Вторая и третья функции создают матрицы, состоящие целиком из нулей или
единиц соответственно. В качестве первого аргумента необходимо задать
размерность массива — кортеж целых чисел. В двумерном случае это набор
из двух чисел: количество строк и столбцов матрицы.
Примеры:
b = np.eye(5) print ("Единичная матрица:n", b)
Единичная матрица: [[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]]
c = np.ones((7, 5)) print ("Матрица, состоящая из одних единиц:n", c)
Матрица, состоящая из одних единиц: [[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
d = np.full((2,2), 7) # Создает матрицу (1, 2) заполненую заданным значением print(d) # Prints "[[ 7. 7.] # [ 7. 7.]]" e = np.random.random((2,2)) # Создает еденичную матрицу (2, 2) заполненую случаными числами (0, 1) print(e) # Might print "[[ 0.91940167 0.08143941] # [ 0.68744134 0.87236687]]"
[[7 7] [7 7]] [[0.25744383 0.48056466] [0.13767881 0.40578168]]
Обратите внимание: размерность массива задается не двумя аргументами
функции, а одним — кортежем!
Вот так — np.ones(7, 5) — создать массив не получится, так как
функции в качестве параметра shape передается 7, а не кортеж
(7, 5).
И, наконец, третий способ — с помощью функции
numpy.arange([start, ]stop, [step, ], …), которая создает
одномерный массив последовательных чисел из промежутка
[start, stop) с заданным шагом step, и метода
array.reshape(shape).
Параметр shape, как и в предыдущем примере, задает размерность
матрицы (кортеж чисел). Логика работы метода ясна из следующего примера:
v = np.arange(0, 24, 2) print ("Вектор-столбец:n", v)
Вектор-столбец: [ 0 2 4 6 8 10 12 14 16 18 20 22]
d = v.reshape((3, 4)) print ("Матрица:n", d)
Матрица: [[ 0 2 4 6] [ 8 10 12 14] [16 18 20 22]]
Более подробно о том, как создавать массивы в NumPy, см.
документацию.
2. Индексирование
Для получения элементов матрицы можно использовать несколько способов.
Рассмотрим самые простые из них.
Для удобства напомним, как выглядит матрица d:
print ("Матрица:n", d)
Матрица: [[ 0 2 4 6] [ 8 10 12 14] [16 18 20 22]]
Элемент на пересечении строки i и столбца j можно
получить с помощью выражения array[i, j].
Обратите внимание: строки и столбцы нумеруются с нуля!
print ("Второй элемент третьей строки матрицы:", d[2, 1])
Второй элемент третьей строки матрицы: 18
Из матрицы можно получать целые строки или столбцы с помощью выражений
array[i, :] или array[:, j] соответственно:
print ("Вторая строка матрицы d:n", d[1, :]) print ("Четвертый столбец матрицы d:n", d[:, 3])
Вторая строка матрицы d: [ 8 10 12 14] Четвертый столбец матрицы d: [ 6 14 22]
Еще один способ получения элементов — с помощью выражения
array[list1, list2], где list1, list2 —
некоторые списки целых чисел. При такой адресации одновременно
просматриваются оба списка и возвращаются элементы матрицы с
соответствующими координатами. Следующий пример более понятно объясняет
механизм работы такого индексирования:
print ("Элементы матрицы d с координатами (1, 2) и (0, 3):n", d[[1, 0], [2, 3]])
Элементы матрицы d с координатами (1, 2) и (0, 3): [12 6]
# Slicing # Создадим матрицу (3, 4) # [[ 1 2 3 4] # [ 5 6 7 8] # [ 9 10 11 12]] a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) # Используя слайсинг, созадим матрицу b из элементов матрицы а # будем использовать 0 и 1 строку, а так же 1 и 2 столебц # [[2 3] # [6 7]] b = a[:2, 1:3] print(b) # ОБРАТИТЕ ВНИМАНИЕ НА ИЗМЕНЕНИЕ ИСХОДОЙ МАТРИЦЫ print(a[0, 1]) # Prints "2" b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1] print(a[0, 1]) # Prints "77"
[[2 3] [6 7]] 2 77
# Integer array indexing a = np.array([[1,2], [3, 4], [5, 6]]) print(a) print() # Пример Integer array indexing # В результате получится массив размерности (3,) # Обратите внимание, что до запятой идут индексы строк, после - столбцов print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]" print() # По-другому пример можно записать так print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
[[1 2] [3 4] [5 6]] [1 4 5] [1 4 5]
Примеры использования слайсинга:
# Создадим новый маассив, из которого будем выбирать эллементы a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) print(a) # prints "array([[ 1, 2, 3], # [ 4, 5, 6], # [ 7, 8, 9], # [10, 11, 12]])" # Создадим массив индексов b = np.array([0, 2, 0, 1]) # Выберем из каждой строки элемент с индексом из b (индекс столбца берется из b) print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]" print() # Добавим к этим элементам 10 a[np.arange(4), b] += 10 print(a) # prints "array([[11, 2, 3], # [ 4, 5, 16], # [17, 8, 9], # [10, 21, 12]])
[[ 1 2 3] [ 4 5 6] [ 7 8 9] [10 11 12]] [ 1 6 7 11] [[11 2 3] [ 4 5 16] [17 8 9] [10 21 12]]
a = np.array([[1,2], [3, 4], [5, 6]]) bool_idx = (a > 2) # Найдем эллементы матрицы a, которые больше 2 # В результате получим матрицу b, такой же размерности, как и a print(bool_idx) # Prints "[[False False] print() # [ True True] # [ True True]]" # Воспользуемся полученным массивом для создания нового массива, ранга 1 print(a[bool_idx]) # Prints "[3 4 5 6]" # Аналогично print(a[a > 2]) # Prints "[3 4 5 6]"
[[False False] [ True True] [ True True]] [3 4 5 6] [3 4 5 6]
#Помните, что вы можете пользоваться сразу несколькими типами индексирования a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) row_r1 = a[1, :] row_r2 = a[1:2, :] print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)" print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
[5 6 7 8] (4,) [[5 6 7 8]] (1, 4)
Более подробно о различных способах индексирования в массивах см.
документацию.
3. Векторы, вектор-строки и вектор-столбцы
Следующие два способа задания массива кажутся одинаковыми:
a = np.array([1, 2, 3]) b = np.array([[1], [2], [3]])
Однако, на самом деле, это задание одномерного массива (то есть
вектора) и двумерного массива:
print ("Вектор:n", a) print ("Его размерность:n", a.shape) print ("Двумерный массив:n", b) print ("Его размерность:n", b.shape)
Вектор: [1 2 3] Его размерность: (3,) Двумерный массив: [[1] [2] [3]] Его размерность: (3, 1)
Обратите внимание: вектор (одномерный массив) и вектор-столбец
или вектор-строка (двумерные массивы) являются различными объектами в
NumPy, хотя математически задают один и тот же объект. В случае
одномерного массива кортеж shape состоит из одного числа и имеет
вид (n,), где n — длина вектора. В случае двумерных
векторов в shape присутствует еще одна размерность, равная
единице.
В большинстве случаев неважно, какое представление использовать, потому
что часто срабатывает приведение типов. Но некоторые операции не
работают для одномерных массивов. Например, транспонирование (о нем
пойдет речь ниже):
a = a.T b = b.T
print ("Вектор не изменился:n", a) print ("Его размерность также не изменилась:n", a.shape) print ("Транспонированный двумерный массив:n", b) print ("Его размерность изменилась:n", b.shape)
Вектор не изменился: [1 2 3] Его размерность также не изменилась: (3,) Транспонированный двумерный массив: [[1 2 3]] Его размерность изменилась: (1, 3)
4. Datatypes
Все элементы в массиве numpy принадлежат одному типу. В этом плане
массивы ближе к C, чем к привычным вам листам питона. Numpy имеет
множество встренных типов, подходящих для решения большинства задач.
x = np.array([1, 2]) # Автоматический выбор типа print(x.dtype) # Prints "int64" x = np.array([1.0, 2.0]) # Автоматический выбор типа print(x.dtype) # Prints "float64" x = np.array([1, 2], dtype=np.int64) # Принудительное выставление типа print(x.dtype) # Prints "int64"
int32 float64 int64
5. Математические операции
К массивам (матрицам) можно применять известные вам математические
операции. Следут понимать, что при этом у элементов должны быть схожие
размерности. Поведение в случае не совпадения размерностей хорошо
описанно в документации numpy.
x = np.array([[1,2],[3,4]], dtype=np.float64) y = np.array([[5,6],[7,8]], dtype=np.float64) arr = np.array([1, 2])
# Сложение происходит поэлеметно # [[ 6.0 8.0] # [10.0 12.0]] print(x + y) print() print(np.add(x, y)) print('С числом') print(x + 1) print('C массивом другой размерности') print(x + arr)
[[ 6. 8.] [10. 12.]] [[ 6. 8.] [10. 12.]] С числом [[2. 3.] [4. 5.]] C массивом другой размерности [[2. 4.] [4. 6.]]
# Вычитание print(x - y) print(np.subtract(x, y))
[[-4. -4.] [-4. -4.]] [[-4. -4.] [-4. -4.]]
# Деление # [[ 0.2 0.33333333] # [ 0.42857143 0.5 ]] print(x / y) print(np.divide(x, y))
[[0.2 0.33333333] [0.42857143 0.5 ]] [[0.2 0.33333333] [0.42857143 0.5 ]]
# Другие функции # [[ 1. 1.41421356] # [ 1.73205081 2. ]] print(np.sqrt(x))
[[1. 1.41421356] [1.73205081 2. ]]
6. Умножение матриц и столбцов
Напоминание теории. Операция умножения определена для двух
матриц, таких что число столбцов первой равно числу строк второй.
Пусть матрицы A и B таковы, что
A ∈ ℝn×k и
B ∈ ℝk×m. Произведением матриц
A и B называется матрица C, такая что
cij = ∑kr = 1airbrj, где cij —
элемент матрицы C, стоящий на пересечении строки с номером
i и столбца с номером j.
В NumPy произведение матриц вычисляется с помощью функции
numpy.dot(a, b, …) или с помощью метода
array1.dot(array2), где array1 и array2 —
перемножаемые матрицы.
a = np.array([[1, 0], [0, 1]]) b = np.array([[4, 1], [2, 2]]) r1 = np.dot(a, b) r2 = a.dot(b)
print ("Матрица A:n", a) print ("Матрица B:n", b) print ("Результат умножения функцией:n", r1) print ("Результат умножения методом:n", r2)
Матрица A: [[1 0] [0 1]] Матрица B: [[4 1] [2 2]] Результат умножения функцией: [[4 1] [2 2]] Результат умножения методом: [[4 1] [2 2]]
Матрицы в NumPy можно умножать и на векторы:
c = np.array([1, 2]) r3 = b.dot(c)
print ("Матрица:n", b) print ("Вектор:n", c) print ("Результат умножения:n", r3)
Матрица: [[4 1] [2 2]] Вектор: [1 2] Результат умножения: [6 6]
Обратите внимание: операция * производит над матрицами
покоординатное умножение, а не матричное!
r = a * b
print ("Матрица A:n", a) print ("Матрица B:n", b) print ("Результат покоординатного умножения через операцию умножения:n", r)
Матрица A: [[1 0] [0 1]] Матрица B: [[4 1] [2 2]] Результат покоординатного умножения через операцию умножения: [[4 0] [0 2]]
Более подробно о матричном умножении в NumPy см.
документацию.
7. Объединение массивов
Массивы можно Объединенять. Есть горизонтальное и вертикальное
объединение.
a = np.floor(10*np.random.random((2,2))) b = np.floor(10*np.random.random((2,2))) print(a) print(b) print() print(np.vstack((a,b))) print() print(np.hstack((a,b)))
[[4. 0.] [1. 4.]] [[9. 7.] [2. 6.]] [[4. 0.] [1. 4.] [9. 7.] [2. 6.]] [[4. 0. 9. 7.] [1. 4. 2. 6.]]
Массивы можно переформировать при помощи метода, который задает новый
многомерный массив. Следуя следующему примеру, мы переформатируем
одномерный массив из десяти элементов во двумерный массив, состоящий из
пяти строк и двух столбцов:
a = np.array(range(10), float) print(a) print() # Превратим в матрицу a = a.reshape((5, 2)) print(a) print() # Вернем обратно print(a.flatten()) # Другой вариант print(a.reshape((-1))) # Превратим в марицу (9, 1) print(a.reshape((-1, 1))) # Превратим в марицу (1, 9) print(a.reshape((1, -1)))
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [[0. 1.] [2. 3.] [4. 5.] [6. 7.] [8. 9.]] [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [[0.] [1.] [2.] [3.] [4.] [5.] [6.] [7.] [8.] [9.]] [[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]]
Задания: (Блок 1)
Задание 1:
Решите без использования циклов средставми NumPy (каждый пункт решается
в 1-2 строчки)
- Создайте вектор с элементами от 12 до 42
- Создайте вектор из нулей длины 12, но его пятый елемент должен быть равен 1
- Создайте матрицу (3, 3), заполненую от 0 до 8
- Найдите все положительные числа в np.array([1,2,0,0,4,0])
- Умножьте матрицу размерности (5, 3) на (3, 2)
- Создайте матрицу (10, 10) так, чтобы на границе были 0, а внтури 1
- Создайте рандомный вектор и отсортируйте его
- Каков эквивалент функции enumerate для numpy массивов?
- *Создайте рандомный вектор и выполните нормализацию столбцов (из каждого столбца вычесть среднее этого столбца, из каждого столбца вычесть sd этого столбца)
- *Для заданного числа найдите ближайший к нему элемент в векторе
- *Найдите N наибольших значений в векторе
# ваш код здесь
Задание 2:
Напишите полностью векторизованный вариант
Дан трёхмерный массив, содержащий изображение, размера (height, width,
numChannels), а также вектор длины numChannels. Сложить каналы
изображения с указанными весами, и вернуть результат в виде матрицы
размера (height, width). Считать реальное изображение можно при помощи
функции
scipy.misc.imread
(если изображение не в формате png,
установите пакет pillow:
conda install pillow
). Преобразуйте
цветное изображение в оттенки серого, использовав коэффициенты
np.array([0.299, 0.587, 0.114]).
# ваш код здесь
8. Транспонирование матриц
Напоминание теории. Транспонированной матрицей AT
называется матрица, полученная из исходной матрицы A заменой
строк на столбцы. Формально: элементы матрицы AT определяются
как aTij = aji, где aTij — элемент
матрицы AT, стоящий на пересечении строки с номером i
и столбца с номером j.
В NumPy транспонированная матрица вычисляется с помощью функции
numpy.transpose() или с помощью метода array.T, где
array — нужный двумерный массив.
a = np.array([[1, 2], [3, 4]]) b = np.transpose(a) c = a.T
print ("Матрица:n", a) print ("Транспонирование функцией:n", b) print ("Транспонирование методом:n", c)
Матрица: [[1 2] [3 4]] Транспонирование функцией: [[1 3] [2 4]] Транспонирование методом: [[1 3] [2 4]]
См. более подробно о
numpy.transpose()
и
array.T
в NumPy.
В следующих разделах активно используется модуль numpy.linalg,
реализующий некоторые приложения линейной алгебры. Более подробно о
функциях, описанных ниже, и различных других функциях этого модуля можно
посмотреть в его
документации.
9. Определитель матрицы
Напоминание теории. Для квадратных матриц существует понятие
определителя.
Пусть A — квадратная матрица. Определителем (или
детерминантом) матрицы A ∈ ℝn×n назовем
число
detA = ∑α1, α2, …, αn( − 1)N(α1, α2, …, αn)⋅aα11⋅⋅⋅aαnn,
где α1, α2, …, αn — перестановка
чисел от 1 до n,
N(α1, α2, …, αn) — число инверсий в
перестановке, суммирование ведется по всем возможным перестановкам длины
n.
Не стоит расстраиваться, если это определение понятно не до конца — в
дальнейшем в таком виде оно не понадобится.
Например, для матрицы размера 2×2 получается:
det⎛⎜⎝
a11
a12
a21
a22
⎞⎟⎠ = a11a22 − a12a21
Вычисление определителя матрицы по определению требует порядка
n! операций, поэтому разработаны методы, которые позволяют
вычислять его быстро и эффективно.
В NumPy определитель матрицы вычисляется с помощью функции
numpy.linalg.det(a), где a — исходная матрица.
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=np.float32) det = np.linalg.det(a)
print ("Матрица:n", a) print ("Определитель:n", det)
Матрица: [[1. 2. 1.] [1. 1. 4.] [2. 3. 6.]] Определитель: -1.0
Рассмотрим одно интересное свойство определителя. Пусть у нас есть
параллелограмм с углами в точках
(0, 0), (c, d), (a + c, b + d), (a, b) (углы даны в порядке обхода по
часовой стрелке). Тогда площадь этого параллелограмма можно вычислить
как модуль определителя матрицы
⎛⎜⎝
a
c
b
d
⎞⎟⎠.
Похожим образом можно выразить и объем параллелепипеда через
определитель матрицы размера 3×3.
10. Ранг матрицы
Напоминание теории. Рангом матрицы A называется
максимальное число линейно независимых строк (столбцов) этой матрицы.
В NumPy ранг матрицы вычисляется с помощью функции
numpy.linalg.matrix_rank(M, tol=None), где M — матрица,
tol — параметр, отвечающий за некоторую точность вычисления. В
простом случае можно его не задавать, и функция сама определит
подходящее значение этого параметра.
a = np.array([[1, 2, 3], [1, 1, 1], [2, 2, 2]]) r = np.linalg.matrix_rank(a)
print ("Матрица:n", a) print ("Ранг матрицы:", r)
Матрица: [[1 2 3] [1 1 1] [2 2 2]] Ранг матрицы: 2
С помощью вычисления ранга матрицы можно проверять линейную
независимость системы векторов.
Допустим, у нас есть несколько векторов. Составим из них матрицу, где
наши векторы будут являться строками. Понятно, что векторы линейно
независимы тогда и только тогда, когда ранг полученной матрицы совпадает
с числом векторов. Приведем пример:
a = np.array([1, 2, 3]) b = np.array([1, 1, 1]) c = np.array([2, 3, 5]) m = np.array([a, b, c])
print (np.linalg.matrix_rank(m) == m.shape[0])
True
11. Системы линейных уравнений
Напоминание теории. Системой линейных алгебраических уравнений
называется система вида Ax = b, где
A ∈ ℝn×m, x ∈ ℝm×1, b ∈ ℝn×1.
В случае квадратной невырожденной матрицы A решение системы
единственно.
В NumPy решение такой системы можно найти с помощью функции
numpy.linalg.solve(a, b), где первый аргумент — матрица
A, второй — столбец b.
a = np.array([[3, 1], [1, 2]]) b = np.array([9, 8]) x = np.linalg.solve(a, b)
print ("Матрица A:n", a) print ("Вектор b:n", b) print ("Решение системы:n", x)
Матрица A: [[3 1] [1 2]] Вектор b: [9 8] Решение системы: [2. 3.]
Убедимся, что вектор x действительно является решением системы:
print (a.dot(x))
[9. 8.]
Бывают случаи, когда решение системы не существует. Но хотелось бы все
равно “решить” такую систему. Логичным кажется искать такой вектор
x, который минимизирует выражение
‖Ax − b‖2 — так мы приблизим выражение
Ax к b.
В NumPy такое псевдорешение можно искать с помощью функции
numpy.linalg.lstsq(a, b, …), где первые два аргумента такие
же, как и для функции numpy.linalg.solve(). Помимо решения
функция возвращает еще три значения, которые нам сейчас не понадобятся.
a = np.array([[0, 1], [1, 1], [2, 1], [3, 1]]) b = np.array([-1, 0.2, 0.9, 2.1]) x, res, r, s = np.linalg.lstsq(a, b, rcond=None)
print ("Матрица A:n", a) print ("Вектор b:n", b) print ("Псевдорешение системы:n", x)
Матрица A: [[0 1] [1 1] [2 1] [3 1]] Вектор b: [-1. 0.2 0.9 2.1] Псевдорешение системы: [ 1. -0.95]
12. Обращение матриц
Напоминание теории. Для квадратных невырожденных матриц определено
понятие обратной матрицы.
Пусть A — квадратная невырожденная матрица. Матрица
A − 1 называется обратной матрицей к A, если
AA − 1 = A − 1A = I,
где I — единичная матрица.
В NumPy обратные матрицы вычисляются с помощью функции
numpy.linalg.inv(a), где a — исходная матрица.
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=np.float32) b = np.linalg.inv(a)
print ("Матрица A:n", a) print ("Обратная матрица к A:n", b) print ("Произведение A на обратную должна быть единичной:n", a.dot(b))
Матрица A: [[1. 2. 1.] [1. 1. 4.] [2. 3. 6.]] Обратная матрица к A: [[ 6. 9. -7.] [-2. -4. 3.] [-1. -1. 1.]] Произведение A на обратную должна быть единичной: [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
13. Собственные числа и собственные вектора матрицы
Напоминание теории. Для квадратных матриц определены понятия
собственного вектора и собственного числа.
Пусть A — квадратная матрица и
A ∈ ℝn×n. Собственным вектором матрицы
A называется такой ненулевой вектор
x ∈ ℝn, что для некоторого
λ ∈ ℝ выполняется равенство
Ax = λx. При этом λ называется
собственным числом матрицы A. Собственные числа и
собственные векторы матрицы играют важную роль в теории линейной алгебры
и ее практических приложениях.
В NumPy собственные числа и собственные векторы матрицы вычисляются
с помощью функции numpy.linalg.eig(a), где a — исходная
матрица. В качестве результата эта функция выдает одномерный массив
w собственных чисел и двумерный массив v, в котором по
столбцам записаны собственные вектора, так что вектор v[:, i]
соотвествует собственному числу w[i].
a = np.array([[-1, -6], [2, 6]]) w, v = np.linalg.eig(a)
print ("Матрица A:n", a) print ("Собственные числа:n", w) print ("Собственные векторы:n", v)
Матрица A: [[-1 -6] [ 2 6]] Собственные числа: [2. 3.] Собственные векторы: [[-0.89442719 0.83205029] [ 0.4472136 -0.5547002 ]]
Обратите внимание: у вещественной матрицы собственные значения или
собственные векторы могут быть комплексными.
14. Расстояния между векторами
Вспомним некоторые нормы, которые можно ввести в пространстве
ℝn, и рассмотрим, с помощью каких библиотек и
функций их можно вычислять в NumPy.
p-норма
p-норма (норма Гёльдера) для вектора
x = (x1, …, xn) ∈ ℝn вычисляется по
формуле:
‖x‖p = (n∑i = 1|xi|p)1 ⁄ p, p ≥ 1.
В частных случаях при: * p = 1 получаем ℓ1 норму
* p = 2 получаем ℓ2 норму
Далее нам понабится модуль numpy.linalg, реализующий некоторые
приложения линейной алгебры. Для вычисления различных норм мы используем
функцию numpy.linalg.norm(x, ord=None, …), где x —
исходный вектор, ord — параметр, определяющий норму (мы
рассмотрим два варианта его значений — 1 и 2). Импортируем эту функцию:
from numpy.linalg import norm
ℓ1 норма
ℓ1 норма (также известная как манхэттенское
расстояние)
для вектора x = (x1, …, xn) ∈ ℝn
вычисляется по формуле:
‖x‖1 = n∑i = 1|xi|.
Ей в функции numpy.linalg.norm(x, ord=None, …) соответствует
параметр ord=1.
a = np.array([1, 2, -3]) print('Вектор a:', a)
Вектор a: [ 1 2 -3]
print('L1 норма вектора a:n', norm(a, ord=1))
L1 норма вектора a: 6.0
ℓ2 норма
ℓ2 норма (также известная как евклидова норма) для вектора
x = (x1, …, xn) ∈ ℝn вычисляется по
формуле:
‖x‖2 = √(n∑i = 1(xi)2).
Ей в функции numpy.linalg.norm(x, ord=None, …) соответствует
параметр ord=2.
print ('L2 норма вектора a:n', norm(a, ord=2))
L2 норма вектора a: 3.7416573867739413
Более подробно о том, какие еще нормы (в том числе матричные) можно
вычислить, см.
документацию.
15. Расстояния между векторами
Для двух векторов x = (x1, …, xn) ∈ ℝn и
y = (y1, …, yn) ∈ ℝn ℓ1 и
ℓ2 раccтояния вычисляются по следующим формулам
соответственно:
ρ1(x, y) = ‖x − y‖1 = n∑i = 1|xi − yi|
ρ2(x, y) = ‖x − y‖2 = √(n∑i = 1(xi − yi)2).
a = np.array([1, 2, -3]) b = np.array([-4, 3, 8]) print ('Вектор a:', a) print ('Вектор b:', b)
Вектор a: [ 1 2 -3] Вектор b: [-4 3 8]
print ('L1 расстояние между векторами a и b:n', norm(a - b, ord=1)) print ('L2 расстояние между векторами a и b:n', norm(a - b, ord=2))
L1 расстояние между векторами a и b: 17.0 L2 расстояние между векторами a и b: 12.12435565298214
16. Скалярное произведение и угол между векторами
a = np.array([0, 5, -1]) b = np.array([-4, 9, 3]) print ('Вектор a:', a) print ('Вектор b:', b)
Вектор a: [ 0 5 -1] Вектор b: [-4 9 3]
Скалярное произведение в пространстве ℝn для двух
векторов x = (x1, …, xn) и
y = (y1, …, yn) определяется как:
⟨x, y⟩ = n∑i = 1xiyi.
Длиной вектора x = (x1, …, xn) ∈ ℝn
называется квадратный корень из скалярного произведения, то есть длина
равна евклидовой норме вектора:
|x| = √(⟨x, x⟩) = √(n∑i = 1x2i) = ‖x‖2.
Теперь, когда мы знаем расстояние между двумя ненулевыми векторами и их
длины, мы можем вычислить угол между ними через скалярное произведение:
⟨x, y⟩ = |x||y|cos(α) ⟹ cos(α) = (⟨x, y⟩)/(|x||y|),
где α ∈ [0, π] — угол между векторами x и
y.
cos_angle = np.dot(a, b) / norm(a) / norm(b) print ('Косинус угла между a и b:', cos_angle) print ('Сам угол:', np.arccos(cos_angle))
Косинус угла между a и b: 0.8000362836474323 Сам угол: 0.6434406336093618
17. Комплексные числа в питоне
Напоминание теории. Комплексными числами называются числа вида
x + iy, где x и y — вещественные числа, а
i — мнимая единица (величина, для которой выполняется равенство
i2 = − 1). Множество всех комплексных чисел обозначается
буквой ℂ (подробнее про комплексные числа см.
википедию).
В питоне комплескные числа можно задать следующим образом (j
обозначает мнимую единицу):
a = 3 + 2j b = 1j
print ("Комплексное число a:n", a) print ("Комплексное число b:n", b)
Комплексное число a: (3+2j) Комплексное число b: 1j
С комплексными числами в питоне можно производить базовые арифметические
операции так же, как и с вещественными числами:
c = a * a d = a / (4 - 5j)
print ("Комплексное число c:n", c) print ("Комплексное число d:n", d)
Комплексное число c: (5+12j) Комплексное число d: (0.0487804878048781+0.5609756097560976j)
Задания: (Блок 2)
Задание 3:
Рассмотрим сложную математическую функцию на отрезке [1, 15]:
f(x) = sin(x / 5) * exp(x / 10) + 5 * exp(-x / 2)
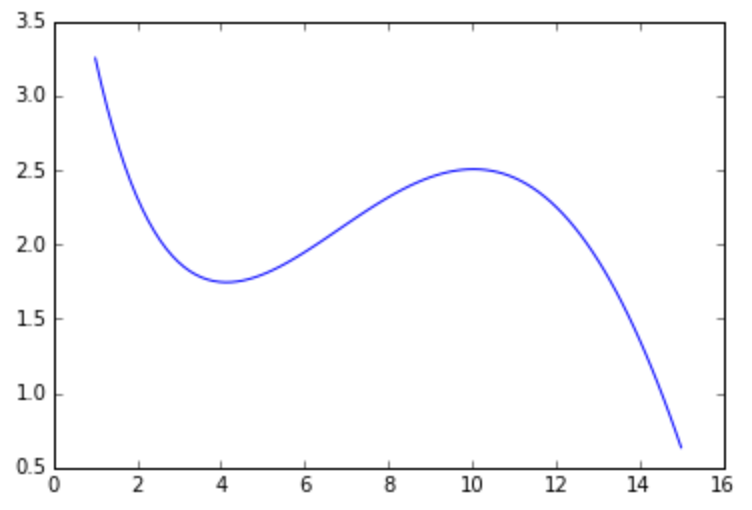
Она может описывать, например, зависимость оценок, которые выставляют
определенному сорту вина эксперты, в зависимости от возраста этого вина.
Мы хотим приблизить сложную зависимость с помощью функции из
определенного семейства. В этом задании мы будем приближать указанную
функцию с помощью многочленов.
Как известно, многочлен степени n (то есть w0 +
w1x + w2x2 + … + wnxn)
однозначно определяется любыми n + 1 различными точками, через которые
он проходит. Это значит, что его коэффициенты w0, … wn
можно определить из следующей системы линейных уравнений:
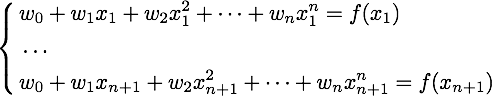
где через x1, …, xn, xn + 1 обозначены точки, через которые
проходит многочлен, а через f(x1), …, f(xn), f(xn + 1) —
значения, которые он должен принимать в этих точках.
Воспользуемся описанным свойством, и будем находить приближение функции
многочленом, решая систему линейных уравнений.
- Сформируйте систему линейных уравнений (то есть задайте матрицу
коэффициентов A и свободный вектор b) для многочлена первой степени,
который должен совпадать с функцией f в точках 1 и 15. Решите данную
систему с помощью функции scipy.linalg.solve. Нарисуйте функцию f и
полученный многочлен. Хорошо ли он приближает исходную функцию? - Повторите те же шаги для многочлена второй степени, который совпадает
с функцией f в точках 1, 8 и 15. Улучшилось ли качество
аппроксимации? - Повторите те же шаги для многочлена третьей степени, который
совпадает с функцией f в точках 1, 4, 10 и 15. Хорошо ли он
аппроксимирует функцию? Коэффициенты данного многочлена (четыре числа
в следующем порядке: w_0, w_1, w_2, w_3) являются ответом на задачу.
Округлять коэффициенты не обязательно, но при желании можете
произвести округление до второго знака (т.е. до числа вида 0.42)
- Get Length of a NumPy Array With the
numpy.sizeProperty in Python - Get Length of a NumPy Array With the
numpy.shapeFunction in Python

This tutorial will discuss the methods to get the length of a NumPy array.
Get Length of a NumPy Array With the numpy.size Property in Python
The numpy.size property gets the total number of elements in a NumPy array. We can use this property to accurately find the number of elements in a NumPy array in Python. See the following code example.
import numpy as np
array = np.array([1,2,3,4,5,6,7,8,9])
print(array.size)
Output:
In the above code, we get the number of elements in the array array with the numpy.size property in Python. This method works great with one-dimensional arrays. It does not consider the multi-dimensional arrays; it only gives us the total number of elements in an array. It is shown in the code example below.
import numpy as np
array = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(array.size)
Output:
In the above code, we get the number of elements in the multi-dimensional array array with the numpy.size property in Python. It also gives us the value 9 because the total number of elements is the same as in the previous example. This is the reason why this method is not suitable for multi-dimensional arrays.
Get Length of a NumPy Array With the numpy.shape Function in Python
If we also want to know the number of elements in each dimension of the NumPy array, we have to use the numpy.shape function in Python. The numpy.shape function returns a tuple in the form of (x, y), where x is the number of rows in the array and y is the number of columns in the array. We can find the total number of elements in the array like we have done in the previous section by multiplying both x and y with each other. See the following code example.
import numpy as np
array = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(array.shape)
Output:
In the above code, we get the length of the multi-dimensional array array with the numpy.shape function in Python. We can now find the total number of elements by multiplying the values in the tuple with each other. This method is preferred over the previous method because it gives us the number of rows and columns.
