Как найти длину вектора в прямоугольнике диагонали

Длина вектора — основные формулы

Время чтения: 16 минут

Основные понятия вектора

Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.

Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».

Вектор — это отрезок с определённой длиной и направлением.

Графическое изображение вектора – отрезок который имеет указание направления в виде стрелки.

Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.

Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.

• Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
• Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.

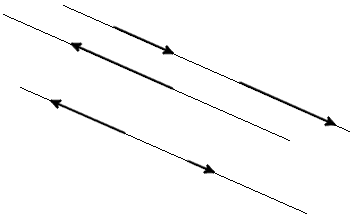
• Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
• Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
• Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
  Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

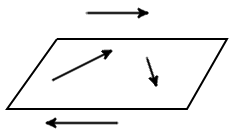
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.

Как найти длину вектора

Модуль вектора а будем обозначать .

Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.

На взятой системе координат, от её начала отложим вектор
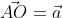В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.

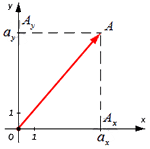
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует

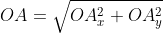
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 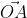получаем

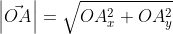
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор дан в формате разложения по координатным векторам 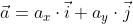, то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.

Чтобы рассчитать длину = (3, √x), расположенного в прямоугольной системе координат.

Чтобы найти модуль вектора используем ранее приведённую формулу

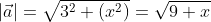
Ответ: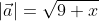

Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор =(aₓ ; aᵧ ; a )

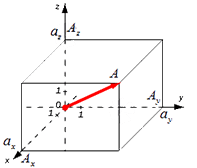
В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО – диагональ прямоугольного параллелепипеда), поэтому

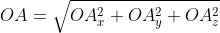
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:

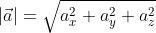
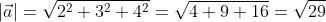
Ответ: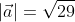

Длина вектора через координаты точек начала и конца

Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.

Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле

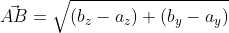
При этом формула вычисления длины вектора для трёхмерного пространства, с координатам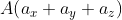и и 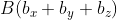), будет следующей:

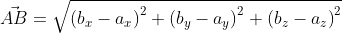
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)

Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:

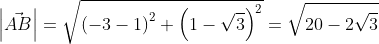
Существует второй вариант решения, где формулы применяются по очереди:

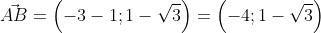
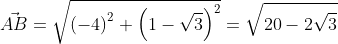
Ответ: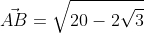

Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))

В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )

Длина вектора по теореме косинусов

Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.

К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.

Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).

В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)

Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.

длина вектора формула для трёхмерного пространства;

длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.

Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.

В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.

Применение векторов в других сферах

Понятие и вычисление вектора важно не только в математике, но и других науках:

• в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
• в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
• в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
• географии. Вектором обозначается движение воздушных масс, или течение реки;

Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.

Нахождение длины вектора, примеры и решения

Длина вектора – основные формулы

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

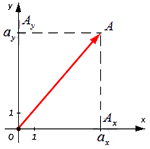
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e

Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

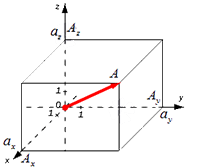
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Вычислить длину вектора a → = 4 · i → – 3 · j → + 5 · k → , где i → , j → , k → – орты прямоугольной системы координат.

Дано разложение вектора a → = 4 · i → – 3 · j → + 5 · k → , его координаты равны a → = 4 , – 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( – 3 ) 2 + 5 2 = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x – a x ; b y – a y ) значит, его длина может быть определена по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2

А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B – 3 , 1 .

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x – a x ) 2 + ( b y – a y ) 2 : A B → = ( – 3 – 1 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( – 3 – 1 ; 1 – 3 ) = ( – 4 ; 1 – 3 ) ; A B → = ( – 4 ) 2 + ( 1 – 3 ) 2 = 20 – 2 3 . –

Ответ: A B → = 20 – 2 3 .

Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .

Для начала распишем длину вектора A B → по формуле: A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 = ( 5 – 0 ) 2 + ( 2 – 1 ) 2 + ( λ 2 – 2 ) 2 = 26 + ( λ 2 – 2 ) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :

26 + ( λ 2 – 2 ) 2 = 30 26 + ( λ 2 – 2 ) 2 = 30 ( λ 2 – 2 ) 2 = 4 λ 2 – 2 = 2 и л и λ 2 – 2 = – 2 λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = – 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 – 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 – 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x – a x ) 2 + ( b y – a y ) 2 или A B → = ( b x – a x ) 2 + ( b y – a y ) 2 + ( b z – a z ) 2 , в некоторых случаях следует использовать теорему косинусов.

Онлайн калькулятор. Модуль вектора. Длина вектора

Этот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал.

Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам

Размерность вектора:

Форма представления вектора:

Инструкция использования калькулятора для вычисления длины вектора

Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел..

Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Вычисления длины вектора (модуля вектора)

Например, для вектора a = x; a_y; a_z> длина вектора вычисляется cледующим образом:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/dlina_vectora/

http://ru.onlinemschool.com/math/assistance/vector/length/

[/spoiler]

Длина вектора – основные формулы

Длину вектора a→ будем обозначать a→. Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат Oxy. Пусть в ней задан некоторый вектор a→ с координатами ax;ay. Введем формулу для нахождения длины (модуля) вектора a→ через координаты ax и ay.

От начала координат отложим вектор OA→=a→. Определим соответственные проекции точки A на координатные оси как Ax и Ay . Теперь рассмотрим прямоугольник OAxAAy с диагональю OA.

Из теоремы Пифагора следует равенство OA2=OAx2+OAy2, откуда OA=OAx2+OAy2. Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что OAx2=ax2 и OAy2=ay2, а по построению длина OA равна длине вектора OA→, значит, OA→=OAx2+OAy2.

Отсюда получается, что формула для нахождения длины вектора a→=ax;ay имеет соответствующий вид: a→=ax2+ay2.

Если вектор a→ дан в виде разложения по координатным векторам a→=ax·i→+ay·j→, то вычислить его длину можно по той же формуле a→=ax2+ay2, в данном случае коэффициенты ax и ay выступают в роли координат вектора a→ в заданной системе координат.

Формула для нахождения длины вектора a→=ax;ay;az по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае OA2=OAx2+OAy2+OAz2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда OA=OAx2+OAy2+OAz2. Из определения координат вектора можем записать следующие равенства OAx=ax; OAy=ay; OAz=az; , а длина ОА равна длине вектора, которую мы ищем, следовательно, OA→=OAx2+OAy2+OAz2.

Отсюда следует, что длина вектора a→=ax;ay;az равна a→=ax2+ay2+az2.

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A(ax;ay) и B(bx;by), отсюда вектор AB→ имеет координаты (bx-ax; by-ay)значит, его длина может быть определена по формуле: AB→=(bx-ax)2+(by-ay)2

А если даны точки с заданными координатами A(ax;ay;az) и B(bx;by;bz) в трехмерном пространстве, то длину вектора AB→ можно вычислить по формуле

AB→=(bx-ax)2+(by-ay)2+(bz-az)2

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов AB→, AC→ и угол между ними (или косинус угла), а требуется найти длину вектора BC→ или CB→. В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ABC, вычислить длину стороны BC, которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Итак, для нахождения длины вектора по координатам существуют следующие формулы a→=ax2+ay2 или a→=ax2+ay2+az2, по координатам точек начала и конца вектора AB→=(bx-ax)2+(by-ay)2 или AB→=(bx-ax)2+(by-ay)2+(bz-az)2, в некоторых случаях следует использовать теорему косинусов.

Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор,  как находить его длину, и как умножать вектор на число,  а также как находить сумму, разность и скалярное произведение двух векторов.

Как обычно, немного самой необходимой теории.

Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:

Здесь точка А – начало вектора, а точка В – его конец.

У вектора есть два параметра: его длина и направление.

Длина вектора – это длина отрезка, соединяющего начало и конец вектора. Длина вектора  обозначается 

Два вектора называются равными, если они имеют одинаковую длину и сонаправлены.

Два вектора называются сонаправленными, если они лежат на параллельных прямых и направлены в одну сторону: вектора и   сонаправлены:

Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора  и , а также  и  направлены в противоположные стороны:

Вектора, лежащие на параллельных прямых называются коллинеарными: вектора ,  и  – коллинеарны.

Произведением вектора  на число  называется вектор, сонаправленный вектору , если  , и направленный в противоположную сторону, если  , и длина которого равна длине вектора  , умноженной на :

=k:

Чтобы сложить  два вектора  и , нужно начало вектора   соединить с концом вектора . Вектор суммы соединяет начало вектора  с концом вектора :

Это правило сложения векторов называется правилом треугольника.

Чтобы сложить два вектора по правилу параллелограмма, нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку  начала векторов с противоположным углом параллелограмма:

Разность двух векторов определяется через сумму: разностью векторов  и называется такой вектор , который в сумме с вектором  даст вектор :

:        

Отсюда вытекает правило нахождения разности двух векторов: чтобы из вектора   вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора  с концом вектора ( то есть конец вычитаемого с концом уменьшаемого):

Чтобы найти угол между вектором  и вектором , нужно отложить эти вектора от одной точки. Угол, образованный лучами, на которых лежат вектора, называется углом между векторами: 

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

Предлагаю вам решить задачи  из Открытого банка заданий для  подготовки к ЕГЭ  по математике, а затем сверить све решение с ВИДЕОУРОКАМИ:

1. Задание 4 (№ 27709)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов   и .

2. Задание 4 (№ 27710)

Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов   и .  (чертеж из предыдущей задачи).

3. Задание 4 (№ 27711)

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов   и .

4. Задание 4 (№ 27712)

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину разности векторов   и . (чертеж из предыдущей задачи).

5. Задание 4 (№ 27713)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .

6. Задание 4 (№ 27714)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  + .

7.Задание 4 (№ 27715)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора – .(чертеж из предыдущей задачи).

8.Задание 4 (№ 27716)

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора – .

9. Задание 4 (№ 27717)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  + .

10. Задание 4 (№ 27718)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  – .(чертеж из предыдущей задачи).

11.Задание 4 (№ 27719)

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов   и .(чертеж из предыдущей задачи).

12. Задание 4 (№ 27720)

Стороны правильного треугольника ABC равны   Найдите длину вектора   +.

13. Задание 4 (№ 27721)

Стороны правильного треугольника ABC равны 3. Найдите длину вектора  –.(чертеж из предыдущей задачи).

14. Задание 4 (№ 27722)

Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов  и . (чертеж из предыдущей задачи).

И.В. Фельдман, репетитор по математике.

как доказать, какие нужны условия, примеры задач для 9 класса

Что такое равенство двух векторов в геометрии 

Основными характеристиками вектора в пространстве и на плоскости являются его длина и направление, и именно на этом основано определение равенства векторов.

Для начала введем понятие коллинеарности.

Определение 1

Коллинеарность — характеристика взаиморасположения ненулевых векторов. Векторы коллинеарны, если расположены на одной прямой или параллельных прямых. Коллинеарные векторы допустимо называть параллельными.

Из определения нулевого вектора (вектор, у которого начальная и конечная точки совпадают, и длина равна нулю) ясно, что нулевой вектор коллинеарен любому другому вектору.

Если направления коллинеарных векторов совпадают, то их называют сонаправленными и обозначают b→↑↑d→, если нет — противоположно направленными и обозначают b→↑↓d→.

Определение 2

Равными считают те векторы, длины которых равны, а направления совпадают.

Понятие, признаки, какие нужны условия

Понятие равенства векторов применяется не только в геометрии, но и в алгебре, и особенно часто в физике, где действующие на тела сила представляют в векторном виде.

Необходимые признаки следуют из определения равных векторов. Итак, векторы равны, если:

• их модули или координаты равны;
• они сонаправлены.

Остановимся подробнее на первом признаке. Модуль — длина вектора обозначается как left|overrightarrow bright|. Формула для вычисления длины вектора на плоскости имеет вид:

Формула 

b→=x2+y2

Под корнем находится сумма координат вектора, то есть векторы равны, если доказано либо равенство их модулей, либо координат.

Необходимым условием равенства векторов является сочетание двух признаков: векторы должны быть сонаправлены, а их длины равными.

Отметим, что наличие только одного из признаков не делает векторы равными. Так, противоположно направленные векторы с одинаковыми длинами не равны. Сонаправленные векторы с отличными по величине модулями также нельзя назвать равными.

Доказательство теоремы, формулы

Теорема 

Равные векторы обладают следующими свойствами:

1. Вектор равен самому себе.
2. Для равных векторов справедливо тождество: b→=d→⇔d→=b→.
3. Если векторы равны третьему, то они равны друг другу.

 Доказательство. Первые два свойства прямо следуют из определения равенства векторов. Докажем третье свойство. Для этого воспользуемся правилом параллельного переноса. Пусть имеются три вектора, при этом b→=d→ и f→=d→. Начальную и конечную граничные точки f→ совместим с соответствующими граничными точками d→. Так как f→=d→, векторы совпадут. По условию b→=d→, а если f→ и d→ совпали, то b→=f→. Теорема доказана.

Кратко остановимся на используемых для решения задач формулы математических операций с векторами:

1. Умножение b→ на число k: d→=k·b→.
2. Сложение и вычитание векторов производят по методу треугольника.

Примеры задач для 9 класса

Задача 1

Дано: d→=b→. Известны координаты вектора b→ (2; 21) и одна координата вектора d→ (3; y). Найти координату y d→.

Решение

По условию задачи векторы равны, а значит, равных их модули. Составим уравнение с неизвестной переменной — y.

22+(21)2=32+y2

Откуда: 25=9+y2⇒y=4.

Ответ: d→ (3; 4).

Задача 2

Дано: два вектора MN→ и KL→ такие, что MN=KL. По точкам M и L построен отрезок ML, по точкам N и K — NK. Доказать, что середины ML и NK совпадают.

Решение.

Сделаем рисунок по условию задачи.

Видно, что MNLK — параллелограмм. Тогда ML и NK являются диагоналями MNLK. По свойству параллелограмма, точка пересечения диагоналей делит их пополам. То есть середина ML совпадет с серединой NK, что и требовалось доказать.

Задача 3

Дано: прямоугольник KLMN. Известны длины сторон: KL=6; LM=8. На отрезке KL обозначена точка O, при этом KO=OL. Найти длину NO→.

Решение

Прямоугольник — частный случай параллелограмма, то есть его противоположные стороны равны. Длину NO→ найдем как гипотенузу прямоугольного треугольника NKO.

NO→=KO2+NK2=KL22+LM2=9+64=73

Ответ: NO→=73.

Задача 4

Определить форму фигуры, заданной точками H, D, F, G, если имеется свободно расположенная на плоскости точка O такая, что OF→-OD→=OG→-OH→.

Решение.

Для решения задачи необходимо последовательно выполнить чертеж по известным условиям. Обозначим точку О, теперь проведем из точки OF→ и OD→. По методу треугольника построим вектор DF→, равный разности OF→ и OD→. Затем из точки О также проведем векторы OH→, OG→ и результирующий HG→. Получили четырехугольник. HDFG. По условию противоположные стороны DF и HG равны, значит, HDFG — параллелограмм.

Ответ: параллелограмм.

Векторы – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Вопросы

1. Найдите вектор (vec{a}), перпендикулярный вектору (vec{b} (5; 3)), если их длины равны.

2. Найдите вектор (vec{a}), перпендикулярный вектору (vec{b} (5; 3)), если их длины равны.

3. Определите координаты единичного вектора, сонаправленного с вектором (vec{p}(-sqrt3;1)).

4. Найдите сумму ветров (vec{a}) {1; – 2} и (vec{в}) {2; – 2}. Найдите длину вектора суммы (vec{c})

5. В равнобедренной трапеции АВСD укажите пары коллинеарных векторов.

6. Найдите скалярное произведение векторов (vec{c})  и (vec{d}), если известно, что (midvec{c}mid) = 5, (midvec{d}mid) = 8, а угол между ними равен 60°

7. Даны векторы (vec{a}) {3; 4} и (vec{в}) {– 3; 3}. Найдите угол между ними, если скалярное произведение равно 7,5(sqrt6).

8. Вычислите скалярное произведение векторов, если (vec{a}) {– 4; – 3}, (vec{в}) {1; 0}, а угол между ними равен 30°.

9. Даны векторы (vec{a}) {1; 6} и (vec{в}) {– 5; 7}. Найдите координаты вектора (vec{с}=2vec{а}+vec{в}).

10. Даны точки А(2;–1), С(3;4). Найдите абсолютную величину вектора АС.

11. (midvec{a}mid)= 1, (midvec{в}mid)= 6, a cos(alpha) = (frac 13). Найдите скалярное произведение данных векторов.

12. Найдите значение m, при котором векторы (vec{a}) и (vec{в}) перпендикулярны, если (vec{a}) {m; – 8} и (vec{в}) {4; 3}

13. Даны точки А (3;8), В (–7;5), С (k; 11). Найдите значение k, при котором (vec{BA}) (bot)(vec{CB}).

14. Найдите координаты вектора (vec{c}=vec{a}-3vec{b}), если (vec{a}) {3; 2}, (vec{b}) {– 3; 1}

15. Вычислите скалярное произведение векторов, если (midvec{a}mid) = 2, (midvec{b}mid) = 3 и угол между ними равен 135°

16. Дан треугольник ABC. Выразите через векторы (vec{a}) = (vec{AB})  и (vec{b}) = (vec{AC}) вектор (vec{CB})

17. Найдите угол между векторами (vec{a}) (2; 0) и (vec{b}) (– 2 ; 2)

18. Даны векторы (vec{a}) (2; 3), (vec{b}) (–1; 0). Найдите сумму векторов (vec{a}) и (vec{b})

19. Материальная точка переместилась на 3 метра под воздействием постоянной силы в 5 ньютонов, направленной под углом 45 градусов по отношению к оси перемещения. Найдите работу этой силы.

20. Найдите скалярное произведение векторов  (vec{a}(-1;3), vec{b}(-7;5).)

21. Сколько разных векторов определяют стороны параллелограмма?

22. (vec{|a|}=7, vec{|b|}=6,) а угол между векторами   (vec a) и (vec b)  равен 120°. Найдите скалярное произведение (vec acdot (vec a+vec b).)
     

23. Даны векторы (vec a(3;4), vec b(k;2). ) При каком значении (k) эти векторы взаимно перпендикулярны?
     

24.  

    В прямоугольном треугольнике ABC C = 90°,сторона AC равна 6 см, сторона BC равна 8 см. Найдите AC+BC.

25. При каких значениях числа х векторы ( vec a(x; 3) и vec b(2; 7)) коллинеарны?

26. Даны векторы  (vec a{1;6 }), (vec b{5;7 }). Найдите скалярное произведение векторов

27. Диагонали ромба (ABCD ) равны 10 и 14. Найдите длину вектора  (vec{AB}-vec {AD}) .

28. Даны векторы (vec{а}) {2; 1,5} и (vec{в}) {3; – 1}, (vec{с}) {4,4; 3,3}.

    Найдите пары коллинеарных векторов.

29. Даны (vec{a})( – 1; 2), (vec{b})(0; 5). Найдите (vec{c} = 2vec{a} – vec{b}).

30. Даны (vec{а})( – 4; 3), (vec{в})(0; 1). Найдите скалярное произведение данных векторов.

31. Найдите значение k, при котором векторы (vecа) (– 2; 1) и (vecв) (9; k) перпендикулярны.

32. Даны (vecа)(1; 4) и (vecв)(– 3; 2). Найдите значение k, при котором вектор (vecа+vec{kв}) перпендикулярен (vecа).

33. Даны векторы (vec{а}) {3; 2}, (vec{в}){2; – 1}, (vec{c}) {7; 3}, (vec{d}) {4; – 2}. circ).

34. Даны точки А(3; 8), В( – 7; 5), С(n; 11). Найдите значение n, при котором векторы АВ и АС перпендикулярны.

35. Даны (vec{a})(– 3; 2) и (vec{c})(1; 4). Найдите значение k, при котором вектор (vec{a} + vec{kc})  перпендикулярен (vec{c}).

36. Найдите скалярное произведение векторов (vec{a}) (– 7; 3)и (vec b)(– 1; 5).

37. Сколько пар равных векторов определяют вершины квадрата?

38. (mid vec{a}mid=7; midvec{b}mid=6), угол между векторами равен 60°. Найдите скалярное произведение (vec{a}cdot(vec{a}+vec{b})).

39. Даны векторы (vec a)(1; 0), (vec b)(1; 1). При каком значении(lambda ) вектор (vec{a}+λvec{b}) перпендикулярен вектору (vec{b})?

40. В треугольнике FGH точки M и N – середины сторон FG и GH соответственно. Выразите вектор (vec{MH}) через векторы (vec{m}=vec{GM}, vec{n}=vec{GN}).

41. При каких значениях числа х векторы (vec a)(7; 3), (vec b)(x; 2) являются коллинеарными?

42. Вычислите скалярное произведение векторов, если (midvec{a}mid=4,5, midvec{b}mid=6), а угол между ними равен 60°.

43. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину суммы векторов (vec{AO}) и (vec{DO}).

44. Угол между векторами (vec a) (2; 4) и (vec b) (3; 1) равен

45. Найдите сумму векторов (vec{AB}-vec{FH}+vec{EH}-vec{CB}+vec{CE}).

46. Найдите угол между векторами (vec a) ( – 1; 2) и  (vec b) (3; – 1).

47. При каких значениях x векторы (vec a) (x; 3) и  (vec b) (2; 7) ортогональны (перпендикулярны)?

48. Даны векторы (vec{a}) {2; – 1}, (vec{b}) {– 3; 7}.  Найдите их скалярное произведение.

49. Угол между векторами (vec a) (1,2; 1,8), (vec{b}) (0,2; 0,3)

50. Сторона равностороннего треугольника KLM равна a. Найдите (|vec{KL}+vec{KM}|).

51. Укажите правильное разложение вектора (vec d) (– 4; 2) по координатным векторам (vec i) и  (vec j).

52. Дан треугольник с вершинами в точках A (1; 1), B (– 4; 3), C (2; 2).Найдите длину медианы АК.

53. Найдите координаты вектора (vec{PQ}), если P (1; – 3) и Q (3; – 1).

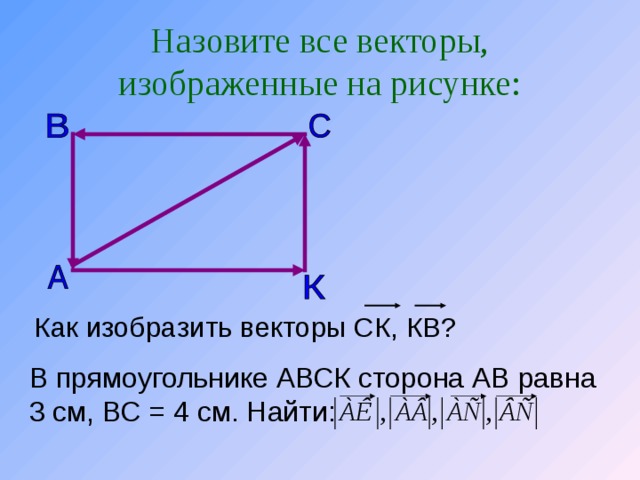
54. При каких значениях числа х векторы (vec a) (7; 3), (vec b)(x; 2) ортогональны (перпендикулярны)?

55. Вычислите скалярное произведение векторов, если (midvec{a}mid=2,5,midvec{b}mid=7), a угол между ними равен 30°.

56. Найдите длину разности векторов (vec{AO}) и (vec{DO}), если в прямоугольнике ABCD стороны AB и AD равны 3 и 4 см соответственно, а диагонали пересекаются в точке О

Сообщить об ошибке

Видео-вопрос: Использование векторов для определения площади прямоугольника по его вершинам

Прямоугольник 𝐴𝐵𝐶𝐷 имеет вершины 𝐴(−6, −7), 𝐵(0, 2), 𝐶(6, −2) и 𝐷(0, − 11).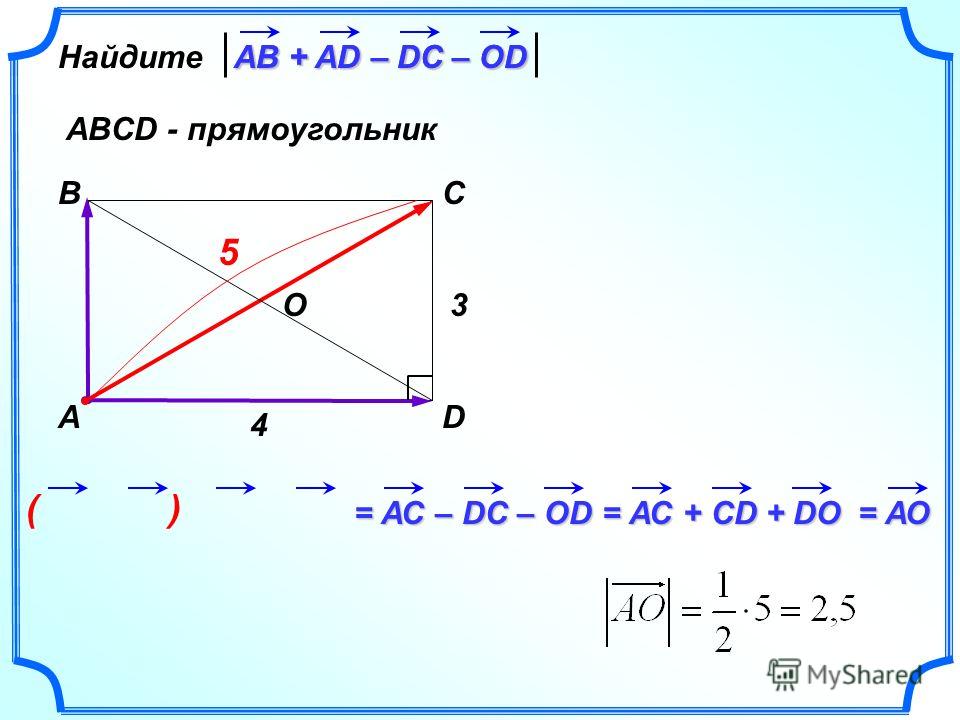 Используйте векторы, чтобы определить его площадь.

Стенограмма видео

Прямоугольник 𝐴𝐵𝐶𝐷 имеет вершины 𝐴 минус шесть, минус семь; 𝐵 ноль, два; 𝐶 шесть, минус два; и 𝐷 ноль, отрицательный 11. Используйте векторы, чтобы определить его площадь.

Начнем с рисования прямоугольника на координатной сетке. Точка 𝐴 имеет координаты минус шесть, минус семь. Точка 𝐵 имеет координаты ноль, два. Точка 𝐶 равна шести, минус два. И, наконец, точка 𝐷 имеет координаты ноль, минус 11. Нас просят вычислить площадь прямоугольника с помощью векторов. Мы знаем, что площадь любого параллелограмма равна величине векторного произведения векторов 𝐚 и 𝐛, где вектор 𝐚 и вектор 𝐛 — стороны параллелограмма. Величина векторного произведения любых двух векторов равна величине вектора 𝐚, умноженной на величину вектора 𝐛, умноженной на величину греха 𝜃, где 𝜃 — угол между двумя векторами.

Мы знаем, что прямоугольник — это особый вид параллелограмма, в котором четыре угла равны 90 градусам. Таким образом, площадь прямоугольника 𝐴𝐵𝐶𝐷 равна величине векторного произведения вектора 𝚨𝚩 и вектора 𝚨𝐃. Это, в свою очередь, равно величине вектора 𝚨𝚩, умноженной на величину вектора 𝚨𝐃, умноженной на величину греха 𝜃. 𝜃 равно 90 градусам, а мы знаем, что грех 90 градусов равен единице. Таким образом, площадь прямоугольника равна величине вектора 𝚨𝚩, умноженной на величину вектора 𝚨𝐃. Теперь мы освободим место, чтобы мы могли вычислить эти два значения.

Компоненты вектора 𝚨𝚩 будут равны нулю минус минус шесть и два минус минус семь. Ноль минус минус шесть равно шести, а два минус минус семь равно девяти. Следовательно, вектор 𝚨𝚩 равен шести, девяти. Мы можем найти величину любого вектора, найдя сумму квадратов каждого из компонентов, а затем извлекая из ответа квадратный корень. Шесть в квадрате равно 36, а девять в квадрате равно 81. Следовательно, величина вектора 𝚨𝚩 равна квадратному корню из 117. Это упрощает до корня из трех 13.

Теперь мы можем повторить этот процесс для вектора 𝚨𝐃.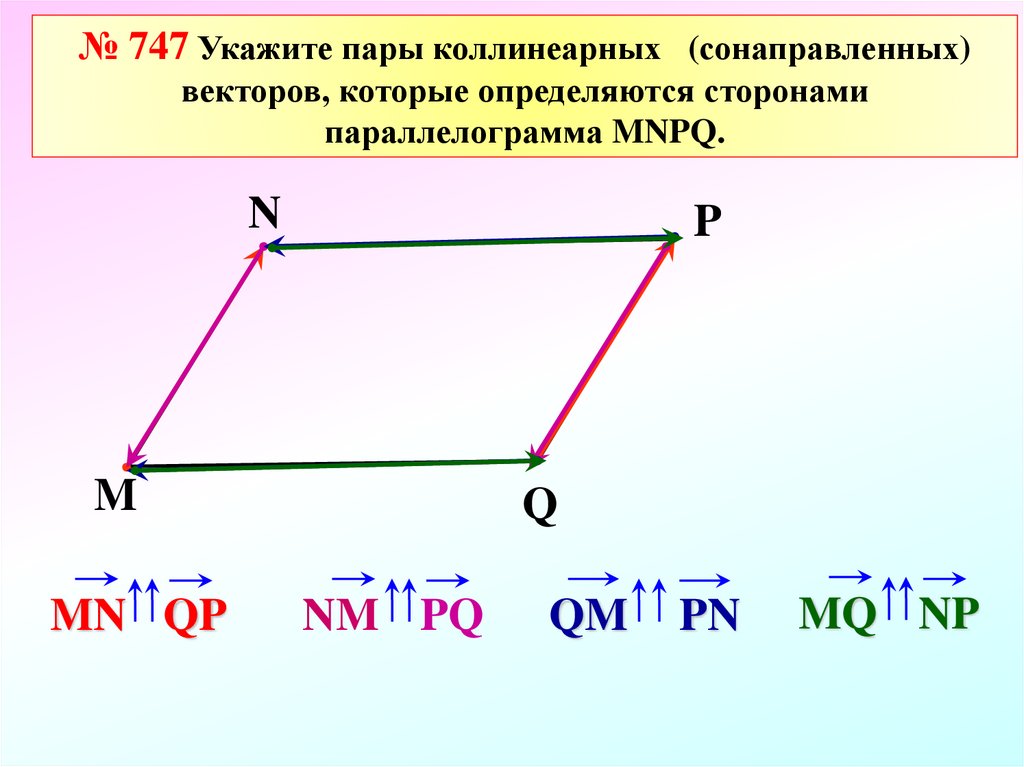 Это будет иметь 𝑥-компоненту, равную нулю минус минус шесть, и 𝑦-компоненту, равную минус 11 минус минус семь. Это равно шести, минус четыре. Таким образом, величина вектора 𝚨𝐃 равна квадратному корню из шести в квадрате плюс минус четыре в квадрате. Поскольку шесть в квадрате равно 36, а минус четыре в квадрате равен 16, у нас остается квадратный корень из 52. Это упрощается до двух корней из 13. Подстановка этих значений в наше уравнение дает нам три корня из 13, умноженные на два корня из 13. Три, умноженное на два, равно шести, а корень 13, умноженный на корень 13, равен 13. Это дает нам шесть, умноженное на 13, что равно 78. Площадь прямоугольника 𝐴𝐵𝐶𝐷 составляет 78 единиц площади.

Как найти длину прямоугольника, периметр и ширина которого заданы?

Измерение влечет за собой процессы измерения и всех расчетов, относящихся к различным геометрическим формам, происходящие в математической теории, а также в нашей повседневной жизни. Изучение всех геометрических фигур подпадает под сферу измерения. Геометрические формы, такие как треугольники, прямоугольники, четырехугольники, круг и т. д. Здесь прямоугольник обсуждается ниже,

Прямоугольник

Прямоугольник определяется как тип четырехугольника, противоположные стороны которого всегда параллельны и равны по длине. Соседние стороны пересекаются друг с другом под прямым углом. Как и у всех других четырехугольников, сумма всех четырех углов прямоугольника также равна 360°. Прямоугольник — это двумерная фигура, которая имеет только две пропорции длины и ширины, представленные каждой парой четырех сторон.

На приведенном выше рисунке изображен прямоугольник ABDC, где сторона AB параллельна стороне CD, а сторона AC параллельна стороне BD. Здесь AB и CD обозначают длину прямоугольника, а AC и BD — ширину. Сумма всех четырех прямых углов равна 360°.

Периметр прямоугольника

Периметр двумерной геометрической фигуры представляет собой сумму длин всех его сторон. Итак, периметр прямоугольника ABDC будет равен:

AB + AC + CD + BD

= l + b + l + b

= 2l + 2b

= 2(l + b).

Следовательно, периметр прямоугольника в два раза больше суммы его длины и ширины.

Как найти длину прямоугольника, периметр и ширина которого заданы?

Решение:

Пусть данный периметр равен P единицам, а ширина равна x единицам. Пусть длина обозначается l.

Поскольку Периметр прямоугольника = 2(l + b)

⇒ P = 2l + 2b

⇒ 2l = P – 2b

⇒ l =

Приведенную выше формулу можно использовать для нахождения длины прямоугольника, периметр и ширина которого заданы.

Аналогичные задачи

Вопрос 1: Найдите длину прямоугольника, периметр которого равен 50 см, а ширина 10 см.

Решение:

P = 2 (L + B)

Дано: P = 50 см и B = 10 см

⇒ L =

⇒ L =

⇒ L = 30/2

⇒ l = 15 см

Вопрос 2: Найдите длину прямоугольника, периметр которого равен 60 см, а ширина 5 см.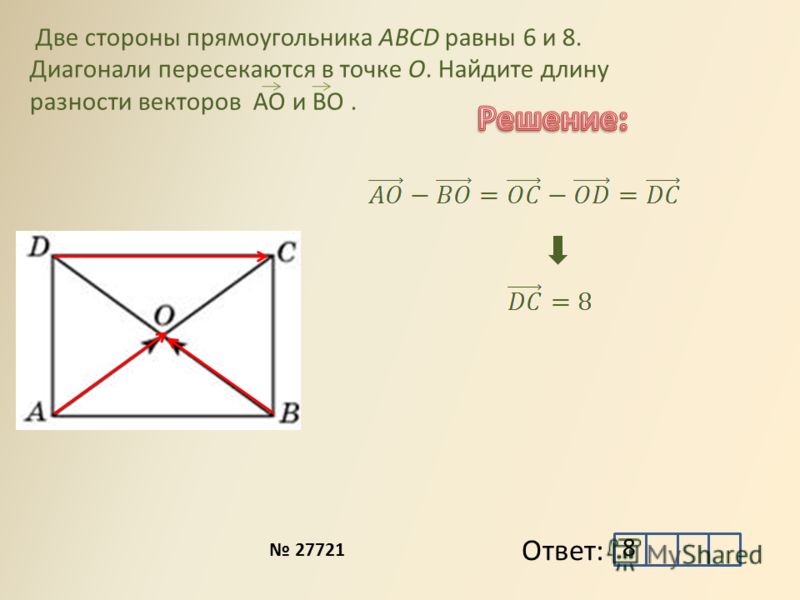

Решение:

P = 2 (L + B)

Дано: P = 60 см и B = 5 см

⇒ L =

⇒ L =

⇒ L = 50/2

⇒ l = 25 см

Вопрос 3: Найдите длину прямоугольника, периметр которого равен 60 см, а ширина 20 см.

Решение:

P = 2(l + b)

Дано: P = 60 см и b = 20 см

Вопрос 4: Найдите длину прямоугольника, периметр которого равен 80 см, а ширина 10 см.

Решение:

P = 2 (L + B)

Дано: P = 80 см и B = 10 см

⇒ L =

⇒ L =

⇒ L = 60/2

⇒ l = 30 см

Вопрос 5: Найдите длину прямоугольника, периметр которого равен 100 см, а ширина 10 см.

Решение:

P = 2 (L + B)

Дано: P = 100 см и B = 10 см

⇒ L =

⇒ L =

⇒ L = 80/2

⇒ l = 40 см

Вопрос 6: Найдите длину прямоугольника, периметр которого равен 60 см, а ширина 10 см.

    Сумма векторов. Длина вектора. Дорогие друзья, в составе типов задний экзамена присутствует группа задач с векторами. Задания довольно широкого спектра (важно знать теоретические основы). Большинство решается устно. Вопросы связаны с нахождением длины вектора, суммы (разности) векторов, скалярного произведения. Так же много заданий, при решении которых необходимо осуществить действия с координатами векторов.

Теория касающаяся темы векторов несложная, и её необходимо хорошо усвоить. В этой статье разберём задачи связанные с нахождением длины вектора, также суммы (разности) векторов. Некоторые теоретические моменты:

Понятие вектора

Вектор — это направленный отрезок.

Все векторы, имеющие одинаковое направление и равные по длине являются равными.

*Все представленные выше четыре вектора равны!  

То есть, если мы будем при помощи параллельного переноса перемещать данный нам вектор, то всегда получим вектор равный исходному. Таким  образом, равных векторов может быть бесчисленное множество.

Обозначение векторов

Вектор может быть обозначен латинскими заглавными буквами, например:

При данной форме записи сначала записывается буква обозначающая начало вектора, затем буква обозначающая конец вектора.

Ещё вектор обозначается одной буквой латинского алфавита (прописной):

Возможно также обозначение без стрелок:

Сумма векторов

Суммой двух векторов АВ и ВС будет являться вектор АС.

Записывается как АВ+ВС=АС.

Это правило называется – правилом треугольника.

То есть, если мы имеем два вектора – назовём их условно (1) и (2), и конец вектора (1) совпадает с началом вектора (2), то  суммой этих векторов будет вектор, начало которого совпадает с началом вектора (1), а конец совпадает с концом вектора (2).

Вывод: если мы имеем на плоскости два вектора, то всегда сможем найти их сумму. При помощи параллельного переноса можно переместить любой из данных векторов и соединить его начало с концом другого. Например:

Перенесём вектор b, или по-другому – построим равный ему:

Как находится сумма нескольких векторов? По тому же принципу:

* * *

Правило параллелограмма

Это правило является следствием изложенного выше.

Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Построим вектор равный вектору b так, чтобы его начало совпадало с концом вектора a, и мы можем построить вектор, который будет являться их суммой:

Ещё немного важной информации, необходимой для решения задач.

Вектор, равный по длине исходному, но противоположно направленный, обозначается также но имеет противоположный знак:

Эта информация крайне полезна для решения задач, в которых стоит вопрос о нахождении разности векторов. Как видите, разность векторов это та же сумма  в изменнёном виде.

Пусть даны два вектора, найдём их разность:

Мы построили  вектор противоположный вектору b, и нашли  разность.

Координаты вектора

Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала:

То есть,  координаты вектора представляют собой пару чисел.

Если

И координаты векторов имеют вид:

То   c₁= a₁+ b₁     c₂= a₂+ b₂

Если

То   c₁= a₁– b₁      c₂= a₂– b₂

Модуль вектора

Модулем вектора называется его длина, определяется по формуле:

Формула для определения длины вектора, если известны координаты его начала и конца:

Рассмотрим задачи:

Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину разности векторов АО и ВО.

Найдём вектор, который будет являться результатом АО–ВО:

АО–ВО=АО+(–ВО)=АВ

То есть разность векторов  АО и ВО будет являться вектор АВ. А его длина равна восьми.

Ответ: 8

Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ+AD.

Найдём вектор, который будет являться суммой векторов AD и AB. Вектор BC равен вектору AD. Значит AB+AD=AB+BC=AC

Длина вектора AC это длина диагонали ромба АС, она равна 16.

Ответ: 16

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО+ВО.

Найдём вектор, который будет являться суммой векторов АО и ВО. Вектор ВО равен вектору OD, значит

Длина вектора AD это длина стороны ромба. Задача сводится к нахождению гипотенузы в прямоугольном треугольнике AOD. Вычислим катеты:

По теореме Пифагора:

Ответ: 10

Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора АО–ВО.

Найдём вектор, который будет являться результатом АО–ВО:

Длина вектора АВ это длина стороны ромба. Задача сводится к нахождению гипотенузы АВ в прямоугольном  треугольнике AOB. вычислим катеты:

По теореме Пифагора:

Ответ: 10

Стороны правильного треугольника ABC равны 3.

Найдите длину вектора АВ–АС.

Найдём результат разности векторов:

Длина вектора СВ равна трём, так как в условии сказано, что треугольник равносторонний и его стороны равны 3.

Ответ: 3

27663. Найдите длину вектора а(6;8).

Посмотреть решение

27664. Найдите квадрат длины вектора АВ.

Посмотреть решение

27707. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АС.

Посмотреть решение

27708. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину суммы векторов AB и AD.

Посмотреть решение

27709. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов AB и AD.

Посмотреть решение

27711. Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов АО и ВО.

Посмотреть решение

27713. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора АВ.

Посмотреть решение

27715. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–AD.

Посмотреть решение

27716. Диагонали ромба ABCD равны 12 и 16.

Найдите длину вектора АВ–АС.

Посмотреть решение

Стороны правильного треугольника ABC равны 2√3. Найдите длину вектора АВ+АС.

Посмотреть решение

В будущем мы продолжим рассматривать задачи с векторами, не пропустите!  Задания будут связаны с координатами векторов, скалярным произведением.

На этом всё. Успеха вам!

С уважением, Александр

Вступительный экзамен по математике. Преподаватели приглашают первого абитуриента:
— Сколько будет два плюс два?
— Три! — Нет! — Пять! — Нет! — Шесть!
— Неправильно! Да… дурак, но ищущий… берем!
Заходит второй абитуриент:
— Сколько будет два плюс два?
— Три! — Нет! — Три! — Нет! — Три!
— Неправильно! Да… дурак, но настырный… берем!
Заходит третий абитуриент:
— Сколько будет два плюс два?
— Четыре, конечно!
— Да… умный. Но мест уже нет!

P.S: Буду благодарен, если расскажете о статье в социальных сетях.