В этой статье мы обсудим влияние преломления на длину волны при распространении из одной среды в другую с подробными фактами.
Частота волны не меняется при преломлении волны, следовательно, длина волны прямо пропорциональна ее скорости. Поскольку скорость волны изменяется при переходе от сред, соответственно смещается и длина волны.
Влияет ли преломление на длину волны?
Преломление происходит при переходе луча света из среды в другую.
Скорость волны увеличивается при прохождении из более разреженных сред и уменьшается в более плотных средах, что определяет угол преломления. Длина волны зависит от скорости и изменяется параллельно.
Мы знаем, что скорость света c=λf. Для любой волны, распространяющейся из двух разных сред, скорость движения v прямо пропорциональна длине волны, так как частота волны остается неизменным после преломления.
Скорость волны в среде напрямую зависит от показателя преломления среды, через которую она проходит.
n1/n2 = V2/v1
v2/v1= λ2f/ λ1f
Поскольку частота остается постоянной даже после преломления,
v2/v1= λ2/ λ1
Следовательно,
n1/n2= λ2/ λ1
Преломление волны зависит от длины волны, а длина волны обратно пропорциональна показателю преломления среды.
Подробнее о Типы преломления: сравнительный анализ.
Как преломление влияет на длину волны?
Преломление может увеличивать или уменьшать длину волны света или звука, распространяющихся в среде, имеющей более высокую плотность, чем воздух.
Когда волна распространяется в более плотной среде, скорость волны уменьшается и, следовательно, длина волны уменьшается. Длина волны увеличивается, если скорость волны увеличивается при движении в более разреженной среде.
Рассмотрим волну, распространяющуюся от более разреженной среды к более плотной среде и обратно к более разреженной среде, как показано на рисунке ниже.
Скорость волны в более разреженной среде больше и, следовательно, длина волны увеличивается. При переходе в более плотную среду, имеющую несколько больший показатель преломления, скорость волны и длина волны уменьшаются. При входе обратно в более разреженную среду длина волны и скорость волны увеличиваются.
Подробнее о Какова длина волны фотона: как найти, несколько идей и фактов.
Как показатель преломления влияет на длину волны?
Чем плотнее среда, тем меньше скорость волны и, следовательно, длина волны.
Показатель преломления больше для более плотной среды, чем для более разреженной, потому что скорость и пропорционально длина волны волны уменьшаются при прохождении через более плотную среду.
Показатель преломления среды определяется как скорость распространения волны из двух разных сред. Предположим, что свет проходит из среды 1 в среду 2, показатель преломления среды определяется как
n12=n1/n2= λ2/ λ1
Где н1 – показатель преломления среды 1
n2 – показатель преломления среды 2
v1 это скорость света в среде 1
v2 это скорость света в среде 2
Скорость волны равна произведению длины волны на частоту волны.
v=λf
Давайте возьмем пример, чтобы прояснить, как длина волны зависит от показателя преломления среды, через которую она распространяется.
Подробнее о Показатель преломления.
Пример. Рассмотрим волну света, распространяющуюся из воздуха в воду. Если частота волны равна 6*1016 /сек. Вычислите изменение длины волны света.
Данный: f=6 * 1016 / сек
Показатель преломления воздуха n1=1
Показатель преломления воды n2= 1.33
п=с/об
n=c/λf
λ=c/nf
Это показывает, что длина волны обратно пропорциональна показателю преломления среды.
Длина волны света в воздухе была
λ1=с/н1f
λ1=3* 108 /1*6*1016
λ1= 5 * 107= 500 * 10-9=500нм
После преломления длина волны света в воде становится
λ2=с/н2f
λ2=3* 108/ 1.33* 6* 1016
λ2=3.75* 10-7= 375 * 10-9=375нм
Это ясно указывает на то, что по мере увеличения показателя преломления среды длина волны света уменьшалась.
Это означает, что скорость света уменьшается в среде с большим показателем преломления и увеличивается при переходе из среды с более высоким показателем преломления в среду с меньшим показателем преломления.
Почему длина волны влияет на преломление?
Преломление в основном зависит от плотности среды, а также от градиента температуры и давления среды.
При изменении плотности среды различается длина волны и меняется направление распространения волны. Если длина волны увеличивается, угол преломления будет больше.
Когда волна распространяется из более плотной среды в более разреженную, скорость света и, следовательно, длина волны увеличиваются, а угол преломления, возникающий при искривлении луча света, будет больше.
При распространении волны из более разреженной среды в более плотную длина волны будет уменьшаться, а угол преломления, образующийся при искривлении луча света, будет меньше.
Подробнее о Как найти угловое ускорение из угловой скорости: задача и примеры.
Часто задаваемые вопросы
Почему показатель преломления стекла больше, чем у воздуха?
Показатель преломления определяется изменением скорости света при выходе из данной среды.
Скорость света уменьшается в большей степени в стекле по сравнению со скоростью света в воздухе. Следовательно, показатель преломления стекла больше по сравнению с воздухом.
Как изменится преломление, если увеличить частоту волны?
Компания частота остается постоянной при преломлении и обратно пропорционально длине волны.
Если частота увеличивается, то скорость волны уменьшается, и волна отклоняется к нормали, создавая небольшой угол преломления.
Когда луч света рассеивается после преломления?
Если белый свет проходит через среду и выходит под тем же углом, то дисперсии света не происходит.
Если все компоненты света исходят из среды под разными углами, то это явление называется дисперсией света.
Почему частота света не меняется при распространении из среды с более высокой плотностью?
Скорость света уменьшается при движении из более плотной среды.
Частота определяет распространение света во времени. По мере уменьшения скорости длина волны также будет уменьшаться, поэтому частота остатки постоянная.
Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
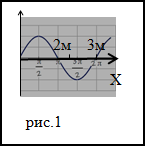
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.
Загрузить PDF
Загрузить PDF
Длина волны – это расстояние между двумя соседними точками, которые колеблются в одной фазе; как правило, понятие “длина волны” ассоциируется с электромагнитным спектром.[1]
Метод вычисления длины волны зависит от данной информации. Воспользуйтесь основной формулой, если известны скорость и частота волны. Если нужно вычислить длину световой волны по известной энергии фотона, воспользуйтесь соответствующей формулой.
-
1
Воспользуйтесь формулой для вычисления длины волны. Чтобы найти длину волны, разделите скорость волны на частоту. Формула:
[2]
-
2
Используйте соответствующие единицы измерения. Скорость измеряется в единицах метрической системы, например, в километрах в час (км/ч), метрах в секунду (м/с) и так далее (в некоторых странах скорость измеряется в британской системе, например, в милях в час). Длина волны измеряется в нанометрах, метрах, миллиметрах и так далее. Частота, как правило, измеряется в герцах (Гц).[3]
- Единицы измерения конечного результата должны соответствовать единицам измерения исходных данных.
- Если частота дана килогерцах (кГц), или скорость волны в километрах в секунду (км/с), преобразуйте данные значения в герцы (10 кГц = 10000 Гц) и в метры в секунду (м/с).
-
3
Известные значения подставьте в формулу и найдите длину волны. В приведенную формулу подставьте значения скорости и частоты волны. Разделив скорость на частоту, вы получите длину волны.[4]
- Например. Найдите длину волны, распространяющейся со скоростью 20 м/с при частоте колебаний 5 Гц.
-
4
Реклама
-
1
-
2
Перепишите представленную формулу, чтобы найти длину волны. Для этого проделайте ряд математических операций. Обе стороны формулы умножьте на длину волны, а затем обе стороны разделите на энергию; вы получите формулу:
. Если энергия фотона известна, можно вычислить длину световой волны.[7]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
- Эту формулу можно использовать для вычисления максимальной длины световой волны, необходимой для ионизации металлов. В формулу подставьте энергию, необходимую для ионизации, и вычислите длину волны.[8]
-
3
В полученную формулу подставьте известные значения и вычислите длину волны. В формулу подставьте только значение энергии, потому что две константы являются постоянными величинами, то есть не меняются. Чтобы найти длину волны, перемножьте константы, а затем результат разделите на энергию.[9]
- Например. Найдите длину световой волны, если энергия фотона равна 2,88 x 10-19 Дж.
Реклама
-
1
Проверьте ответ. Для этого умножьте длину волны на частоту. Если вы получите данное значение скорости, решение правильное; в противном случае проверьте вычисления. Если вы пользуетесь калькулятором, правильно вводите числа.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
- Решите эту задачу как описано выше и получите значение 4,9 м.
- Проверьте ответ: 4,9 м х 70 Гц = 343 м/сек. Это данная в условии задачи скорость, поэтому решение верное.
- Например. Найдите длину волны, которая распространяется со скоростью 343 м/с при частоте колебаний 70 Гц.
-
2
Используйте экспоненциальную запись чисел, чтобы избежать ошибок при округлении чисел (в калькуляторе). Порой в вычислении длины волны участвуют очень большие числа, особенно когда присутствует скорость света. Это может привести к ошибкам округления чисел. Поэтому используйте экспоненциальную запись чисел.[10]
- Например. Свет проходит сквозь воду со скоростью 225000000 м/с. Найдите длину световой волны, если ее частота равна 4 x 1014 Гц.
-
3
Помните, что частота волны не меняется при изменении среды ее распространения. Во многих задачах волна распространяется в двух средах, и некоторые учащиеся пытаются вычислить две длины волны. Это ошибка, потому что в отличие от скорости распространения и длины волны частота волны не меняется при изменении среды ее распространения.[11]
- Например, световая волна длиной λ, распространяющаяся со скоростью v при частоте f, переходит из воздушного пространства в некоторую среду, показатель преломления которой равен 1,5. Как изменятся указанные три величины?
Реклама
Об этой статье
Эту страницу просматривали 158 038 раз.
Была ли эта статья полезной?
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
;
- как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 





Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 


Для электромагнитных волн в вакууме скорость 



Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где
— показатель преломления среды;
— относительная диэлектрическая проницаемость среды;
— относительная магнитная проницаемость среды.
Величины 









Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением 

Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 

- частота:
- длина волны:
- где
— постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару 

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в
, и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
Решение. При попадании света на тонкий стеклянный клин свет частично преломляется, частично отражается как от верхней, так и от нижней поверхности. Световые пучки приобретают разность хода, которая зависит от толщины клина и показателя преломления. Свет падает нормально толщина клина мала, интерференционная картина в отраженном свете локализована на верхней поверхности клина.
При вычислении разности фаз между колебаниями в лучах 1 и 2 нужно, кроме оптической разности хода δ учесть изменение фазы при отражении в т. С.
Так как вокруг клина воздух, то показатель преломления клина n > n0 = 1 (n0 – показатель преломления воздуха). Поэтому луч 1 при отражении теряет полволны λ/2, а луч 2 нет.
Определим оптическую разность хода для лучей 1 и 2 в точке С. Запишем формулы для определения оптической разницы для смежных интерференционных минимумов.
[ begin{align}
& delta =2cdot dcdot sqrt{n_{2}^{2}-{{sin }^{2}}alpha }-frac{lambda }{2} (1). alpha =90, delta =2cdot dcdot n-frac{lambda }{2} (2). \
& {{delta }_{1}}=2cdot {{d}_{1}}cdot n-frac{lambda }{2} (3), {{delta }_{2}}=2cdot {{d}_{2}}cdot n-frac{lambda }{2} (4). \
end{align} ]
[ begin{align}
& delta =(2cdot k+1)cdot frac{lambda }{2} (5), {{delta }_{1}}=(2cdot k+1)cdot frac{lambda }{2} (6), {{delta }_{2}}=(2cdot (k+1)+1)cdot frac{lambda }{2}, \
& {{delta }_{2}}=(2cdot k+3)cdot frac{lambda }{2} (6). \
& (2cdot k+1)cdot frac{lambda }{2} =2cdot {{d}_{1}}cdot n-frac{lambda }{2} , {{d}_{1}}=frac{lambda cdot k}{2cdot n}+frac{lambda }{2cdot n} (7), \
& (2cdot k+3)cdot frac{lambda }{2} =2cdot {{d}_{2}}cdot n-frac{lambda }{2}, {{d}_{2}}=frac{lambda cdot k}{2cdot n}+frac{2cdot lambda }{2cdot n} (8). \
end{align}
]
Где: d1 и d2 толщины клина, соответствую¬щие соседним полосам.
Вычтем из (8 ) (7):
[ begin{align}
& Delta d={{d}_{2}}-{{d}_{1}}=frac{lambda }{2cdot n} (9), frac{Delta d}{l}=sin alpha approx tgalpha (10), frac{lambda }{2cdot ncdot l}=tgalpha ,lambda =2cdot ncdot lcdot tgalpha . \
& lambda =2cdot 1,4cdot 0,25cdot {{10}^{-2}}cdot tg20=0,2548cdot {{10}^{-2}}cdot 5,81cdot {{10}^{-3}}=4,067cdot {{10}^{-5}}. \
end{align}
]
Если угол 20”, то ответ 6,755∙10-7 м.
Ответ: если 20’, то ответ 4,067∙10-5 м, если 20”, то ответ 6,755∙10-7 м.