Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе.
Обозначают длину волны, чаще всего буквой $lambda$ .
Для синусоидальных волн $lambda$ – это расстояние, на которое волна распространяется за один период
(T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$lambda=v T=frac{v}{nu}=frac{2 pi}{k}$$
где v – скорость распространения волны, $nu=frac{1}{T}$ – частота колебаний,
$k=frac{omega}{v}$ – волновое число,
$T=frac{2 pi}{omega}$ – период волны,
$omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($lambda_{st}$) называют расстояние в пространстве между
двумя пучностями (или узлами):
$$lambda_{s t}=frac{pi}{k}=frac{lambda}{2}(2)$$
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и
узлом связывает равенство:
$$frac{lambda_{s t}}{2}=frac{lambda}{4}(3)$$
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$lambda=frac{v_{p h}}{nu}(4)$$
Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии
$Delta x$ имеют при колебании разность
фаз ($Delta varphi$), которая равна:
$$Delta varphi=frac{2 pi Delta x}{lambda}(5)$$
Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме
($c approx 3 cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в
вакууме, может быть рассчитана при помощи формулы:
$$lambda=c T=frac{c}{nu}(6)$$
Длина электромагнитной волны в веществе равна:
$$lambda=frac{c}{n nu}(7)$$
где $n=sqrt{varepsilon mu}$ – показатель преломления вещества,
$varepsilon$ – диэлектрическая проницаемость вещества,
$mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$lambda$]=м
В СГС: [$lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду,
которая имеет диэлектрическую проницаемость $varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную
проницаемость вещества равной единице ($mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$lambda_{1}=frac{c}{nu}(1.1)$$
Длина волны в веществе:
$$lambda_{2}=frac{c}{n nu}=frac{c}{sqrt{varepsilon mu} cdot nu}(1.2)$$
Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$Delta lambda=lambda_{2}-lambda_{1}=frac{c}{sqrt{varepsilon mu} cdot nu}-frac{c}{nu}=frac{c}{nu}left(frac{1}{sqrt{varepsilon mu}}-1right)$$
Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что
$c approx 3 cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$Delta lambda=frac{3 cdot 10^{8}}{10^{6}}left(frac{1}{sqrt{4 cdot 1}}-1right)=-1,5 cdot 10^{2}(mathrm{~m})$$
Ответ. Длина волны уменьшится на 150 м
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
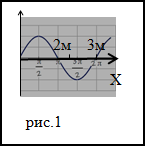
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые
находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной
$Delta varphi=frac{3 pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
Основой для решения задачи будет формула:
$$Delta varphi=frac{2 pi Delta x}{lambda}=frac{2 pileft(x_{2}-x_{1}right)}{lambda}(2.1)$$
Выразим из (2.1) искомую длину волны, получим:
$$lambda=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi}(2.2)$$
Период колебаний связан с длиной волны формулой:
$$T=frac{lambda}{v}(2.3)$$
C учетом (2.2), имеем:
$$T=frac{2 pileft(x_{2}-x_{1}right)}{Delta varphi v}$$
Проведем вычисления:
$$
begin{array}{c}
lambda=frac{2 pi(3-2)}{3 pi} cdot 5=frac{10}{3}(m) \
T=frac{10}{3 cdot 2}=1,67(c)
end{array}
$$
Ответ. $lambda approx 3,3 mathrm{~m} ; T approx 1,67 mathrm{c}$
Читать дальше: Формула количества теплоты.
График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе[1][2].
Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π[3].
Длину волны можно также определить:
- как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на
; - как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
- как пространственный период волнового процесса.
Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву 
, размерность длины волны — метр ([м]).
Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.
Длина волны — пространственный период волнового процесса[править | править код]
Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с периодом колебаний 
[с] (интервалом времени, за который периодический колебательный процесс повторяется и размерность которого — секунда), длину волны [м] можно рассматривать как пространственный период волнового процесса. Следует заметить, что круговой частоте колебания 
[радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с в фиксированной точке (в множестве точек если твердое тело), соответствует «пространственная круговая частота» 
[радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках пространства, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в [м], отличаются ровно на 
.
Связь с частотой[править | править код]
Получить соотношение, связывающее длину волны с фазовой скоростью 
и частотой 
можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду колебаний, поэтому
Для электромагнитных волн в вакууме скорость в этой формуле равна скорости света (299 792 458 м/с), и длина волны
. Если значение подставить в герцах, то будет выражена в метрах.
Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства. Магнитная антенна средневолнового радиоприёмника имеет габарит на порядки меньше длины волны, и при этом, тем не менее, обладает пространственной селективностью.
Длина волны в среде[править | править код]
В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.
Длина электромагнитной волны в среде короче, чем в вакууме:
- где — показатель преломления среды;
- — относительная диэлектрическая проницаемость среды;
- — относительная магнитная проницаемость среды.
Величины 
, 
и 
могут существенно зависеть от частоты 
(явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне 
(для диэлектриков 
, для ферромагнетиков с ростом частоты 
), то в инженерной практике используют величину 
, которую называют коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) = 2,56, и коэффициент укорочения 
= 1/1,6 = 0,625.
Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением , но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же .
Волны де Бройля[править | править код]
Волнам де Бройля также соответствует определённая длина волны. Частице с энергией 
и импульсом 
, соответствуют:
- частота:
- длина волны:
- где — постоянная Планка.
Примеры[править | править код]
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 000 делим на частоту в килогерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару ↔ , например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м
Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) —
33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм[4].
Примечания[править | править код]
- ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в , и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine
Литература[править | править код]
- Волны де Бройля / В. И. Григорьев // Вешин — Газли. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 5).
- Длина волны // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
Основные формулы по физике – КОЛЕБАНИЯ И ВОЛНЫ
При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.
Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.
Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.
Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.
Смотрите также основные формулы квантовой физики
Таблица формул: колебания и волны
|
Физические законы, формулы, переменные |
Формулы колебания и волны |
||||
|
Уравнение гармонических колебаний: где х – смещение (отклонение) колеблющейся величины от положения равновесия; А – амплитуда; ω – круговая (циклическая) частота; t – время; α – начальная фаза; (ωt+α ) – фаза. |
|
||||
|
Связь между периодом и круговой частотой: |
|
||||
|
Частота: |
|
||||
|
Связь круговой частоты с частотой: |
|
||||
|
Периоды собственных колебаний 1) пружинного маятника: где k – жесткость пружины; 2) математического маятника: где l – длина маятника, g – ускорение свободного падения; 3) колебательного контура: где L – индуктивность контура, С – емкость конденсатора. |
|||||
|
Частота собственных колебаний: |
|
||||
|
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А1 и А2 – амплитуды составляющих колебаний, α1 и α2 – начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания |
|
||||
|
Уравнение затухающих колебаний: е = 2,71… – основание натуральных логарифмов. |
|
||||
|
Амплитуда затухающих колебаний: где А0 – амплитуда в начальный момент времени; β – коэффициент затухания; t – время. |
|
||||
|
Коэффициент затухания: колеблющегося тела где r – коэффициент сопротивления среды, m – масса тела; колебательного контура где R – активное сопротивление, L – индуктивность контура. |
|
||||
|
Частота затухающих колебаний ω: |
|
||||
|
Период затухающих колебаний Т: |
|
||||
|
Логарифмический декремент затухания: |
|
||||
|
Связь логарифмического декремента χ и коэффициента затухания β: |
|
||||
|
Амплитуда вынужденных колебаний где ω – частота вынужденных колебаний, fо – приведенная амплитуда вынуждающей силы, при механических колебаниях: при электромагнитных колебаниях: |
|
||||
|
Резонансная частота |
|
||||
|
Резонансная амплитуда |
|
||||
|
Полная энергия колебаний: |
|
||||
|
Уравнение плоской волны: где ξ – смещение точек среды с координатой х в момент времени t; k – волновое число: |
|
||||
|
Длина волны: где v скорость распространения колебаний в среде, Т – период колебаний. |
|
||||
|
Связь разности фаз Δφ колебаний двух точек среды с расстоянием Δх между точками среды: |
|
Поделитесь ссылкой с друзьями:
Похожие таблицы
Комментарии:
Длина волны. Связь длины волны со скоростью ее распространения. Уравнение волны
Как уже отмечалось, возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит не мгновенно, а с определенной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости (vec upsilon) направлен по нормали к волновой поверхности в сторону распространения волны и в однородной изотропной среде совпадает с направлением луча. Следует отличать скорость распространения волны от скорости колебания частиц среды около своих положений равновесия.
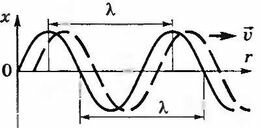
Пусть волна распространяется вдоль горизонтальной оси (например, вдоль упругого горизонтального шнура). В данный момент времени форма волны повторяется в пространстве вдоль шнура через определенные отрезки. На рисунке 15.7 показан профиль волны в определенный момент времени. С течением времени вся эта картина перемещается со скоростью (upsilon) слева направо (штриховая линия).
Расстояние между ближайшими точками, колеблющимися в одинаковых фазах (рис. 15.7), называется длиной волны. Длина волны (~lambda) равна расстоянию, на которое распространяется фронт волны за время, равное периоду (~T) колебаний источника волн[~lambda = upsilon T.]
Так как (T = frac{1}{nu};) (nu = frac{omega}{2 pi},) то скорость волны связана с частотой колебаний уравнением (~upsilon = lambda nu.) Отсюда (lambda = frac{upsilon}{nu} = frac{2 pi upsilon}{omega},) где (~omega) — циклическая частота колебаний, (~nu) и (~omega) зависят только от свойств источника волны.
При возникновении волн в среде их частота определяется частотой колебаний источника, а скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.
Выведем уравнение плоской волны.
Пусть источник совершает гармонические колебания по закону
(~x = A sin omega t,)
где х — смещение, А — амплитуда, (~omega) — циклическая частота, t — время.
В точках, отстоящих на расстоянии r от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать во времени от колебаний источника на (Delta t = frac{r}{upsilon}.)
Тогда смещение точки среды с координатой r в момент времени t
(x = A sin omega Bigr( t-frac{r}{upsilon} Bigl),) или (x = A sin Bigr( omega t-frac{omega r}{upsilon} Bigl).)
Это и есть уравнение плоской бегущей монохроматической волны (при этом предполагают, что затуханием волны в процессе ее распространения можно пренебречь). Смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени t и расстояния r до равновесного положения точки среды.
Из уравнения волны следует:
1. Амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника.
2. Любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления r данной точки от источника колебаний:
(~x = A sin(omega t + alpha),) где (alpha = -frac{omega r}{upsilon}.)
3. Положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением
(x = A sin Bigr( frac{omega r}{upsilon} + beta Bigl),) где (~beta = -omega t)
имеет разное значение в разные моменты времени.
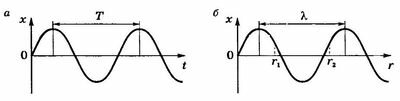
На рисунке 15.8, б приведен график этой функции при t = 0, представляющий собой “моментальный снимок” волны, т.е. положение всех частиц среды, в которой распространяется волна, в момент времени t = 0 — график волны. В отличие от графика колебаний (рис. 15.8, а), который показывает зависимость смещения одной частицы от времени в данной точке среды, график волны (рис. 15.8, б) показывает зависимость смещения всех частиц среды из положения равновесия от расстояния г до источника колебаний в некоторый фиксированный момент времени.
Найдем разность фаз колебаний двух точек среды, находящихся на расстоянии (~Delta r = r_2 – r_1) друг от друга (рис. 15.8, б). Колебания этих точек описываются уравнениями:
(x_1 = A sin omega Bigr( t – frac{r_1}{upsilon} Bigl);) (x_2 = A sin omega Bigr( t – frac{r_2}{upsilon} Bigl).)
Разность фаз (Delta varphi_1 = varphi_1 – varphi_2) будет равна
(Delta varphi = omega Bigr( t – frac{r_1}{upsilon} Bigl) – omega Bigr( t – frac{r_2}{upsilon} Bigl) = frac{omega}{upsilon}(r_2-r_1) = frac{2 pi}{T upsilon}(r_2 – r_1) = frac{2 pi}{lambda} Delta r.)
Если две точки находятся на расстоянии (~Delta r = lambda,) то разность фаз колебаний этих точек (Delta varphi = 2 pi,) что соответствует данному выше определению длины волны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 428-430.
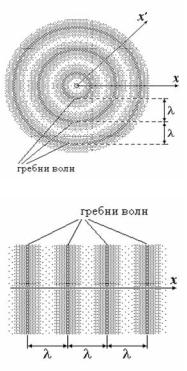
Рис. 6.17
Рис. 6.18
|
6.8. Механические волны |
381 |
6.8.2. Виды волн
Вид волн определяется источником колебания. Если источник колебаний очень мал (точечный источник), то волны от него радиально расходятся во все стороны, как это показано на рис. 6.17.
Радиальная прямая, проведенная от точечного источника, вдоль которой распространяется волна, называется лучом. Волновая поверхность от точечного источника имеет форму сферы. Такая волна называется
сферической.
В изотропной среде (т. е. среде, свойства которой не зависят от направления), волновой вектор перпендикулярен волновой поверхности.
Если источник колебаний — протяженная плоскость, то волновая поверхность имеет форму плоскости. Такая волна называется плоской. В плоской волне все лучи, вдоль которых она распространяется, параллельны друг другу, например, параллельны оси х (рис. 6.18).
В однородной среде колебание вдоль всех параллельных лучей распространяется с одинаковой фазовой скоростью u.
Кроме плоских и сферических волн можно выделить также волны цилиндрические, у которых вол-
новые поверхности — концентрические цилиндры. Такие волны возбуждаются нитевидными или щелевыми источниками.
Среди волн разнообразной физической природы выделяют помимо упругих волн и волн на поверхности жидкости, электромагнитные и плазменные волны. Особенно большое значение в природе и технике играют электромагнитные волны.
|
382 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
6.8.3. Уравнение плоской гармонической волны
Уравнением плоской гармонической волны называется периодическая функция ξ = ξ(x, C, z,t) , позволяющая найти смещение от положения равновесия частицы волнового поля в любой момент времени.
РассмотримG случай, когда плоская волна распространяется со скоростью u в однородной изотропной среде в направлении оси х (рис. 6.19). Смещение частицы зависит от времени t и координаты х той волновой поверхности, которой эта частица принадлежит
ξ= ξ(x,t) .
Внашем примере Gлучом является ось х. Пусть волна распространяется со скоростью u . Если волна гармоническая, то в каждой точке пространства частица совершает гармоническое колебание.
Пусть колебания частиц, принадлежащих волновой поверхности
скоординатой х = 0, описываются уравнением
|
ξ(0,t) = Acos ωt . |
(6.51) |
Колебания частиц с координатой х начнутся позже, так как требуется время t для того, чтобы волна прошла расстояние х от колеблющейся точки до источника колебаний. Время прохождения волной этого расстояния равно
τ = ux .
Следовательно, колебания частиц с координатой х будут отставать по времени от колебаний частиц с координатой х = 0 на τ:
|
ξ(x,t) = Acos ω(t − τ) , |
||||
|
или |
||||
|
ξ(x,t) = Acos ω(t − |
x |
) = Acos(ωt − |
ω x) = Acos(ωt − kx) , |
(6.52) |
|
u |
u |
ω x — |
||
|
где А — амплитуда колебаний или амплитуда волны, ϕ = ωt − |
||||
|
u |
фаза колебаний волны в произвольной точке с координатой х, k — модуль волнового вектора (см. 6.50). Волновой вектор указывает на направление распространения волны.
Равенство (6.52) называется уравнением плоской гармонической волны.
|
6.8. Механические волны |
383 |
Фазы колебаний в разных точках среды отличаются. Вычислим разность фаз в двух точках среды, определяемых координатами х1 и
|
х2. Фазы колебании в точках х1 и х2 имеют вид |
|||||||||||||||
|
ϕ = ωt − |
ω x , |
ϕ |
= ωt − ω x . |
||||||||||||
|
Разность фаз |
1 |
u |
1 |
2 |
u |
2 |
|||||||||
|
ϕ = ϕ − ϕ |
= (ωt − |
ω x ) − (ωt − |
ω x ) = |
||||||||||||
|
1 |
2 |
u 1 |
u |
2 |
|||||||||||
|
= − |
ω x |
+ ω x |
= |
ω |
(x |
− x ) = |
2π |
x = |
2π |
x. |
|||||
|
u |
Tu |
λ |
|||||||||||||
|
u 1 |
u |
2 |
2 |
1 |
Уравнение (6.52) называют уравнением прямой волны. Уравнение плоской гармонической волны, распространяющейся
в направлении, противоположном направлению оси х, имеет вид
ξ(x,t) = Acos(ωt + kx) .
Это уравнение обратной волны.
Уравнение плоской гармонической волны, распространяющейся
|
в произвольном направлении, имеет вид |
||
|
G |
GG |
(6.53) |
|
ξ(r,t) = Acos(ωt − kr ) , |
rG — радиус-вектор, определяющий положение рассматриваемой частицы.
Более сложные волны можно представить в виде суперпозиции гармонической волны.
Если в (6.53) зафиксировать t, то зависимость волновой функции от х дает как бы моментальную фотографию волны (застывшую синусоиду), т. е. значение амплитуды колебаний каждой точки в данный момент времени. Пространственный период ее, т. е. расстояние между точками, в которых совпадают значения ξ и значение ее производной по координате, называется длиной волны и обозначается буквой λ (рис. 6.19).
|
График ξ(х) похож на график гармониче- |
|
|
ского колебания, но отличается по сущест- |
|
|
ву. Например, график колебаний в точке В с |
|
|
координатой x дает зависимость плотности |
|
|
среды в этой точке от времени. |
Рис. 6.19 |
384 Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
|
Картину распространения волны можно |
||
|
представить, если застывшую синусоиду на |
||
|
рис. 6.19 привести в движение вдоль оси х со |
||
|
скоростью uG . |
||
|
Две последовательные «моментальные фо- |
||
|
тографии» волны в моменты времени t и t + t |
||
|
Рис. 6.20 |
показаны на рис. 6.20. Точка волны с опреде- |
|
|
ленной фазой, (например, точка максимума |
||
функции ξ на рис. 6.20) смещается за это время на расстояние u t.
Длина волны λ = uT = 2kπ .
Зависимость ξ = ξ(x,t) можно найти, решая волновое уравнение. Волновое уравнение — дифференциальное уравнение с частными производными 2-го порядка от смещения и времени, описывающее процесс распространения возмущений в упругой среде. Оно связывает вторые частные производные от смещения по координатам со вторыми частными производными от смещения по времени. Если продифференцировать (6.52) дважды по времени, затем дважды по координате, то получим
|
∂2ξ(x,t) |
= − Aω2 |
cos(ωt − kx), |
||||||||
|
∂t2 |
||||||||||
|
∂2ξ(x,t) |
= − Ak 2 |
cos(ωt − kx). |
||||||||
|
∂x2 |
||||||||||
|
Разделив второе уравнение на первое, получим |
||||||||||
|
∂2ξ(x,t) |
= |
k 2 |
∂2ξ(x,t) |
. |
||||||
|
∂x2 |
ω2 |
∂t2 |
||||||||
|
Учитывая, что |
k 2 |
= |
1 |
, запишем дифференциальное волновое |
||||||
|
ω2 |
u2 |
|||||||||
уравнение плоской гармонической волны, распространяющейся в направлении оси х:
|
∂2ξ(x,t) |
= |
1 ∂2ξ(x,t) |
. |
(6.54) |
|
∂x2 |
u2 ∂t2 |
|||
|
Дифференциальное уравнение (6.54) |
позволяет решить простые |
задачи, связанные с распространением волны. Например, можно получить скорость распространения волны в натянутой струне.
|
6.8. Механические волны |
385 |
Если волна распространяется в произвольном направлении, то в левой части волнового уравнения появляются слагаемые, содержащие вторые частные производные по у и z
∂2ξ + ∂2ξ + ∂2ξ = 1 ∂2ξ
∂x2 ∂y2 ∂z2 u2 ∂t2 .
Решением этого уравнения в зависимости от дополнительных условий могут быть уравнения ξ = ξ(x, y, z,t) плоской, сферической, цилиндрической или других волн.
Скорость волны зависит от свойств среды, в которой волна распространяется (в частности, от плотности ρ и коэффициентов, характеризующих упругость среды).
Приведем без доказательства примеры формул для расчета скорости распространения волны в разных средах, которые могут быть полезны при решении конкретных задач.
1. В растянутой струне скорость распространения поперечной волны зависит от силы натяжения струны FT и от массы, приходящейся
|
на единицу длины струны, ( |
m |
= |
ρSl = ρS , где ρ — плотность мате- |
|
|
l |
l |
|||
|
риала, S — площадь поперечного сечения, l — длина струны) |
||||
|
u = |
FT |
. |
||
|
ρS |
2. Скорость распространения продольной волны в твердом тонком
|
стержне вычисляется по формуле |
|||
|
u = |
E |
, |
|
|
ρ |
|||
где Е — модуль Юнга (модуль продольной упругости материала). 3. Скорость распространения поперечной волны в твердом теле
u = Gρ ,
где G — модуль сдвига среды.
4. Скорость распространения звуковой волны в идеальном газе
|
u = |
kRT |
, |
|
|
μ |
|||
где k — показатель адиабаты, Т — температура, R — универсальная газовая постоянная, μ — молярная масса газа.
|
386 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
6.8.4. Интерференция волн
Если в среде имеется не один, а несколько источников волн, то на каждую точку среды воздействуют одновременно несколько волновых движений. Если волны имеют одинаковую циклическую частоту и накладываются друг на друга, то наблюдается явление интерференции.
Интерференция — наложение волн, при котором колебания, обусловленные этими волнами, в одних местах усиливают друг друга, а в других — ослабляют.
Интерферировать могут лишь когерентные волны.
Две волны называются когерентными, если разность их фаз в каждой точке волнового поля остается неизменной.
Источники таких волн называются когерентными. Рассмотрим наложение волн от двух когерентных источников.
Пусть из двух когерентных источников, расположенных на некотором расстоянии друг от друга, генерируют сферические поперечные гармонические волны в одинаковых фазах. В произвольной точке, отстоящей от источников на расстояния r1 и r2, волны, создаваемые этими источниками, будут сдвинуты по фазе из-за того, что r1 ≠ r2 . Результирующее колебание в заданной точке равно сумме составляющих колебаний
ξ(r,t) = ξ(r1 ,t) + ξ(r2 ,t) = A1 cos(ωt − kr1 ) + A2 cos(ωt − kr2 ) , где А1 и А2 — амплитуды волн, k — волновое число.
Разность фаз волн в заданной точке равна
ϕ2 − ϕ1 = (ωt − kr2 ) − (ωt − kr1 ) = kr1 − kr2 = k(r1 − r2 ) .
Согласно уравнению (6.23) результирующая амплитуда в заданной точке
A = A12 + A22 + 2A1 A2 cos(ϕ2 − ϕ1 ) .
Если ϕ2 − ϕ1 = ±2nπ , где n = 0, 1, 2,……., то А = А1 + А2, т. е. интерферирующие волны максимально усиливают друг друга.
Если ϕ2 − ϕ1 = ±(2n + 1)π , то A = A1 − A2 , т. е. интерферирующие волны максимально ослабляют друг друга. В частности, при А1 = А2 волны полностью гасят друг друга. При всех прочих значениях разности фаз волны лишь частично усиливают или ослабляют друг друга.
|
6.8. Механические волны |
387 |
6.8.5. Стоячие волны
Волна, получающаяся при интерференции двух встречных плоских волн с одинаковыми частотами и амплитудами, называется стоячей.
Стоячая волна возникает при отражении плоской волны от какихлибо преград, например от поверхности раздела двух сред.
Уравнение плоской синусоидальной стоячей волны получается в результате сложения прямой ( ξ1 = Acos(ωt − kx) ) и обратной ( ξ2 = Acos(ωt + kx) ) волн, распространяющихся вдоль оси х.
ξ(x,t) = ξ1 (x,t) + ξ2 (x,t) = Acos(ωt − kx) + Acos(ωt + kx) = = 2Acos kx cos ωt.
Величина A(x) = 2Acos kx — амплитуда стоячей волны. Амплитуда зависит от координаты х.
Вточках, где kx = ±nπ (n = 0,1, 2,…) , амплитуда максимальна по абсолютной величине. Эти точки называются пучностями стоячей волны.
Вточках, где kx = ±(n + 12)π , амплитуда стоячей волны равна
нулю.
Эти точки называются узлами стоячей волны.
|
Учитывая, что k = |
2π |
, найдем координаты пучностей и узлов |
|||||||||||
|
λ |
|||||||||||||
|
nπ |
= ±n λ ; |
||||||||||||
|
x |
= ± |
||||||||||||
|
пучн |
k |
2 |
|||||||||||
|
1 |
π |
||||||||||||
|
n + |
2 |
1 λ |
|||||||||||
|
xузл |
= ± |
= ± n + |
. |
||||||||||
|
k |
|||||||||||||
|
2 2 |
Расстояние между соседними пучностями так же, как и расстоя-
λ
ние между соседними узлами, равно 2 .
Фазы колебаний частиц, лежащих по разные стороны от узла, отличаются на π. Все частицы, находящиеся между узлами, колеблются в одинаковых фазах: все одновременно достигают крайних положений и одновременно проходят через нуль, но амплитуды колебаний этих частиц разные. На рис. 6.21 изображено мгновенное отклонения частиц от положения равновесия в стоячей волне.
|
388 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Примером стоячей волны могут служить колебания струны. В местах закрепления струны всегда образуются узлы, поэтому в струне возможны
Рис. 6.21 только такие колебания, половина длины волны которых укладывается на длине струны A целое число раз
A = n λ2n ,
где n = 1, 2, 3, … Длины волн λn соответствуют частотам колебаний струны
|
νn = |
u |
= |
u |
n , |
|
|
λn |
2A |
||||
где u — фазовая скорость распространения колебаний вдоль струны. Частота, соответствующая n = 1, называется основной частотой струны. Частоты, соответствующие n = 2, 3, …, называются обертонами. В общем случае колебания струны складываются из колебаний основной частоты и обертонов.
Вопросы и задания для самопроверки
1.Как выразить через длину волны λ расстояние b между ближайшими точками на луче распространения волны, в которых фазы противоположны (например, между положительным и отрицательным максимумами)?
2.Как выразить параметры k и λ через циклическую ω и линейную ν частоты?
3.Какова длина бегущей волны, если разность фаз колебаний то-
π?Δϕ =
6
4.Какая из указанных величин (длина волны, скорость распространения волны, частота колебаний) изменяется при переходе волн из одной среды в другую?
5.Докажите, что стоячая волна ξ(x,t) = 2Acos kx cos ωt является результатом сложения двух противоположно направленных гармо-
|
6.8. Механические волны |
389 |
нических волн одинаковой амплитуды и одинаковой циклической частоты.
6.Волны какого типа будут возбуждены в горизонтальном металлическом стержне, если ударить по концу молотком: а) сбоку; б) в торец?
7.Почему не могут быть поперечными упругие волны в газе?
8.Если известно, что из одной области среды в другую переносится энергия, то как определить, переносится ли она волнами или частицами вещества?
9.Обладает ли волновым фронтом плоская гармоническая вол-
на?
10.Может ли существовать в природе плоская гармоническая волна или это физическая идеализация, лишь приближенно описывающая реальность?
11.В чем различие бегущих и стоячих волн, плоских и сферических волн, продольных и поперечных волн?
Примеры решения задач
Задача 6.16
Длина волны λ = 5 м, частота колебаний ν = 3 Гц. Чему равна скорость u распространения волны?
Дано: λ = 5 м; ν = 3 Гц. Найти: u.
По условию задачи три полных колебания совершаются за время t = 1 с, т. е. за одну секунду через данную точку выбранной оси, вдоль которой распространяется волна, пройдут три гребня волны, отстоящие друг от друга на расстояние λ. Первый гребень (или любая другая фиксированная точка волны) переместится за одну секунду на расстояние 3 λ. Следовательно, скорость распространения вол-
ны u = 3λ . Подставив числовые значения, получим t = 3 15 =
u 45 м/с.
1
Ответ: скорость распространения волны u = 45 м/с.
|
390 |
Глава 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ |
Задача 6.17
На каком расстоянии A находятся две ближайшие точки в воде, совершающие колебания в противоположных фазах, если частота колебаний ν = 725 Гц, скорость звука в воде u = 1450 м/с.
Дано: u = 1450 м/с; ν = 725 Гц. Найти: A.
Две ближайшие точки, колеблющиеся в противофазе, находятся
|
на расстоянии A = |
λ |
, где λ — длина волны. |
||||||
|
2 |
u |
|||||||
|
Длина волны |
λ = uT = |
, |
||||||
|
ν |
||||||||
|
A = |
u |
= |
1450 |
= 1 м. |
||||
|
2ν |
2 725 |
Ответ: две ближайшие точки, колеблющиеся в противофазе, находятся на расстоянии 1 м.
Задача 6.18
Две точки, находящиеся на прямой на расстояниях х1 = 12 м и х2 = 15 м от источника волн, колеблются с разностью фаз Δφ = 0,75π. Найти длину волны λ, смещения указанных точек ξ(x1 ,t1 ) , ξ(x2 ,t1 ) в момент времени t1 = 1,2 и уравнение волны ξ(x,t) , если амплитуда колебаний A = 0,1 м, скорость распространения волны u = 20 м/с.
Дано: u = 20 м/с; Δφ = 0,75π; t = 1,2 с; А = 0,1 м; х1 = 12 м; х2 = 15 м. Найти: λ, ξ(x1 ,t1 ) , ξ(x2 ,t1 ) , ξ(x,t) = Asin ω(t − ux) .
Точки, находящиеся друг от друга на расстоянии, равном длине волны λ, колеблются с разностью фаз, равной 2π; точки, находящиеся друг от друга на любом расстоянии x, колеблются с разно-
|
стью фаз, равной |
x2 − x1 |
||||||||
|
ϕ = |
x |
2π = |
2π . |
||||||
|
λ |
|||||||||
|
λ |
|||||||||
|
Решая это равенство относительно λ, получим |
|||||||||
|
λ = |
2π |
(x |
− x ) . |
||||||
|
ϕ |
2 |
1 |
|||||||
|
Подставив численные значения, получим |
|||||||||
|
λ = |
2π |
(15 − 12) = 8 м. |
|||||||
|
0, 75π |
|||||||||
