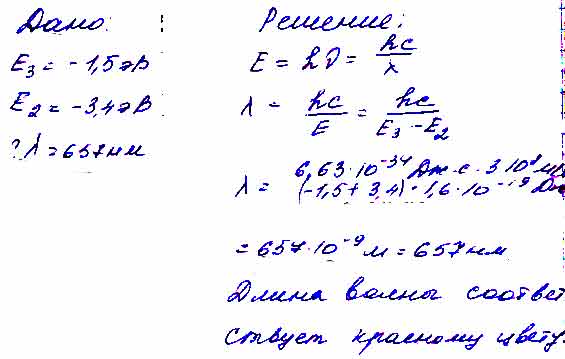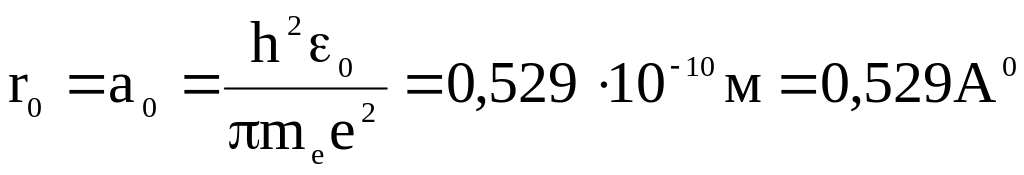Как найти длину волны излучения атома водорода

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

UCHEES.RU – помощь студентам и школьникам

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

---

2020 – 2023 – UCHEES.RU

Как определить максимальную длину волны?

Цель
работы:
проградуировать монохроматор по спектру
ртути, определить длины волн видимой
части спектра водорода.

Приборы
и принадлежности:
монохроматор УМ-2, ртутная лампа,
водородная лампа, блок питания.

Теоретические
сведения

(1)

Все
нагретые тела являются источниками
электромагнитного излучения. Совокупность
длин волн электромагнитного излучения,
испускаемых источни­ком, называется
спектром его излучения. Характер спектра
излучения опреде­ляется температурой
и природой источника.

Твердые
и жидкие тела излучают все длины волн
(сплошной спектр). Разреженные газы и
пары (возбужденные атомы) дают излучение,
состоя­щее из отдельных линий
(линейчатый спектр). Распределение этих
линий в спектре для большинства атомов
очень сложно. Исключение представляют
спектры атома водорода и водородоподобных
ионов. Они представляют собой отделенные
друг от друга серии (группы) линий в
инфракрасной, видимой и ультрафиолетовой
областях спектра электромагнитного
излучения.

Наиболее
простой линейчатый спектр – спектр
атомарного водорода – со­стоит из
нескольких серий: серии Лаймана в
ультрафиолетовой области, серии Бальмера
в видимой и ближней ультрафиолетовой
области, серий Пашена, Брэ­кета и
Пфунда в инфракрасной области спектра.
Установлено, что закономер­ность
расположения линий в спектре водорода
выражается эмпирической фор­мулой
Бальмера:

(1)

где
ν – частота электромагнитного излучения
наблюдаемой линии; R=3,29·
с^-1
– постоянная Ридберга; m,
n – целые чиcла,
обозначающие серию и номер линии в
серии. В каждой серии m
имеет свое постоянное значение, а n=m+1,
m+2,…

Так
как
,
то формула (1) может быть переписана для
длин волн:

,
(2)

где
R=1,10·10⁷
м^-1
– тоже постоянная Ридберга.

Для
объяснения экспериментальных данных
Нильс Бор, используя плане­тарную
модель атома Резерфорда, создал теорию
атома водорода, основанную на следующих
постулатах.

Первый
постулат Бора (постулат стационарных
состояний): атомы могут длительно
пребывать только в определенных
стационарных состояниях, в кото­рых,
несмотря на происходящие в них движения
заряженных частиц, они не из­лучают
и не поглощают энергию. В этих состояниях
атомы обладают энергия­ми, образующими
дискретный ряд E₁,
Е₂,
Е₃,..Е_n.
Состояния эти характеризу­ются своей
устойчивостью, всякое изменение энергии
в результате поглощения или испускания
электромагнитного излучения, или в
результате соударения, может происходить
только при полном переходе (скачком) из
одного состояния в другое.

Правило
квантования орбит Бора утверждает, что
в стационарном состоя­нии атома
электрон, двигаясь по круговой орбите,
должен иметь квантованные (дискретные)
значения момента импульса, удовлетворяющие
условию

(n=1,
2, 3…), (3)

где
m_е
– масса электрона; V
– скорость электрона; r – радиус его
орбиты; h – постоянная Планка. .

Второй
постулат Бора
(правило частот): при переходе атома из
одного ста­ционарного состояния в
другое испускается или поглощается
один фотон.

Излучение
фотона происходит при переходе атома
из состояния с большей энер­гией в
состояние с меньшей энергией (при этом
электрон с более удаленной от ядра
орбиты переходит на ближнюю к ядру
орбиту). Поглощение фотона сопровож­дается
переходом атома в состояние с большей
энергией (этому соответствует переход
электрона на более удаленную от ядра
орбиту).

Математически
правило частот Бора может быть записано
следующим об­разом:

,
(4)

где
E_n,
E_m
– энергии атома в двух стационарных
состояниях; hν_nm
– энергия из­лученного или поглощенного
фотона. Если Е_n
> Е_m,
происходит излучение фотона, если Е_n
< Е_m
– его поглощение.

Постулаты
Бора противоречат следующим положениям
классической физики:

1. В
   классической механике предполагается,
   что при переходе системы из одного
   энергетического состояния в другое
   энергия системы меняется непрерывно,
   принимая все промежуточные значения.

2. Электрон,
   находясь на круговой орбите, движется
   с центростремительным ускорением,
   следовательно, согласно классической
   электродинамике, он должен излучать
   электромагнитные волны, т. е. терять
   энергию и в конце движения упасть на
   ядро (причем это должно случиться
   достаточно быстро ~ 10^-9
   с).

Несмотря
на отмеченные противоречия, определение
радиуса орбиты электрона и его энергии
на этой орбите ведется методом классической
физики.

Рассмотрим
электрон, движущийся в поле атомного
ядра с зарядом Ze.
При Z=1
такая система соответствует атому
водорода, при других Z
– водородопо­добному иону, т. е. атому
с порядковым номером Z,
из которого удалены все электроны, кроме
одного. Уравнение движения электрона
имеет вид:

(5)

Исключив
скорость V
из уравнений (3) и (5), получим выражения
для радиусов допустимых орбит:

(n=1,
2, 3…). (6)

Радиус
первой орбиты электрона в атоме водорода
называется боровским радиусом (его
принято обозначать символом r₀
или а₀
вместо r₁):

.

Полная
энергия электрона в водородоподобной
системе складывается из его кинетической
энергии (ядро считаем неподвижным) и
потенциальной энергии электрона в поле
ядра:

.
(7)

Из
(5) следует, что

Следовательно,

Подставив сюда выражение (6) для радиуса
n-ой
орбиты электрона r_n,
найдем допустимые значения внутренней
энергии атома в состоянии с главным
квантовым числом n
(n=1,
2, 3…):

(7)

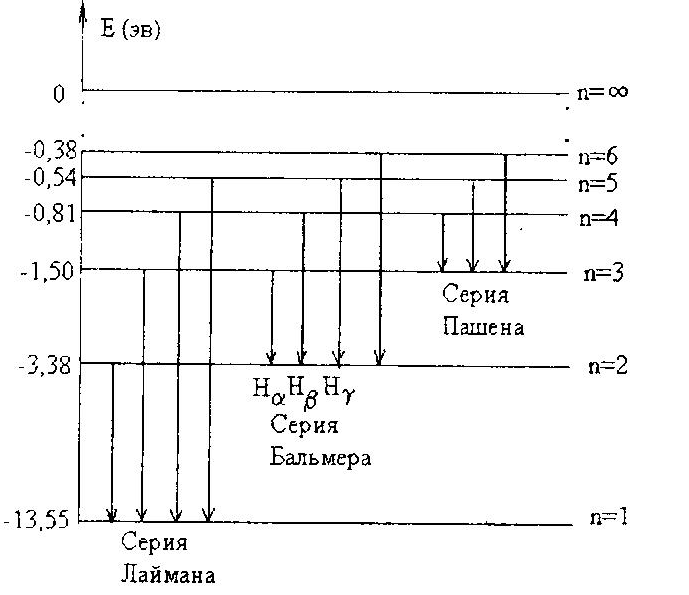
Зависимость
энергии атома водорода от квантового
числа n
можно показать на диаграмме энергетических
уровней, где по одной из осей отложены
значения энергии Е_n
(рис. 1).

Рис. 1

Состояние с n=1 соответствует наименьшей возможной энергии (Е1= -13,55эВ) и является основным (нормальным) состоянием. Все остальные состояния с n>1являются возбужденными. Максимуму энергии соответствует n=∞ (Е∞= 0). Это состояние соответствует ионизации атома, т.е. отрыву от него электрона.

Изменения
энергии электрона при переходе между
состояниями могут быть символически
изображены на той же диаграмме стрелками,
проведенными из начального состояния
в конечное.

Все
линии спектра излучения, относящиеся
к переходам на один и тот же уровень,
образуют серию. Так, если электрон
переходит из возбужденных состояний
на основной уровень, получаем серию
Лаймана. Линии, соответствующие переходам
на уровень с главным квантовым числом
n= 2, об­разуют серию Бальмера. Первые
три линии этой серии принято обозначать
так: Н_α
– красная, H_β
– зеленая, Н_γ
– фиолетовая. Это переходы с 3, 4, 5 уровней,
соответстственно. (В спектрах поглощения
серия определяется значением главного
квантового числа состояния, с которого
происходит переход на более возбужденный
уровень).

Согласно
второму постулату Бора:

₍₉₎

_{где
R–
постоянная Ридберга. Разделив на
постоянную Планка h,
получаем обобщенную формулу Бальмера
для частоты излучения при переходе
электрона из состояния с главным
квантовым числом n
в состояние
с m.}

Планетарная
теория атома приводит к очень хорошим
результатам в случае атома водорода и
сходных с ним ионов (в частности, она
дает точное значение постоянной
Ридберга), однако, для других атомов она
не работает. Этот успех явился для Бора
и других теоретиков мощным толчком к
развитию квантовой теории атома.

Способность
атомов и молекул поглощать и испускать
электромагнитное излучение используется
в спектральных методах анализа, которые
позволяют быстро и точно установить
состав вещества. Например, спектральные
методы применяются при контроле сырья,
промежуточных продуктов, готовой
продук­ции в различных технологических
процессах. Спектральные методы анализа,
благодаря своей высокой чувствительности,
позволяют определить малые кон­центрации
(следы) соединений в чистых и сверхчистых
веществах. Поэтому они широко применяются
при изготовлении полупроводников,
материалов атомной и электронной
промышленности, при решении задач охраны
природы и окружающей среды и в других
областях науки и техники.

Описание
установки

Для
изучения спектров используются различные
спектральные приборы, основной частью
которых являются монохроматоры. Они
выделяют из спектра сложного излучения
узкие спектральные участки, т.е. дают
свет практически одной и той же длины
волны (монохроматический свет).
Принципиальная схема монохроматора
показана на рис. 2.

Рис.
2

Свет
от источ­ника 1 падает на узкую щель
2, которая помещается в фокальной
плоскости линзы 3. Щель 2 и линза 3 образуют
коллиматор, т.е. оптическое устройство,
дающее параллельные пучки света. Далее
они падают на трехгранную призму 4
(обычно в монохроматорах используются
комбинации призм). Из-за дисперсии –
зависимости показателя преломления
вещества (стекла призмы) от длины волны
электромагнитного излучения – лучи
разных длин волн преломляются неодинаково.
Поэтому параллельные световые пучки,
соответствующие различным длинам волн,
оставаясь параллельными, будут идти
после призмы под различными углами друг
к другу (на рис. 2 показаны только два
пучка). На пути этих световых лучей стоит
линза 5, в фокальной плоскости которой
помещен экран 6. Если источник излучает
несколько определенных длин волн, то
на экране получается соответствующее
количество линий на некоторых расстояниях
друг от друга (линейчатый спектр). Если
же спектр источника сплошной, то на
экране образуется окрашенная полоса.

В
центре поля зрения находится указатель,
с которым совмещаются спектральные
линии. Если поворачивать призму 4 вокруг
оси, перпендикулярной плоскости рисунка,
то спектр в поле зрения будет смещаться.
Таким образом, можно просмотреть весь
спектр излучения.

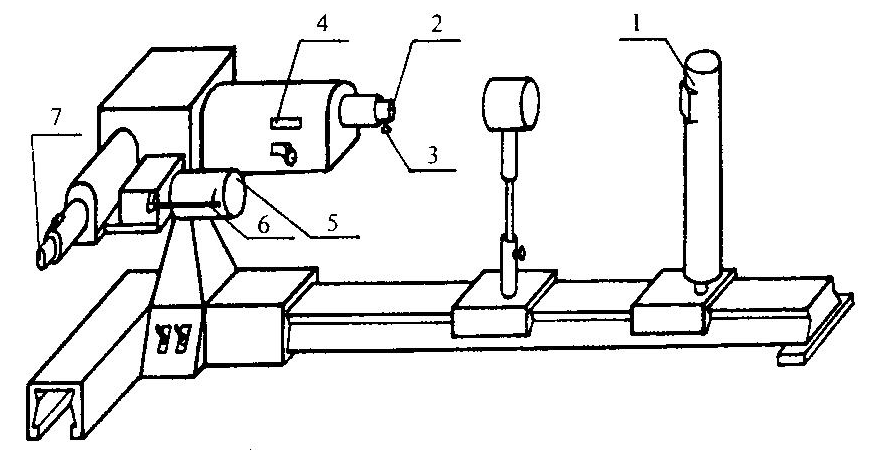
Рис.
3

На
рис. 3 представлена установка, которая
состоит из лампы 1 и монохроматора УМ-2.
Свет от источника 1 (ртутная или водородная
лампа) падает на входную щель коллиматора,
ширина которой может регулироваться
микровинтом 3. Поворот призмы осуществляется
с помощью барабана 5 с указателем 6. При
повороте барабана указатель 6 скользит
по спиральной канавке, на которую
нанесены деления в градусах. Ввиду того,
что фокусное расстояние объектива для
каждой длины волны изменяется,
предусмотрена фокусировка объектива.
В корпусе коллиматора имеется окошко
с миллиметровой шкалой и нониусом 4.
Фокусировка объектива производится
вращением маховичка 2.

Лучи
света, пройдя диспергирующую призму,
попадают в объектив трубы монохроматора,
который собирает их в фокусе окуляра.
На конце зрительной трубы находится
накатанное кольцо 7 для получения резкого
изображения указателя и спектральных
линий.

Чтобы
использовать монохроматор для изучения
спектров, необходимо его проградуировать,
т.е. поставить длины волн эталонных
спектральных линий в соответствие
делениям на барабане. В качестве
эталонного спектра в работе используется
спектр ртути, состоящий из большого
числа ярких линий, длины волн которых
тщательно измерены заранее.

Порядок
выполнения работы

Задание1.
Градуировка
монохроматора

1. Перед
   щелью монохроматора установить ртутную
   лампу и включить ее (не более чем на 5-7
   минут; включение лампы следует производить
   только под наблюдением лаборанта).

2. Перемещением
   окуляра зрительной трубы и объектива
   коллиматора добить­ся резкого
   изображения в поле зрения указателя и
   спектральных линий лам­пы. Ширина
   входной щели объектива должна быть
   достаточно узкой для то­го, чтобы
   линии были хорошо разрешены.

3. В
   зрительную трубу прибора рассмотреть
   спектр. Вращением барабана добиться
   совпадения стрелки указателя
   последовательно с теми линиями спектра,
   для которых приведены длины волн на
   рис. 4 и в табл. 1. Положение каждой линии
   определяется по показаниям на шкале
   барабана и записывается в табл. 1. Следует
   помнить, что ртутная лампа зажигается
   только в холодном состоянии, поэтому,
   прежде чем погасить ее, покажите
   результаты преподавателю.

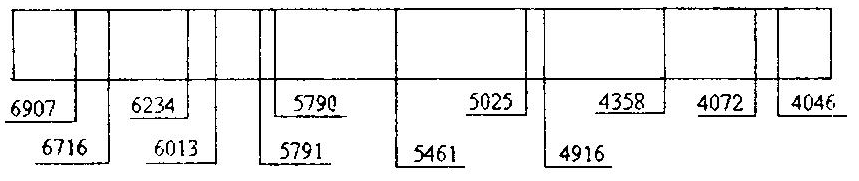
Рис.
4

1. Построить
   градуировочный график монохроматора.
   Для этого по оси абсцисс отложить
   деления барабана, по оси ординат –
   соответствующие длины волн в Ангстремах
   (1А⁰
   =
   10^-10м).
   За начало координат при этом удобно
   взять λ=4000 А⁰
   и соответствующее этой длине волны
   показание барабана. Критерием правильности
   построения графика является его
   плавность и от­сутствие изломов и
   перегибов.

Таблица
1

Источник излучения	Цвет линии	Показания барабана монохроматора	Длина волны, А0
Ртуть	Темно-красная яркая		6907
Темно-красная слабая		6716
Красная яркая		6234
Красная слабая		6073
Интенсивный желтый дублет		5791 5790
Зеленая яркая		5461
Сине-зеленая слабая		5026
Голубая яркая		4916
Темно-синяя яркая		4358
Фиолетовая яркая		4078
Фиолетовая яркая		4046

Задание
2. Измерение
длин волн линий в спектре излучения
водорода

1. Используя
   построенный по спектру ртути градуировочный
   график монохроматора, получить длины
   волн в спектре излучения водорода (в
   А⁰).
   Данные занести в табл. 2.

Таблица
2

Источник излучения	Цвет линии	Показания барабана монохроматора	Длина волны, А0
Водород

1. Рассчитать
   теоретические значения длин волн
   излучения водорода в видимой части
   спектра по формуле Бальмера по формуле
   (2) для красной, зеленой и фиолетовой
   линий.

2. Сравнить
   результаты расчетов и измерений.

Контрольные
вопросы

1. Что
   называют спектром излучения? Какие
   спектры бывают?

2. Как
   устроена модель атома Резерфорда?

3. Сформулируйте
   постулаты Бора. Каким положениям
   классической теории они противоречат?

4. Рассчитайте
   радиус орбиты электрона и энергию
   электрона на орбите.

5. Объясните
   смысл отрицательного значения энергии
   электрона в атоме.

6. Запишите
   формулу Бальмера для частоты спектральных
   линий атома водорода. Как связаны
   частота и длина волны электромагнитного
   излучения?

7. Перечислите
   серии спектра водорода. Какому переходу
   электрона соответствует головная линия
   (начало) каждой серии?

8. Чем
   определяется граница (конец) каждой
   серии? Почему к границе серии интенсивность
   линий уменьшается?

9. Каким
   переходам электронов соответствуют
   самые интенсивные линии видимой части
   спектра водорода?

10. Каков
    физический смысл квантовых чисел?

11. На
    каком явлении основан принцип действия
    монохроматора? Лучи какой длины волны
    преломляются призмой сильнее?

12. Что
    значит проградуировать монохроматор?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

А́том водоро́да — физико-химическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра, как правило, входит протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон образует электронную оболочку; наибольшая вероятность обнаружения электрона в единичном объёме наблюдается для центра атома. Интегрирование по сферическому слою показывает, что наибольшая вероятность обнаружения электрона в единичном слое соответствует среднему радиусу, равному боровскому радиусу ангстрема.

Атом водорода имеет особое значение в квантовой механике и релятивистской квантовой механике, поскольку для него задача двух тел имеет точное или приближённое аналитическое решение. Эти решения применимы для разных изотопов водорода (с соответствующими поправками).

В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощённо рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.

В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.

Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантовомеханическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.

Решение уравнения Шрёдингера[править | править код]

Решение уравнения Шрёдингера для водородного атома использует тот факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следует полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.

В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/r радиальные волновые функции записываются с использованием полиномов Лагерра. Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.

Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство — особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).

Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода — проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и полученных для другой выделенной оси всегда представляется как подходящая суперпозиция различных состояний с разными m (но тем же самым l), которые были получены для Z.

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид где e — заряд электрона (и протона), r — радиус-вектор, то уравнение Шрёдингера запишется следующим образом:

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона,  — постоянная Планка, E — полная энергия электрона,  — оператор Лапласа.
Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно будет записать лапласиан в сферической системе координат В ней он выглядит следующим образом:

Уравнение Шрёдингера в сферических координатах:

В этом уравнении  — функция трёх переменных Разделим его на три более простых уравнения. Для этого представим функцию как произведение трёх функций: Эти функции будем обозначать просто Тогда:

После подстановки значений частных производных в уравнение Шрёдингера получим:

Умножим уравнение на

Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.

Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её Следовательно:

Решением этого уравнения являются функции:

Угол φ может изменяться от 0 до 2π. Функция должна быть периодической с периодом 2π. Это возможно, только если Таким образом, из решения уравнения Шрёдингера получаем значение одного из квантовых чисел (конечно, из него можно получить их все). Число называется магнитным квантовым числом.

Далее, интегрируя квадрат модуля функции от 0 до 2π и приравнивая полученное выражение к единице, получим, что

Далее рассмотрим левую часть уравнения (1). Она, конечно, равна

Разделим уравнение на

После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через получаем:

Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.

Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален Число n называется главным квантовым числом. Оно может иметь значения от 1 до Его связь с энергией см. ниже.

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).

Магнитное квантовое число определяет проекцию орбитального момента количества движения на выбранную ось в магнитном поле. Эта проекция равна

Математическое описание атома водорода[править | править код]

Энергетический спектр[править | править код]

Энергетические уровни атома водорода, включая подуровни тонкой структуры, записываются в виде:

где  — постоянная тонкой структуры,

 — собственное значение оператора полного момента импульса.

Энергию можно найти в простой модели Бора, с массой электрона и зарядом электрона e:

(в системе СИ),

где h — постоянная Планка, электрическая постоянная. Величина E₀ (энергия связи атома водорода в основном состоянии) равна 13,62323824 эВ = 2,182700518⋅10⁻¹⁸ Дж. Эти значения несколько отличаются от действительного значения E₀, поскольку в расчёте не учтена конечная масса ядра и эффекты квантовой электродинамики.

Волновые функции[править | править код]

В сферических координатах волновые функции имеют вид:

где:  — Боровский радиус,

 — обобщённые полиномы Лагерра степени от функции

 — нормированные на единицу сферические функции.

Угловой момент[править | править код]

Собственные значения для оператора углового момента:

Нахождение энергии электрона из модели Бора[править | править код]

Вычислим уровни энергии атома водорода без учёта тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения центростремительной силе получим:

Здесь масса электрона, его скорость на орбите радиуса диэлектрическая проницаемость вакуума (электрическая постоянная).

Отсюда кинетическая энергия электрона:

где расстояние от электрона до ядра.

Потенциальная его энергия:

Полная энергия, соответственно, равна:

Для нахождения радиуса r_n стационарной орбиты с номером n рассмотрим систему уравнений, в которой второе уравнение есть математическое выражение первого постулата Бора

Отсюда получаем выражение для радиуса стационарной орбиты с номером n:

Радиус первой орбиты оказывается равным метра. Эта константа называется боровским радиусом.

Подставляя это значение в выражение для энергии, получим:

Отсюда мы можем найти волновое число (по определению это обратная длина волны или число длин волн, укладывающихся на 1 см) фотона, излучаемого атомом водорода за один переход из возбуждённого состояния с главным квантовым числом в состояние с неким фиксированным главным квантовым числом

где постоянная Ридберга в системе СГС (она равна 109 737,31568539 см⁻¹)^[1].

Визуализация орбиталей атома водорода[править | править код]

Изображение справа показывает первые несколько орбиталей атома водорода (собственные функции гамильтониана). Они представляют собой поперечные сечения плотности вероятности, величина которой отражена цветом (чёрный цвет соответствует минимальной плотности вероятности а белый — максимальной). Квантовое число углового момента l обозначено в каждой колонке, используя обычные спектроскопические обозначения (s означает l = 0; p: l = 1; d: l = 2). Главное квантовое число n (= 1, 2, 3…) отмечено справа от каждого ряда. Для всех картин магнитное квантовое число m равно 0, и сечение взято в плоскости — XZ, Z — вертикальная ось. Плотность вероятности в трёхмерном пространстве получается при вращении картинки вокруг оси Z.

Основное состояние, то есть состояние самой низкой энергии, в котором обычно находится электрон, является первым, состоянием 1s (n = 1, l = 0). Изображение с большим количеством орбиталей доступно до более высоких чисел n и l. Отметим наличие чёрных линий, которые появляются на каждой картинке, за исключением первой. Они — узловые линии (которые являются фактически узловыми поверхностями в трёх измерениях). Их общее количество всегда равно n − 1, которое является суммой числа радиальных узлов (равного n − l − 1) и числа угловых узлов (равного l).

Строение и свойства атома водорода[править | править код]

Образование атома водорода и его спектр излучения[править | править код]

При попадании в электрическое поле положительно заряженного протона и отрицательно заряженного электрона происходит захват последнего протоном — образуется атом водорода. Образовавшийся атом водорода находится в возбуждённом состоянии. Время жизни атома водорода в возбуждённом состоянии — доли или единицы наносекунд (10⁻⁸—10⁻¹⁰сек)^[2], однако очень высоковозбуждённые атомы, находящиеся в состоянии с большими главными квантовыми числами при отсутствии столкновений с другими частицами, в очень разрежённых газах могут существовать до нескольких секунд. Снятие возбуждения атома происходит за счёт излучения фотонов с фиксированной энергией, проявляющихся в характерном спектре излучения водорода. Поскольку объём газообразного атомарного водорода содержит множество атомов в различных состояниях возбуждения, спектр состоит из большого числа линий.

Схема образования спектра атомарного водорода и спектральные серии представлена на рисунке^[3].

Линии спектра серии Лаймана обусловлены переходом электронов на нижний уровень с квантовым числом n = 1 с уровней с квантовыми числами n = 2, 3, 4, 5, 6… Линии Лаймана лежат в ультрафиолетовой области спектра. Линии спектра серии Бальмера обусловлены переходом электронов на уровень с квантовым числом n = 2 с уровней с квантовыми числами n = 3, 4, 5, 6… и лежат в видимой области спектра.

Линии спектра серий Пашена, Брэкета и Пфунда обусловлены переходом электронов на уровни с квантовыми числами n, равными 3, 4 и 5 (соответственно), и расположены в инфракрасной области спектра^[4].

В нормальном (основном) состоянии (главное квантовое число n = 1) атом водорода в изолированном виде может существовать неограниченное время. Согласно квантовохимическим расчётам, радиус места наибольшей вероятности нахождения электрона в атоме водорода в нормальном состоянии (главное квантовое число n = 1) равен 0,529 Å. Этот радиус является одной из основных атомных констант, он получил название боровский радиус (см. выше). При возбуждении атома водорода электрон проходит на более высокий квантовый уровень (главное квантовое число n = 2, 3, 4 и т. д.), при этом радиус места наибольшей вероятности нахождения электрона в атоме возрастает пропорционально квадрату главного квантового числа:

r_n = a₀ · n².

Возбуждение и ионизация атома водорода[править | править код]

Возбуждение атома водорода происходит при нагревании, электроразряде, поглощении света и т. д., причём в любом случае атом водорода поглощает определённые порции — кванты энергии, соответствующие разности энергетических уровней электронов. Обратный переход электрона сопровождается выделением точно такой же порции энергии. Квантовые переходы электрона соответствуют скачкообразному изменению концентрического шарового слоя вокруг ядра атома водорода, в котором преимущественно находится электрон (шаровым слой является только при нулевом значении азимутального квантового числа l).

Согласно квантовомеханическим расчётам, наиболее вероятное расстояние электрона от ядра в атоме водорода равно боровскому радиусу ~ 0,53 Å при n = 1; 2,12 Å — при n = 2; 4,77 Å — при n = 3 и так далее. Значения этих радиусов относятся как квадраты натуральных чисел (главного квантового числа) 1² : 2² : 3²…. В очень разреженных средах (например, в межзвёздной среде) наблюдаются атомы водорода с главными квантовыми числами до 1000 (ридберговские атомы), чьи радиусы достигают сотых долей миллиметра.

Если электрону в основном состоянии придать дополнительную энергию, превышающую энергию связи E₀ ≈ 13,6 эВ, происходит ионизация атома водорода — распад атома на протон и электрон.

Строение атома водорода в основном состоянии[править | править код]

Радиальная зависимость dp(r)/dr плотности вероятности нахождения электрона в атоме водорода, находящемся в основном состоянии, представлена на рисунке. Эта зависимость даёт вероятность того, что электрон будет обнаружен в тонком шаровом слое радиуса r толщиной dr с центром в ядре. Площадь этого слоя равна S = 4πr², его объём dV = 4πr²dr. Общая вероятность нахождения электрона в слое равна (4πr²dr) ψ², поскольку в основном состоянии волновая функция электрона сферически симметрична (то есть постоянна в рассматриваемом шаровом слое). Рисунок выражает зависимость dp(r)/dr = 4πr²ψ². Кривая радиального распределения плотности вероятности dp(r)/dr нахождения электрона в атоме водорода имеет максимум при a₀. Этот наиболее вероятный радиус совпадает с боровским радиусом. Размытое облако плотности вероятности, полученное при квантовомеханическом рассмотрении, значительно отличается от результатов теории Бора и согласуется с принципом неопределённости Гейзенберга. Это размытое сферически симметричное распределение плотности вероятности нахождения электрона, называемое электронной оболочкой, экранирует ядро и делает физическую систему протон-электрон электронейтральной и сферически симметричной — у атома водорода в основном состоянии отсутствуют электрический и магнитный дипольные моменты (как и моменты более высоких порядков), если пренебречь спинами электрона и ядра. Максимум объёмной плотности вероятности ψ² достигается не при r = a₀, как для радиальной зависимости, а при r = 0.

Атом водорода в электрическом поле[править | править код]

По теории деформационной поляризации, нейтральный атом водорода, попадая во внешнее электрическое поле, подвергается деформации — центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L, что приводит к появлению в атоме водорода наведённого электрического дипольного момента μ^[5]. Величина наведённого дипольного момента прямо пропорциональна напряжённости внешнего электрического поля E:

μ = α_eE = Lq

Коэффициент пропорциональности α_e носит название электронной поляризуемости. Электронная поляризуемость атома водорода составляет 0,66 ų.^[6]

Чем выше напряжённость приложенного электрического поля, тем больше смещение центра электронной оболочки от центра атома водорода и, собственно, длина наведённого диполя:

L = α_e E/q,

где q — величина заряда ядра атома водорода.

При высоких значениях напряжённости приложенного электрического поля атом водорода подвергается ионизации полем с образованием свободных протона и электрона.

Взаимодействие атома водорода с протоном[править | править код]

Протон, обладая положительным элементарным электрическим зарядом q = 1,602•10 ⁻¹⁹ Кл, как и всякий точечный электрический заряд создаёт вокруг себя электрическое поле с напряжённостью E.
E = q/R²,
Где R — расстояние точки поля до протона.

Нейтральный атом водорода, попадая в электрическое поле протона, подвергается деформационной поляризации (см. рисунок). Длина наведённого электрического диполя атома водорода обратно пропорциональна квадрату расстояния между атомом водорода и протоном L = α_e E/q = α_e/R² = 0,66/R²

Отрицательный полюс наведённого электрического диполя атома водорода ориентируется в сторону протона. В результате чего начинает проявляться электростатическое притяжение между атомом водорода и протоном. Сближение частиц (атома водорода и протона) возможно до тех пор, пока центр плотности вероятности нахождения электрона станет равноудалённым от обоих протонов. В этом предельном случае d=R=2L. Центр области вероятного нахождения электрона совпадает с центром симметрии образовавшейся системы H₂⁺ — молекулярного иона водорода, при этом
d=R=2L=³√2α_e = ³√2•0,66 = 1,097 Å.

Найденная величина d = 1,097 Å близка к экспериментальной величине межъядерного расстояния в молекулярном ионе водорода H₂⁺ — 1,06 Å.^[7]

Взаимодействуя с протоном, атом водорода образует молекулярный ион водорода

H₂⁺,H + H ⁺ -> H₂⁺ + Q,

Характеризующийся простейшей одноэлектронной ковалентной химической связью.

Взаимодействие атома водорода с электроном[править | править код]

Электрон, обладая элементарным электрическим зарядом, как и протон, создаёт вокруг себя электрическое поле, но (в отличие от электрического поля протона) с отрицательным знаком. Нейтральный атом водорода, попадая в электрическое поле электрона, подвергается деформационной поляризации. Центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L в противоположную сторону к приближающемуся электрону. Приближающийся электрон как бы вытесняет из атома водорода находящийся в нём электрон, подготавливая место для второго электрона. Величина смещения центра электронной оболочки атома водорода L обратно пропорциональна квадрату расстояния атома водорода к приближающемуся электрону R:

L = α_e/R² = 0.66/R² (рис)

Сближение атома водорода и электрона возможно до тех пор, пока центры областей плотностей вероятности нахождения обоих электронов не станут равноудалёнными от ядра объединённой системы — отрицательно заряженного иона водорода. Такое состояние системы имеет место при

r_e = L = R = ³√0,66 = 0,871 Å,

где r_e — орбитальный радиус двухэлектронной оболочки гидрид-иона H^–.

Таким образом, атом водорода проявляет своеобразную амфотерность: он может взаимодействовать как с положительно заряженной частицей (протоном), образуя молекулярный ион водорода H₂⁺, так и с отрицательно заряженной частицей (электроном), образуя гидрид-ион H^–.

Рекомбинация атомов водорода[править | править код]

Рекомбинация атомов водорода обсуловлена силами межатомного взаимодействия. Происхождение сил, вызывающих притяжение электрически нейтральных атомов друг к другу, было объяснено в 1930 году Ф.Лондоном. Межатомное притяжение возникает вследствие флуктуации электрических зарядов в двух атомах, находящихся близко друг от друга. Поскольку электроны в атомах движутся, то каждый атом обладает мгновенным электрическим дипольным моментом, отличным от нуля. Мгновенный диполь на одном атоме наводит противоположно направленный диполь в соседнем атоме. Наступает синхронизация колебаний двух атомов — двух осцилляторов, частоты которых совпадают. Результатом этого процесса является образование молекулы водорода.

Наличие мгновенного электрического дипольного момента у атома водорода выражается в характерной особенности атома водорода, проявляющейся в крайней реакционной способности атомарного водорода и склонности его к рекомбинации. Время существования атомарного водорода составляет около 1 с при давлении в 0,2 мм рт. ст. Рекомбинация атомов водорода имеет место, если образующаяся молекула водорода быстро освобождается от избытка энергии, выделяющейся при взаимодействии атомов водорода путём тройного столкновения. Соединение атомов водорода в молекулу протекает значительно быстрее на поверхности различных металлов, чем в самом газе. При этом металл воспринимает ту энергию, которая выделяется при образовании молекул водорода, и нагревается до очень высоких температур. Тепловой эффект реакции образования молекулярного водорода из атомов водорода составляет 103 ккал/моль.

На принципе рекомбинации атомов водорода разработана атомно-водородная сварка. Между двумя вольфрамовыми стержнями создаётся электрическая дуга, через которую по облегающим стержни трубкам пропускается ток водорода. При этом часть молекул водорода распадается на атомы, которые затем вновь соединяются на металлической поверхности, помещаемой на небольшом расстоянии от дуги. Металл может быть таким путём нагрет до температуры выше 3500° C^[8].

Константы реакции диссоциации молекулярного водорода (K_p) и степень превращения водорода в атомарное состояние (α) в зависимости от абсолютной температуры (T) представлены в таблице^[9]:

T, к	2000	3000	4000	5000	6000	8000
Кр	2,62 · 10-6	2,47 · 10-2	2,52	4,09 · 10	2,62 · 102	2,70 · 103
α	8,10 · 10-4	7,83 · 10-2	0,621	0,954	0,992	0,999

См. также[править | править код]

• Водород
• Водородоподобный атом
• Квантовая механика
• Квантовая химия
• Квантовая теория поля
• Квантовое состояние
• Принцип неопределённости
• Волновая функция
• Электронное облако
• Ридберговский атом

Примечания[править | править код]

Литература[править | править код]

• Luca Nanni. The Hydrogen Atom: a Review on the Birth of Modern Quantum Mechanics (англ.). — arXiv:1501.05894.

Ссылки[править | править код]

• Griffiths  (англ.) (рус., David J. Introduction to Quantum Mechanics (англ.). — Upper Saddle River, NJ: Prentice Hall, 1995.
• Bransden, B.H.; C.J. Joachain. Physics of Atoms and Molecules (англ.). — London: Longman, 1983.
• Физика атома водорода на Scienceworld
• Графическое представление орбиталей
• Апплет, изображающий орбитали атома водорода