Скорость
света в среде
равна
![]()
где
с
– скорость света в вакууме; n
– показатель преломления среды.
Оптическая
длина пути
световой волны определяется по формуле
![]()
,
где
l
– геометрическая длина пути луча в
среде с показателем преломления n.
Оптическая
разность хода
двух лучей равна
![]()
.
Оптическая
разность хода
![]()
световых волн, отраженных от верхней и
нижней поверхностей тонкой плоскопараллельной
пластинки или пленки с показателем
преломления n,
находящейся в воздухе, равна
![]()
,
где
d
– толщина пластинки (пленки);
– угол падения;
![]()
– длина волны света.
Связь
разности фаз
![]()
с оптической разностью хода
имеет вид
![]()
,
где
– длина световой волны.
Условие
максимумов
интенсивности света при интерференции
имеет вид
![]()
,
где
k
= 0,1,2,3,…
Условие
минимумов
интенсивности света при интерференции
имеет вид
![]()
,
где
k
= 0,1,2,3,…
Радиусы
светлых колец
Ньютона в
отраженном свете (или темных в проходящем)
равны
![]()
,
где
k
– номер кольца (k
= 1, 2, 3,…); R
– радиус кривизны линзы.
Радиус
темных колец
Ньютона в
отраженном свете (или светлых в проходящем)
равны
![]()
.
Задачи
19.1.
Сколько
длин волн монохроматического света с
частотой колебаний
ν = 5·1014
Гц уложится на пути длиной l
= 1,2 мм:
1) в вакууме;
2) в стекле?
19.2.
Определить длину l1
отрезка, на котором укладывается столько
же длин волн в вакууме, сколько их
укладывается на отрезке
l2
= 3 мм в воде.
19.3.
Какой длины l1
путь пройдет фронт волны монохроматического
света в вакууме за то же время, за какое
он проходит путь длиной
l2
= 1 м в воде?
19.4.
На пути световой волны, идущей в воздухе,
поставили стеклянную
пластинку толщиной h
= 1 мм.
На сколько изменится оптическая
длина пути, если волна падает на пластинку:
1) нормально;
2) под углом
![]()
= 300?
19.5.
На пути монохроматического света с
длиной волны
=
0,6 мкм находится плоскопараллельная
стеклянная пластина
толщиной
d
= 0,l
мм. Свет падает на пластину
нормально. На какой угол
следует повернуть пластину, чтобы
оптическая
длина пути L
изменилась
на
![]()
?
19.6.
Оптическая разность хода
двух интерферирующих волн монохроматического
света равна 0,3λ. Определить разность
фаз
.
19.7.
Найти все длины волн видимого света (от
0,76 до 0,38мкм), которые
будут: 1) максимально усилены; 2) максимально
ослаблены при
оптической разности хода
интерферирующих волн, равной 1,8
мкм.
19.8.
Расстояние d
между
двумя когерентными источниками света
(
= 0,5 мкм) в опыте Юнга равно 0,1 мм. Расстояние
b
между
интерференционными
полосами на экране в средней части
интерференционной картины равно 1
см. Определить расстояние l
от источников до экрана.
19.9.
Расстояние
d
между
двумя щелями в опыте Юнга равно
1
мм, расстояние l
от щелей до экрана равно 3 м. Определить
длину
волны
,
испускаемой источником монохроматического
света, если ширина
b
полос
интерференции на экране равна 1,5 мм.
19.10.
Плоская световая волна падает на
бизеркала Френеля, угол
между которыми φ = 2′. Определить длину
волны света, если
ширина интерференционной полосы на
экране Δх
= 0,55 мм.
19.11.
Плоская
онохроматическая световая
волна падает нормально на диафрагму
с двумя узкими щелями, отстоящими друг
от друга на
d
= 2,5мм.
На
экране, расположенном за диафрагмой на
l=
100
см, образуется система интерференционных
полос. На какое
расстояние и в какую сторону сместятся
эти полосы, если одну
из щелей перекрыть стеклянной пластинкой
толщины h
= 10
мкм?
19.12.
Плоскопараллельная
стеклянная
пластинка толщиной d
=
1,2 мкм и показателем преломления n
= 1,5 помещена между двумя средами
с показателями преломления n1
и
п2.
Свет с длиной волны
= 0,6
мкм падает нормально на пластинку.
Определить оптическую разность
хода
волн, отраженных
от
верхней и нижней поверхностей пластинки,
и указать, усиление или ослабление
интенсивности света происходит при
интерференции
в следующих случаях: 1) n1<n<n2;
2) n1>n>n2;
3) п1<п>п2;4)
n1>n<n2.
19.13.
На
мыльную пленку (n
= 1,3), находящуюся в воздухе, падает
нормально пучок лучей белого света. При
какой наименьшей толщине
d
пленки
отраженный свет с длиной волны λ= 0,55
мкм окажется
максимально усиленным в результате
интерференции?
19.14.
Пучок монохроматических (λ= 0,б мкм)
световых волн падает
под углом
= 30° на находящуюся в воздухе мыльную
пленку
(n
= 1,3). При какой наименьшей толщине d
пленки
отраженные световые волны будут: 1)
максимально ослаблены интерференцией;
2) максимально
усилены интерференцией?
19.15.
Найти минимальную толщину пленки с
показателем преломления
1,33, при которой свет с длиной волны 0,64
мкм испытывает
максимальное отражение, а свет с длиной
волны 0,4
мкм не отражается совсем. Угол падения
света равен 300.
19.16.
На тонкий стеклянный клин (n
= 1,55), находящийся в воздухе, падает
нормально монохроматический
свет. Двугранный угол α между поверхностями
клина равен 2/.
Определить длину световой волны λ, если
расстояние
b
между
соседними интерференционными максимумами
в отраженном
свете равно 0,3 мм.
19.17.
Поверхности стеклянного клина образуют
между собой угол
θ = 0,2/.
На клин нормально к его поверхности
падает пучок лучей
монохроматического света с длиной волны
= 0,55 мкм. Определить
ширину b
интерференционной
полосы.
19.18.
Между
двумя плоскопараллельными стеклянными
пластинками положили очень тонкую
проволочку, расположенную параллельно
линии соприкосновения пластинок и
находящуюся на
расстоянии l
= 75 мм от нее. В отраженном свете (
= 0,5 мкм) на верхней
пластинке видны интерференционные
полосы. Определить диаметр
d
поперечного
сечения проволочки, если на протяжении
а
=
30 мм насчитывается т
=16
светлых
полос.
19.19.
Две плоскопараллельные стеклянные
пластинки образуют клин
с углом θ = 30//.
Пространство между пластинками заполнено
глицерином.
На клин нормально к его поверхности
падает пучок монохроматического
света с длиной волны λ = 500 нм. В отраженном
свете наблюдается интерференционная
картина. Какое число N
темных
интерференционных полос приходится на
1 см длины клина?
19.20.
Расстояние между вторым и первым темным
кольцами
Ньютона в отраженном свете равно 1 мм.
Определить расстояние
между десятым и девятым кольцами.
19.21
.Плосковыпуклая
линза выпуклой стороной лежит на
стеклянной
пластинке. Определить толщину d
слоя
воздуха там, где
в отраженном свете (λ= 0,6 мкм) видно первое
светлое кольцо Ньютона.
19.22.
Диаметр
d2
второго
светлого кольца Ньютона при наблюдении
в отраженном свете (λ= 0,6 мкм) равен 1,2
мм.
Определить
оптическую силу D
плосковыпуклой стеклянной линзы, взятой
для опыта.
19.23.
Плосковыпуклая линза с оптической силой
D
= 2 дптр
выпуклой стороной лежит на
стеклянной пластинке. Радиус
четвертого
темного кольца Ньютона в проходящем
свете равен
0,7 мм. Определить длину
световой волны.
19.24.
Диаметры di
и dk
двух светлых колец Ньютона соответственно
равны 4,0 мм и 4,8 мм. Порядковые номера
колец не определялись, но известно,
что между двумя измеренными кольцами
расположено три светлых кольца.
Кольца наблюдались в отраженном свете
(λ= 500 нм). Найти радиус кривизны
плосковыпуклой линзы, взятой для
опыта.
19.25.
Между стеклянной пластинкой и лежащей
на ней плосковыпуклой стеклянной
линзой налита жидкость, показатель
преломления которой меньше показателя
преломления стекла. Радиус восьмого
темного кольца Ньютона при наблюдении
в отраженном свете (λ= 700 нм) равен 2 мм.
Радиус R
кривизны выпуклой поверхности линзы
равен 1 м. Найти показатель преломления
n
жидкости.
19.26.
На установке для наблюдения колец
Ньютона был измерен в отраженном свете
радиус третьего темного кольца (k
= 3). Когда пространство между
плоскопараллельной пластиной и линзой
заполнили жидкостью, то тот же радиус
стало иметь кольцо с номером, на единицу
большим. Определить показатель
преломления n
жидкости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Интерференция света:
Фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Монохроматической волной называется электромагнитное излучение постоянной частоты.
Рассмотрим процесс наложения волн длиной 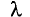
Монохроматические волны одной и той же частоты, приходящие от этих источников в некоторую точку пространства Р, возбуждают в ней гармонические колебания той же частоты.
В силу этого, разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке Р, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.
Волны называются когерентными, если разность фаз колебаний, возбуждаемых ими, не изменяется с течением времени. Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью (от латинского слова cohaerens — связанный, сцепленный).
Опыт показывает, что амплитуда результирующего колебания в точке Р, создаваемого двумя одинаковыми источниками, зависит от геометрической разности хода волн до рассматриваемой точки:

Если разность хода волн 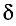 равна целому числу длин волн
равна целому числу длин волн 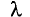 (четному числу полуволн
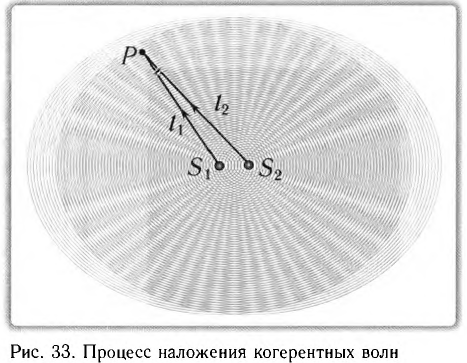
(четному числу полуволн 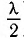 ) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
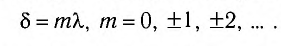
Действительно, разность фаз колебаний в рассматриваемой точке в этом случае
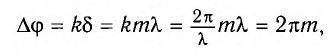
т. е. кратна 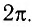 .
.
В случае, когда разность хода волн равна нечетному числу полуволн, волны приходят в точку Р в противофазе и ослабляют друг друга. Это соответствует выполнению условия минимума:
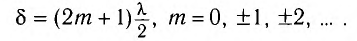
Убедитесь самостоятельно, что разность фаз колебаний в этом случае
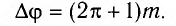
Таким образом, в результате сложения колебаний, возбуждаемых когерентными волнами на поверхности воды, образуется устойчивая картина распределения минимумов и максимумов результирующего колебания (рис. 34). Это означает, что когерентные волны интерферируют друг с другом.

Интерференция (от латинских слов inter — взаимно, между собой и fеrio — ударяю, поражаю) — явление сложения двух или более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания.
Пространственная картина устойчивого во времени распределения амплитуд результирующего колебания при интерференции называется интерференционной картиной.
Вследствие того, что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания в общем случае не равна сумме энергий складываемых колебаний, так как 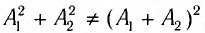 . Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
. Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.
Закономерности интерференции волн носят универсальный характер, т. е. справедливы для волн любой природы.
При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Это эквивалентно замене геометрической разности хода на оптическую разность хода
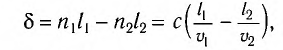
т. е. разность расстояний, пройденных волнами, с учетом различных скоростей 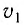 и
и 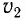 их распространения в средах с показателями преломления
их распространения в средах с показателями преломления 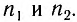
В вакууме (с = 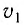 =
=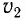 ) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
Распространенные бытовые источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.
Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
Для получения интерференционной картины при отсутствии лазеров пользуются классической интерференционной схемой (схемой Юнга), где пучок света разделяется на два пучка с помощью отверстий В и С в ширме (рис. 35). Поскольку эти пучки созданы одним и тем же источником, они являются когерентными. На экране в области DE наблюдается интерференционная картина.
Классический эксперимент по наблюдению интерференции Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.
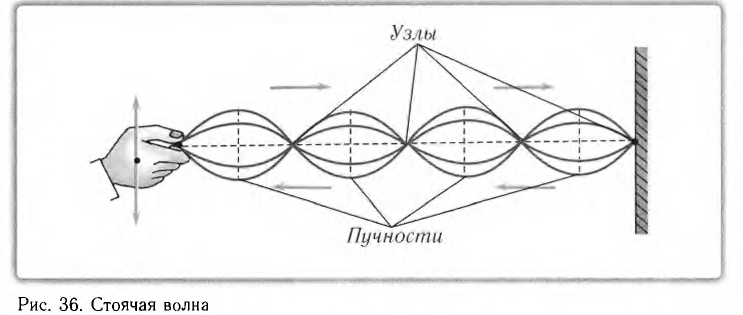
Рассмотрим еще один распространенный случай интерференции — сложение волн с одинаковыми частотами, распространяющихся в противоположных направлениях (например, падающей и отраженной волны), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов).
Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 36).
Пример решения задачи:
Рассчитайте положения максимумов и минимумов интерференционной картины на экране MN, находящемся на расстоянии L = АО = 2,0 м от двух одинаковых когерентных источников света 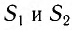 , которые расположены в вакууме на расстоянии
, которые расположены в вакууме на расстоянии 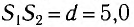 мм друг от друга (рис. 37). Длина волны излучения источников
мм друг от друга (рис. 37). Длина волны излучения источников 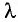 = 600 нм. Найдите расстояние
= 600 нм. Найдите расстояние 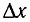 между соседними максимумами.
между соседними максимумами.
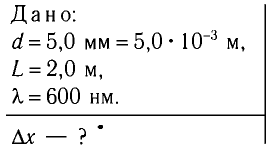
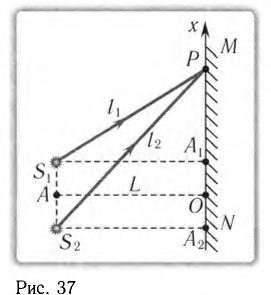
Решение
До некоторой точки Р на экране волны проходят пути 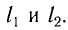
Максимумы интенсивности будут наблюдаться при условии
а минимумы при условии – 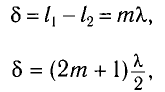
где m = 0, ±1, ±2…..
По теореме Пифагора из треугольников 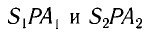 находим
находим
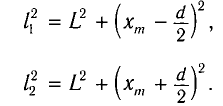
Откуда
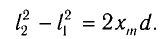
С учетом того, что 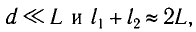 находим
находим
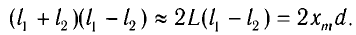
С учетом условия максимумов получаем
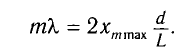
Откуда расстояние от центра экрана до т-й светлой полосы находится из соотношения
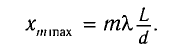
Из условия минимумов находим положение темных полос:
Откуда 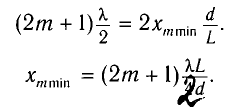
Расстояние между соседними максимумами 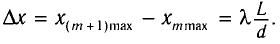
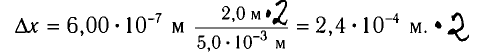
Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния d между когерентными источниками.
Ответ: 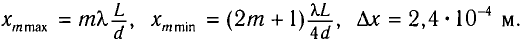
Волновая природа света и дисперсия света
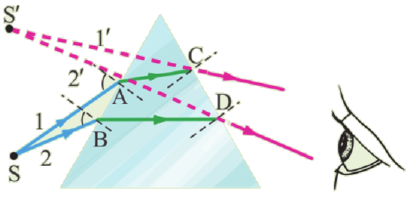
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше скорости света в вакууме:
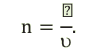
Луч света, падающий на боковую грань треугольной призмы, отклоняется к основанию призмы.
Природа света
Несколько веков имели место два разных представления о природе света: корпускулярная и волновая природа света.
Основоположником представлений о корпускулярной природе света является И. Ньютон. Он считал, что свет является потоком частиц (корпускул). Прямолинейное распространение света и его отражение легко объяснялись согласно этому представлению.
Основоположником представлений о волновой природе света является голландский ученый Христиан Гюйгенс (1629-1695). Основной причиной возникновения этих представлений является прохождение световых лучей сквозь друг друга при распространении подобно волнам. В XIX веке английский ученый Томас Юнг (1773-1829) провел эксперименты, в которых обнаружил многочисленные факты, подтверждающие волновую природу света. Основоположник теории электромагнитного поля Дж. Максвелл теоретически обосновал электромагнитную волновую природу света. Согласно современным представлениям свет и другие электромагнитные волны обладают двойной – корпускулярной и волновой природой.
- Заказать решение задач по физике
Дисперсия света
Одним из явлений, доказывающих волновую природу света, является дисперсия света.
Дисперсия света — это зависимость показателя преломления среды от частоты (длины волны) падающего света.
Впервые это явление исследовал Исаак Ньютон. Он поместил прозрачную стеклянную треугольную призму на пути тонкого пучка солнечного света, попадающего в затемненную комнату через маленькое отверстие в ставнях. Пройдя призму, солнечный луч разделился на спектр из семи составных цветных лучей. Последовательность цветов составных частей в дисперсионном спектре всегда одинакова: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Среди монохроматических (содержащих свет одного цвета) лучей наиболее сильно преломляются фиолетовые лучи, а меньше других – красные (см: а). Причина явления объясняется на основе волновых представлений о свете. Так, абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше, чем в вакууме:

Здесь 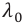 – длина световой волны в вакууме.
– длина световой волны в вакууме. 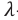 – длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от
– длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от 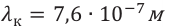 (красный) до
(красный) до 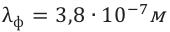 (фиолетовый).
(фиолетовый).
Результат. Таким образом, явление дисперсии показало, что белый свет обладает сложным строением – состоит из монохроматических световых лучей разного цвета. Каждый монохроматический луч света обладает собственной частотой и длиной волны. Поэтому при прохождении монохроматического луча через стеклянную призму он, только преломляясь, изменяет своё направление (не разлагается на составные, не меняет окраски). Если разложенный призмой свет, состоящий из монохроматических составляющих, направить на вторую перевернутую призму, то на выходе из второй призмы опять получится белый свет.
Согласно физике цвета, ни один из трех основных цветов – красный, зеленый и синий, не могут получиться при смешивании двух других. Однако смешиванием основных цветов можно получить все остальные цвета и их оттенки.
Многоцветное восприятие нами окружающего мира объясняется явлениями поглощения, преломления и отражения света. Например, лист бумаги воспринимается нашим зрением белым потому, что он отражает падающий на него белый свет полностью. Если тело полностью поглощает падающий на него свет, то он воспринимается как черный, например, сажа.
Интерференция волн и интерференция света
• Самые часто встречаемые колебания в природе являются колебаниями в связанных системах. В связанных колебательных системах колебания передаются от одного звена системы другой. Например, бросив в воду камень, можно наблюдать распространение концентрических водных кругов из точки падения камня. Нам кажется, что происходит распространение воды в виде выпуклостей и впадин.
Какая связанная система создает волну в воде?
Какие явления происходят в среде при распространении волны?
Обратите внимание на картину, образованную на неподвижной поверхности воды поплавками удочек рыболовов (а). При встрече волн друг с другом происходит их сложение. В результате в определенных точках пространства они усиливают друг друга (а, 1), а в других ослабляют (а, 2).

Интерференция волн
В исследовании вы наблюдали результат сложения когерентных волн, созданных на поверхности воды гармоническими колебаниями шариков генератора с одинаковой частотой.
Когерентные волны — это волны, созданные различными источниками колебания, имеющими одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.
Результирующие колебания, образованные сложением когерентных волн, в зависимости от разности между расстояниями от источника колебаний до точки их встречи или усиливаются, или ослабляются – происходит интерференция волн.
Интерференция волн -усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. “интер” взаимно, “ферио” – ударю).
Усиление или ослабление амплитуды результирующей волны определяется условиями максимума и минимума интерференции.
Условие максимума интерференции
Максимум интерференции наблюдается в точках пространства (поверхности), в которых максимумы слагаемых волн накладываются друг на друга. Это зависит от разницы пройденных волнами путей от источника колебаний до этой точки.
Интерференционный максимум результирующей волны образуется в точках, в которых разность хода складываемых волн равна нулю или четному числу полудлин волн (разность фаз равна нулю или четному количеству 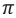 ) (d):
) (d):
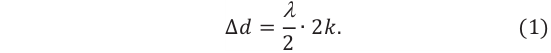
Здесь 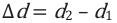 – разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
– разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
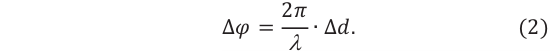
Учитывая выражение (1) в формуле (2), для разницы фаз максимума интерференции получим:
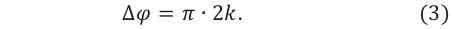
В этом случае при равенстве амплитуд складываемых волн амплитуда результирующего колебания будет равна сумме амплитуд исходных волн (е):
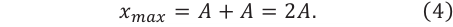
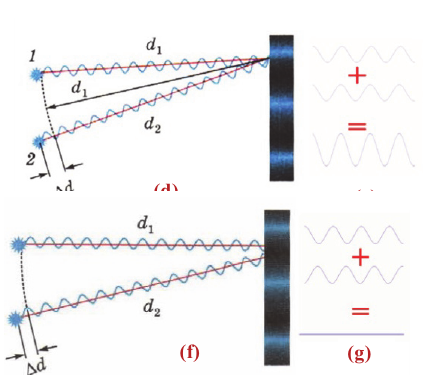
Условие минимума интерференции
Минимумы интерференции наблюдаются в тех точках пространства, в которые волны доходят в противофазе. При этом максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.
Минимум интерференции наблюдается в точках, в которых разность хода слагаемых волн равна нечетному числу полудлин волн (разность фаз равна нечетному количеству 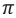 ) (f):
) (f):
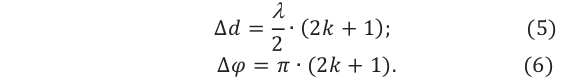
Если при этом амплитуды складываемых волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g):
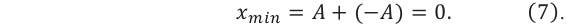
Интерференция света
Интерференция – характерное свойство всех видов волн, в том числе и световых. Так, две световые волны при сложении в пространстве могут усиливать или ослаблять друг друга, даже может случиться и такой вариант: свет + свет = темнота.
Интерференция света – явление увеличения или уменьшения амплитуды результирующих световых колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
Долгие годы не могли найти способ получения когерентных световых волн, поэтому невозможно было доказать способность световых волн интерферировать.
Только в начале XIX века с помощью несложного устройства Томас Юнг смог наблюдать интерференцию света (h).
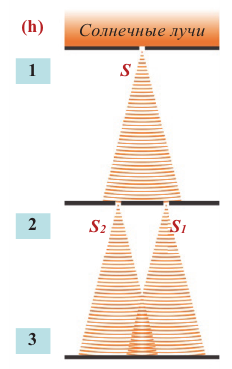

Классический опыт по наблюдению интерференции света состоит в следующем: солнечный свет освещает непрозрачный экран 1 и, пройдя через малое отверстие S в этом экране (проделанное булавкой), попадает на экран 2. Световые лучи, вышедшие из малых отверстий S1 и S2 на втором экране, являются когерентными. В результате интерференции этих волн на экране 3 появляются интерференционные полосы. В центральной части экрана наблюдаются чередующиеся цветные и темные полосы. По мере удаления от центра интерференционная картина ослабевает. Используя условие максимумов в этих опытах, Юнг смог на основе формулы (1) измерить длины световых волн для разных цветов. Как ни странно, первый опыт по интерференции света был проведен отрицающим его волновую природу Исааком Ньютоном. Поместив на стеклянной пластине плоско-выпуклую стеклянную линзу выпуклой стороной вниз, он осветил её сверху (i, 1). Посмотрев на линзу сверху, Ньютон увидел чередующиеся светлые и темные концентрические круги (i, 2), которые впоследствии стали называть кольцами Ньютона. Но ни Ньютон, ни повторявшие этот интересный опыт в течение более чем 100 лет ученые не смогли объяснить причину возникновения этих колец. И только в 1802 году Юнгу удалось объяснить происхождение колец Ньютона. Он объяснил кольца Ньютона таким образом: когда пучок света падает на плоскую поверхность линзы, то он, проходя сквозь нее, частично отражается от нижней сферической поверхности линзы (см. i-З, луч 1), а частично – от поверхности стеклянной пластинки, на которой лежит линза (см. i-З, луч 2). Вследствие такого многократного отражения образуются два когерентных луча. Эти лучи, складываясь, в соответствии с максимумами и минимумами интерференции создают интерференционную картину чередующихся темных и светлых концентрических кольца.
Определение длины световой волны
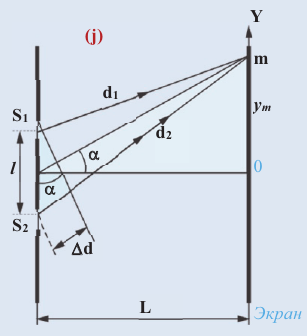
Представим, что расстояние между источниками когерентных волн S1 и S2 намного меньше расстояния от источников до экрана (j):  В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой
В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой 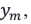 , можно считать параллельными. Разность хода между этими лучами:
, можно считать параллельными. Разность хода между этими лучами:
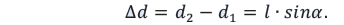
Вследствие малости угла 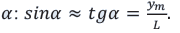
Условие интерференционного максимума в этом случае будет:

Отсюда можно найти длину волны:

- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
- Преломление света
- Полное отражение
- Дисперсия света
- Электромагнитная природа света
Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.
Интерференция механических волн
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.

Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.
Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O1 и O2 (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.
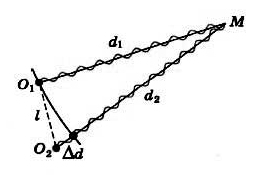
Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода, определяемую формулой:
Δd = d2 − d1
Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Δd=(2k+1)λ2
k = 0, 1, 2, … .
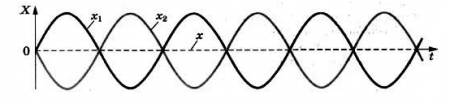
Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.
Δd=kλ
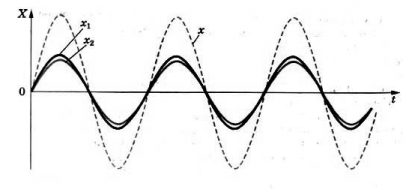
Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.

Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.
Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.
Распределение энергии при интерференции
Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.
Интерференция света
Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.
Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.

Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.
Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:
Δd=kλ
Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:
Δd=(2k+1)λ2
Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.
Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.
Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.
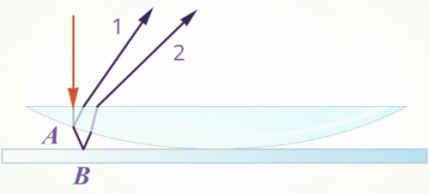
Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.
В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)
Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.
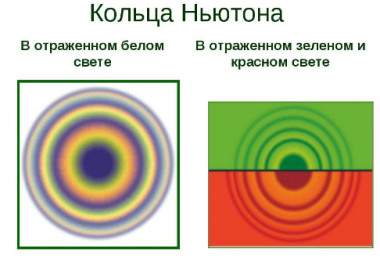
Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λкр = 8∙10–7 м, а для фиолетового — λa = 4∙ 10–7 м.
Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?
Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет вид чередующихся цветных и темных полос. Цвет полос определяется цветом световой волны, который зависит от ее длины волны.
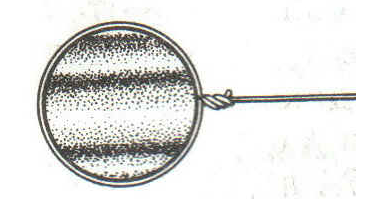
Задание EF17533
На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет
Ответ:
а) только зелёной
б) находиться ближе к красной области спектра
в) находиться ближе к синей области спектра
г) только полностью чёрной
Алгоритм решения
1.Описать наблюдаемое явление.
2.Записать условие наблюдения интерференционного максимума.
3.Выполнить решение в общем виде.
4.Установить, в какой цвет будет окрашена пленка.
Решение
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от передней и задней поверхностей плёнки. Условием интерференционного максимума для излучения с длиной волны λ является:
kλ=2dn+Δ
Δ — либо 0, либо λ2 (это зависит от соотношения показателей преломления на границе двуз сред). Тогда при малом изменении значения показателя преломления в меньшую сторону и сохранении порядка k (как в нашем случае и есть), длина волны света будет уменьшаться. Это значит, что из зеленой части спектра она сдвинется в синюю часть.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17707
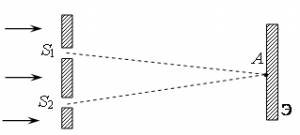 На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если
На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если
Ответ:
а) S2А – S1А = 2k⋅λ/2, где k– любое целое число
б) S2А – S1А = (2k + 1) ⋅λ/2, где k– любое целое число
в) S2А – S1А = λ/3k, где k– любое целое число
г) S2А – S1А = λ/(2k+1), где k– любое целое число
Алгоритм решения
1.Записать условие наблюдения интерференционного минимума.
2.Выбрать выражение, удовлетворяющее этому условию.
Решение
В точке А будет наблюдаться темное пятно, если волны, достигающие этой точки, будут гасить друг друга. Это возможно при соблюдении условия минимума:
Δd=(2k+1)λ2
Разность хода в данном случае равна:
Δd=S2A−S1A
Следовательно:
S2A−S1A=(2k+1)λ2
где k — целое число.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17972
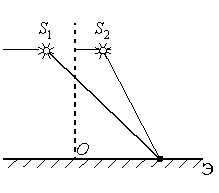 Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые
Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые
Ответ:
а) каждое своей лампочкой накаливания
б) каждое своей горящей свечой
в) одно зелёным лазером, другое красным
г) светом одной лампочки накаливания
Алгоритм решения
- Записать условие наблюдения интерференционной картины.
- Проанализировать источники и выбрать подходящий под условие.
Решение
Четкая интерференционная картина наблюдается только при освещении щелей когерентными лучами света, имеющими постоянную разность фаз. Когерентные — значит волнами одной частоты. Поэтому лазер зеленый и красный сразу не подходят — они имеют разные частоты.
Одна и та же частота и постоянная разность фаз будет только при условии, что щели освещаются одним источником света. В данном случае — одной и той же лампой накаливания.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.6k
Интерференция
- Подробности
- Категория: Оптика
Необходимы более веские доказательства того, что свет при распространении ведет себя как волна. Любому волновому движению присущи явления интерференции и дифракции. Для того чтобы быть уверенным в том, что свет имеет волновую природу, необходимо найти экспериментальные доказательства интерференции и дифракции света.
Интерференция — достаточно сложное явление . Чтобы лучше понять его суть, мы вначале остановимся на интерференции механических волн.
Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?
Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.
Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.
Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.
Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.
Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.

Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, который совершает гармонические колебания (рис. 118). В любой точке М на поверхности воды (рис. 119) будут складываться колебания, вызванные двумя волнами (от источников O1 и О2). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, отличаться, так как волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей (l « d1 и l « d2 ) , то обе амплитуды
можно считать практически одинаковыми.
Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода Δd = d2—d1. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

Условие максимумов. На рисунке 120 изображена зависимость от времени смещений X1 и X2 , вызванных двумя волнами при Δd= λ. Разность фаз колебаний равна нулю (или, что то же самое, 2л, так как период синуса равен 2п). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. Колебания результирующего смещения на рисунке показаны цветом (пунктир). То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.
Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:
Δd=κλ
где к=0,1,2,….

Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.
Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:
Δd=(2к+1)λ/2

Если разность хода d2 — d1 принимает промежуточное значение
между λ и λ/2 , то и амплитуда результирующего колебания принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но наиболее важно то, что Амплитуда колебаний в любой точке he меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 122 показан рисунок с фотографии интерференционной картины двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.
Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.
Источники, удовлетворяющие этим условиям, называются когерентными. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.
Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться. Поэтому амплитуда результирующих колебаний с течением времени изменяется. В результате максимумы и минимумы перемещаются в пространстве и интерференционная картина размывается.

Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы и в минимумах интерференционной картины выделяется тепло? Ничего подобного. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает совсем.
ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН
Если свет представляет собой поток волн, то должно наблюдаться явление интерференции света. Однако получить интерференционную картину (чередование максимумов и минимумов освещенности) с помощью двух независимых источников света, например двух электрических лампочек, невозможно. Включение еще одной лампочки лишь увеличивает освещенность поверхности, но не создает чередования минимумов и максимумов освещенности.
Выясним, в чем причина этого и при каких условиях можно наблюдать интерференцию света.
Условие когерентности световых волн. Причина состоит в том, что световые волны, излучаемые различными источниками, не согласованы друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковые длины волн и постоянную разность фаз в любой точке пространства. Напомним, что такие согласованные волны с одинаковыми длинами волн и постоянной разностью фаз называются когерентными.
Почти точного равенства длин волн от двух источников добиться нетрудно. Для этого достаточно использовать хорошие светофильтры, пропускающие свет в очень узком интервале длин волн. Но невозможно осуществить Постоянство разности фаз от двух независимых источников. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн, имеющими длину около метра. И такие цуги волн от обоих источников налагаются друг на друга. В результате амплитуда колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги волн от различных источников сдвинуты друг относительно друга по фазе. Волны от различных источников света некогерентны из-за того, что разность фаз волн не остается постоянной. Никакой устойчивой картины с определенным распределением максимумов и минимумов освещенности в пространстве не наблюдается.
Интерференция в тонких пленках. Тем не менее интерференцию света удается наблюдать. Курьез состоит в том, что ее наблюдали очень давно, но только не отдавали себе в этом отчета.
Вы тоже много раз видели интерференционную картину, когда в детстве развлекались пусканием мыльных пузырей или наблюдали за радужным переливом цветов тонкой пленки керосина или нефти на поверхности воды. «Мыльный пузырь, витая в воздухе… зажигается всеми оттенками цветов, присущими окружающим предметам. Мыльный пузырь, пожалуй, самое изысканное чудо природы» (Марк Твен). Именно интерференция света делает мыльный пузырь столь достойным восхищения.

Английский ученый Томас Юнг первым пришел к гениальной мысли о возможности объяснения цветов тонких пленок сложением волн 1 и 2 (рис. 123), одна из которых (1) отражается от наружной поверхности пленки, а вторая (2) —от внутренней. При этом происходит интерференция световых волн — сложение двух волн, вследствие которого наблюдается устойчивая во времени картина усиления или ослабления результирующих световых колебаний в различных точках пространства. Результат интерференции (усиление или ослабление результирующих колебаний) зависит от угла падения света на пленку, ее толщины и длины волны. Усиление света произойдет в том случае, если преломленная волна 2 отстанет от отраженной волны 1 на целое число длин волн. Если же вторая волна отстанет от первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света.

Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, обеспечивается тем, что они являются частями одного и того же светового пучка. Цуг волн от каждого излучающего атома разделяется пленкой на два, а затем эти части сводятся вместе и интерферируют.
Юнг также понял, что различие в цвете связано с различием в длине волны (или частоте световых волн). Световым пучкам различного цвета соответствуют волны различной длины. Для взаимного усиления волн, отличающихся друг от друга длиной (углы падения предполагаются одинаковыми), требуется различная толщина пленки. Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом должны появиться различные цвета.
Кольца Ньютона. Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.
Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса (рис.111). Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус . Все это вы можете проверить с помощью самостоятельных наблюдений.

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу (рис. 124). Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.
Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив радиусы колец, можно вычислить длины волн.
Длина световой волны. Для красного света измерения дают λкр = 8•10-7 м, а для фиолетового — λф = 4•10-7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.
Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.
Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10-6 см) разница в длине световых волн. Интересно, что большинство животных неспособны различать цвета. Они всегда видят чернобелую картину. Не различают цвета также дальтоники — люди, страдающие цветовой слепотой.
При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.
Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в n раз. Так как v = λv, то при этом должна уменьшиться в n раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в n раз именно длина волны, а не частота.
Интерференция электромагнитных волн. На опытах с генератором СВЧ можно наблюдать интерференцию электромагнитных (радио) волн.
Генератор и приемник располагают друг против друга (рис. 125). Затем подводят снизу металлическую пластину в горизонтальном положении. Постепенно поднимая пластину, обнаруживают поочередное ослабление и усиление звука.
Явление объясняется следующим образом. Часть волны из рупора генератора непосредственно попадает в приемный рупор. Другая же ее часть отражается от металлической пластины. Меняя расположение пластины, мы изменяем разность хода прямой и отраженной волн. Вследствие этого волны либо усиливают, либо ослабляют друг друга в зависимости от того, равна ли разность хода целому числу длин волн или нечетному числу полуволн.

Наблюдение интерференции света доказывает, что свет при распространении обнаруживает волновые свойства. Интерференционные опыты позволяют измерить длину световой волны: она очень мала—от 4•10-7 до 8•10-7 м.
Интерференция двух волн. Бипризма Френеля – 1
Интерференция двух волн. Бипризма Френеля – 2
Интерферометр Маха-Цандера: его устройство
Интерферометр Маха-Цандера. Поворот стеклянной пластинки
Интерферометр Маха-Цандера. «Деформация» основания»
Стоячие трехсантиметровые волны
Трехсантиметровые волны: стоячие волны в резонаторе
Дециметровая стоячая волна
«Стоячая волна» на экране осциллографа
Поперечные стоячие волны на линейке со свободным концом
Поперечные стоячие волны на резиновом шнуре
Поперечные стоячие волны на проводе с переменным током
Настройщик фортепиано и другие
Поющая Труба
Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.
Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.
В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).
Для математического описания явления интерференции вводят оптическую длину пути () — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):
(1)
- где

Рис. 1. Интерференция
Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( и
). Пути лучей в этих системах
и
соответственно. Затем, вышедшие из областей, лучи обратно свели в точку
. За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).
Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:
- максимум интерференции (максимальное усиление):
(2)
(3)
Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):
(4)
Тогда, если полученное целое или ближе к целому, то в точке
наблюдается усиление света, в случае, если
полуцелое или близко к полуцелому, в точке
— темнота.
Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).
Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства мкм. Каков будет результат интерференции в этой точке, если длина волны будет:
нм,
нм.
Исходя из аналитической формулы (4):
(5)
(6)
Таким образом, получившийся параметр получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр
оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.
