Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Опыт Юнга состоит в интерференции света от двух источников на экране. Когерентные источники в данном опыте получают путем разведения лучей от обычного источника света – сначала свет проходит через узкую щель S, дающую источник достаточно малого размера, затем он попадает на две узкие щели, расположенные симметрично, достаточно близко друг от друга – получаем когерентные источники S’ и S”. В области перекрывания волн от этих источников размещается экран, на котором наблюдается результат интерференции – чередование темных и светлых полос, то есть областей максимума и минимума интенсивностей света.
В опыте Юнга когерентные источники образованы отражением в зеркале источника, находящегося на расстоянии h от зеркала. Расстояние до экрана равно 1м. Первоначально ширина полос на экране равна 0,3 мм, после отодвигания источника от зеркала на дополнительное расстояние 0,6 мм ширина полос стала равной 0,2 мм. Найти длину волны света.
В опыте Юнга расстояние между щелями 0,1 мм, длина волны 0,6 мкм, ширина полос на экране 1 см. Найти расстояние от источников до экрана.
В опыте Юнга длина волны меняется с 500 нм на 650 нм. Во сколько раз изменилась ширина полос на экране?
В опыте Юнга расстояние между источника 1 мм, расстояние от источников до экрана 3м, ширина полос на экране 1,5 мм. Найти длину волн света.
В опыте Юнга расстояние между щелями 0,5 мм, длина волны 600 нм, расстояние от источников до экрана 3м. Найти ширину полос на экране.
В опыте Юнга расстояние между щелями 0,1 мм, длина волны 500 нм, расстояние от источников до экрана 1,2м. Найти ширину полос на экране.
В опыте Юнга расстояние между источника 0,5 мм, расстояние от источников до экрана 5м, ширина полос на экране 5 мм. Найти длину волн света.
В опыте Юнга расстояние между источника 0,7 мм, расстояние от источников до экрана 4м. Сколько светлых полос поместится на ширине экрана 2 см?
В опыте Юнга на ширине экрана 1 см размещается 10 темных полос. Расстояние до экрана 1 м. Найти расстояние между источниками.
Найти расстояние между красной и фиолетовой полосами второго порядка на экране в опыте Юнга.
В опыте Юнга на пути лучей от источников помещают две пластинки разной толщины. В какую сторону и на сколько сместятся полосы на экране?
Ниже вы можете посмотреть видеоролик, объясняющий смысл опыта Юнга.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.
При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.
Первый научный эксперимент проявления интерференции света
Первый научный эксперимент по наблюдению интерференции света провел в лабораторных условиях И. Ньютон. Ученый рассматривал интерференционную картину, которая возникала при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Наблюдение Ньютона графически изображено на рис. 3.7.1.
Интерференционная картина выглядела в виде концентрических колец, которые впоследствие получили название колец Ньютона (рис. 3.7.2).
Рисунок 3.7.1. Наблюдение колец Ньютона. Интерференционная картина возникает при сложении волн, отразившихся от 2-х сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн;
h – толщина воздушного зазора.
Рисунок 3.7.2. Кольца Ньютона в зеленом и красном свете.
У И. Ньютона не получилось с позиции корпускулярной теории дать объяснение тому, почему возникают кольца. Но ученый понимал, что это имеет отношение к какой-то периодичности световых процессов.
Интерференционный опыт Юнга
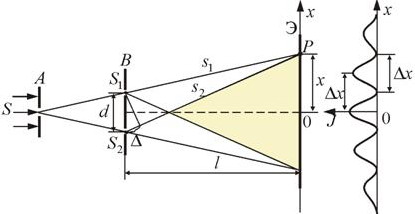
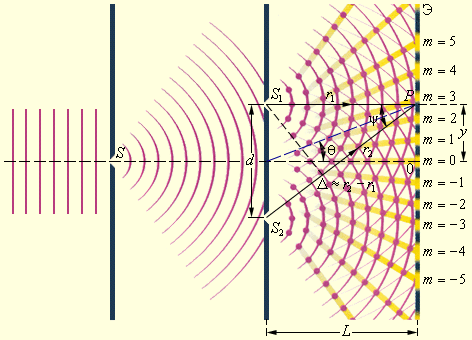
В 1802 году ученый Юнга провел первый интерференционный опыт, которому есть подтверждение в волновой теории света. В данном эксперименте свет от источника – узкой щели S попадал на экран с
2-мя близко расположенными друг к другу щелями S1 и S2, как показано на рис. 3.7.3. Минуя каждую из щелей, световой пучок уширялся из-за дифракции, а потому на белом экране Э световые пучки, которые прошли через щели S1 и S2, перекрывались. В месте перекрытия световых пучков находится интерференционная картина, выступающая в виде чередующихся светлых и темных полос.
Рисунок 3.7.3. Схема интерференционного опыта Юнга.
Ученый Юнг – первый, кто догадался, что невозможно увидеть интерференцию, если сложить волны от 2-х независимых источников. Потому в его эксперименте щели S1 и S2, которые по принципу Гюйгенса можно рассматривать в качестве источников вторичных волн, освещались светом одного источника S. Если симметрично расположить щели, то вторичные волны от источников S1 и S2 находятся в фазе, однако волны проходят до точки наблюдения P различные расстояния r1 и r2. Можно сделать вывод, что фазы колебаний, которые создаются волнами от источников S1 и S2 в точке P, различные. Следует, что задача об интерференции волн – это задача о сложении колебаний одинаковой частоты, но с различными фазами.
Высказывание о том, что волны от источников S1 и S2 распространяются независимым образом, а в точке наблюдения они складываются друг с другом, – это опытный факт, который называется принципом суперпозиции.
Монохроматическую (или синусоидальную) волну, распространяющуюся в направлении радиус-вектора r→, записывают в виде
E=a cos (ωt – kr),
где a – это амплитуда волны, k=2πλ – это волновое число, λ – это длина волны, ω=2πν – это круговая частота. При решении оптических задач под E предполагают модуль вектора напряженности электрического поля волны. При вкладывании 2-х волн в точке P итоговое колебание также случается на частоте ω и обладает некоторой амплитудой A и фазой φ:
E=a1·cos (ωt–kr1)+a2·cos (ωt – kr2)=A·cos (ωt-φ).
Приборы, которые могли бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существуют. Наблюдаемая величина – это поток энергии, прямо пропорциональный квадрату амплитуды электрического поля волны.
Физическая величина, равная квадрату амплитуды электрического поля волны, называется интенсивностью: I=A2.
Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P:
I=A2=a12+a22+2a1a2 cosk∆=I1+I2+2I1I2 cos k∆ (*),
где Δ=r2–r1 – это разность хода.
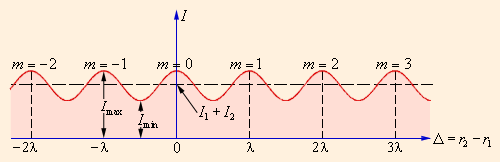
Из данного выражения можно сделать вывод, что интерференционный максимум (то есть светлая полоса) достигается в таких точках пространства, в которых Δ=mλ (m=0, ±1, ±2, …). Причем Imax=(a1+a2)2=I1+I2. Интерференционный минимум (то есть темная полоса) достигается при Δ=mλ+λ2. Минимальное значение интенсивности Imin=(a1–a2)2<I1+I2. Рис. 3.7.4 наглядно показывает, как распределяется интенсивность света в интерференционной картине, смотря от того, каким будет ход Δ.
Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – это порядок интерференционного максимума.
Предположим, что если I1=I2=I0, то есть длина 1 и 2 световой волны одинакова, то выражение (*) выглядит следующим образом:
I=2I0(1+cos kΔ) (**).
В данном случае Imax=4I0, Imin=0.
Формулы (*) и (**) – универсальные. Они подходят для любой интерференционной схемы, в которой складываются 2 монохроматические волны одинаковой частоты.
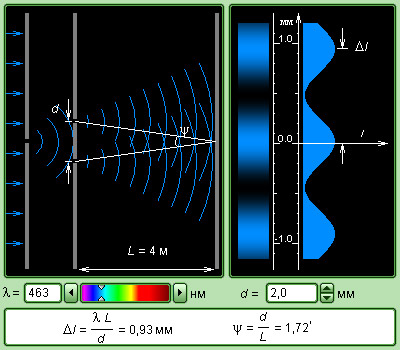
Обозначим в схеме Юнга смещение точки наблюдения от плоскости симметрии y, тогда в случае, когда d≪L и y≪L (как правило, в оптических экспериментах данные условия соблюдаются), можно приблизительно получить:
∆≈d·θ≈d·yL.
Разность хода Δ меняется на одну длину волны λ при смещении от одного интерференционного максимума к другому, то есть на расстояние, эквивалентное ширине интерференционной полосы Δl. Получается,
d·∆lL=λ или ∆l=L·λd≈λψ,
где ψ – это угол схождения «лучей» в точке наблюдения P.
Сделаем количественную оценку. Предположим, что расстояние d между 2-мя щелями S1 и S2 равняется 1 мм, а расстояние от щелей до экрана Э равно L=1 м, в таком случае ψ=dL=0,001 рад. Для света зеленого цвета (λ=500 нм) получаем Δl =λ ψ=5·105 нм=0,5 мм. Для света красного цвета (λ=600 нм) Δl=0,6 мм. Именно так Юнг в первый раз измерил длины световых волн, хоть и точность данных измерений была невысока.
Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.
Далее данный термин будет упоминаться без кавычек.
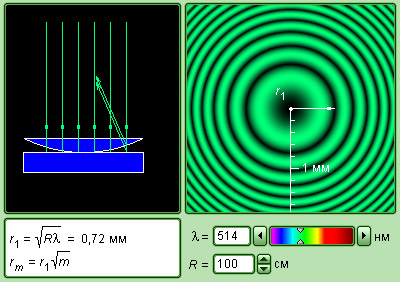
При рассмотрении эксперимента И. Ньютона (рис.3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода примерно равняется удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Если радиус кривизны R линзы огромен в сравнении с h, можно приблизительно получить формулу:
h≈r22R,
где r – это смещение от оси симметрии. Вычисляя разность хода, следует учитывать, что волны 1 и 2 отражаются при различных условиях. 1-я волна отражается от границы стекло–воздух, а 2-я – от границы воздух–стекло. В последнем варианте фаза колебаний отраженной волны изменяется на π, что равно увеличению разности хода на λ2. А потому
∆=2h+λ2≈r2R+λ2.
При условии r=0, то есть в центре (точка соприкосновения) Δ = λ2; потому в центре колец И. Ньютона всегда находится интерференционный минимум (зрительно это выглядит, как темное пятно). Радиусы rm следующих темных колец вычисляются по формуле
rm=mλR.
По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.
Проблема когерентности волн
С помощью теории Юнга объясняются интерференционные явления, которые возникают при сложении 2-х монохроматических волн одинаковой частоты. Но сегодняшний опыт показывает, что интерференцию света на самом деле наблюдать не так-то просто. Если комнату осветить 2 одинаковыми лампочками, то в любой точке сложатся интенсивности света и здесь не будет никакой интерференции. Тогда появляется вопрос, когда нужно сложить напряженности (учитывая фазовые соотношения), а когда – интенсивности волн, то есть квадраты напряженностей полей? К сожалению, теория интерференции монохроматических волн не дает ответ на данный вопрос.
Реальные световые волны – не строго монохроматические. По фундаментальным физическим причинам излучение всегда происходит статистически (или случайно). Атомы источника света излучают независимо друг от друга в какие-то моменты времени, и каждый атом излучает свет очень короткий промежуток времени (τ≤10–8 с). Итоговое излучение источника света в определенный момент времени складывается из вкладов огромного количества атомов. Спустя время порядка τ совокупность излучающих атомов полностью обновляется. Потому суммарное излучение будет с другой амплитудой и, что очень важно, с другой фазой. Фаза волны, которая излучается реальным источником света, примерно постоянна только лишь на интервалах времени порядка τ.
Отдельные «обрывки» излучения длительности τ называют цуги. Они обладают пространственной длиной, равной cτ, где c – это скорость света.
Колебания в различных цугах не согласованы друг с другом. Выходит, что реальная световая волна – это последовательность волновых цугов с беспорядочно меняющейся фазой. В физике принято считать, что колебания в различных цугах некогерентны. Временной интервал τ, в течение которого фаза колебаний примерно постоянна, называется временем когерентности.
Интерференция возникает только лишь при сложении когерентных колебаний, то есть колебаний, которые относятся к одному цугу. Хоть и фазы каждого колебания также подвергаются случайным временным изменениям, но данные изменения одинаковы, потому разность фаз когерентных колебаний постоянна. В данном случае наблюдается устойчивая интерференционная картина и, значит, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз – это случайная функция времени. В этом случае интерференционные полосы подвергаются беспорядочным перемещениям из одной стороны в другую, и за время Δt их регистрации, которая в оптических экспериментах существенно превышает время когерентности (Δt≫τ), наблюдается полное усреднение. Глаз, фотопластинка или фотоэлемент фиксирует в точке наблюдения усредненную величину интенсивности, равную сумме интенсивностей I1+I2 этих колебаний. Здесь соблюдается закон сложения интенсивностей.
Итак, интерференция возникает только лишь при сложении когерентных колебаний. Волны, которые создают в точке наблюдения когерентные колебания, тоже называют когерентными. Волны от 2-х независимых источников некогерентны и не дают интерференцию. Ученый Юнг интуитивно догадался для того, чтобы получить интерференцию света нужно волну от источника разделить на 2 когерентные волны и потом смотреть на экране результат их сложения. Так устроены все интерференционные схемы. Но даже в данном случае интерференционная картина пропадает, если разность хода Δ превышает длину когерентности cτ.
Рисунок 3.7.5. Модель кольца Ньютона.
Рисунок 3.7.6. Модель интерференционый опыт Юнга.
© www.phys.nsu.ru
5. Порядок выполнения работы
Работа включает в себя проведение двух опытов: по методу Юнга и с бипризмой Френеля.
Установите лабораторный источник света на оптической скамье (оптическом рельсе) и включите его блок питания (см. рис. 10). Включите полупроводниковый лазер и выставьте его с помощью регулировочных винтов так, чтобы его пучок распространялся строго вдоль оптической оси (в горизонтальной плоскости и вдоль скамьи). На расстоянии примерно 1 см за источником света поместите одиночную щель 2 (см. рис. 9) и установите ее ширину 0,1−0,2 мм. Введите в световой пучок двойную щель 3 и установите ее на расстоянии 6−8 см от щели 2. Располагая перед двойной щелью экран из белой бумаги (для контроля), добейтесь попадания пучка света на двойную щель. Установите в конце оптической ска-
мьи окуляр-микрометр МОВ 1 15 . Все элементы должны находиться на оптической оси установки.
Уменьшите ширину одиночной щели 2. Изменяя положение двойной щели (вдоль оптической оси) и устанавливая двойную щель параллельно щели 2 (слегка поворачивая оправу вокруг оптической оси), добейтесь появления ярких и широких интерференционных полос. Интерференционная картина рассматривается через окуляр 5. Меняя ширину одиночной щели 2, добейтесь наблюдения четких и достаточно ярких интерференционных полос.
Настройтесь на резкое изображение отсчетной шкалы (перекрестия) окуляр-микрометра. В поле зрения окулярного микрометра видны две пересекающиеся линии. Резкость перекрестия достигается вращением держателя линзы окулярного микрометра. С помощью окуляр-микрометра измерьте расстояние между светлыми (темными) интерференционными полосами. Для этого вращайте барабан окулярного микрометра и, перемещая перекрестие, определите, сколько делений микрометра укладывается между соответствующими интерференционными полосами. Цена наименьшего
33
© www.phys.nsu.ru
деления окулярного микрометра 0,001 мм. Измерения проведите между различными комбинациями полос. С помощью линейки измерьте расстояние между двойной щелью и плоскостью наблюдения интерференционной картины (соответствует метке на корпусе окуляр-микрометра 5).
Пользуясь формулой (31), вычислите длину волны излучения полупроводникового лазера. Определите среднее значение, оцените погрешность измерений. Для проверки надежности измерений полученное значение сравните с известной длиной волны лазера. Аналогичные измерения проведите для других квазимонохроматических источников света (красный, синий и зеленый светодиоды). Определите средние значения длин волн, оцените погрешности измерений.
Установите источник белого света. Обратите внимание на изменение вида интерференционной картины. Оцените среднюю длину волны в спектре излучения. Сравните со средним значением длины волны видимого света. Объясните различие в интерференционной картине по сравнению со случаем квазимонохроматического источника света.
Для одного из квазимонохроматических светодиодов исследуйте (качественно) влияние ширины одиночной щели 2 на видность (четкость) интерференционных полос. Плавно увеличивая ширину щели, добейтесь исчезновения интерференционной картины (видность равна нулю). Пользуясь соотношением (26), оцените максимальную ширину щели, при которой видность уменьшается до нуля. Сравните с экспериментальным значением, определенным по лимбу микрометрического винта щели 2. Объясните исчезновение интерференционной картины в случае увеличения ее ширины.
5.2. Определение длины волны света с помощью бипризмы Френеля
Длину волны света можно также определить с помощью формулы (4), если под d понимать расстояние между мнимыми источниками S1 и S2 (см. рис. 6). Однако методически выполнение задания упростится, если длину волны лазера считать заданной (λлаз = 0,655 мкм). Как видно из выражения (30), ширина полосы (расстояние между соседними, например, светлыми интерференцион-
34
© www.phys.nsu.ru
ными полосами) прямо пропорционально длине волны света (при сохранении геометрии опыта).
Включите полупроводниковый лазер и выставьте его с помощью регулировочных винтов так, чтобы его пучок распространялся строго вдоль оптической оси (в горизонтальной плоскости и вдоль скамьи). Введите в световой пучок бипризму Френеля 4 (см. рис. 9)
и установите ее на расстоянии 6 8 см от одиночной щели с плавно регулируемой шириной 2. На расстоянии 50 см от щели 2 после бипризмы установите окуляр-микрометр 5. Бипризма Френеля и окуляр-микрометр должны располагаться на оптической оси установки.
Перемещая бипризму немного вправо или влево и устанавливая ее ребра параллельно щели 2 (слегка поворачивая бипризму вокруг оптической оси), добейтесь появления ярких интерференционных полос. Перемещая бипризму Френеля и окуляр-микрометр вдоль оптической оси и меняя ширину щели 2, добейтесь наблюдения четких, достаточно ярких и широких интерференционных полос. Зафиксируйте положение бипризмы и окуляр-микрометра на опти-
ческой оси (при дальнейших измерениях их положение не меняет-
ся). Измерьте расстояние между светлыми (темными) интерференционными полосами с помощью окуляр-микрометра. Используйте различные комбинации полос. Найдите среднее значение ширины
полосы x( лаз)для лазерного источника света.
Поочередно устанавливая различные светодиодные источники света при сохранении геометрии опыта, найдите средние значения ширины интерференционных полос для каждого из них. Длину волны излучения светодиодов можно найти из соотношения для относительных величин
|
лаз |
x( лаз ) |
и |
лаз x( ) |
, |
(39) |
|
|
x( ) |
x( |
) |
||||
|
лаз |
где x( ) − среднее значение ширины полосы для соответствую-
щего светодиодного излучателя.
С помощью формулы (39) вычислите средние значения длин волн для различных светодиодных источников, оцените погрешности измерений.
35

© www.phys.nsu.ru
Обратите внимание на изменение интерференционной картины в случае источника белого света. Исследуйте также влияние ширины щели 2 на видность интерференционных полос.
Контрольные вопросы
1.Как влияет дифракция света на щелях S1, S2 в условиях реального эксперимента (см. рис. 5) на интенсивность интерференционной картины?
2.Почему при увеличении ширины (протяженности) первичного источника света S интерференционные полосы становятся менее четкими?
3.Какой вид имеют интерференционные полосы в плоскостях,
нормальных к S1S2, в опыте Меслина (половинки разрезанной линзы смещены вдоль оси)?
Приложение для физиков
Влияние ширины спектра источника света на видность интерференционной картины
Более строгий теоретический анализ влияния ширины спектра первичного источника требует учета спектрального распределения интенсивности в интерферирующих пучках. Предположим, что излучение точечного источника S (см. рис. 7) имеет непрерывный
спектр в интервале длин волн от 1 до 2 . В соответствии с выра-
жением (29) вклад в интенсивность излучения от каждой монохроматической компоненты в интервале d равен
|
cos( |
2 ndx |
(40) |
||
|
dI (xP , ) 2I 1 |
L |
P ) d , |
||
36

© www.phys.nsu.ru
где I − спектральное распределение интенсивности в каждом
пучке. Так как отдельные спектральные компоненты некогерентны, то полная интенсивность в точке наблюдения равна
|
2 |
2 ndx |
P |
|||||
|
I (xP ) 2 |
I 1 |
cos( |
) d . |
(41) |
|||
|
L |
|||||||
|
1 |
Пусть в качестве источника света S используется свечение газоразрядной плазмы низкого давления (например, излучение гелийнеонового лазера). В этом случае основной причиной уширения спектральной линии является хаотическое тепловое движение излучающих атомов (доплеровское уширение). Спектральное распределение интенсивности определяется выражением
|
I |
I |
exp( 4ln2 ( )2 |
/( )2 ), |
(42) |
||
|
0 |
||||||
|
0 |
где I 0 − спектральная интенсивность в центре линии ( 0 ), а
(2 0 /c) 2kT ln2/M
есть полуширина контура (расстояние между двумя точками, интенсивность в которых равна (1/2)I 0 ) [5]. В последней формуле k
− постоянная Больцмана; c − скорость света в вакууме; M − масса атома; T − абсолютная температура. Распределение (42) симметрично относительно 0 (кривая Гаусса).
В этом случае выражение для интенсивности (41) можно представить в виде
|
2 |
4ln2 ( )2 |
|||||||||
|
I (xP ) 2I 0 exp( |
( )2 |
0 |
)d |
|||||||
|
1 |
||||||||||
|
2 |
4ln2 ( )2 |
2 ndxp |
||||||||
|
2I 0 exp( |
( ) |
2 |
0 |
)cos( |
)d . |
(43) |
||||
|
L |
||||||||||
|
1 |
||||||||||
Спектральное распределение (42) отлично от нуля лишь в узком интервале длин волн вблизи центра линии излучения 0 . Если пе-
рейти в выражении (43) к новой переменной интегрирования
|
0 , |
можно пределы интегрирования по |
рассматривать |
|
от до |
для упрощения расчетов. Положив |
4ln2/( )2 , |
найдем, что первый член в выражении (2.16) сводится к интегралу Пуассона. Действительно,
37
© www.phys.nsu.ru
|
2I 0 |
2 |
)d |
2I 0 |
/ 2I 0 |
/4ln2 . (44) |
||||||||||
|
exp( ( ) |
|||||||||||||||
|
Второй член в выражении (43) имеет вид |
|||||||||||||||
|
2 |
2 |
ndxP |
|||||||||||||
|
2I 0 |
exp( ( ) |
)cos( |
)d |
. |
|||||||||||
|
0 |
L |
||||||||||||||
Разлагая функцию 1/( 0 ) в аргументе косинуса в степенной
ряд (ограничиваясь первыми двумя членами) и используя комплексную форму записи волны (имея в виду, что волновая функция − действительная величина), найдем, что второй член в выражении (43) сводится к интегралу Фурье. Действительно,
|
2 ndx |
2 ndx |
|||||||||||||||||||
|
) exp( ( )2 )exp( i |
||||||||||||||||||||
|
2I 0 exp(i |
P |
2 |
P |
)d |
||||||||||||||||
|
L |
L |
|||||||||||||||||||
|
0 |
0 |
|||||||||||||||||||
|
2 ndx |
2 ndx |
|||||||||||||||||||
|
2I 0 |
/ exp |
( |
2 |
P |
)2 /4 cos( |
P |
) |
|||||||||||||
|
L |
L |
|||||||||||||||||||
|
0 |
0 |
|||||||||||||||||||
|
2I 0 |
2 ndx |
|||||||||||||||||||
|
/4ln2exp ( 2 |
L P )2 |
( )2 /16ln2 |
||||||||||||||||||
|
0 |
||||||||||||||||||||
|
cos( |
2 |
ndxP |
). |
(45) |
||||||||||||||||
|
L |
||||||||||||||||||||
|
0 |
С учетом (44) и (45) для распределения интенсивности (43) по-
|
лучаем ( |
/4ln2 |
1, а 1/16ln2 0,09 ): |
||||||||||||
|
I (x |
P |
) |
2I |
2I |
0 |
exp |
0,09(2 ndxP )2 |
( )2 |
/ 2 |
|||||
|
0 |
0 |
L |
0 |
|||||||||||
|
46) |
||||||||||||||
|
2 ndxP ). |
||||||||||||||
|
cos( |
||||||||||||||
|
L |
||||||||||||||
|
0 |
В формуле (46) первое слагаемое является величиной постоян-
ной (средняя интенсивность), а член cos(2 ndxP ) во втором сла-
0 L
гаемом обусловливает быстрое чередование интенсивности в зависимости от разности хода в точках наблюдения xP . Множитель
38
|
© www.phys.nsu.ru |
||||||||
|
exp |
0,09(2 |
ndxP |
)2 |
( )2 |
/ 2 |
определяет форму модулирующей |
||
|
0 L |
0 |
|||||||
функции, т. е. характеризует ухудшение контраста интерференционных полос по мере увеличения разности хода.
Для видности интерференционной картины (10) в соответствии с выражением (46) имеем:
|
V (x |
) exp |
0,09(2 |
ndxP |
)2 ( )2 |
/ 2 |
. |
(47) |
||
|
P |
|||||||||
|
0 L |
0 |
||||||||
Таким образом, кривая видности полос (степени временной когерентности) описывается гауссовой функцией.
|
При разностях хода |
(nd /L)x |
P |
0,17 2 |
/ |
(величина 2 |
/ |
|
0 |
0 |
имеет смысл средней длины когерентности) амплитуда остается приблизительно постоянной (видность V 0,9) и распределение
интенсивности (46) служит хорошим приближением к косинусоидальной волне с длиной 0 . С увеличением разности хода ампли-
туда начинает спадать. Она уменьшается в 10 и более раз (видность V 0,1) при разностях хода (nd /L)xP 0,8 02 / . Это будет наблюдаться для порядков интерференции m 0,8 0 / , что служит
вподдержку результатов качественного анализа (23).
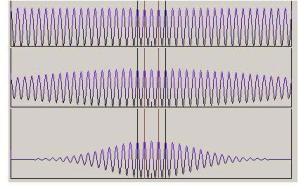
Вкачестве примера на рис. 12 приведены распределения интенсивности при различных значениях ширины спектра источника излучения. Верхняя кривая соответствует модели монохроматического источника, а нижние кривые − излучению источника с увеличивающейся шириной спектра.
Заметим, что для реального (немонохроматического) источника распределение интенсивности вблизи центра картины (низкие порядки интерференции) близко к идеализированному приближению монохроматической волны. Однако для более высоких порядков интерференции (с увеличением разности хода) наблюдается уменьшение глубины модуляции интенсивности в интерференционной картине.
Таким образом, влияние ширины спектра источника света (частичной временной когерентности) проявляется в уменьшении глубины модуляции интенсивности в интерференционной картине.
39
© www.phys.nsu.ru
Рис. 12. Влияние ширины спектра источника света на распределение интенсивности в интерференционной картине. Увеличение ширины спектра − сверху вниз
Измеряя видность полос, можно определить спектральный состав излучения. Следует отметить, что на этом основан метод Фу- рье-спектроскопии [6].
Влияние протяженности источника света на видность интерференционной картины
Пусть число осцилляторов, образующих щель S (см. рис. 4), достаточно велико, и их распределение можно считать непрерывным. Разобьем щель на элементарные светящиеся полоски шириной dx , перпендикулярные к плоскости рис. 8. Положим (I0 /a)dx
− интенсивность излучения, испущенного элементарной полоской (однородное распределение излучения с интенсивностью I0 от
всей щели S ). Интенсивность, создаваемая в точке наблюдения xP
(см. рис. 7) полоской шириной dx с координатой x в плоскости щели S , согласно формуле (29), равна
|
dI (xP ,x) 2I0 |
/a 1 |
cos |
2 |
(nd xP nd x) dx , |
(48) |
||
|
L |
l |
40
© www.phys.nsu.ru
где (nd /l)x − дополнительная оптическая разность хода в точке xP (в приближении a l , d l ), обусловленная смещением ис-
точника S в положение S (n − показатель преломления среды). Для полной интенсивности в точке xP , создаваемой всей щелью S ,
получим выражение (используя комплексную форму записи волны)
|
a /2 |
a /2 |
2 |
nd |
nd |
||||||||||||||
|
I (xP ) 2I0 |
/a |
dx 2I0 /a exp |
( |
xP |
||||||||||||||
|
i |
L |
l |
x) dx . (49) |
|||||||||||||||
|
a /2 |
a /2 |
|||||||||||||||||
|
Вычисляя (49), находим |
nd |
|||||||||||||||||
|
I (x |
P |
) 2I |
0 |
2I |
0 |
sin( l |
a) |
cos( |
2 nd x |
P |
) . |
(50) |
||||||
|
( |
nd |
a) |
L |
|||||||||||||||
|
l |
В выражении (50) первый член определяет среднюю интенсивность, а множитель sin( ndl a)/( ndl a) второго члена влияет на
глубину модуляции интенсивности (контраст) в интерференционной картине.
В соответствии с соотношением (10) видность полос выражает-
|
ся формулой |
|||||||
|
sin( nd a) |
|||||||
|
V |
l |
. |
(51) |
||||
|
nd a) |
|||||||
|
( |
|||||||
|
l |
Итак, видность интерференционной картины (степень пространственной когерентности) зависит от угловой ширины источника a .
Видность остается сравнительно высокой (V 0,9), если ширина щели a 0,25 /(nd /l) или если разность фаз в точках S1 и S2
от осциллятора, расположенного на краю источника S , не превышает /4 (см. рис. 4). При этом распределение интенсивности (50) служит хорошим приближением к идеализированному случаю точечного источника. С увеличением ширины щели видность непрерывно падает. Она становится равной нулю, когда
|
nd a |
или a |
l |
. |
|
|
l |
nd |
41

© www.phys.nsu.ru
При этом оптическая разность хода в точках S1 и S2 от осциллято-
ра, расположенного на краю источника S , равна /2 (сдвиг интерференционной картины в плоскости наблюдения на половину расстояния между линиями равной интенсивности), и интерференционная картина исчезает.
Условие достаточно резкой интерференционной картины можно записать в виде
что служит в поддержку результатов качественного анализа, проведенного ранее (26), показатель преломления n = 1).
Так как функция видности (51) осциллирующая и быстро спадающая функция, то при дальнейшем увеличении ширины щели a видность не превышает значения V 0,2 .
В качестве примера на рис. 13 приведены распределения интенсивности при различных значениях ширины первичного источника излучения. Левая кривая соответствует модели идеализированного источника, а две кривые в центре − излучению источника с увеличивающейся шириной. Крайняя правая кривая показывает последующее увеличение видности интерференционной картины при уменьшении расстояния между щелями S1 и S2 (ширина первич-
ного источника S зафиксирована).
Видно, что глубина модуляции интенсивности (контраст) в интерференционной картине зависит от протяженности первичного источника и расстояния между двумя щелями.
Рис. 13. Влияние протяженности источника света на распределение интенсивности в интерференционной картине. Увеличение ширины источника − слева направо
Таким образом, влияние протяженности источника света (частичной пространственной когерентности) проявляется в уменьшении видности интерференционной картины, обусловленном сме-
42
© www.phys.nsu.ru
щением интерференционных полос от различных точек источника. Измеряя видность полос, можно определить угловой размер источника. Такая возможность реализована практически в звездном интерферометре, предложенном Физо и Майкельсоном [1].
43
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 августа 2021 года; проверки требуют 4 правки.
| Квантовая механика |
|---|
|
|
Основа
|
|
Фундаментальные понятия
|
|
Эксперименты
|
|
Формулировки
|
|
Уравнения
|
|
Интерпретации
|
|
Развитие теории
|
|
Сложные темы
|
|
Известные учёные
|
|
См. также
|
| См. также: Портал:Физика |
Опыт Юнга (эксперимент на двух щелях, также известный как двухщелевой интерферометр Юнга) — первый вариант двухщелевого опыта, проведённого Томасом Юнгом, который демонстрирует интерференцию и дифракцию света, что является доказательством справедливости волновой теории света. Результаты эксперимента были опубликованы в 1803 году.
Описание опыта[править | править код]
В опыте пучок монохроматического света направляется на непрозрачный экран-ширму с двумя параллельными прорезями (щелями), позади которого устанавливается проекционный экран. Ширину прорезей стараются сделать как можно ближе к длине волны излучаемого света (влияние ширины прорезей на интерференцию рассматривается ниже). На проекционном экране получается целый ряд чередующихся интерференционных полос, что и было продемонстрировано Томасом Юнгом.
Если исходить из того, что свет состоит из частиц (корпускулярная теория света), то на проекционном экране можно было бы увидеть только две параллельные полосы света, прошедшие через щели. Между ними проекционный экран оставался бы практически неосвещённым.
С другой стороны, если предположить, что свет представляет собой распространяющиеся волны (волновая теория света), то, согласно принципу Гюйгенса, каждая щель является источником вторичных волн.
Вторичные волны достигнут точек, находящихся на равном удалении от щелей, в одной фазе, следовательно, на серединной линии экрана их амплитуды сложатся, что создаст максимум яркости. То есть, главный, наиболее яркий максимум окажется там, где, согласно корпускулярной теории, яркость должна быть нулевой. Боковые максимумы расположатся симметрично по обеим сторонам в точках, для которых разность хода световых пучков равна целому числу волн.
С другой стороны, в тех точках на удалении от центральной линии, где разность хода равна нечётному числу полуволн, волны окажутся в противофазе — их амплитуды компенсируются, что создаст минимумы яркости (тёмные полосы).
Таким образом, по мере удаления от средней линии яркость периодически изменяется, возрастая до максимума и снова убывая.
Условия для интерференции[править | править код]
Когерентность источника света[править | править код]
Интерференцию возможно наблюдать только для когерентных источников света, но создать два различных когерентных источника практически невозможно. Поэтому все интерференционные опыты базируются на создании при помощи различных оптических систем двух или нескольких вторичных источников из одного первичного, которые будут когерентны. В опыте Юнга когерентными источниками являются две щели в экране.
Влияние ширины щелей[править | править код]
Интерференционная картина возникает на экране, когда ширина щелей приближается к длине волны излучаемого монохроматического света. Если ширину прорезей увеличивать, то освещённость экрана будет возрастать, но выраженность минимумов и максимумов интерференционной картины будет падать вплоть до полного её исчезновения.
Влияние расстояния между щелями[править | править код]
Частота следования интерференционных полос увеличивается прямо пропорционально расстоянию между щелями, в то время как ширина дифракционной картины остаётся неизменной и зависит только от ширины щелей.
Эксперимент с точечным источником света[править | править код]
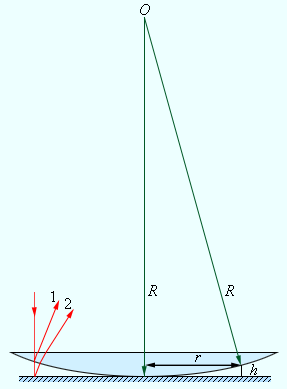
Пусть S — точечный источник света, расположенный перед экраном с двумя параллельными щелями 

Точка М на экране характеризуется одной координатой x — расстоянием между М и ортогональной проекцией S на экране.
Пусть в М падают одновременно два пучка из 

где 
Из прямоугольных треугольников:


Тогда:

и
![{displaystyle delta ={S_{1}M^{2}-S_{2}M^{2} over S_{1}M+S_{2}M}={[D^{2}+(x-a/2)^{2}]-[D^{2}+(x+a/2)^{2}] over S_{1}M+S_{2}M}={(x-a/2)^{2}-(x+a/2)^{2} over S_{1}M+S_{2}M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409b8638741a5327863a6e498303a83e5ef6a0e6)
Далее

Для описания интерференционной картины важна лишь абсолютная величина разности хода, так что знак минус можно опустить.
Если a<<D и x<<D, то 
где 
Яркие полосы — интерференционные максимумы — появляются, когда разность хода равна целому числу длин волн 

Тёмные полосы — минимумы — при разности хода, равной нечётному числу полуволн: 
Освещённость — Е в точке М связана с разницей оптической длины путей следующим соотношением:
где:
Освещённость, таким образом, периодически изменяется от нуля до 

При использовании немонохроматического света максимумы и минимумы для разных длин волн оказываются смещены друг относительно друга, и наблюдаются спектральные полосы.
Интерференция и квантовая теория[править | править код]
Каждое событие, как, например, прохождение света от источника S до точки M на экране через отверстие 

Для того, чтобы знать вероятность того, что свет дойдёт из источника S до точки M, нужно брать во внимание все возможные пути света из точки S до точки М. В квантовой механике этот принцип является фундаментальным. Для получения вероятности P того, что свет дойдёт из точки S до точки М, используется следующая аксиома квантовой механики:

где:
Изменение фазы подобно вращению векторов. Сумма двух векторов изменяется от нуля до максимума 
Демонстрация[править | править код]
Схема Юнга не относится к числу светосильных, демонстрирование её поэтому затруднено.
Со светом[править | править код]
Опыт Юнга с двумя щелями повторить вне лаборатории непросто, так как непросто изготовить подходящей ширины щели. Однако с успехом можно воспроизвести самыми простыми средствами опыт интерференции от двух малых отверстий, суть происходящих при этом физических явлений не изменяется.
Постановка опыта такова: в фольге от шоколадки следует самой тонкой швейной (лучше бисерной) новой иглой проделать два чрезвычайно тонких отверстия как можно ближе друг к другу. Не следует пропускать иглу насквозь, нужно лишь наколоть отверстия самым кончиком. Далее в хорошо затемнённой комнате осветить место проколов мощным источником света. Удобно воспользоваться лазерной указкой, так как её свет монохроматичен. На экране, расположенном в 0,5—1 метре удаётся наблюдать дифракционную картину и интерференционные полосы.
С механическими волнами[править | править код]
Опыт Юнга хорошо демонстрируется для большой аудитории в проекции на экран из волновой ванны, входящей в оборудование физических кабинетов. Чрезвычайно полезно освещать ванну стробоскопом.
См. также[править | править код]
- Билинза Бийе
- Бипризма Френеля
- Зеркала Френеля
- Зеркало Ллойда
- Эффект Ааронова — Бома
- Двухщелевой опыт
- Квантовый ластик с отложенным выбором
Ссылки[править | править код]
- Опыт Юнга (Java-аплет)
- Интерференция — опыт Юнга Архивная копия от 13 ноября 2016 на Wayback Machine (Java-аплет)
















![{displaystyle E=2E_{0}left[1+cos left({frac {2pi delta (M)}{lambda }}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5146ceffbcc5e1358c91e78a9c9265f5558e81f8)



