Нам необходимо определить протяженность всего туристического маршрута.
Для решения данной задачи и ответа на поставленный вопрос нам нужно:
- обозначить искомую длину туристического маршрута как неизвестную переменную х;
- составить пропорцию;
- найти решение данной пропорции тем самым найти ответ на вопрос задачи;
- записать полученный ответ.
Составим пропорцию
Для наглядности и простоты понимания решения данной задачи нам удобно будет составить пропорцию в которой:
- обозначим искомую длину туристического маршрута как переменную х;
- возьмем данную переменную как целое, то есть приравняем её к единице;
- согласно условию данной задачи приравняем 1/6 часть всего пути к 12 километрам.
Такими образом из всего вышесказанного и условия задачи мы получаем, что наша пропорция будет иметь следующий вид:
x = 1
12 = 1/6
Найдем полную длину туристического маршрута
Для этого нам необходимо выразить из полученной пропорции нашу искомую переменную х и воспользоваться для этого правилом пропорции или правилом креста. Данные правила мы можем сформировать следующим образом:
Произведение крайних членов нашей пропорции соответственно равно произведению ее средних членов.
Также мы можем записать, что если на нашей пропорции нарисовать крест то произведения членов находящихся на концах данного креста будут соответственно равны.
Исходя из этого мы получаем следующее равенство:
x * 1/6 = 12 * 1
Выразим из полученного равенства нашу переменную:
x = 12 * 1 / 1/6 = 12 / 1/6 = 12 * 6/1 = 12 * 6 = 72
То есть весь туристический маршрут составляет 72 километра.
Ответ: 72 км.
Как найти длину пути
Отправляясь в поход, лучше заранее найти длину пути, который вам предстоит пройти. Если путешествие автомобильное, то зная протяженность дороги, можно рассчитать количество топлива. Пешим туристам длина маршрута понадобится для оценки времени и запасов продовольствия. Даже отправляясь в гости, желательно поточнее определить длину пути, чтобы не оказаться в положении нежданного гостя.

Вам понадобится
- – линейка;
- – циркуль;
- – крупномасштабная карта;
- – курвиметр;
- – полоска бумаги.
Инструкция
Чтобы найти длину предполагаемого или пройденного пути, возьмите крупномасштабную карту и начертите на ней весь маршрут. Чтобы получить более точные результаты, пройденный путь лучше отмечать во время путешествия, а не после него. Если поездка состоялась на автомобиле, то восстановить траекторию можно на основе отмеченных на карте дорог. Однако, если во время путешествия случались возвраты, объезды или передвижения по проселочным (грунтовым) дорогам, то обозначить пройденный путь будет довольно-таки затруднительно.
Если маршрут начерчен ориентировочно или не требуется большая точность измерений, то можно обойтись лишь циркулем и линейкой. Для этого возьмите циркуль, раздвиньте его ножки на один сантиметр и «пройдитесь» им по отмеченному на карте маршруту. Затем умножьте количество «шагов» циркуля на масштаб карты (количество километров в одном сантиметре) – получится длина пути в километрах. Последний участок маршрута измерьте линейкой, переведите миллиметры в сантиметры и также умножьте на масштаб карты. После чего прибавьте длину этого участка к длине пути, измеренной с помощью циркуля.
Если маршрут пришлось чертить на мелкомасштабной карте или дорога была очень извилистой, то расстояние между ножками циркуля выберите равным 0,5 см. В этом случае, при расчете длины пути, количество шагов циркуля предварительно разделите на два.
Если же, наоборот, карта оказалась крупномасштабной (топографической) или маршрут был достаточно прямолинейным (автомобильная или железная дорога), то зафиксируйте расстояние между ножками циркуля равным нескольким сантиметрам. Это позволит ускорить измерения и не ошибиться при подсчете шагов циркуля. При окончательном расчете длины пути не забудьте умножить количество шагов на расстояние (количество сантиметров) между иголками циркуля.
Если в маршруте встречаются очень извилистые участки (русла рек, осмотр достопримечательностей), то для более точного измерения их длины возьмите полоску тонкой бумаги. Поставьте ее на ребро и проложите вдоль всего маршрута. Затем измерьте длину полоски с помощью линейки. Этот способ измерения длины пути желательно комбинировать с вышеописанными, так как он пригоден лишь для небольших участков.
Чтобы получить наиболее точные результаты измерений, возьмите прибор, называемый курвиметром. Он представляет из себя колесико и счетчик его оборотов. Так как длина окружности колесика и масштаб карты известны, то просто перемножьте число оборотов, периметр колесика (в сантиметрах) и масштаб (количество километров в одном сантиметре). Профессиональный курвиметр произведет все расчеты автоматически – просто сообщите ему масштаб и «прокатитесь» по отмеченному на карте маршруту.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Туристы пролетели на самолёте 2050км и проплыли на корабле 817 км. После этого им ещё осталось проехать на автобусе 336 км и пройти пешком в 21 раз меньше, чем проехали на автобусе. Найти длину всего маршрута.
Светило науки – 481 ответ – 0 раз оказано помощи
Ответ:
Пошаговое объяснение:2050+817+336=3203 км на транспорте
336:21=16 км пешком
3203+16=3219 км всего

Светило науки – 15 ответов – 0 раз оказано помощи
Ответ:
Длина маршрута равна 3219 км
Объяснение:
1)336:21=16(км) – осталось пройти пешком
2)2050+817+336+16=3219(км) – длина маршрута
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория – форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) – в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 – t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость – векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ – средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
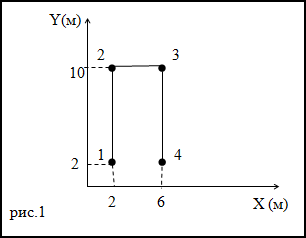
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
