Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Все формулы сторон прямоугольного треугольника
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



- Подробности
-
Автор: Administrator
-
Опубликовано: 12 октября 2011
-
Обновлено: 13 августа 2021
-
Сторона прямоугольного треугольника
В прямоугольном треугольнике стороны связаны между собой наиболее тесным образом. Помимо теоремы Пифагора, которая позволяет найти катет или найти гипотенузу, зная две другие стороны, в прямоугольном треугольнике можно использовать также функции синуса, косинуса, тангенса и котангенса, если известна только одна сторона и любой угол, кроме прямого.
По теореме Пифагора, для того чтобы вычислить гипотенузу прямоугольного треугольника, нужно извлечь квадратный корень из суммы квадратов катетов. Катетами считаются стороны a и b, образующие друг с другом прямой угол, а гипотенузой – сторона, лежащая напротив него.

Гипотенуза всегда будет длиннее суммы катетов, поэтому в формуле для ее вычисления также будет сумма, а в формуле для нахождения катетов будет разность.

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет


где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам


где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу


где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол


где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними


где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании


где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними


где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании


где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь


где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту


где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности


где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности


где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)


где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)


где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Как найти стороны прямоугольного треугольника, зная площадь
В прямоугольном треугольнике один угол прямой, другие два – острые. Сторона, противостоящая прямому углу, называется гипотенузой, другие две стороны – катеты. Зная площадь прямоугольного треугольника, можно вычислить стороны по известной формуле.
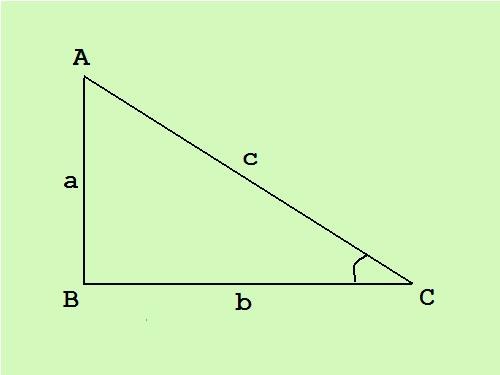
Инструкция
В прямоугольном треугольнике катеты перпендикулярны друг другу, следовательно, общая формула площади треугольника S = (c*h)/2 (где с – основание, а h – высота, проведенная к этому основанию) превращается в половину произведения длин катетов S = (a*b)/2.
Задача 1.
Найдите длины всех сторон прямоугольного треугольника, если известно, что длина одного катета превышает длину другого на 1 см, а площадь треугольника равна 28 см.
Решение.
Запишите основную формулу площади S = (a*b)/2 = 28. Известно, что b = a + 1, подставьте это значение в формулу: 28 = (a*(a+1))/2.
Раскройте скобки, получите квадратное уравнение с одной неизвестной a^2 + a – 56 = 0.
Найдите корни этого уравнения, для чего посчитайте дискриминант D = 1 + 224 = 225. Уравнение имеет два решения: a_1 = (-1 + √225)/2 = (-1 + 15)/2 = 7 и a_2 = (-1 – √225)/2 = (-1 – 15)/2 = -8.
Второй корень не имеет смысла, поскольку длина отрезка не может быть отрицательной величиной, так что a = 7 (см).
Найдите длину второго катета b = a + 1 = 8 (см).
Осталось найти длину третьей стороны. По теореме Пифагора для прямоугольного треугольника c^2 = a^2 + b^2 = 49 + 64, отсюда c = √(49 + 64) = √113 ≈ 10.6 (см).
Задача 2.
Найдите длины всех сторон прямоугольного треугольника, если известно, что его площадь равна 14 см, а угол ACB равен 30°.
Решение.
Запишите основную формулу S = (a*b)/2 = 14.
Теперь выразите длины катетов через произведение гипотенузы и тригонометрических функций по свойству прямоугольного треугольника:
a = c*cos(ACB) = c*cos(30°) = c*(√3/2) ≈ 0.87*c.
b = c*sin(ACB) = c*sin(30°) = c*(1/2) = 0.5*c.
Подставьте полученные значения в формулу площади:
14 = (0.87*0.5*c^2)/2, откуда:
28 ≈ 0.435*c^2 → c = √64.4 ≈ 8 (см).
Вы нашли длину гипотенузы, теперь найдите длины двух других сторон:
a = 0.87*c = 0.87*8 ≈ 7 (см), b = 0.5*c = 0.5*8 = 4 (см).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
