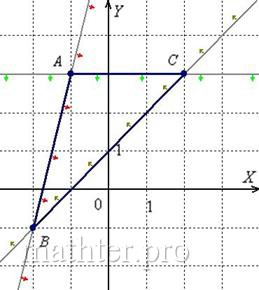
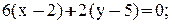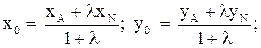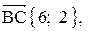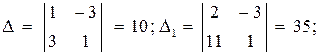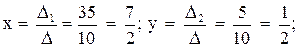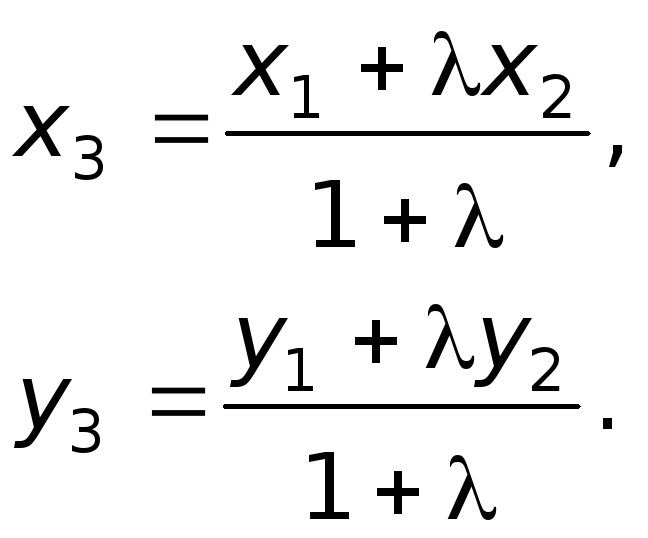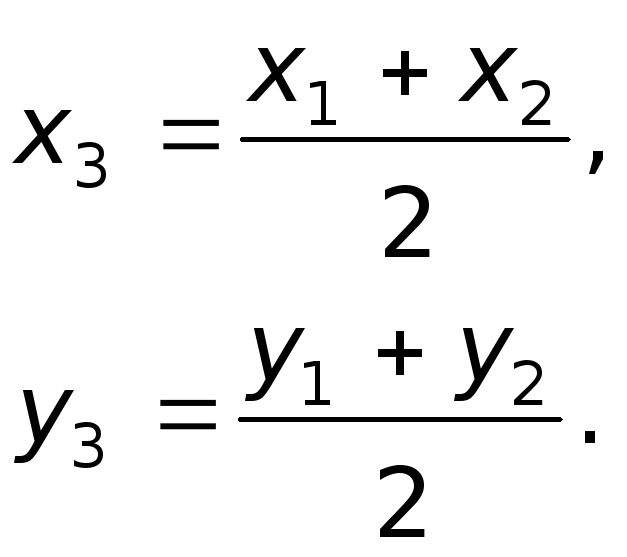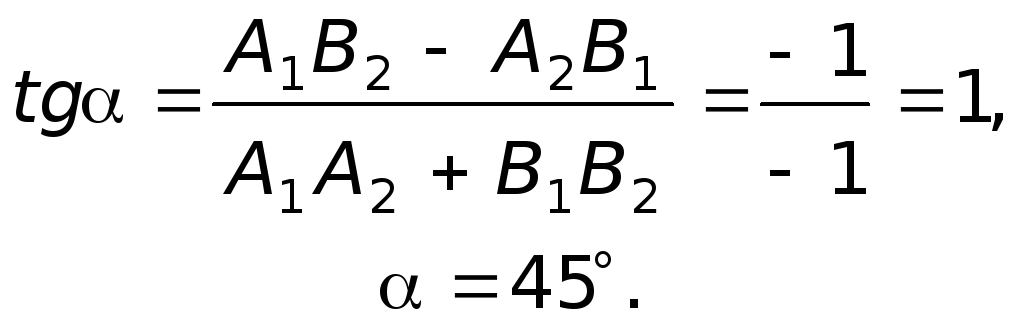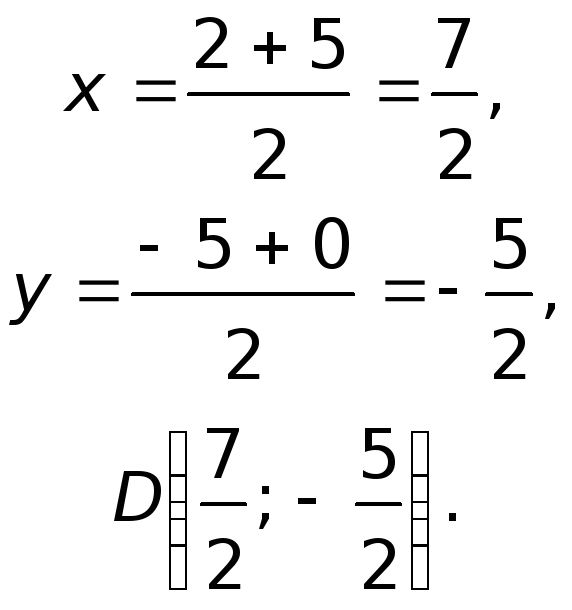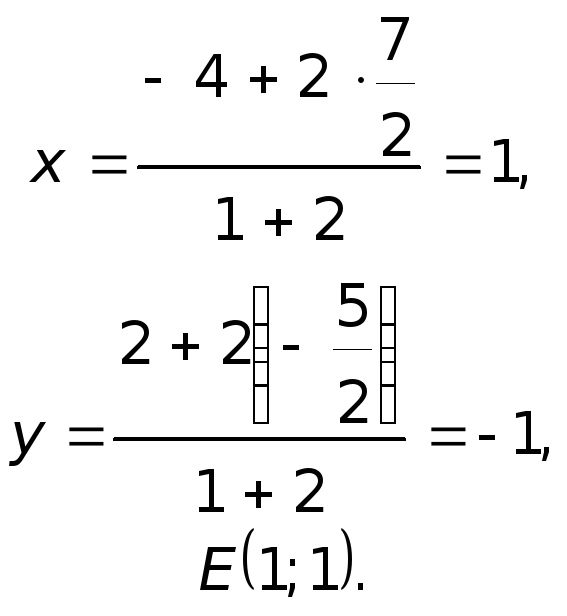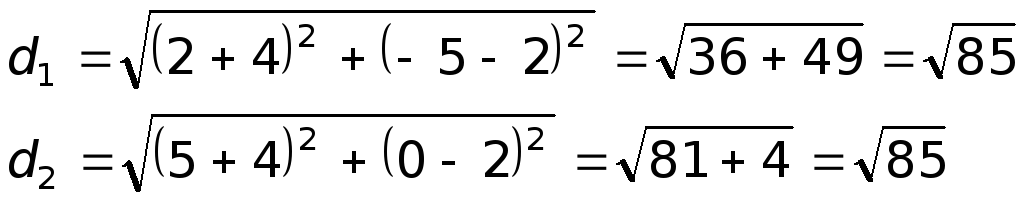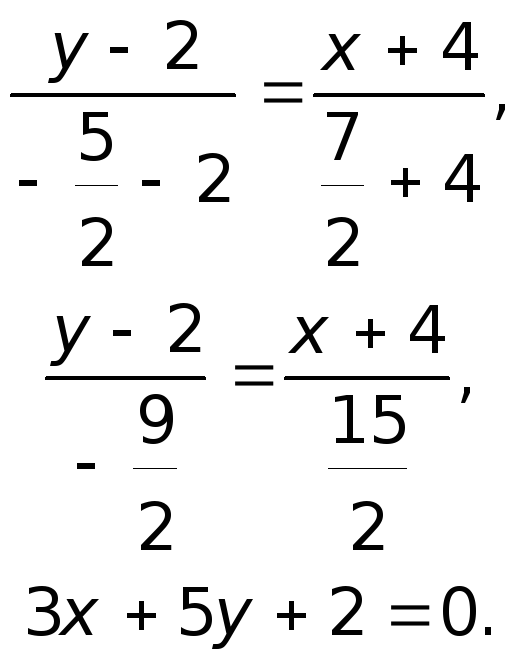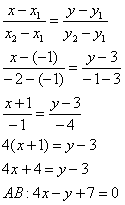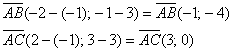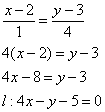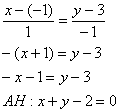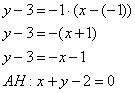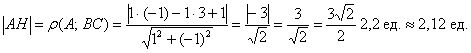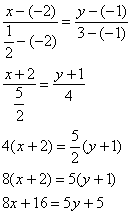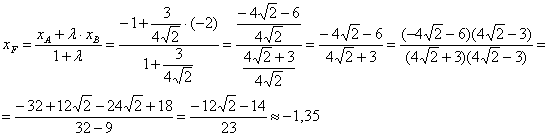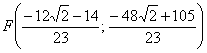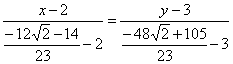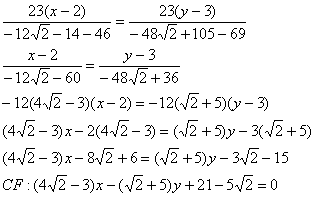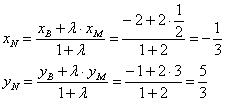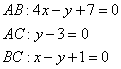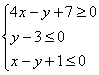Как найти длину высоты через уравнение прямой

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Уравнение высоты треугольника по координатам формула

Как составить уравнение высоты треугольника по координатам его вершин?

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Даны координаты вершин треугольника .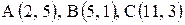

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

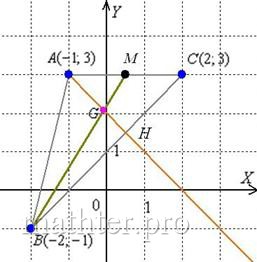
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

1. Длина стороны ВС равна модулю вектора .

; .

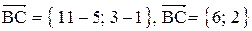
2. Уравнение прямой ВС: ; ; .

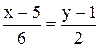
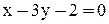
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

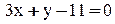
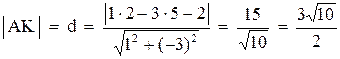
4. Найдем координаты точки N – середины стороны ВС:

; ; .

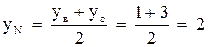
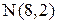
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

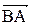
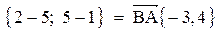
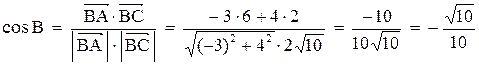
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

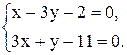
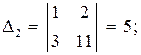
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

Точка К является серединой отрезка АМ.

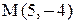
Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	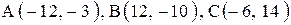.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	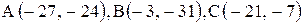.	10.	.
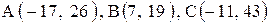11.	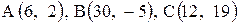.	12.	.
13.	.	14.	.
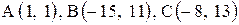15.	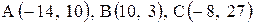.	16.	.
17.	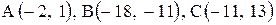.	18.	.
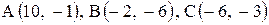19.	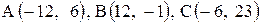.	20.	.
21.	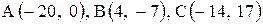.	22.	.
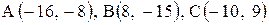23.	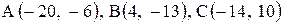.	24.	.
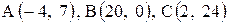25.	.	26.	.
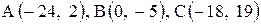27.	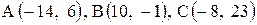.	28.	.
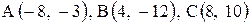29.	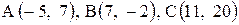.	30.	.

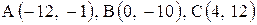Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10637 – | 8008 – или читать все.

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @

Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)

Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:

Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0

Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9

Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:

y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.

10 = (32/3) + d,
d = -2/3

Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0

Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: X_E = 6, Y_E = -1

Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.

(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0

Это уравнение медианы AE.

Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:

S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

источники:

http://4apple.org/uravnenie-vysoty-treugolnika-po-koordinatam/

http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-vershiny-treugolnika-abc

Источник

Как составить уравнение высоты треугольника по координатам его вершин?

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Пример.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

Решение:

1) Составим уравнение стороны BC треугольника ABC.

$[left{ begin{array}{l} - 3 = k cdot 5 + b; \ 8 = k cdot 1 + b; \ end{array} right. Rightarrow k = - frac{{11}}{4};b = frac{{43}}{4}.]$

Таким образом, уравнение прямой BC —

$[y = - frac{{11}}{4}x + frac{{43}}{4}.]$

Угловой коэффициент прямой, перпендикулярной BC,

$[k_2 = - frac{1}{{k_1 }} = - frac{1}{{ - frac{{11}}{4}}} = frac{4}{{11}}.]$

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

$[y = frac{4}{{11}}x + b.]$

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

$[2 = frac{4}{{11}} cdot ( - 7) + b, Rightarrow b = frac{{50}}{{11}}.]$

Итак, уравнение высоты, проведённой к стороне BC:

$[y = frac{4}{{11}}x + frac{{50}}{{11}}.]$

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

$[left{ begin{array}{l} 2 = k cdot ( - 7) + b; \ - 3 = k cdot 5 + b; \ end{array} right. Rightarrow k = - frac{5}{{12}};b = - frac{{11}}{{12}}.]$

Уравнение прямой AB:

$[y = - frac{5}{{12}}x - frac{{11}}{{12}}.]$

Угловой коэффициент перпендикулярной ей прямой

$[k_2 = - frac{1}{{k_1 }} = - frac{1}{{ - frac{5}{{12}}}} = frac{{12}}{5} = 2,5.]$

$[left{ begin{array}{l} 2 = k cdot ( - 7) + b; \ 8 = k cdot 1 + b; \ end{array} right. Rightarrow k = frac{3}{4};b = frac{{29}}{4}.]$

Угловой коэффициент прямой, перпендикулярной AC,

$[k_2 = - frac{1}{{k_1 }} = - frac{1}{{frac{3}{4}}} = - frac{4}{3}.]$

Таким образом, уравнение перпендикулярной AC прямой имеет вид

$[y = - frac{4}{3}x + b.]$

Подставив в него координаты точки B(5;-3), найдём b:

$[- 3 = - frac{4}{3} cdot 5 + b, Rightarrow b = frac{{11}}{3}.]$

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

$[y = - frac{4}{3}x + frac{{11}}{3}.]$

Источник

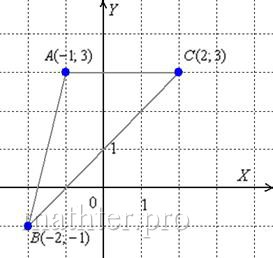
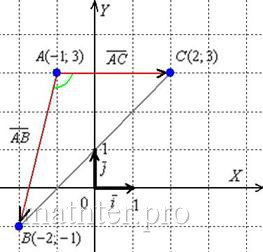
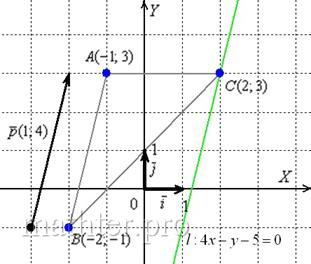
1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)

Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть

(х-0) = k•(-1)

(y-4) = k•(-4)

откуда получаем -х=k и -y/4 +1 = k, приравниваем k

-x = -y/4 + 1 или

4x – y = -4

2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М – середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)

Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)

Получаем (x-3)/2 = (y-1)/0,5

0,5х – 1,5 = 2y – 2

x – 4y = -1

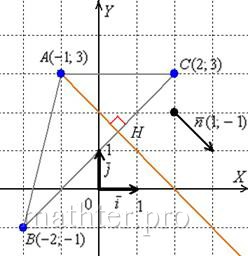
3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0

AB (3-0; 1-4) = AB(3; -3)

CH (x-2; y-(-3))

<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0

3x-6 – 3y – 9 = 0

x-y = 5 – получили уравнение прямой высоты CH

Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)

x+y = 4

Точка Н – пересечение этих двух прямых:

Решая систему уравнений подстановкой, находим х=4,5; y=-0,5

CH (4,5-2; -0,5+3) = CH(2,5; 2,5)

|CH| = √(2,5² + 2,5²) = 2,5•√2

Ответ:

1) 4x – y = -4;

2) x – 4y = -1;

3) 2,5•√2

Источник

Тема
2.2. Прямая на плоскости

Д
ве
взаимно перпендикулярные прямые, на
каждой из которых указано
положительное направление и масштаб,
образуют прямоугольную декартову
систему координат (рис: 2.6). :

Рис. 2.6

Точка

называется началом координат, ось

–
осью абсцисс, ось

-осью ординат. Положение на плоскости
любой точки

определяется двумя числами (координатами):

(рис.2.6).

Теорема 2.9 Расстояние

между точками

и

(рис.2.7) измеряется по
формуле

Рис. 2.7

Теорема 2.10 Если
точка

делит отрезок

в отношении

(
называется коэффициентом
пропорциональности), то ее координаты
находят так;

Следствие В частном случае, когда
отрезок делится пополам,
,
получим так называемые формулы половинного
деления;

Теорема 2.11 Площадь
треугольника

с известными вершинами

равна;

В декартовом базисе прямая изображается
уравнением первой степени с двумя
неизвестными

и

Рассмотрим различные формы задания
уравнения прямой на плоскости.

Теорема 2.12 В прямоугольной системе
координат

любая прямая задается уравнением первой
степени, называемым общим уравнением
прямой

где

– постоянные коэффициенты, причем
.

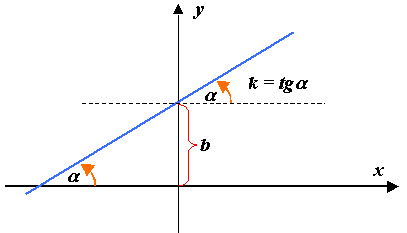
Уравнение прямой с угловым коэффициентом:

З
десь
параметры

и

имеют определенный геометрический
смысл (рис2.8).

Рис. 2.8

и называется угловым коэффициентом.

– угол, образованный прямой
с положительным направлением
.
В качестве положительного направления
измерения угла а принято направление
против хода часовой стрелки (рис.
2.8).

– отрезок, отсекаемый прямой на оси
ординат.

Выполнив несложные алгебраические
преобразования, можно от общего уравнения
прямой перейти к уравнению прямой с
угловым коэффициентом. При этом

Уравнение прямой в отрезках
выглядит так:

Здесь

и
–
отрезки, отсекаемые прямой на осях
абсцисс и ординат соответственно. Их
связь с коэффициентами общего уравнения

В этой форме можно представить уравнение
прямой, не проходящей через начало
координат, т.е. если
.

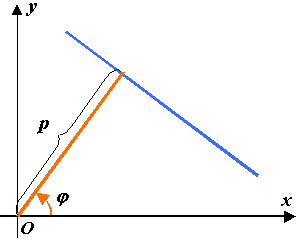
Нормальное уравнение прямой:

Геометрический смысл коэффициентов
этого уравнения:

– длина перпендикуляра,
опущенного из начала координат на
прямую;

– угол, образованный этим перпендикуляром,
с положительным направлением оси
(рис.2.9).

Рис. 2.9

Чтобы перейти к этому виду уравнения
прямой, надо умножить все члены общего
уравнения на нормирующий множитель

Знак

выбирается таким образом, чтобы

Уравнение пучка прямых описывает
множество прямых, проходящих через
точку

с известными координатами:

Уравнение прямой, проходящей через
две точки

и
:

Угол между прямыми

в зависимости от формы задания уравнений
прямых может быть найден по формуле:

или

З
десь
угол

измеряется от прямой с угловым
коэффициентом

или

до прямой с параметрами

или

(рис.2.10):

Рис. 2.10

Из этих формул легко выводятся условия
параллельности:

или

и перпендикулярности прямых:

или
.

Координаты точки пересечения
двух прямых определяются как
решение системы, составленной из
уравнений прямых.

Теорема 2.13
Расстояние

от точки

до прямой

(или
)
определяется по формулам:

или

Задача 2.5 Дано общее уравнение прямой
.

Написать: а) уравнение с угловым
коэффициентом; б) уравнение в отрезках;
в) нормальное уравнение. Построить
прямую.

Решение

а) Оставим член с

слева, а остальные перенесем в правую
часть уравнения. Затем разделим обе
части на коэффициент при
,
т.е. на -3. В результате
получим уравнение с угловым коэффициентом

Задача 2.6 Написать
уравнение прямой, проходящей через
точку

и отсекающей от координатного угла
треугольник, площадью равной
3.

Решение

О
чевидно,
что таких прямых будет 2,
а треугольники образованы во
втором и четвертом квадрантах (рис.2.11):

Рис. 2.11

Запишем уравнение пучка прямых, проходящих
через точку
:

Преобразуем его к уравнению в отрезках:

Таким образом,

Так как

и

имеют разные знаки, то площадь указанных
в условии задачи треугольников может
быть найдена по формуле

Отсюда

или

Решив квадратное уравнение, найдем

Тогда уравнения прямых будут иметь вид:

Задача 2.7 Дан
треугольник с вершинами

и
.
Написать уравнения сторон треугольника,
медианы
,
высоты
,
найти длины медианы

и высоты
,
угол при вершине
,
площадь треугольника
.

Решение

П
остроим
треугольник с указанными вершинами и
отметим все перечисленные элементы
(рис. 2.12).

Рис. 2.12

Уравнения, сторон треугольника получим,
используя уравнения прямой, проходящей
через две точки.

Уравнение

можно было записать и без таких выкладок,
учитывая, что обе точки лежат на оси
.

Для нахождения уравнения медианы

предварительно определим координаты
точки

как середины отрезка
:

Тогда уравнение медианы

будет иметь вид

Длину

определим как расстояние между точками

и
:

Запишем уравнение пучка прямых, проходящих
через вершину
:

Так как высота

перпендикулярна стороне треугольника
,
то их угловые коэффициенты связаны так:

Из уравнения

легко найти

Тогда
,
и уравнение высоты

будет

или

Длину высоты

определим как расстояние от точки

до прямой
:

Так как мы установили общие уравнения
прямых

и
,
то воспользуемся соответствующей
формулой для определения угла при
вершине

треугольника
.

Площадь треугольника

равна

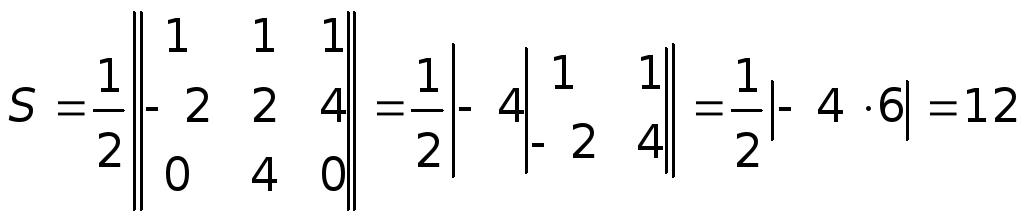
Задача 2.8 Найти
точку пересечения медиан и точку
пересечения высот треугольника, вершины
которого

и
.

Решение

С
троим
треугольник, показываем точки пересечения
его медиан и высот (рис.2.13).

Рис.2.13

Определим координаты точки

как середины отрезка
,
воспользовавшись формулами половинного
деления

Для определения координат точки
пересечения медиан

воспользуемся свойством этой точки,
согласно которому она делит медиану

в отношении
,
считая от вершины, т.е.
.
Тогда для точки

Треугольник

является равнобедренным, так как длины
сторон

и

равны:

Следовательно, медиана

будет и высотой. Отсюда уравнение высоты

определим как уравнение прямой, проходящей
через точки
:

Уравнение пучка прямых, проходящих
через точку

может быть записано как

Уравнение

находим через известные координаты
концов отрезка:

Так как высота

перпендикулярна
,
то ее угловой коэффициент

и уравнение

будет

или

Координаты точки

пересечения высот

и

определим из решения системы, составленной
из уравнений высот:

Соседние файлы в папке высшая математика

Источник

2.9. Типовая задача с треугольником

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в

сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не

будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.

Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется

найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:

Задача 95

Даны вершины треугольника . Требуется:

1) составить уравнения сторон и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить прямой , проходящей через точку параллельно прямой ;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;
8) найти точку пересечения .
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ;
10) найти центр тяжести треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

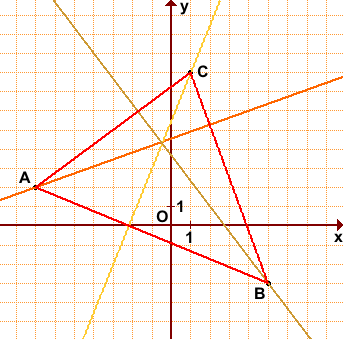
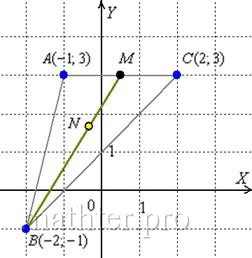
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и

самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:

Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1

см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.

Вперёд без страха и сомнений:

1) Составим уравнения сторон и найдём их угловые

коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум

точкам.

Составим уравнение стороны по точкам :

Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.

Теперь

найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент:

Самостоятельно разбираемся со сторонами и сверяемся, что

получилось:

2) Найдём длину стороны . Используем соответствующую формулу для точек :

Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 🙂

3) Найдём . Это Задача 31, повторим:

Используем формулу .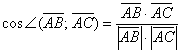
Найдём векторы:

Таким образом:
, и сам угол:
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого

он есть.

Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла

между прямыми, так как они всегда дают острый угол.

4) Составим уравнение прямой , проходящей через точку параллельно прямой . Это стандартная задача, и мы ленимся отработать её вновь!

Из общего уравнения прямой вытащим направляющий вектор .

Составим уравнение прямой по точке и направляющему вектору :

5) Составим уравнение высоты и найдём её длину.
Первую часть задания мы тоже решали:

Из уравнения стороны снимаем вектор нормали . Уравнение высоты

составим по точке и направляющему вектору :

Обратите внимание, что координаты точки нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае , тогда: . Уравнение высоты составим по точке и угловому коэффициенту :

Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим – точку

пересечения высоты и стороны ;

б) находим длину отрезка по двум

известным точкам.

Но зачем? – ведь есть удобная формула расстояния от точки до прямой :

6) Вычислим площадь треугольника. Используем «школьную» формулу:

7) Уравнение медианы составим в два шага:

а) Найдём точку – середину стороны . Используем формулы координат середины отрезка.

Известны концы , и тогда середина:

б) Уравнение медианы составим по точкам :

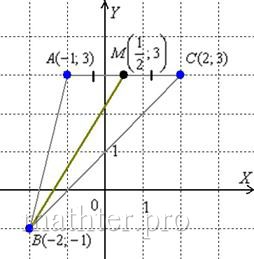
– для проверки подставим координаты точек .

8) Найдём точку пересечения высоты и медианы:
в

Первое уравнение умножили на 5, складываем их почленно:
– подставим в первое уравнение:

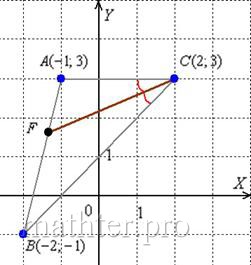
9) Биссектриса делит угол пополам:

Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

Длины сторон уже найдены в предыдущих пунктах: .

Таким образом, . Координаты точки найдём по формулам деления отрезка в данном отношении. Да,

параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки известны и понеслась нелёгкая:

Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение – чтобы использовать формулу и

избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

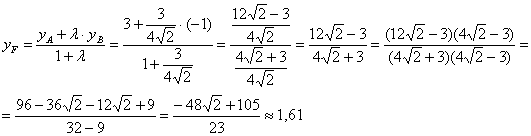
аким образом:

И предчувствие вас не обмануло, уравнение биссектрисы составим по точкам по формуле :

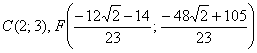
обратите внимание на технику упрощений:

Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)

10) Найдём центр тяжести треугольника.

Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца

в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то

теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.

Из пункта 7 нам уже известна одна из медиан: . Как решить задачу?

Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь

короче! Нужно только знать полезное свойство:

Точка пересечения медиан делит каждую из медиан в

отношении , считая от вершины треугольника. Поэтому справедливо

отношение
Нам известны концы отрезка – точки и .
По формулам деления отрезка в данном отношении:

Таким образом, центр тяжести треугольника:
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные

неравенства:

11) Составим систему линейных неравенств, определяющих треугольник.

Для удобства я перепишу найденные уравнения сторон:

Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится

вершина . Составим вспомогательный многочлен и вычислим его значение в точке : . Поскольку сторона принадлежит треугольнику, то неравенство будет нестрогим: