Как найти длину высоты опущенной из вершины пирамиды на грань и написать ее уравнение….помогите пожалуйста…
Диман
Знаток
(342),
закрыт
13 лет назад
Вершина – S на грань ABC” />
Дополнен 13 лет назад

Вершина – S на грань ABC
Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Как найти высоту пирамиды по векторам
Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x2 – x1; Y = y2 – y1; Z = z2 – z1
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:
Пример №2 . В тетраэдре ABCD вычислить:
- объем тетраэдра ABCD;
- высоту тетраэдра, опущенную из вершины D на грань ABC.
A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)
Ответ
Проверено экспертом
Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .
Находим векторы АВ, АС и АД.
Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.
Определяем векторное произведение АВ х АС.
-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).
Далее находим смешанное произведение (АВ х АС) х АД.
(АВ х АС) = (-5; -10; 0),
(АВ х АС) х АД = 30 + 10 + 0 = 40.
Объем пирамиды равен (1/6) этого произведения:
V = (1/6)*40 = (20/3) куб.ед.
Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).
Площадь основания АВС равна половине модуля векторного произведения АВ х АС.
S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.
h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )
Примечание: дробные числа записывайте
через точку, а не запятую.
Длина и уравнение высоты опущенной из вершины d на плоскость abc
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет – тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку “Зарегистрироваться” вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
Длина и уравнение высоты опущенной из вершины d на плоскость abc
Даны координаты вершин пирамиды ABCD:
A(6;2;3); B(6;5;6); C(3;6;7); D(4;2;2).
Найти: 1) |AB|.
Вектор АВ= = (0; 3; 3).
Длина ребра АВ = √(0² + 3² + 3²) = √18 ≈ 4,242640687.
Скалярное произведение векторов АВ и АС равно:
a · b = ax · bx + ay · by + az · bz = 0 · (-3) + 3 · 4 + 3 · 4 = 0 + 12 + 12 = 24.
3) Проекция вектора AB на AC;
Решение: Пр ba = ( a · b)/ |b|.
Скалярное произведение векторов уже найдено и равно 24.
Найдем модуль вектора:
|b| = √(bx² + by ² + bz ²) = √((-3)² + 4² + 4²) = √(9 + 16 + 16) = √41.
Пр ba = 24/ √41 = 24√41/ 41 ≈ 3,7481703.
4) площадь грани ABC.
S = (1/2)*|AB|*|AC|*sin α = (1/2)*|AB|*|AC|*√(1 – cos²α) .
Найдем угол между ребрами AB(0;3;3) и AC(-3;4;4):
cos α = (0*(-3)+3*4+3*4)/(√18*√41) = 24/√738 = 4√82/41 ≈ 0,883452.
sin α = √(1 – 0,883452 ²) = 0,468521.
S(ABC) = (1/2)* √18*√41*0,468521 = 6,363961.
5) уравнение грани ABC.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1 = 0.
Уравнение плоскости ABC
x-6 y-2 z-3 0 3 3 -3 4 4 = 0. (x-6)(3*4-4*3) – (y-2)(0*4-(-3)*3) + (z-3)(0*4-(-3)*3) = – 9y + 9z-9 = 0.
Упростим выражение: – y + z – 1 = 0.
6) уравнение ребра AD.
Уравнение прямой AD(-2,0,-1)
AD: (x – 6)/(-2) = (y – 2)/0 = (z – 3)/(-1).
Параметрическое уравнение прямой:
x=6-2t
y=2+0t
z=3-t.
7) угол между ребром AD и гранью ABC.
Синус угла γ между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле:
sin γ = |Al+Bm+Cn|/(√A²+B²+C²)*√(l²+m²+n²).
Уравнение плоскости ABC: – y + z-1 = 0
Уравнение прямой AD получено выше.
sin γ = |0*(-2)+(-1)*0+1*(-1)|/(√0²+1²+1²)*√(2²+0²+1²) = 1/(√2*√5) =
= 1/√10 ≈ 0,316228.
γ = arc sin 0,316228 = 0,321751 радиан = 18,43495 °.
8) смешанное произведение (AB, AC, AD) и V – объём пирамиды ABCD.
Произведение векторов a × b = .
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|X1 Y1 Z1|
V = (1/6) |X2 Y2 Z2|
|X3 Y3 Z3|
| 0 3 3|
V = (1/6) |-3 4 4| = 9/6 = 1,5.
|-2 0 -1|
где определитель матрицы равен:
∆ = 0*(4*(-1)-0*4)-(-3)*(3*(-1)-0*3)+(-2)*(3*4-4*3) = -9.
9) уравнение высоты,опущенной из вершины D на грань ABC и
ее длину.
Для вычисления расстояния от точки M(4, 2, 2) до плоскости – y +z -1 = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D|/√(A² + B² + C²)
Подставим в формулу данныеd = |0·4 + (-1)·2 + 1·2 + (-1)|/√((0² + (-1)² + 1²) =
= |0 – 2 + 2 – 1| /√(0² + (-1)² + 1²) = 1/√2 ≈ 0.70710678.
10) уравнение плоскости, проходящей через точку D параллельно грани ABC.
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости ABC: – y + z-1 = 0
0(x-4)-1(y-2)+1(z-2) = 0
или
0x-y+z+0 = 0.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 53926 Дана пирамида с вершинами A(2; 2 — 3),…
Условие
![]()
5f6a06ffb931bd71f10f35dc
06.10.2020 12:40:21
Дана пирамида с вершинами A(2; 2 — 3), В(3; 1;1), С(-1;0; —5), D(4; -2; -3). Найти длину высоты, опущенной из вершины D на грань АВС.
математика ВУЗ
6642
Решение
![]()
5f3ea7e3faf909182968ddd9
06.10.2020 14:44:57
★
Находим площадь треугольника АВС через векторное произведение векторов.
Находим объем пирамиды, как (1/6) модуля смешанного произведения векторов
V=(1/3)S_( Δ ABC)*H
H=3V/S_( Δ ABC)=41/7,5=…


Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
Примеры решения задач
1.
Найти скалярное произведение векторов
![]() и
и![]() .
.
Решение:
По формуле (5.3) находим:
![]() .
.
2.
Векторы
![]() образуют угол
образуют угол![]() .
.
Зная, что![]() ,
,
вычислить![]() .
.
Решение:
Используя свойства скалярного
произведения и формулу (5.1), получаем:
![]()
![]() .
.
3.
Даны вершины треугольника
![]() .
.
Найти: а) внутренний угол при вершинеC;
б)
![]() .
.
Решение:
а) Угол
![]() при вершинеC
при вершинеC
есть угол между векторами
![]()
и
![]() .
.
Определим координаты этих векторов:
![]() ,
,
![]() .
.
Найдем
их модули:
![]() ;
;![]() .
.
Согласно формуле (5.4)
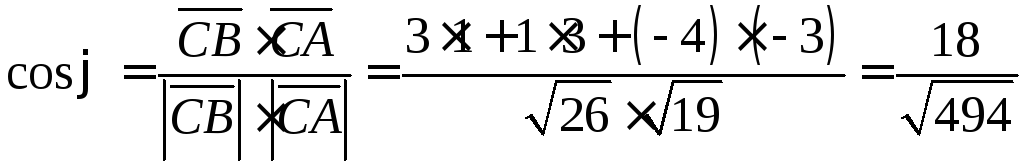 ;
;
 .
.
б)
Из первого свойства скалярного
произведения получаем 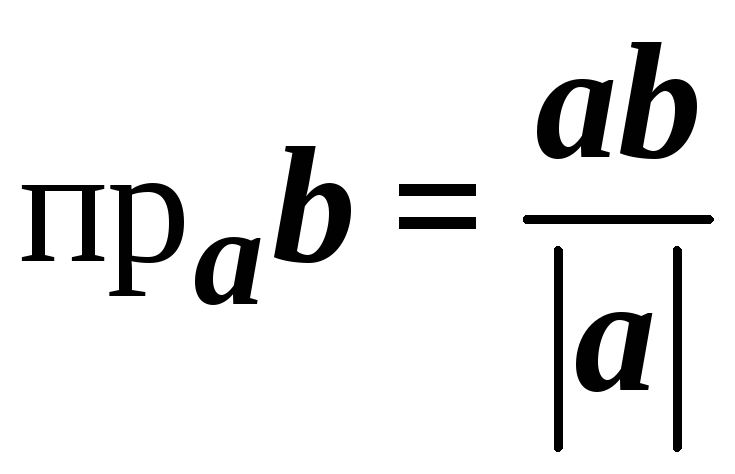 .Поэтому
.Поэтому
![]() =
= .
.
4.
Найти векторное произведение векторов
![]() и
и![]() .
.
Решение:
Имеем по формулам (5.6) и (5.7)
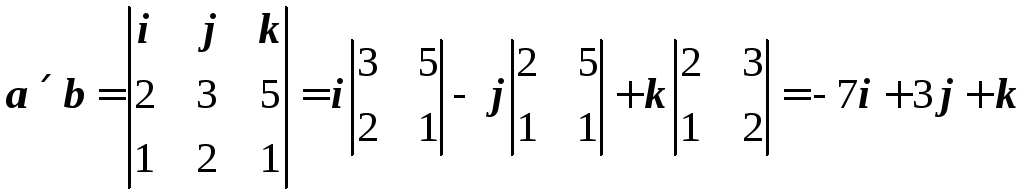 .
.
5.
Вычислить площадь параллелограмма,
построенного на векторах:
![]() и
и![]() .
.
Решение:
Находим векторное произведение
![]() на
на![]() по формулам (5.6) и (5.7):
по формулам (5.6) и (5.7):
 .
.
Так
как модуль векторного произведения
двух векторов равен площади построенного
на них параллелограмма, то
![]() (кв. ед.).
(кв. ед.).
6.
Вычислите площадь треугольника с
вершинами
![]() и
и![]() .
.
Решение:
Площадь треугольника ABC
равна половине площади параллелограмма,
построенного на векторах
![]()
и
![]() .
.
Найдем
координаты
этих векторов ![]() ,
,![]() .
.
Далее находим векторное произведение
этих векторов по формулам (5.6) и (5.7):
 .
.
Тогда
![]() (кв.ед.).
(кв.ед.).
7.
Вычислите площадь параллелограмма,
построенного на векторах
![]()
и
![]() ,
,
если
![]() ,
,
![]() .
.
Решение:
Используя свойства векторного
произведения, имеем
![]()
![]()
(поскольку
![]() ,
,
![]() ).
).
Итак,
![]()
(кв.ед.).
8.
Показать, что векторы
![]() ,
,![]() ,
,![]() компланарны.
компланарны.
Решение:
Воспользуемся условием компаланарности
векторов (5.9). Находим смешанное
произведение векторов:
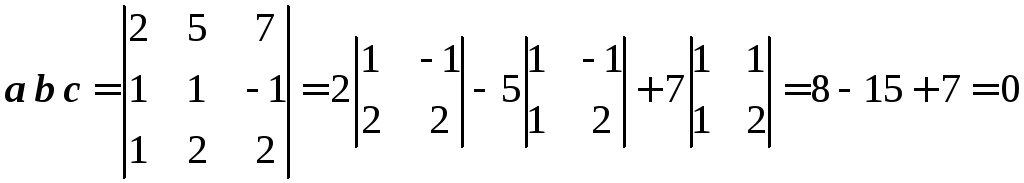 .
.
Так
как , то заданные векторы компланарны.
9.
Доказать, что четыре точки
![]()
лежат
в одной плоскости.
Решение:
Достаточно показать, что три вектора
![]() ,
,
имеющие начало в одной из данных точек,
лежат в одной плоскости (т.е. компланарны).
Находим координаты векторов
![]() ,
,![]() ,
,![]() .
.
Проверяем условие компланарности
векторов (5.9):
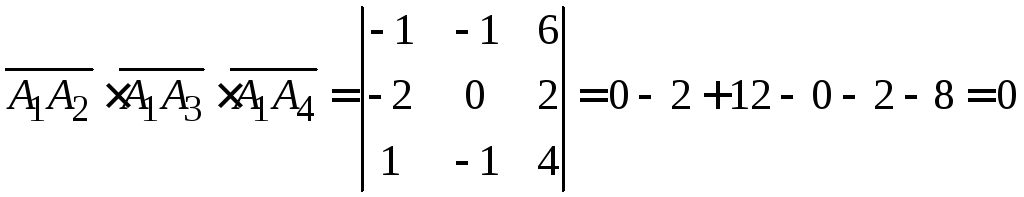 .
.
Итак,
векторы
![]() компланарны, следовательно, точки
компланарны, следовательно, точки![]() лежат в одной плоскости.
лежат в одной плоскости.
10.
Найти объем треугольной пирамиды с
вершинами
![]() .
.
Решение:
Найдем векторы
![]() ,
,
совпадающие с ребрами пирамиды,
сходящимися в вершине A:
![]()
![]() .
.
Смешанное
произведение этих векторов равно по
модулю объему параллелепипеда,
построенного на них. Находим смешанное
произведение этих векторов:
 .
.
Так
как объем пирамиды равен
![]() объема параллелепипеда, построенного
объема параллелепипеда, построенного
на векторах
![]() ,
,
то
![]() (куб.ед.).
(куб.ед.).
11.
Даны вершины пирамиды
![]() .
.
Найти
длину высоты, опущенной из вершины S
на грань ABC.
Решение:
Так как объем пирамиды есть
![]() ,
,
то![]() ,
,
где![]() – высота пирамиды,
– высота пирамиды,![]() – площадь основания пирамиды. Находим
– площадь основания пирамиды. Находим
![]()
![]()
![]() ,
,
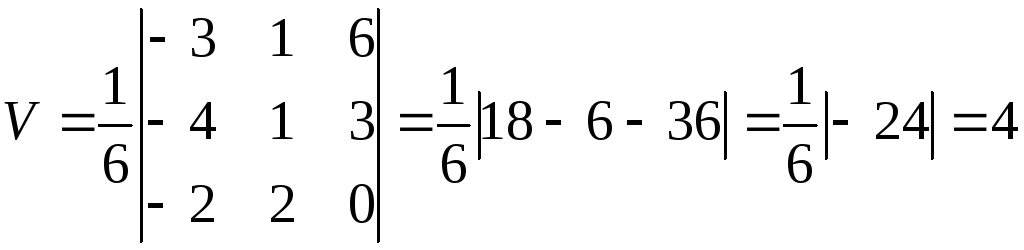 .
.
Находим
:
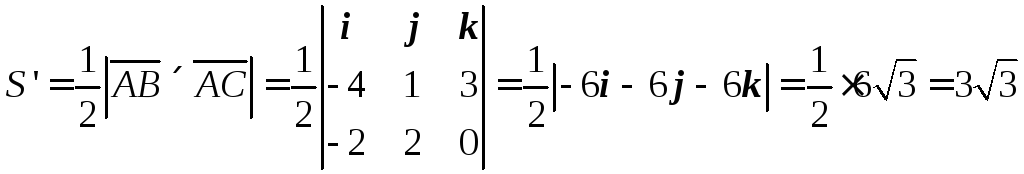 .
.
Следовательно,
![]() .
.
Задачи для самостоятельного решения
1.
Даны векторы
![]() и
и![]() .
.
При каком значении![]()
эти
векторы перпендикулярны?
2.
Определите угол между векторами
![]() и
и![]() .
.
3.
Найти
![]() ,
,
если![]() ,
,![]() .
.
4.
Даны векторы:
![]() ,
,![]() ,
,![]() .
.
Найти![]() .
.
5.
Показать, что четырехугольник с вершинами
![]()
![]()
![]() есть квадрат.
есть квадрат.
6.
Найти векторное произведение векторов
![]() и
и![]() .
.
7.
Найти площадь параллелограмма,
построенного на векторах
![]() и
и![]() .
.
8.
Найдите площадь треугольника с вершинами
![]() .
.
9.
Векторы
![]() составляют угол
составляют угол![]() .
.
Найти площадь параллелограмма,
построенного на векторах![]()
и
![]() ,
,
где![]() .
.
10.
Дано:
![]() ,
,![]() ,
,![]() .
.
Найти![]() .
.
11.
Показать, что точки
![]()
лежат
в одной плоскости.
12.
Найти объем параллелепипеда, построенного
на векторах
![]() ,
,![]() и
и![]() .
.
13.
Найти высоту параллелепипеда, построенного
на векторах
![]() ,
,![]() и
и![]() .
.
Высота опущена на грань, образованную
векторами![]() .
.
14.
Даны векторы
![]() ,
,![]() и
и![]() .
.
Найти:![]() .
.
15.
При каком значении
![]() векторы
векторы![]() и
и![]()
перпендикулярны?
16.
Определите угол между векторами
![]() и
и![]() .
.
17.
Даны векторы
![]() ,
,![]() и
и![]() .
.
Найти![]() .
.
18.
Даны три последовательные вершины
параллелограмма:
![]() .
.
Найти
его
четвертую вершину и угол между векторами
![]() .
.
19.
Найти координаты вектора
![]() ,
,
если![]() ;
;![]() .
.
20.
Найти площадь параллелограмма,
построенного на векторах
![]() и
и![]() .
.
21.
Найти площадь треугольника с вершинами
![]() ,
,
![]()
и
![]() .
.
22.
Векторы
![]()
составляют угол 45o.
Найти площадь треугольника, построенного
на векторах
![]()
и
![]() ,
,
если
![]() .
.
23.
Показать, что векторы
![]() ,
,![]() и
и![]() компланарны.
компланарны.
24.
Найти объем параллелепипеда, построенного
на векторах
![]() ,
,![]() и
и![]() .
.
25.
Даны вершины пирамиды
![]() .
.
Найти
длину высоты, опущенной на грань BCD.
Ответы:
1)
m
= 4;
2)
![]() ;3)
;3)
13; 4)
5; 6)
![]() ;
;
7)
![]() ;
;
8) ![]() ;9)
;9)
![]() ;10)
;10)
![]() ;12)
;12)
12; 13)
![]() ;14)
;14)
(3;3;0); 15)
m
= 1;
16) 135о![]() 17)
17)
−4;
18)
![]() ;19)
;19)
![]() ;20)
;20)
60; 21)
![]() ;22)
;22) ![]() ;24)
;24)
![]() ;25)
;25)
11.
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ 6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
