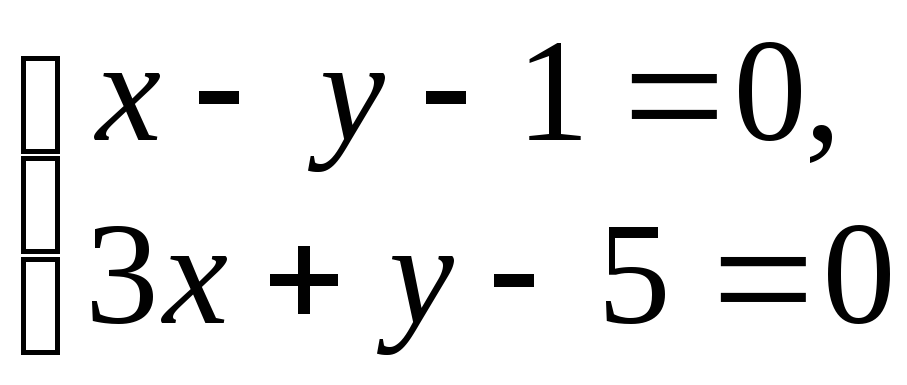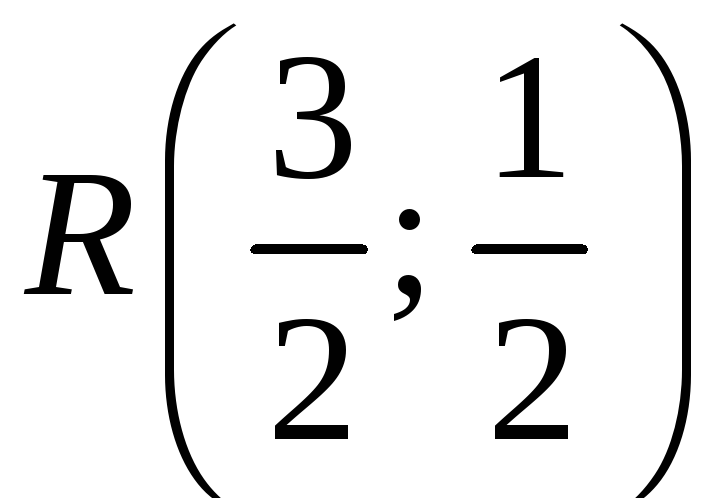Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Юрик
Высший разум
(117860)
12 лет назад
Запишите уравнение стороны, на которую нужно опустить перпендикуляр в общем виде Ах+Ву+С=0. Если координаты третьей вершины (m;n), то уравнение высоты
(x-m)/A=(y-n)/B.
Длина высоты определяется, как расстояние от точки до прямой по формуле
d=|A•m+B•n+C|/√(A²+B²).
P.S. Если треугольник в пространстве, то решение значительно усложняется.
Семен Аркадьевич
Высший разум
(340149)
12 лет назад
1. Составить уравнение той стороны, высоту опущенную на которую требуется найти.
2. Составить уравнение перпендикуляра к стороне по п. 1 через оставшуюся вершину с учетом углового коэффициента полученной стороны.
3. Решить совместно уравнения по п. 1 и п. 2 и найти координаты основания высоты.
4. Найти длину высоты.
Все вопросы в агент.
Alexander Panfilov
Мыслитель
(6234)
12 лет назад
1. Найти длину той стороны, высоту опущенную на которую требуется найти.
2. По известной формуле найти площадь треугольника.
3. Разделить площадь на длину стороны, умножить на два. Получите длину высоты.
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Раздел V.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
В раздел включены
задачи, которые рассматриваются в теме
«Аналитическая геометрия на плоскости
и в пространстве»: составление различных
уравнений прямых на плоскости и в
пространстве; определение взаимного
расположения прямых на плоскости,
прямых, прямой и плоскости, плоскостей
в пространстве; изображение кривых
второго порядка. Необходимо отметить,
что в данном разделе представлены задачи
экономического содержания, при решении
которых применяются сведения из
аналитической геометрии на плоскости.
При решении задач
аналитической геометрии целесообразно
воспользоваться учебными пособиями
следующих авторов: Д.В. Клетеника, Н. Ш.
Кремера, Д.Т. Письменного В.И. Малыхина,
т.к. в данной литературе рассматривается
более широкий круг задач, которые можно
использовать для самостоятельной
подготовки по данной теме. Применение
аналитической геометрии к решению
экономических задач изложено в учебных
изданиях М.С. Красса и В.И. Ермакова.
Задача 5.1. Даны
координаты вершин треугольника АВС.
Необходимо
а) написать
уравнения сторон треугольника;
б) написать
уравнение высоты треугольника проведенной
из вершины С
к стороне АВ
и найти ее длину;
в) написать
уравнение медианы треугольника,
проведенной из вершины В
к стороне АС;
г) найти углы
треугольника и установить его вид
(прямоугольный, остроугольный,
тупоугольный);
д) найти длины
сторон треугольника и определить его
тип (разносторонний, равнобедренный,
равносторонний);
е) найти координаты
центра тяжести (точка пересечения
медиан) треугольника АВС;
ж) найти координаты
ортоцентра (точка пересечения высот)
треугольника АВС.
К каждому из
пунктов а) – в) решения сделать рисунки
в системе координат. На рисунках
обозначить соответствующие пунктам
задачи линии и точки.
Данные к условию
задачи, соответствующие вариантам:
|
1)
2)
3)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17) 18) |
4)
5)
6)
19)
20)
21)
22)
23)
24)
25)
26)
27)
28)
29) 30) |
Пример 5.1
Даны координаты
вершин треугольника АВС:
.
Необходимо а) написать уравнения сторон
треугольника; б) написать уравнение
высоты треугольника проведенной из
вершины С
к стороне АВ
и найти ее длину; в) написать уравнение
медианы треугольника, проведенной из
вершины В
к стороне АС;
г) найти длины сторон треугольника и
определить его тип (разносторонний,
равнобедренный, равносторонний); д)
найти углы треугольника и установить
его вид (прямоугольный, остроугольный,
тупоугольный); е) найти координаты центра
тяжести (точка пересечения медиан)
треугольника АВС;
ж) найти координаты ортоцентра (точка
пересечения высот) треугольника АВС.
Решение
а)
Для каждой стороны треугольника известны
координаты двух точек, которые лежат
на искомых линиях, значит уравнения
сторон треугольника – уравнения прямых,
проходящих через две заданные точки
|
|
(5.1) |
где
и
соответствующие координаты точек.
Таким образом,
подставляя в формулу (5.1) координаты
соответствующих прямым точек получаем
,
,
,
откуда после
преобразований записываем уравнения
сторон
,
,
.
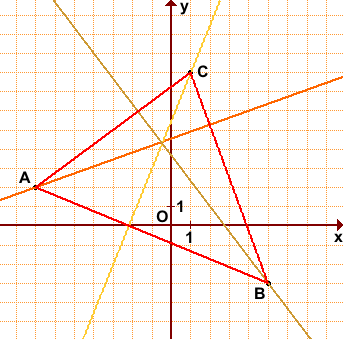
На рис. 7 изобразим
соответствующие сторонам треугольника
прямые.
Ответ:
,
,
.
|
Рис. 7 |
б)
Пусть
– высота, проведенная из вершины
к стороне
.
Поскольку
проходит через точку
перпендикулярно вектору
,
то составим уравнение прямой по следующей
формуле
|
|
(5.2) |
где
– координаты вектора перпендикулярного
искомой прямой,
– координаты точки, принадлежащей этой
прямой. Найдем координаты вектора,
перпендикулярного прямой
,
и подставим в формулу (5.2)
,
,
,
,
.
Найдем длину высоты
CH
как расстояние от точки
до прямой
|
|
(5.3) |
где
– уравнение прямой
,
– координаты точки
.
В предыдущем пункте
было найдено
.
Подставив данные
в формулу (5.3), получим
,
На рис. 8 изобразим
треугольник и найденную высоту СН.
Ответ:
.
|
Р |
в)
медиана
треугольника
делит сторону
на две равные части, т.е. точка
является серединой отрезка
.
Исходя из этого, можно найти координаты
точки
|
|
(5.4) |
где
и
– координаты соответственно точек
и
,
подставив которые в формулы (5.4), получим
;
.
Уравнение медианы
треугольника
составим как уравнение прямой, проходящей
через точки
и
по формуле (5.1)
,
.
Ответ:
(рис. 9).
|
Р |
г)
Длины сторон треугольника найдем как
длины соответствующих векторов, т.е.
,
,
.
Стороны
и
треугольника
равны, значит, треугольник является
равнобедренным с основанием
.
Ответ:
треугольник
равнобедренный с основанием
;
,
.
д)
Углы треугольника
найдем как углы между векторами,
исходящими из соответствующих вершин
данного треугольника, т.е.
,
,
.
Поскольку треугольник
равнобедренный с основанием
,
то
,
Углы между векторами
вычислим по формуле (4.4), для которой
потребуются скалярные произведения
векторов
,
.
Найдем координаты
и модули векторов, необходимых для
вычисления углов
,
;
,
,
.
Подставляя
найденные данные в формулу (4.4), получим
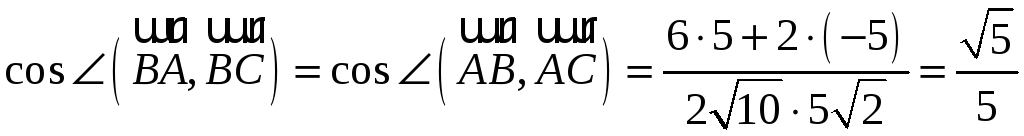
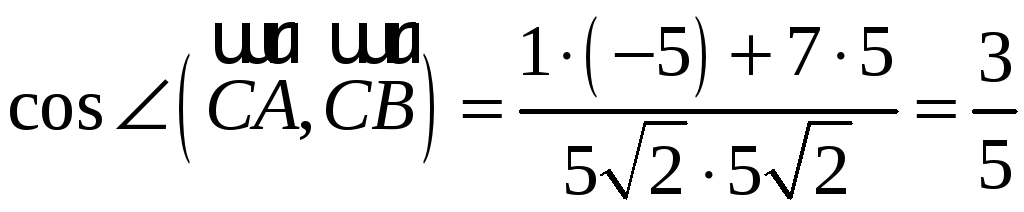
Поскольку значения
косинусов всех найденных углов
положительны, то треугольник
является остроугольным.
Ответ:
треугольник
остроугольный;
,
,
.
е)
Пусть
– центр тяжести треугольника
,
тогда координаты
точки
можно найти, по формулам (5.5)
|
|
(5.5) |
где
,
и
– координаты соответственно точек
,
и
,
следовательно,
,
.
Ответ:
– центр тяжести треугольника
.
ж) Пусть
– ортоцентр треугольника
.
Найдем координаты точки
как координаты точки пересечения высот
треугольника. Уравнение высоты
было найдено в пункте б).
Найдем уравнение высоты
:
,
,
,
.
Поскольку
,
то решение системы
является координатами
точки
,
откуда находим

Ответ:
– ортоцентр треугольника
.
Задача 5.2.
Фиксированные издержки на предприятии
при выпуске некоторой продукции
составляют F
руб. в месяц, переменные издержки – V0
руб. за
единицу продукции, при этом выручка
составляет R0
руб. за единицу изготовленной продукции.
Составить функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
.
Пример 5.2
Фиксированные
издержки на предприятии при выпуске
некоторой продукции составляют
руб. в месяц, переменные издержки –
руб. за единицу
продукции, при этом выручка составляет
руб. за единицу
изготовленной продукции. Составить
функцию прибыли P(q)
(q
– количество произведенной продукции);
построить ее график и определить точку
безубыточности.
Решение
Вычислим совокупные
издержки на производстве при выпуске
q
единиц некоторой продукции
.
Если будет продано
q
единиц продукции, то совокупный доход
составит
.
Исходя из полученных
функций совокупного дохода и совокупных
издержек, найдем функцию прибыли
,
,
.
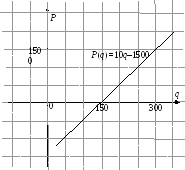
безубыточности – точка, в которой
прибыль равна нулю, или точка, в которой
совокупные издержки равны совокупному
доходу
,
,
откуда находим
– точка безубыточности.
Для построения
графика (рис. 10) функции прибыли найдем
еще одну точку
.
Рис. 10
Ответ:
функция прибыли
,
точка безубыточности
.
Задача 5.3. Законы
спроса и предложения на некоторый товар
соответственно определяются уравнениями
p=pD(q),
p=pS(q),
где p
– цена на товар, q
– количество товара. Предполагается,
что спрос определяется только ценой
товара на рынке pС,
а предложение – только ценой pS,
получаемой поставщиками. Необходимо
а) определить
точку рыночного равновесия;
б) точку равновесия
после введения налога, равного t.
Определить увеличение цены и уменьшение
равновесного объема продаж;
в) найти субсидию
s,
которая приведет к увеличению объема
продаж на q0
ед. относительно изначального
(определенного в пункте а));
г) найти новую
точку равновесия и доход правительства
при введении налога, пропорционального
цене и равного N%;
д) определить,
сколько денег будет израсходовано
правительством на скупку излишка при
установлении минимальной цены, равной
p0.
К каждому пункту
решения сделать рисунок в системе
координат. На рисунке обозначить
соответствующие пункту задачи линии и
точки.
Данные к условию
задачи, соответствующие вариантам:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

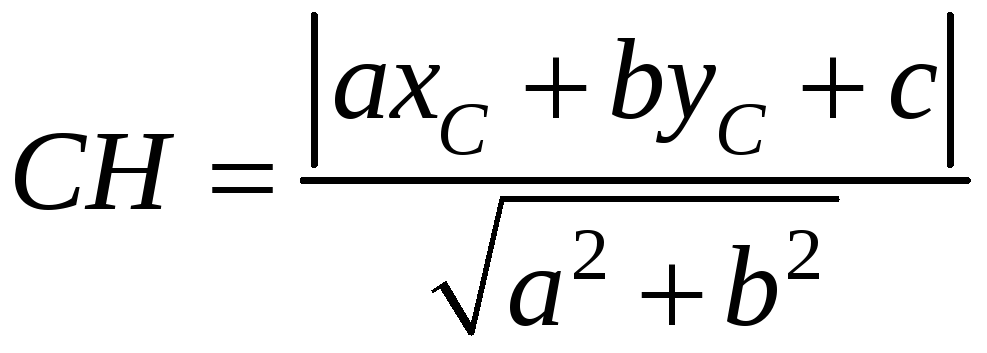 ,
, ис.
ис.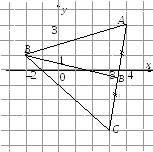 ис.
ис.