Как найти длину высоты в треугольнике вектор

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Как найти длину высоты в треугольнике с вершинами вектора

Как найти высоту зная векторы

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Как найти высоту зная векторы

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

Как найти высоту пирамиды по векторам

Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x₂ – x₁; Y = y₂ – y₁; Z = z₂ – z₁
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:

Пример №2 . В тетраэдре ABCD вычислить:

1. объем тетраэдра ABCD;
2. высоту тетраэдра, опущенную из вершины D на грань ABC.

A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)

Ответ

Проверено экспертом

Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .

Находим векторы АВ, АС и АД.

Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.

Определяем векторное произведение АВ х АС.

-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).

Далее находим смешанное произведение (АВ х АС) х АД.

(АВ х АС) = (-5; -10; 0),

(АВ х АС) х АД = 30 + 10 + 0 = 40.

Объем пирамиды равен (1/6) этого произведения:

V = (1/6)*40 = (20/3) куб.ед.

Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).

Площадь основания АВС равна половине модуля векторного произведения АВ х АС.

S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.

h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

Высота, проведенная к стороне АС, перпендикулярна к стороне АС по определению. Значит вектор высоты, обозначим его Х (х1,х2), должен быть перпендикулярным к вектору АС.

В качестве вектора высоты Х можно взять вектор
Х (с2-а2, -с1+а1). Чтобы проверить, что этот вектор перпендикулярен к вектору АС, надо посчитать скалярное произведение.
Получаем:
(с1-а1)*(с2-а2) + (с2-а2)*(-с1+а1) = 0
Раз скалярное произведение равно нулю, значит векторы перпендикулярны, что нам и нужно.

вектор a(2, -1, 1) вектор b (0, 4, 1)

задан 27 Янв ’14 18:40

Длины векторов легко находятся. Далее через скалярное произведение выражаем косинус угла. Зная косинус, находим синус. Через синус и длины выражаем площадь. Длина разности векторов — это противолежащая сторона. Поделив на неё удвоенную площадь, находим длину высоты.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

1) Зная координаты вершин Можем узнать координаты вектора BC (2-3; -3-1) = BC(-1; -4)

Прямая проходящая через точку A должна идти коллинеарно вектору BC, то есть

(х-0) = k•(-1)

(y-4) = k•(-4)

откуда получаем -х=k и -y/4 +1 = k, приравниваем k

-x = -y/4 + 1 или

4x – y = -4

2) Медиана треугольника приходит в середину противоположной стороны. То есть в точку М – середина AС. Её координаты х = (0+2)/2 = 1; y = (4+(-3))/2 = 0,5; M(1; 0,5)

Получаем медиана идет из точки B в направлении вектора MB (3-1; 1-0,5) = MB (2; 0,5)

Получаем (x-3)/2 = (y-1)/0,5

0,5х – 1,5 = 2y – 2

x – 4y = -1

3) Высота из вершины С перпендикулярна стороне AB. То есть Вектора AB и CH ортогональны и их скалярное произведение = 0

AB (3-0; 1-4) = AB(3; -3)

CH (x-2; y-(-3))

<AB•СH> = 3•(х-2) + (-3)•(y+3) = 0

3x-6 – 3y – 9 = 0

x-y = 5 – получили уравнение прямой высоты CH

Уравнение прямой AB: (х-0)/3 = (y-4)/(-3)

x+y = 4

Точка Н – пересечение этих двух прямых:

Решая систему уравнений подстановкой, находим х=4,5; y=-0,5

CH (4,5-2; -0,5+3) = CH(2,5; 2,5)

|CH| = √(2,5² + 2,5²) = 2,5•√2

Ответ:

1) 4x – y = -4;

2) x – 4y = -1;

3) 2,5•√2

Если известны
координаты точек
и,
то координаты вектора

Разложение этого
вектора по ортам
:

Длина вектора
находится по формуле
а направляющие косинусы равныОрт вектора

Пример 8. Даны
точки

Разложить
вектор
по ортами найти его длину, направляющие косинусы,
орт вектора.
Найдем координаты векторов:

и

Вектор

Контрольные
варианты к задаче 8. Даны
точки А, В и С. Разложить вектор
по ортамНайти длину, направляющие косинусы и
орт вектора.

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Задача 9.
Если даны
векторы
то.

Тогда;
проекция векторана направление вектора,
условие перпендикулярности ненулевых
векторов выглядит следующим образом:

Условие
коллинеарности векторов:
.

Пример 9.
Даны вершины треугольника
Найти угол при вершине А и проекцию
векторана сторону АС. С

Внутренний
угол при вершине А образован векторами,

А
В

Тогда

Проекция
на направление вектора:

Контрольные варианты к задаче 9

1. Даны векторы

иНайти

2. Найти косинус
угла, образованного вектором
и осьюOZ.

3. Даны векторы
и .Найти косинус угла
между диагоналями параллелограмма,
построенного на векторах
.

4. Даны векторы
и
.
Вычислить

5. Найти косинус
угла, образованного вектором и осью ОУ.

6. Даны векторы
и .Найти косинус
угла, образованного вектором
и осью ОХ.

7. Даны векторы
и .Найти

8. Вычислить
проекцию вектора на ось вектора
.

9. Определить
угол между диагоналями параллелограмма,
построенного на векторах и .

10. Определить,
при каком значении m
векторы
иперпендикулярны.

11. Определить,
при каком значении
векторы
и
взаимно перпендикулярны.

12. Даны вершины
треугольника:
.
Определить внутренний угол при вершине
В.

13. Даны вершины
треугольника:
.
Определить внутренний угол при вершине
А.

14. Найти вектор

,
коллинеарный векторуи удовлетворяющий условию

15. Даны две
точки
иВычислить проекцию вектора на ось вектора

16. Даны векторы:
и .
Вычислить

17. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
, .

18. Даны три
вектора:
,,.
Найти

19. Даны три
вектора:
,,.
Найти

20. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
и

21. Даны три
вектора:
,,.
Вычислить

22. Найти вектор
,
зная, что он перпендикулярен векторами

и удовлетворяет
условию

23. Найти вектор

,
коллинеарный векторуи удовлетворяющий условию

24. Даны вершины
треугольника:
Определить внешний угол при вершине А.

25. Даны вершины
треугольника:
Определить внешний угол при вершине А.

26. Дан вектор
и точкииНайти

27. В треугольнике
с вершинами

Определить внутренний угол при вершине
А.

28. Даны векторы

иНайти проекцию векторана направление вектора

29. Даны вершины
треугольника:
Найти проекцию векторана сторону

30. Даны векторы

Найти проекцию вектора
на вектор

Задача 10.
Площадь
параллелограмма, построенного на
векторах

можно найти по
формуле
а площадь треугольника, построенного

на этих векторах:

Пример 10.
Даны вершины треугольника
Найти его площадь и длину высоты,
опущенной из вершины С.

.
Находим векторы

Векторное
произведение

Так как
гдедлина
высоты, опущенной из вершины С на сторону
АВ,.

Контрольные
варианты к задаче 10

1. В параллелограмме
ABCD
даны векторы
иНайти площадь параллелограмма,
построенного на диагоналях параллелограмма

ABCD.

2. Даны три
вершины параллелограмма
,,. Найти длину
высоты, опущенной из вершины С
(через площадь

параллелограмма).

3. Найти площадь
треугольника с вершинами
,
,

(средствами
векторной алгебры).

4. Найти площадь
треугольника с вершинами
,
,(средствами
векторной алгебры).

5. Даны три
вершины треугольника:
,,. Найти его высоту,
приняв ВС за основание (через площадь
треугольника).

6. На векторах

ипостроен параллелограмм. Найти

площадь
параллелограмма, сторонами которого
являются диагонали данного параллелограмма.

7. Даны векторы

и.
Найти векторперпендикулярный к векторамесли
модуль векторачисленно равен площади треугольника,
построенного на векторахи тройка векторовлевая.

8. Даны точки
,,
Найти площадь параллелограмма,
построенного на векторах
и ().

9. На векторах

ипостроен параллелограмм. Найти высоту,
опущенную на основание(через
площадь).

10. В треугольнике
ABC,
где
,найти
длину высоты, опущенной на сторонуAB
(через площадь треугольника; средствами
векторной алгебры).

11. На векторах

ипостроен параллелограмм. Найти площадь
параллелограмма, построенного на
диагоналях данного параллелограмма.

12. В треугольнике
с вершинами
, и точка E
делит сторону АВ пополам. Найти площадь
треугольника АСЕ (средствами векторной
алгебры).

13. Найти площадь
параллелограмма со сторонами
если

14. Найти площадь
треугольника со сторонами
если,

и

15. Дан треугольник
с вершинами
, и .
Вычислить площадь треугольника и
высоту, опущенную из вершины А (средствами
векторной алгебры).

16. Даны векторы

иНайти вектор,
который пер-

пендикулярен
векторам
,
если длина его численно равна площади
треуго-

льника, построенного
на векторах
,
и тройка векторовправая.

17. Даны точки

,и .
Вычислить площадь треугольника и
высоту, опущенную из вершины С (средствами
векторной алгебры).

18. В треугольнике
с вершинами
, и точка E
делит сторону АВ пополам. Найти площадь
треугольника ВСЕ (средствами векторной
алгебры).

19. Даны точки

,и .
Найти площадь параллелограмма,
построенного на векторах
и

20. Даны три
вершины треугольника:
,,.
Вычислить его высоту, опущенную из
вершины В (через площадь, средствами
векторной алгебры).

21. Дан треугольник
с вершинами
, и .
Найти его высоту, опущенную из вершины
А (через площадь, средствами векторной
алгебры).

22. Даны векторы

иВычислить площадь треугольника,
построенного на векторах

23. Даны векторы

иВычислить площадь треугольника,
построенного на векторах

24. Найти площадь
параллелограмма, построенного на
векторах
где

25. В треугольнике
с вершинами
, и точка E
делит сторону АВ пополам. Найти площадь
треугольника АСЕ (средствами векторной
алгебры).

26. Даны векторы

иНайти вектор,
который перпендикулярен векторамесли модуль векторачисленно равен площади треугольника,
построенного на векторах,
и тройка векторовлевая.

27. Даны точки

, и .
Найти длину высоты треугольника АВС,
опущенной из вершины С (через площадь,
средствами векторной алгебры).

28. Даны три
вершины параллелограмма
,и.
Найти длину высоты, опущенной из вершины
С (через площадь, средствами векторной
алгебры).

29. На векторах

ипостроен параллелограмм. Найти площадь
параллелограмма, построенного на его
диагоналях.

30. Даны векторы

,иВычислить площадь треугольника,
построенного на векторах

Задача 11.
Если даны координаты
,
то смешанное произведение векторов
вычисляют по формуле

.

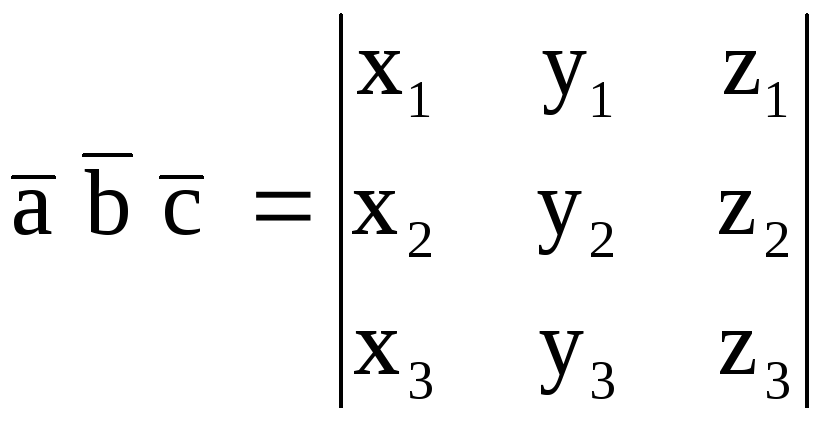
Объемы
параллелепипеда и тетраэдра (треугольной
пирамиды), построенных на векторах
находятся с помощью смешанного
произведения векторов:

,

Если > 0, то тройка
векторов – правая.

Если < 0, то тройка
левая.

Если = 0, то векторы
компланарны.

Пример 11.
Дан параллелепипед
построенный на векторахиНайти
высоту, проведенную из вершинына граньABCD.

Объем

равен произведению площади основания
на высоту:

находится также
по формуле
,
поэтому

.

Вычислим
векторное произведение
=

Тогда

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #