Формула длины хорды окружности
Хорда – отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L – хорда
R – радиус окружности
O – центр окружности
α – центральный угол
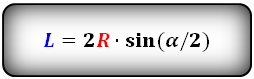
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021
Как посчитать хорду окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать хорду окружности
Чтобы посчитать хорду круга (окружности) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
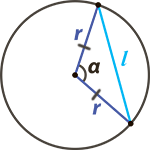
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
угол α °
Ответ:
0
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
угол α рад
Ответ:
0
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
l = 2r⋅sinα/2
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
См. также
Окружность – это фигура на плоскости, все точки которой равноудалены от центра окружности. Окружность
– самая простая фигура, которую можно провести на местности, для этого достаточно колышка для
обозначения центра окружности и веревки с чертилкой. Чтобы вычертить окружность на листе бумаги,
достаточно циркуля.
Хорда – это отрезок, соединяющий 2 любые точки окружности. Самой длинной хордой является диаметр, или
согласно другому определению, диаметр – это хорда, проходящая через центр окружности. Нередко
появляется практическая необходимость рассчитать длину хорды по известному радиусу окружности и
одному из 2 углов, определяющих положение хорды (центральному или вписанному). В окружности
центральный угол – это угол, вершина которого располагается в центре окружности, а вписанный угол –
это угол, вершина которого лежит на окружности. Или же, вписанный угол — это угол,
образованный двумя пересекающимися на окружности хордами.
- Длина хорды через радиус и угол между радиусами
- Длина хорды через вписанный угол и радиус
Через радиус и угол между радиусами
Если известен радиус и угол между радиусами, то формула будет следующая:
L = 2R * sin α/2
где R – радиус окружности, α – центральный угол между радиусами, опирающийся на хорду.
Цифр после
запятой:
Результат в:
Пример. Решим практическую задачу: на местности строится из кирпича сооружение, в
плане имеющее форму неполной окружности с радиусом 3 м, со стороны входа стянутой хордой, на которую
опирается центральный угол в 36°. Найти длину хорды, что требуется для построения на местности без
откладывания угла, а также проверки, достаточно ли в прямой стенке места для входа и устройства
двери. L = 2R * sin α/2 = 2 * 3 * sin 36°/2 = 6 * 0,309 = 1,854 (м).
Через вписанный угол и радиус
Если известен вписанный угол и радиус, то формула по нахождению длины хорды следующая:
L = 2R * sin α
где R — радиус, sin α — вписанный угол
Цифр после
запятой:
Результат в:
Удивительно простой вид этой формулы основан на теореме о вписанном угле, согласно которой вписанный
угол равен половине центрального угла, опирающегося на ту же дугу (а соответственно на ту же хорду),
тем самым данная формула выводится из предыдущей.
Пример. В качестве примера, рассчитаем длину хорды в окружности радиусом 10 м, на
которую опирается вписанный угол 30°. L = 2R * sin α = 2 * 10 * sin 30° = 20 * 0,5 = 10 (м).
Длина хорды оказалась равной радиусу, т.е. представляет собой одну сторону вписанного в окружность
шестиугольника.
Таким образом, расчет длины хорды позволяет построить на местности или бумаге любой правильный
многоугольник без необходимости откладывания углов, центральных или вписанных. Уже в эпоху
первобытного строя люди знали о свойствах окружности, и пользовались ими для своих целей. Одно из
самых известных сооружений той поры – Стоунхендж в Англии, предположительно являвшийся
астрономической обсерваторией. Следовательно, уже тогда появилась необходимость выдерживать строго
центральные и вписанные углы.
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Хорда – отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
Определение хорды
Хорда – это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности
Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .
Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой – с другой стороны.
Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности – самая длинная хорда окружности.
Свойства хорды к окружности
- Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное – если хорды равны, то расстояния от центра окружности до этих хорд равны
- Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
- Наибольшая возможная хорда является диаметром
- Серединный перпендикуляр к хорде проходит через центр окружности
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное – если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
- Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное – если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное – если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
- Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное – если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
- Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное – если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.
Свойства хорды и вписанного угла
Свойства хорды и центрального угла
Формулы нахождения хорды
Обозначения в формулах:
l – длина хорды
α – величина центрального угла
R – радиус окружности
d – длина перпендикуляра, проведенного от центра окружности к хорде
Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.
Решение задач
Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.
Задача.
Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.
Решение.
Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x
Согласно свойству хорд AS x SB = CS x SD, тогда
2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10
Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10
Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.
Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
Поскольку градусная мера окружности равна 360 градусам, то
3,5х + 5,5х + 3х = 360
12х = 360
х = 30
Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
[spoiler title=”источники:”]
http://www-formula.ru/circle-chord-l
http://profmeter.com.ua/communication/learning/course/course7/lesson318/
[/spoiler]
Длина хорды окружности
В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром.
Определение длины хорды окружности
Формула расчёта длинны хорды
Длина хорды окружности может быть определена по формуле:
L = 2r × sin ( α / 2 )
L – хорда
r – радиус окружности
O – центр окружности
α – центральный угол
Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения.
Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты. Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий.
Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды. При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника.
Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры).