Как находить длину
Длиной принято обозначать расстояние между двумя точками какого-либо отрезка. Это может быть прямая, ломаная или замкнутая линия. Вычислить длину можно довольно простым путем, если знать некоторые другие показатели отрезка.

Инструкция
Если вам нужно найти длину стороны квадрата, то это не составит труда, если вам известна его площадь S. В связи с тем, что все стороны квадрата имеют одинаковую длину, вычислить величину одной из них можно по формуле: a = √S.
В случае, когда требуется просчитать длину стороны прямоугольника, воспользуйтесь значениями его площади s и длины другой стороны b. Из формулы a=S/b вы получите искомое значение.
Чтобы определить длину окружности, то есть замкнутой линии, которая образует круг, воспользуйтесь значениями: r – ее радиусом и D – диаметром. Диаметр можно вычислить, умножив радиус окружности на 2. Известные вам значения подставьте в формулу определения длины окружности: C=2πr=πD, где π=3,14.
Для вычисления длины обычного отрезка воспользуйтесь методом эксперимента. То есть возьмите линейку и измеряйте.
Для того чтобы вычислить длину стороны такой фигуры, как треугольник, вам понадобятся размеры двух других сторон, а также величины углов. Если вы имеете дело с прямоугольным треугольником, и один из его углов равен 60 градусам, то величину его катета можно определить по формуле a=c*cosα, где c – гипотенуза треугольника, а α – угол между гипотенузой и катетом.
Помимо этого, если вы располагаете такими известными величинами, как высота b и площадь S треугольника, то длину стороны, которая является основанием, можно узнать благодаря формуле a=2√S/√√b.
Что касается правильного многоугольника, то длину его стороны можно просчитать, руководствуясь формулой an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности, n – количество углов.
Если вы хотите вычислить длину равносторонней фигуры, вокруг которой описана окружность, то сделать это можно по формуле an=R√3, где R – радиус окружности, n – количество углов фигуры.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как вычислить длину
Длина характеризует расстояние между начальной и конечной точками отрезка. Различают длину прямой, ломаной и замкнутой линий. Ее находят экспериментальным либо аналитическим способом.

Инструкция
Термин «длина» у большинства людей ассоциируется с соответствующей характеристикой прямой линии. Однако на самом деле, этот параметр имеется у линии любой формы. Так, например, она имеется у окружности.
Окружность представляет собой замкнутый отрезок, который является образующей круга. Если точно следовать определению, то окружностью называется геометрическое место точек плоскости, равноудаленных от ее центра. Все окружности имеют некоторый радиус, обозначаемый как r, а также диаметр, равный D=2r. Длина этой линии равна значению выражения:C=2πr=πD, где r – радиус окружности, D – диаметр окружности.
Если речь идет о прямой линии, то имеется в виду либо обычный отрезок, либо замкнутая фигура, такая как треугольник или прямоугольник. Для последнего длина является основной характеристикой. Простой отрезок можно измерить экспериментально, а длину стороны у фигуры удобнее всего вычислить. Наиболее просто осуществить эту операцию в отношении прямоугольника.
Частным случаем прямоугольника является равносторонний, называемый квадратом. В условиях некоторых задач приведено только значение площади, а найти необходимо сторону. Поскольку стороны квадрата равны, то она вычисляется по следующей формуле:a = √S.Если прямоугольник не равносторонний, то, зная его площадь и одну из сторон, найдите длину перпендикулярной стороны следующим образом:a=S/b, где S – площадь прямоугольника, b – ширина прямоугольника.
Длина стороны треугольника находится несколько иным способом. Для определения этой величины необходимо знать не только длины остальных сторон, но и значения углов. Если дан прямоугольный треугольник с углом 60° и стороной с, которая является его гипотенузой, длину катета найдите по следующей формуле:a=c*cosα.Кроме того, если в задаче дана площадь треугольника и высота, длину основания можно найти по другой формуле:a=2√S/√√3.
Длину сторон любой фигуры проще всего найти, если она равносторонняя. Например, если вокруг равностороннего треугольника описана окружность, длину стороны этого треугольника вычислите следующим образом:a3=R√3.Для произвольного правильного n-угольника сторону найдите следующим образом:an=2R*sin(α/2)=2r*tg(α/2), где R – радиус описанной окружности, r – радиус вписанной окружности.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Длина отрезка
Отрезок – это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.
Измерить отрезок – значит найти его длину (расстояние между его концами).
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.
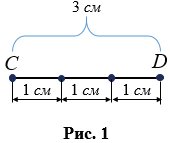
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).
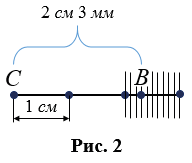
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
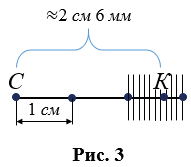
- Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Длина отрезка – это всегда какое-то положительное число.
Свойства длин отрезков:
- Равные отрезки имеют равные длины.
- Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.
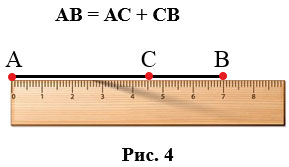
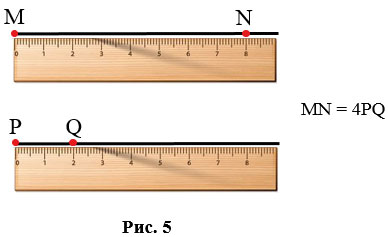
- Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 29,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 31,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 33,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 37,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 39,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 74,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 79,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Сторона геометрической фигуры – это отрезок, соединяющий вершины фигуры. Равенство сторон или наличие прямых углов, соединяющих их, дает определенные свойства фигуре, благодаря которым становится возможным узнать другие измерительные величины. Поскольку определенное количество известных измерений, в том числе и сторон, определяет существование в плоскости одной, и только одной подобной фигуры, это позволяет также построить данную фигуру в плоскости.
В данном разделе можно найти все необходимые формулы и их доказательства для расчетов сторон любой геометрической фигуры, а также воспользоваться онлайн калькуляторами.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Как найти длину?
Закон синусов гласит, что для всех углов треугольника отношение синуса этого угла к его противоположной стороне всегда будет одинаковым. В длина стороны c — 2.98. Закон косинусов гласит, что вы можете определить длину любой стороны треугольника, если вы знаете противоположный угол и длины двух других сторон.
Что такое формула длины?
Для круга формула длины дуги равна θ, умноженному на радиус круга. Формула длины дуги в радианах может быть выражена как, длина дуги = θ × r, когда θ в радианах. Длина дуги = θ × (π / 180) × r, где θ в градусах, где L = длина дуги.
Также нужно знать, какова длина AB? если два угла имеют равные меры, то противоположные им стороны равны по длине. Таким образом, длина стороны AB равна 6 единиц.
Соответствует ли длина цилиндра высоте?
Высота цилиндра такой же длины, как и окружность его основания. Его измеренная высота — 125.66 см.
Как определить длину одной стороны треугольника?
Чтобы собрать треугольник с одной стороной, вам также понадобится один из непрямых углов. В противном случае это невозможно: если у вас есть гипотенуза, умножьте его на sin (θ) чтобы получить длину стороны, противоположной углу. Или же умножьте гипотенузу на cos (θ), чтобы получить сторону, примыкающую к углу.
Каково правило длины сторон треугольника?
Правило сторон треугольника утверждает, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. См. Длины сторон острого треугольника ниже. Сумма длин двух самых коротких сторон, 6 и 7, равна 13.
Какова формула периметра?
Периметр, площадь и объем
| Таблица 1 . Формулы периметра | ||
|---|---|---|
| Форма | Формула | Переменные |
| Квадратный | P= 4s |
s — длина стороны квадрата. |
| Прямоугольные | P = 2L + 2W | L и W — длины сторон прямоугольника (длина и ширина). |
| Треугольник | а + б + с | a, b и c — длины сторон. |
Какая формула высоты?
Рассчитайте высоту интересующего объекта, вычислив «Д * загар (тета), », Где« * »означает умножение, а« tan »- тангенс угла тета. Например, если тета равна 50 градусам, а D — 40 метров, то после округления высота составляет 40 тангенциальных 50 = 47.7 метра.
Длина длинной ножки прямоугольного треугольника?
гипотенуза всегда находится напротив прямого угла и всегда является самой длинной стороной треугольника. Чтобы найти длину участка a, подставьте известные значения в теорему Пифагора. … Вы знаете, что в этом треугольнике гипотенуза (сторона, противоположная прямому углу) имеет длину 10.
По какой формуле вычисляется длина AB?
ПС = 2 + 3 = 5 см. SR = 3 — 2 = 1 см. ∆ OQP — прямоугольный треугольник. AB = 7.35 см.
Какая сторона XYZ самая длинная?
Ответ: XY — самая длинная сторона в заданном ΔXYZ.
Какая сторона ABC самая длинная?
Поскольку угол A, угол B и угол C являются противоположными углами сторон BC, CA и AB соответственно ⇒ BC> CA> AB. Следовательно, самая длинная сторона треугольника ABC равна BC.
Какая высота цилиндра?
Высота h цилиндра равна расстояние между двумя базами. Для всех цилиндров, с которыми мы будем работать здесь, стороны и высота h будут перпендикулярны основанию. Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.
Какая формула цилиндра?
Формула объема цилиндра: V = Bh или V = πr2h . Радиус цилиндра 8 см, высота 15 см. … Следовательно, объем цилиндра составляет порядка 3016 кубических сантиметров.
Как найти угол с двухсторонним калькулятором?
- Шаг 1 Нам известны две стороны: Соседняя (6,750) и Гипотенуза (8,100).
- Шаг 2 SOHCAHTOA сообщает нам, что мы должны использовать косинус.
- Шаг 3 Вычислить смежное значение / гипотенуза = 6,750 / 8,100 = 0.8333.
- Шаг 4 Найдите угол на вашем калькуляторе, используя cos
–
1
0.8333:
Как найти длину третьей стороны треугольника?
Теорема о неравенстве треугольника утверждает, что сумма любых двух сторон треугольника должна быть больше, чем размер третьей стороны.
- Итак, разница двух сторон
- Следовательно, 9−3
- 6
Какова длина треугольника 45 45 90?
Треугольник 45 ° -45 ° -90 ° — это специальный прямоугольный треугольник, который имеет два угла 45 градусов и один угол 90 градусов. Длины сторон этого треугольника пропорциональны; Боковая сторона 1: Сторона 2: Гипотенуза = n: n: n√2 = 1: 1: √2. Прямоугольный треугольник 45 ° -45 ° -90 ° составляет половину квадрата.
Что такое формула массы?
Масса тела всегда постоянна. Один из способов вычисления массы: Масса = объем × плотность. Вес — это мера силы тяжести, действующей на массу.
Какова формула максимальной высоты?
Максимальная высота h, достигаемая снарядом, равна половине H, высоты этого треугольника. = H — ½H, поэтому h = H / 2, что и является желаемым результатом.
Как найти начальную высоту?
Начальная скорость, v0 = 200 фут / сек, а начальная высота h0 = 0 (поскольку запускается с земли). Формула: h = -16t 2 + 200т + 0.
Каково уравнение максимальной высоты?
Максимальная высота объекта с учетом начального угла запуска и начальной скорости определяется с помощью:h = v2isin2θi2g h = vi 2 sin 2 θ я 2 г.
Какова длина одной ножки треугольника?
Длина одной ноги составляет 22 единиц.
Всегда ли сторона A длиннее стороны B в прямоугольном треугольнике?
2 ответа. Сторона A и B не имеет значения, когда вы пытаетесь применить это к теореме Пифагора, но сторона C всегда должна быть гипотенуза. Гипотенуза — всегда самая длинная сторона треугольника. Он противоположен прямому углу.
Как найти длину третьей стороны треугольника?
Теорема Пифагора для третьей стороны прямоугольного треугольника. Теорема Пифагора используется для определения длины гипотенузы прямоугольного треугольника. Итак, если вам даны две длины, вы можете использовать алгебру и квадратные корни, чтобы найти длину недостающей стороны.
КАК НАЙТИ ДЛИНУ ЕСЛИ ИЗВЕСТНО ШИРИНА ВЫСОТА ОБЪЕМ? КАК НАЙТИ ШИРИНУ ЕСЛИ ИЗВЕСТНО ДЛИНА ВЫСОТА ОБЪЕМ?
КАК НАЙТИ ВЫСОТУ ЕСЛИ ИЗВЕСТНО ДЛИНА ШИРИНА ОБЪЕМ?
КАК НАЙТИ ОБЪЕМ ЕСЛИ ИЗВЕСТНО ДЛИНА ШИРИНА ВЫСОТА?
ПОЖАЛУЙСТА ПОИОГИТЕ СРОЧНО НАДО.

Если дан прямоугольный параллелепипед, то объем можно найти, перемножив его длину, ширину и высоту.
Пусть длина а, ширина b, высота с, объем V.
Отсюда следует, что:

Объём есть произведение длины, высоты и ширины.
Чтобы найти одно измерение, нужно найти произведение двух других и разделить объем на это число.
Длина окружности

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности: 
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен  Подставим туда наши переменные и получим
Подставим туда наши переменные и получим 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
