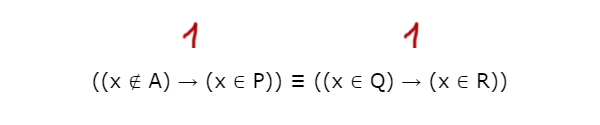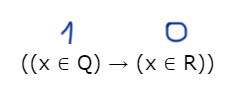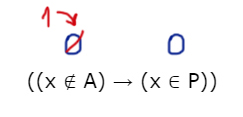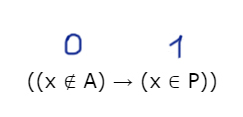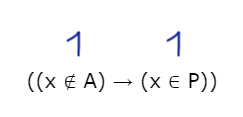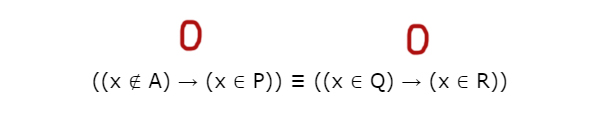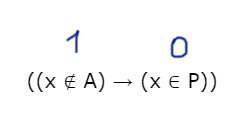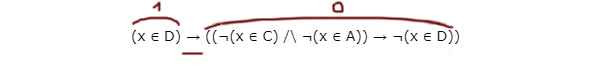I want to calculate the length of (any number of) line segments using Python. I used the following code, but I encounter that tuples can not have subtraction as operands. How can I overcome that? I would like to know if I missed any important Python concept.
from itertools import starmap
import math
class Point(object):
def __init__(self,x,y):
self.x=x
self.y=y
def move(self,dx,dy):
self.x+=dx
self.y+=dy
class LineString(object):
def __init__(self,*args): # A method with any number of arguments, args
self.args=[Point(*args) for p in args] # A list of Points
def length(self):
pairs=zip(self.args, self.args[1:])
return sum(starmap(distance,pairs))
def distance(p1, p2):
a = p1.x,p1.y
b = p2.x,p2.y
print (math.sqrt((a[0]-b[0])**2-(a[1]-b[1])**2))
# calculates distance between two given points p1 and p2
return math.sqrt((a** 2)+ (b** 2))
if __name__ == '__main__':
# Tests for LineString
# ===================================
lin1 = LineString((1, 1), (0, 2))
assert lin1.length() == sqrt(2.0)
lin1.move(-1, -1) # Move by -1 and -1 for x and y respectively
assert lin1[0].y == 0 # Inspect the y value of the start point.
# Implement this by overloading __getitem__(self, key) in your class.
lin2 = LineString((1, 1), (1, 2), (2, 2))
assert lin2.length() == 2.0
lin2.move(-1, -1) # Move by -1 and -1 for x and y respectively
assert lin2.length() == 2.0
assert lin2[-1].x == 1 # Inspect the x value of the end point.
print ('Success! Line tests passed!')
Напишите программу, которая вычисляет длину отрезка (т.е. расстояние между двумя точками), заданного двумя значениями x1 и x2 (вещественные числа).
## Длина отрезка по координатам его концов рассчитывается по формуле d = √ (x2-x1)²+ (y2-y1)²), где d — рассчитываемый отрезок, x1, x2 — абсциссы начала и конца отрезка, y1, y2 — ординаты начала и конца отрезка.
Верное решение:
x1, x2 = float(input()), float(input())
print(abs(x2 – x1))
Верное решение:
x1, x2 = map(float,input().split())
d=abs(x1 – x2)
print(d)
Верное решение:
x1, x2 = map(float, input().split())
print(abs(x2 – x1))
Верное решение:
a, b = float(input()), float(input())
print(abs((max(a, b)) – min(a, b)))
Верное решение (в одну строку):
print(abs(float(input())-float(input())))
Верное решение (разминка перед ЕГЭ):
a, b = [float(i) for i in input().split()]
print(abs(a – b))
Python является кроссплатформенным. То есть программа, написанная на Windows, легко запустится на Linux или MacOs.
Skip to content
Задача «Длина отрезка»
Условие
Даны четыре действительных числа: x1, y1, x2, y2. Напишите функцию distance(x1, y1, x2, y2), вычисляющая расстояние между точкой (x1,y1) и (x2,y2). Считайте четыре действительных числа и выведите результат работы этой функции.
Если вы не знаете, как решить эту задачу, то вы, возможно, не изучали в школе теорему Пифагора. Попробуйте прочитать о ней на Википедии.
Решение задачи от разработчиков на Python:
Другая реализация задачи на Python:
Смотреть видео — Задача «Длина отрезка» решение на Python
Делитесь с друзьями ссылкой на ответ и задавайте вопросы в комментариях! 👇
Related Posts
это один из элементов метода самоидентификации фигур с помощью машинного зрения. здесь неплохо бы вспомнить плоскую систему координат Эйлера в смысле ее модификации для решения задачи распознавания фигур по их границам вне зависимости от их расположения на пиксельной матрице
Длина отрезка
21.12.2016, 19:56. Показов 32007. Ответов 9
Метки нет (Все метки)

Даны четыре действительных числа: x1, y1, x2, y2. Напишите функцию distance(x1, y1, x2, y2), вычисляющая расстояние между точкой (x1,y1) и (x2,y2). Считайте четыре действительных числа и выведите результат работы этой функции.
Входные данные:
0
0
1
1
Выходные данные:
1.41421
Помогите решить, пожалуйста
Добавлено через 58 минут
Еще входные данные:
0
0
1
0
Добавлено через 1 минуту
Выходные данные:
1
1
Привет! Сегодня посмотрим задачи на отрезки из 15 задания ЕГЭ по информатике.
Решим с помощью шаблона на Python и помощью рассуждений. Повторите основные логические операции в этой статье.
Покажу Вам уникальный и понятный способ для борьбы с задачами на отрезки из 15 задания ЕГЭ по информатике.
Приступим к тренировочным задачам на отрезки.
Задача (Fight)
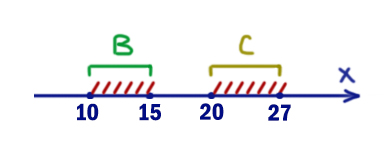
На числовой прямой даны два отрезка B=[10; 15] и С=[20; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(((x ∈ B) ∨ (x ∈ C)) ⟶ (x ∈ A))
ложно (т.е. принимает значение 0) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
Приведу собственную разработку, как можно решить задачи на отрезки из 15 задания ЕГЭ по информатике с помощью шаблона на языке Python (Питон).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i/2 if not( (F(10, 15, x) or F(20, 27, x)) ) or F(a, b, x): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим функцию F(a, b, x). Она принимает три параметра: начало отрезка a, конец отрезка b и точку x. Если точка x лежит в отрезке [a;b], то функция вернёт True, иначе False.
Затем делаем два вложенных цикла. Это поиск отрезка A. Переменная a – это начало отрезка A. Переменная b – это конец отрезка A. Для каждой точки a пробуем различные точки b, которые находится правее, чем точка a. Мы начинаем проходить переменной b со значения a, потому что в некоторых задачах длина искомого отрезка A может быть равна нулю.
Для каждого отрезка-кандидата заводим счётчик k. Прокручиваем переменную i в диапазоне от 1 до 199 включительно. А x будет крутится от 0.5 до 99.5 с шагом 0.5, тем самым имитируя фразу при любых значениях x.
Внутри “цикла i” проверяем логическое выражение. Если выражение удовлетворяет условию задачи, то прибавляем к счётчику k единицу для данного отрезка A=[a; b].
При составлении логического выражения может помочь табличка.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
После окончания “цикла i” проверяем счёт k. Если логическое выражение сработало при всех значениях x, то в счётчике будет число 199. Это количество итераций в “цикле i”. Если такое выполняется, то нам подходит этот отрезок A.
Среди всех отрезков A, которые удовлетворяют условию задачи, выбираем с наименьшей длиной с помощью функции min.
Примечание: У нас всегда получается отрезок A c квадратными скобками на концах A=[a, b]. Даже, если в задачке должен быть отрезок с выколотыми точками, то на длину это никак не влияет, если мы ищем минимальный отрезок, поэтому всё равно будет получатся правильный ответ. Если же мы ищем наибольшую длину, нужно получать всегда отрезок A=(a,b) c выколотыми точками. Об этот речь пойдёт ниже.
Получается 17.
Решение с помощью рассуждений.
Видим, что ко всему выражению применяется логическое отрицание. Мы можем убрать это отрицание, но тогда нужно будет сделать, чтобы выражение было истинным, а не ложным.
В подобных задачах идём от обратного. Нам нужно найти, когда выражение будет истинным, но мы исследуем случай, когда выражение будет стремится ко лжи.
Найдём, при каких значениях x левое выражение будет выдавать 1.
Здесь заштрихованы те иксы, которые приводят к тому, что левое выражение выдаёт 1. Это опасные x. Они “приближают” всё выражение к нулю.
Наша задача этого не допустить. У нас есть только один инструмент: подобрать такой отрезок A, чтобы правое выражение при опасных иксах выдавало 1. Тогда мы получим желаемый результат.
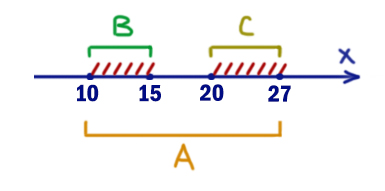
Т.е. при опасных иксах правое выражение должно выдавать 1. Чтобы покрыть все иксы приходится брать отрезок A=[10, 27].
В ответе напишем длину отрезка A: 27 – 10 = 17. Здесь достаточно из наибольшей точки отнять наименьшую.
Ответ: 17
Задача (Раунд 2)
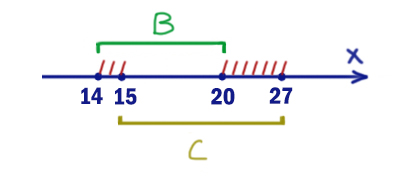
На числовой прямой даны два отрезка: B = [14; 20] и С = [15; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(x ∈ A) ⟶ ((x ∈ B) ≡ (x ∈ C))
истинно (т.е. принимает значение 1) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if F(a, b, x) or (F(14, 20, x) == F(15, 27, x)): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Получается ответ 13.
Решение с помощью рассуждений.
“Главной скрипкой” логического выражение является следование. Именно эта операция соединяет большие блоки логического выражения.
Нас будет интересовать тот случай, когда логическое выражение, наоборот, будет стремится к 0. Тогда правое логическое подвыражение должно равняться 0, а с помощью левого подвыражения, где находится отрезок A, мы будем исправлять ситуацию.
Заштрихуем те значения x, при которых правое подвыражение даёт ноль. Равносильность даёт ноль, когда два выражения имеют разные значения. Т.е. если x находится в одном отрезке, то в другом отрезке его не должно быть.
В подобных задачах можно не обращать внимание на закрашенные и выколотые точки на концах отрезков, потому что в дальнейшем нужно найти длину отрезка A, а длина от этого не зависит. Поэтому пишем и рисуем отрезки с некоторым приближением до одной точки.
Получаются два отрезка [14; 15) и (20; 27]. Это и есть “опасные” значения x. При этих значениях выражение уже “наполовину” ложно. Но с помощью A мы не дадим превратится ему в 0 при любых иксах.
Если левое подвыражение будет равно 1 при опасных значениях икс, то как раз получится то, что нам не нужно. Поэтому при опасных значениях иск, в левом выражении должен быть ноль.
Т.к. там стоит отрицание, убрав его, можно сказать, что в левом подвыражении должна стоять 1 при опасных значениях икс.
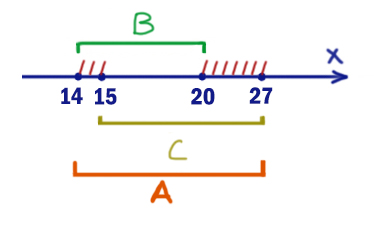
Чтобы покрыть все два отрезка опасных значений, выбираем A=[14; 27]. Нас просили найти минимальный отрезок A. Меньше не можем взять, т.к. тогда не все заштрихованные иксы будут закрыты.
Длина получается 27 – 14 = 13.
Ответ: 13
Задача (Отрезок максимальной длины)
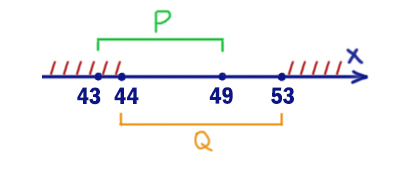
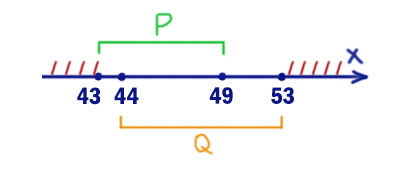
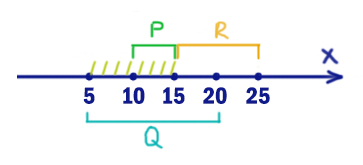
На числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x < b: return True else: return False mx=0 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if (not(F2(a, b, x)) or F(43, 49, x)) or F(44, 53, x): k=k+1 if k==199: mx=max(mx, b-a) print(mx)
Ответ получается 10. Здесь ищем максимальный отрезок A. При поиске отрезка максимальной длины, нужно создать функцию F2, и её применять к отрезку A, чтобы получался всегда отрезок с выколотыми точками A=(a, b).
Решение с помощью рассуждений.
Главная скрипка – это логическое или. Эта логическая операция соединяет два больших выражения.
Идём от обратного. Исследуем, когда выражение будет стремится к 0.
Логическое или выдаёт ноль, когда оба выражения равны нулю.
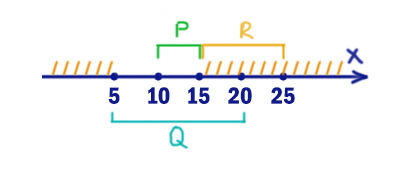
В начале лучше разобраться с тем выражением, где нет отрезка A. Это правое подвыражение. Там должен получаться ноль. Заштрихуем те иксы, которые выдают в правом подвыражении ноль.
В левом выражение стоит следование. Эта операция равна нулю, когда из 1 следует 0. С помощью отрезка A мы будем спасать ситуацию. Заштрихуем, когда икс НЕ принадлежит P. Добавим это действие к предыдущей штриховке.
Таким образом, мы получили опасные иксы. Это все иксы, кроме отрезка [43; 53].
Именно при этих иксах выражение (x ∈ A) не должно выдавать 1. Выбираем отрезок A=[43; 53].
Мы могли бы взять отрезок и меньше, например [44; 49], но нас просили взять наибольший отрезок.
Длина равна 53 – 43 = 10.
Ответ: 10
Задача (Крепкий орешек)
На числовой прямой даны три интервала: P=[10,15], Q=[5,20] и R=(15,25]. Определите наименьшую возможную длину отрезка A, при выборе которого выражение
((x ∉ A) → (x ∈ P)) ≡ ((x ∈ Q) → (x ∈ R))
будет ложно при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not( (F(a, b, x) or F(10, 15, x)) == (not(F(5, 20, x)) or F2(15, 25, x)) ): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим ещё одну функцию F2 для отрезка R с выколотой левой точкой. Ответ получается 5.
Решение с помощью рассуждений.
Нужна ложь, но мы рассмотрим, когда равносильность выдаёт 1.
1) Рассмотрим первый случай 1 ≡ 1.
Рассмотрим левое выражение. Узнаём, когда оно выдаёт ноль, а потом сделаем инверсию, чтобы не рассматривать 3 случая.
Получается, что в отрезке Q иксы должны находится, а в R нет.
Сделаем инверсию.
Получается интервал x ∈ (-∞ 5) U (15; ∞). Это те иксы, при которых в правом выражении будет 1.
Рассмотрим, когда левое выражение выдаёт 1.
a) 0 → 0
Учитывая вышеописанный интервал, понимаем, что иксы и так не лежат в отрезке P. Чтобы спаси ситуацию, нужно, чтобы выражение (x ∉ A) выдавало 1, при x ∈ (-∞ 5) U (15; ∞). Тогда левое выражение будет выдавать 0, а правое 1.
Следовательно, можем выбрать любой отрезок A в интервале [5; 15].
б) 0 → 1
При x ∈ (-∞ 5) U (15; ∞) выражение (x ∈ P) никогда не выдаст 1. Значит, в этом варианте 1 ≡ 1 никогда не будет.
в) 1 → 1
Аналогично невозможна и эта ситуация.
Перейдём ко второму случаю.
2) Рассмотрим случай 0 ≡ 0.
Когда правое выражение выдаёт ноль, мы уже смотрели. Это отрезок [5; 15].
Изучим те значения x, при которых левое выражение тоже будет выдавать 0 на отрезке [5; 15].
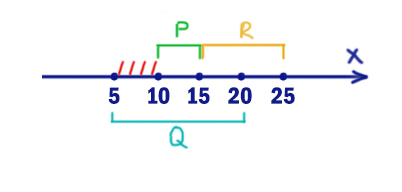
Тогда опасные иксы будут выглядеть следующим образом:
Т.е. это интервал [5; 15], но без отрезка P. Именно при x ∈ [5; 10) мы должны получать 0 в выражении (x ∉ A), чтобы спасти ситуацию. Получается A=[5;10). Меньше взять отрезок не можем, иначе не все опасные иксы будут покрыты.
Этот отрезок хорошо соотносится с первым вариантом 1) 1 ≡ 1.
Ответ получается 10 – 5 = 5.
Ответ: 5
Задача (Вперёд к победе!)
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите
наименьшую возможную длину такого отрезка A, для которого логическое
выражение.
(x ∈ D) → ((¬(x ∈ C) ∧ ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not(F(17, 58, x)) or (not((not(F(29, 80, x)) and not(F(a, b, x)))) or not(F(17, 58, x))): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Решение с помощью рассуждений.
“Главной скрипкой” данного логического выражения является следование, потому что эта операция соединяет различные логические блоки.
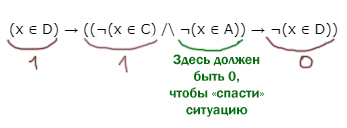
Нам нельзя допустить, чтобы первое выражение принимало 1, а второе 0, одновременно.
Рассмотрим при каких значениях x реализуется этот страшный вариант.
Видно, что, если левое выражение (x ∈ D) равно 1, то ¬(x ∈ D) в правой части автоматически выдаёт 0.
Чтобы умножение в правой части давало 1, необходимо, чтобы выражение ¬(x ∈ C) было истинным.
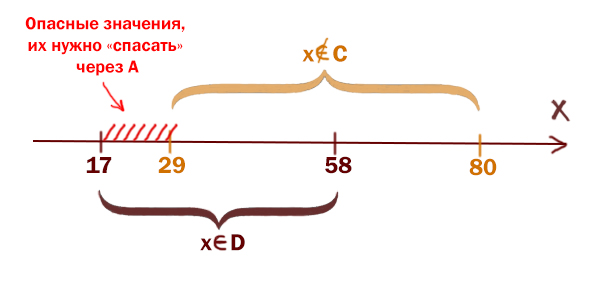
Тогда опасные значения – это отрезок D без отрезка C. Т.е., чтобы иксы были в отрезке D, но не были в отрезке С одновременно.
Опасные значения получаются [17; 29]. Чтобы опасный сценарий нейтрализовать, выражение ¬(x ∈ A) должно принимать значение 0. Тогда (x ∈ A) должно выдавать 1. Чтобы это происходило всегда при опасных значениях, принимаем A=[17, 29]. Длина получается 12.
Ответ: 12
Александр, а вот зачем в первой задаче учитывать вещественные x(я про деление i на 2), ведь если брать x целыми, то ответ не меняется. Это может быть критично в других задачах? И в каких случаях это повлияет на ответ?
Да, ответ может совпадать, но, например, в задаче “Крепкий орешек”, из этой статьи, уже целыми числами не обойтись