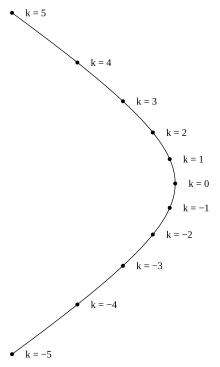
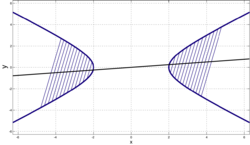
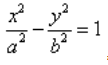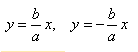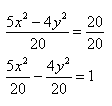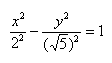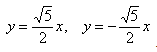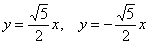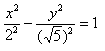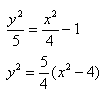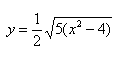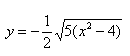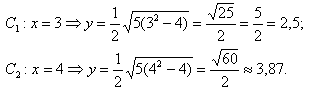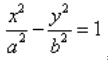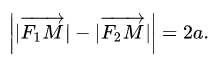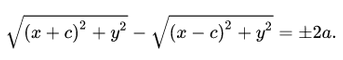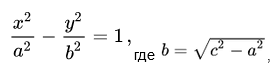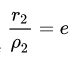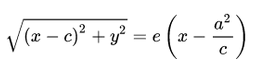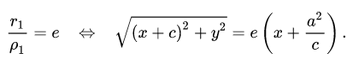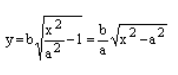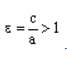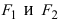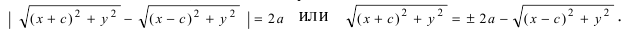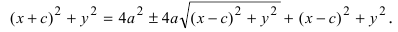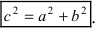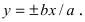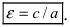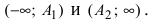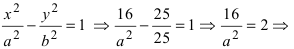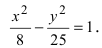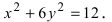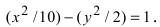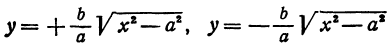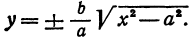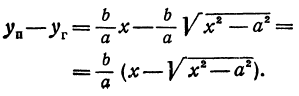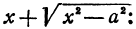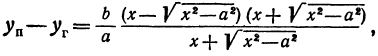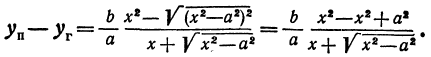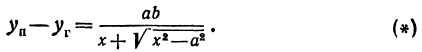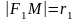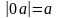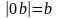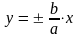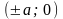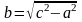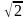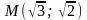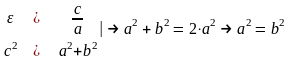Что такое гипербола
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
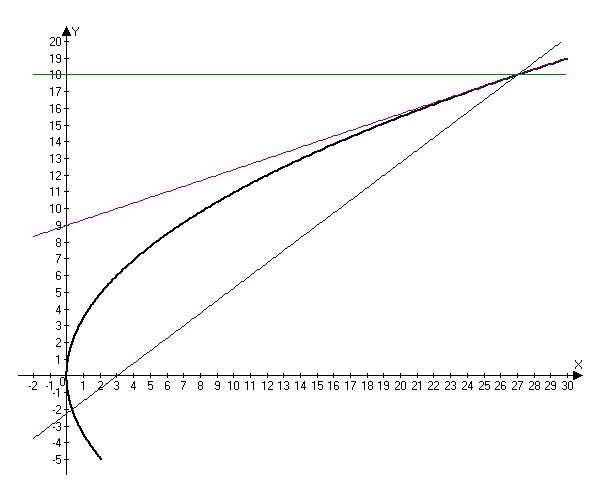
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
- Две симметричные ветви.
- Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
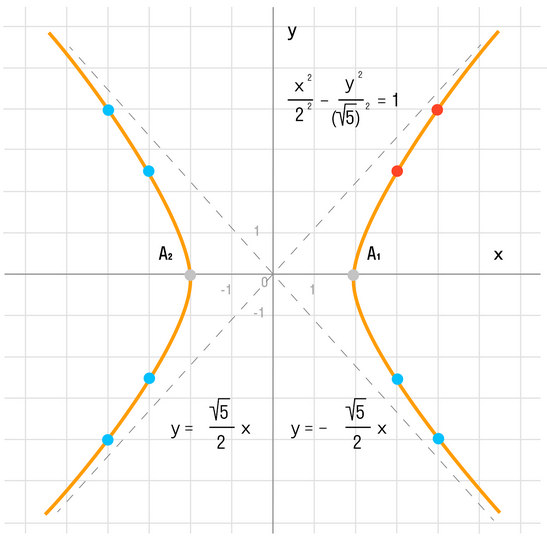
Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.
Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
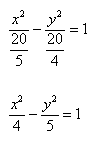
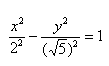
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.
Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.
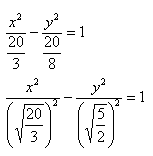
- Произведем сокращение при помощи трехэтажной дроби:
- Воспользуемся каноническим уравнением
- Найдем асимптоты гиперболы. Вот так:
Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты. - Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).
- Найдем асимптоты гиперболы. Вот так:
Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
Найдем дополнительные точки — хватит двух-трех.
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
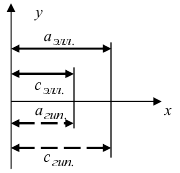
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
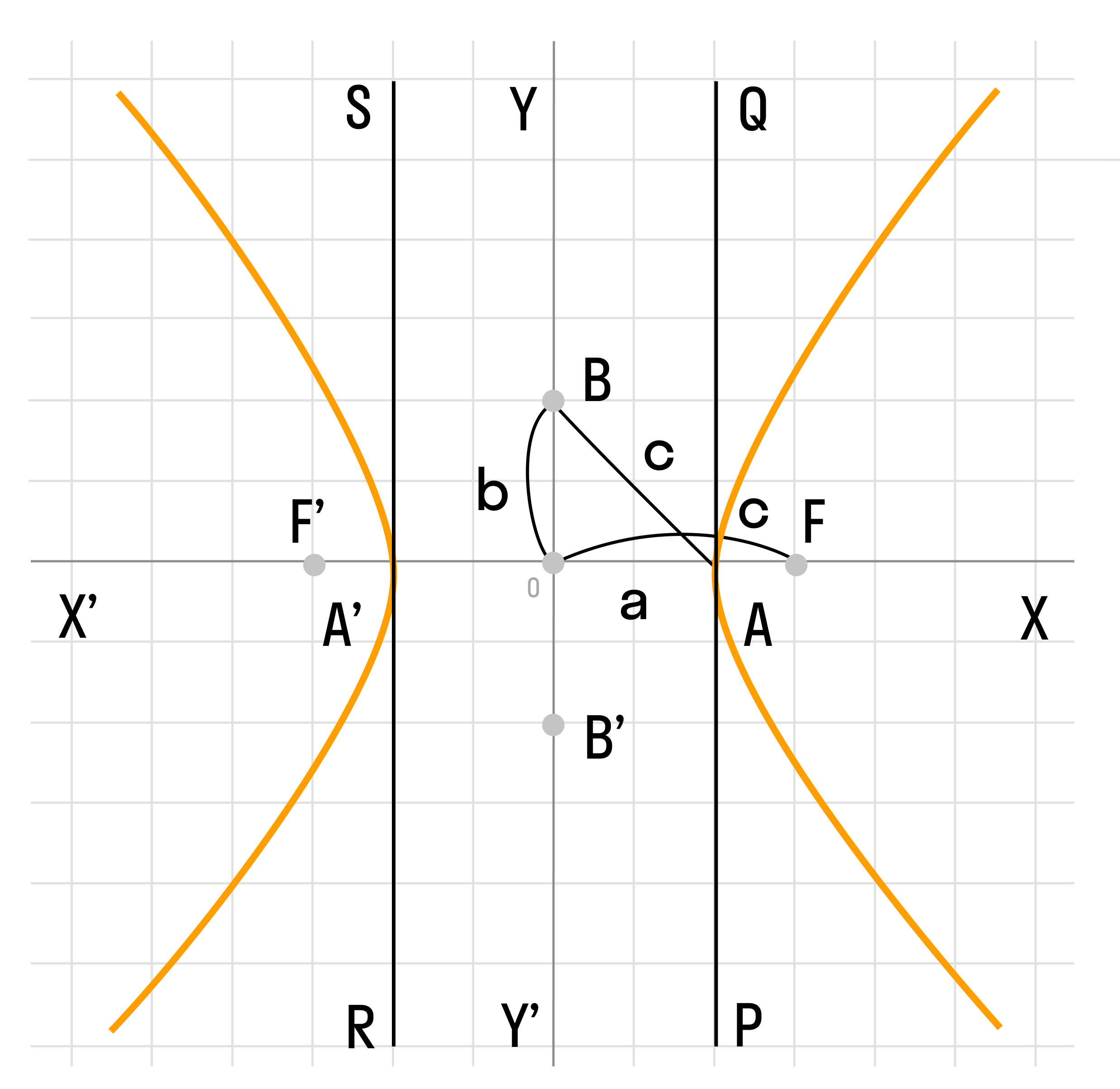
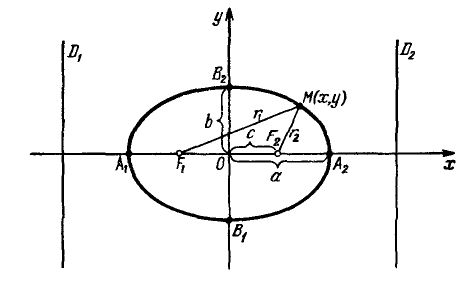
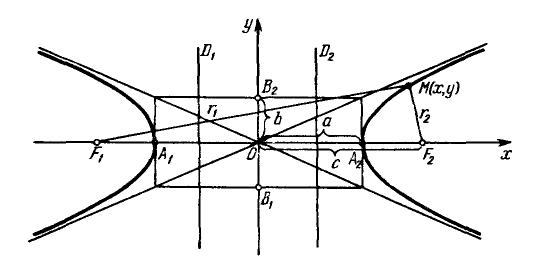
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
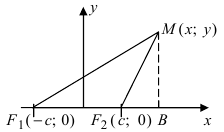
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
- пусть центр O гиперболы будет началом системы координат;
- прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
- прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.
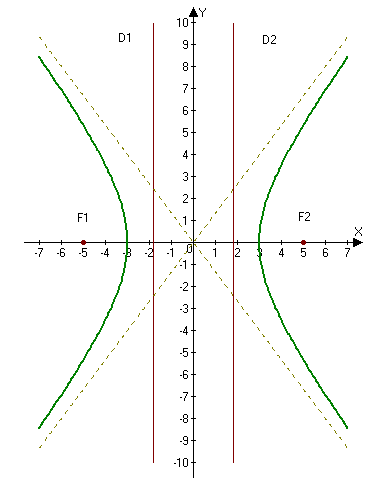
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Так как b^2 = c^2 — a^2, то величина b изменится.
При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2
Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.
Гипербола — определение и вычисление с примерами решения
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 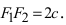
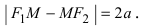
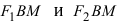
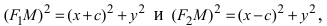
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 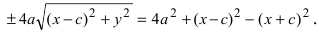
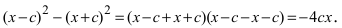
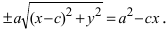
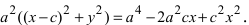
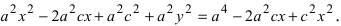
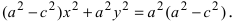
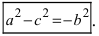
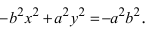
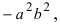
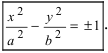
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 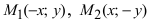
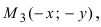
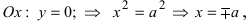
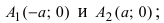
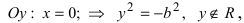
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 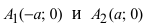
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 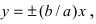
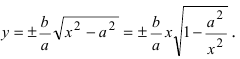
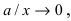
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b — мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 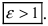
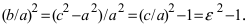
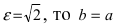
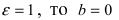
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
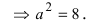
Пример:
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 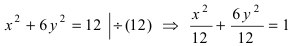
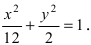
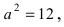
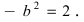
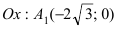
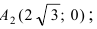
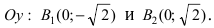
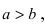
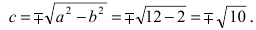
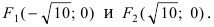
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 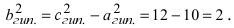
Гипербола в высшей математике
Решая его относительно 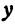
или одну двузначную функцию
Функция 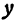

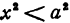
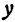
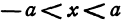
При 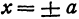
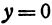
При 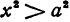
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
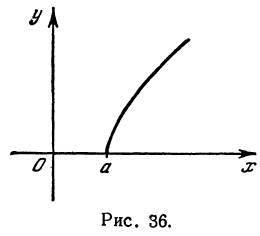
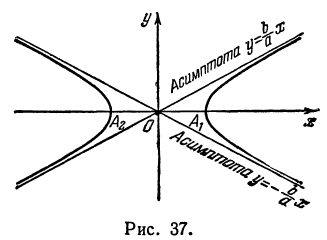
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 
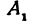
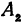
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 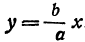
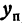
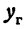
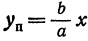
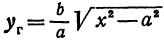
Умножим и разделим правую часть на
Будем придавать 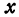
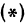

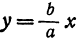
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 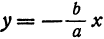
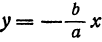
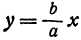
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Эллипс.
Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.
Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.
Теорема. ( Директориальное свойство эллипса)
Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$
Примеры.
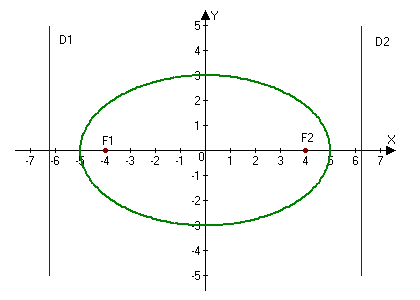
2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.
Приведем уравнение эллипса к каноническому виду:
а) Находим полуоси $a=5,$ $b=3.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<5^2-3^2>=sqrt<16>=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$
г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac<4><5>;$ г) $D_1: x=-frac<25><4>$ и $D_2: x=frac<25><4>.$
2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.
Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:
Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><2/3>=-frac<9> <2>$ и $D_2: x=frac<3><2/3>=frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$
2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.
Решение.
Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$
Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$
Таким образом, уравнение эллипса $frac<16>+frac<4>=1.$
Далее найдем координаты фокусов:
$c=sqrt=sqrt<16-4>=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$
Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$
Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$
расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.
Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.
Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.
Теорема. (Директориальное свойство гиперболы).
Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$
Примеры.
2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.
Приведем уравнение гиперболы к каноническому виду:
а) Находим полуоси $a=3,$ $b=4.$
б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$
$c=sqrt<3^2+4^2>=sqrt<25>=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$
г) Асимптоты гиперболы находим по формулам $y=pmfracx:$
д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac<5><3>;$ г) $y=pmfrac<4><3>x;$ д ) $D_1: x=-frac<9><5>$ и $D_2: x=frac<9><5>.$
2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.
Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:
Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$
Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$
$$y+3=frac<4><3>(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$
$$y+3=-frac<4><3>(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$
Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<3><5/3>=-frac<9> <5>$ и $D_2: x=frac<3><5/3>=frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$
Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$
2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.
Решение.
Проверим, что заданная точка лежит на гиперболе:
Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1.$
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:
$c=sqrtRightarrow c=sqrt<16+9>=sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$
Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$
Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$
$D_1: x=-frac<4><5/4>Rightarrow x=-frac<16><5>Rightarrow 5x+16=0;$
$D_2: x=frac<4><5/4>Rightarrow x=frac<16><5>Rightarrow 5x-16=0;$
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$
Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$
расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$
Ответ: $r_1=9/4,$ $r_2=frac<41><4>;$ $d_1=frac<41><5>;$ $d_2=frac<9><5>.$
2.273. Найти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$
Решение.
Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt<9+16>=sqrt <25>=5.$
Отсюда находим $F_1=(-5, 0).$
Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$
Чтобы н айти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений
Решим уравнение $5x^2+18x-72=0:$
Находим соответствующие координаты $y:$ $y_1=pmsqrt<24-2,4^2-10cdot 2,4>=sqrt<-5,76>$ — нет корней .
Ответ: $(-6, pm4sqrt 3).$
Парабола.
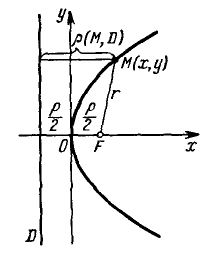
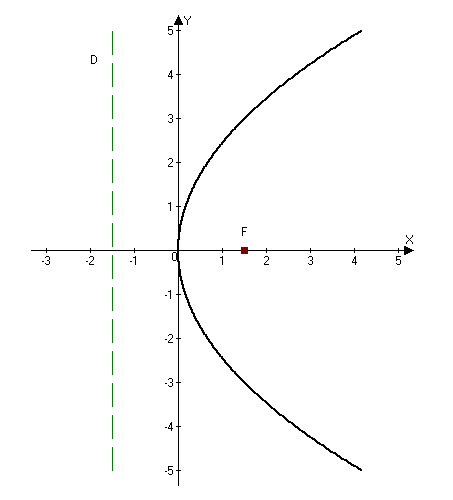
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.
Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.
Точка $Fleft(frac
<2>, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.
Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.
Примеры.
2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.
Решение.
Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $
$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$
Ответ: $p=3.$
2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$
Решение.
Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:
Ответ: $y^2=-x.$
2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$
Решение.
Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$
Приведем заданное уравнние к такому виду:
Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$
Ответ: $C(0, 2),$ $p=2.$
2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$
Решение.
Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$
Таким образом, точка $M$ имеет координаты $(3, 6).$
Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$
Далее находим фокальный параметр точки:
Ответ: $6.$
2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.
Решение.
Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$
Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$
Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac<3><4>.$
Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$
$0=frac<3><4>cdot 3+bRightarrow b=-frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=frac<3><4>x-frac<9><4>.$
Далее, найдем точку пересечения найденной прямой с параболой:
Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac<18^2><12>=frac<324><12>=27.$
Таким образом, луч пересекает параболу в точке $(27, 18).$
Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$
Подставляем все найденные значения в уравнение касательной:
$y-18=frac<1><3>(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$
Далее, найдем угол $beta$ между лучем $y=frac<3><4>x-frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac<1+k_1cdot k_2>$
$$L_2: x-3y+27=0Rightarrow y=frac<1><3>x+9Rightarrow k_2=frac<1><3>.$$
Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$
Зная $tgbeta=frac<1><3>$ и $tgalpha=k_1=frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$
$$tg(2beta-alpha)=frac<1+tg2beta tgalpha>=frac<frac<3><4>-frac<3><4>><1+frac<3><4>frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$
источники:
http://www.evkova.org/giperbola
http://mathportal.net/index.php/component/content/article/87-visshaya-matematika/analiticheskaya-geometriya/154-ellips-giperbola-parabola-direktorialnoe-svojstvo-ellipsa-i-giperboly-polyarnyj-parametr
Гипербола:
Определение: Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек
Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы
Рис. 31. Вывод уравнения гиперболы.
Расстояние между фокусами (фокусное расстояние) равно 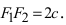
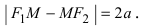
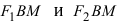
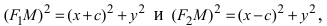
Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим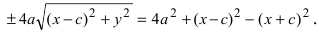
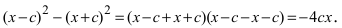
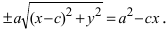
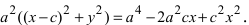
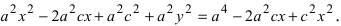
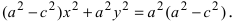
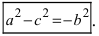
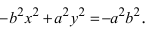
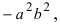
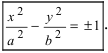
Проанализируем полученное уравнение. Если точка М(х;у) принадлежит гиперболе, то ей принадлежат и симметричные точки 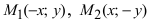
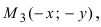
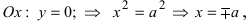
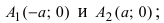
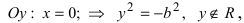
Рис. 32. Асимптоты и параметры гиперболы
Определение: Найденные точки 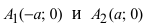
Докажем, что при возрастании (убывании) переменной х гипербола неограниченно приближается к прямым 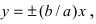
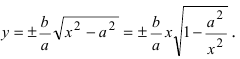
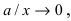
Определение: Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.
В данном конкретном случае параметр а называется действительной, а параметр b – мнимой полуосями гиперболы.
Определение: Эксцентриситетом гиперболы называется отношение фокусного расстояния к действительной полуоси гиперболы
Из определения эксцентриситета гиперболы следует, что он удовлетворяет неравенству 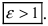
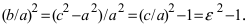
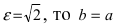
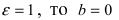
Пример:
Составить каноническое уравнение гиперболы, если мнимая полуось b = 5 и гипербола проходит через точку М(4; 5).
Решение:
Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:
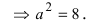
Пример:
Составить уравнение гиперболы, вершины которой находятся в фокусах, а фокусы – в вершинах эллипса
Решение:
Для определения координат фокусов и вершин эллипса преобразуем его уравнение к каноническому виду. Эллипс: 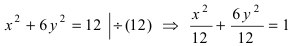
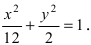
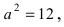
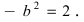
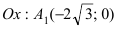
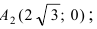
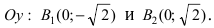
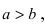
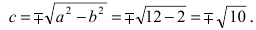
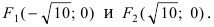
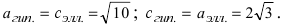
Рис. 33. Параметры эллипса и гиперболы
Вычислим длину мнимой полуоси 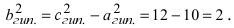
Гипербола в высшей математике
Рассмотрим уравнение
Решая его относительно 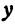
или одну двузначную функцию
Функция 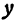

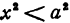
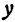
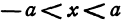
При 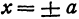
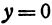
При 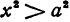
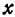
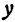
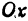
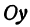
Кривая, все точки которой имеют координаты, удовлетворяющие уравнению (3), называется гиперболой.
Гипербола в силу симметрии имеет вид, указанный на рис. 37.
Точки пересечения гиперболы с осью 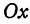
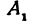
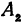
Часть гиперболы, расположенная в первой и четвертой четвертях, называется правой ветвью, а часть гиперболы, расположенная во второй и третьей четвертях, — левой ветвью.
Рассмотрим прямую, заданную уравнением 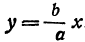
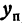
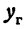
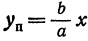
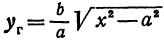
Умножим и разделим правую часть на
или
Окончательно
Будем придавать 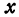
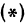

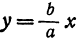
Вследствие симметрии видно, что часть правой ветви, расположенная в четвертой четверти, будет приближаться к прямой, определяемой уравнением 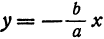
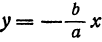
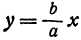
Прямая, к которой неограниченно приближается гипербола при удалении от начала координат, называется асимптотой гиперболы.
Таким образом, гипербола имеет две асимптоты, определяемые уравнениями 
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Тела вращения: цилиндр, конус, шар
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Эллипс
У этого термина существуют и другие значения, см. Гипербола.
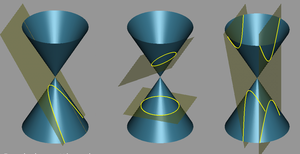
Сечения конусов плоскостью (с эксцентриситетом, большим единицы)
Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек 

причём
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, бо́льшим единицы.
История[править | править код]
Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Определения[править | править код]
Гипербола может быть определена несколькими путями.
Коническое сечение[править | править код]
Три основных конических сечения
Гипербола может быть определена как множество точек, образуемое в результате сечения кругового конуса плоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Как геометрическое место точек[править | править код]
Через фокусы[править | править код]
Гипербола может быть определена как геометрическое место точек, абсолютная величина разности расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Для сравнения: кривая постоянной суммы расстояний от любой её точки до фокусов — эллипс, постоянного отношения — окружность Аполлония, постоянного произведения — овал Кассини.
Через директрису и фокус[править | править код]
Геометрическое место точек, для которых отношение расстояния до фокуса и до заданной прямой, называемой директрисой, постоянно и больше единицы, называется гиперболой. Заданная постоянная 
Связанные определения[править | править код]
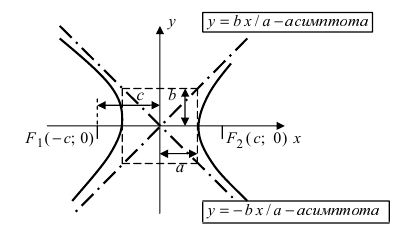
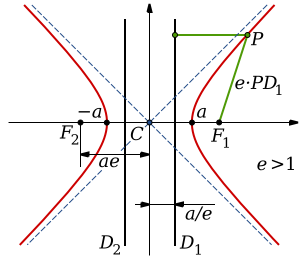
Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зелёным). Вершины гиперболы обозначены как ±a. Параметры гиперболы обозначают следующее:
a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов, F1 и F2,
θ — угол, образованный каждой из асимптот и осью, проведённой между вершинами
- Гипербола состоит из двух отдельных кривых, которые называют ветвями.
- Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами.
- Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы.
- Середина большой оси называется центром гиперболы.
- Расстояние от центра гиперболы до одной из вершин называется большой полуосью гиперболы.
- Обычно обозначается a.
- Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
- Обычно обозначается c.
- Оба фокуса гиперболы лежат на продолжении большой оси на одинаковом расстоянии от центра гиперболы. Прямая, содержащая большую ось гиперболы, называется действительной, или поперечной, осью гиперболы.
- Прямая, перпендикулярная действительной оси и проходящая через её центр, называется мнимой, или сопряжённой, осью гиперболы.
- Отрезок между фокусом гиперболы и гиперболой, перпендикулярный её действительной оси, называется фокальным параметром.
- Расстояние от фокуса до асимптоты гиперболы называется прицельным параметром.
- Обычно обозначается b.
- В задачах, связанных с движением тел по гиперболическим траекториям, расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
- Обычно обозначается
.
- Обычно обозначается
Соотношения[править | править код]
Для характеристик гиперболы, определённых выше, существуют следующие соотношения
.
.
.
.
.
.
.
.
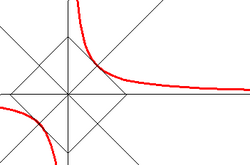
Равнобочная гипербола[править | править код]
Гиперболу, у которой 
Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
при этом фокусы гиперболы располагаются в точках (a, a) и (−a, −a).
Равнобочная гипербола является графиком обратной пропорциональности, задаваемой формулой
Эксцентриситет такой гиперболы равен 
Гипербола Киперта[править | править код]
Точка на гиперболе Киперта
Равнобочная гипербола как гипербола Киперта может быть определена через треугольники в трилинейных координатах[1] в виде геометрического места точек 
- Если три треугольника
,
и
построены на сторонах треугольника
, являются подобными, равнобедренными с основаниями на сторонах исходного треугольника, и одинаково расположенными (то есть все они построены либо с внешней стороны, либо с внутренней стороны), то прямые
,
и
пересекаются в одной точке
.
Если общий угол при основании равен 
Уравнения[править | править код]
Декартовы координаты[править | править код]
Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
,
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
и
Канонический вид[править | править код]
Перемещением центра гиперболы в начало координат и вращением её относительно центра уравнение гиперболы можно привести к каноническому виду:
,
где 

Полярные координаты[править | править код]
Гипербола в полярных координатах
Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
Уравнения в параметрической форме[править | править код]
Подобно тому, как эллипс может быть представлен уравнениями в параметрической форме, в которые входят тригонометрические функции, гипербола в прямоугольной системе координат, центр которой совпадает с её центром, а ось абсцисс проходит через фокусы, может быть представлена уравнениями в параметрической форме, в которые входят гиперболические функции[3].

В первом уравнении знак «+» соответствует правой ветви гиперболы, а «−» — её левой ветви.
Свойства[править | править код]
- Оптическое свойство. Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
- Для любой точки, лежащей на гиперболе, отношение расстояний от этой точки до фокуса к расстоянию от этой же точки до директрисы есть величина постоянная.
- Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
- Каждая гипербола имеет сопряжённую гиперболу, для которой действительная и мнимая оси меняются местами, но асимптоты остаются прежними. Сопряжённая гипербола не является результатом поворота начальной гиперболы на угол 90°; гиперболы различаются формой при
.
- Отрезок касательной в каждой точке гиперболы, заключенный между двумя асимптотами гиперболы, делится точкой касания пополам и отсекает от двух асимптот треугольник постоянной площади.
Асимптоты[править | править код]
Две сопряжённые гиперболы (голубая и зелёная) обладают совпадающими асимптотами (красные). Эти гиперболы единичные и равнобочные, так как a = b = 1
Уравнения асимптот для гиперболы, заданной в каноническом виде
выводятся следующим образом. Пусть 

Таким образом, уравнения двух асимптот имеют вид:

или
Диаметры и хорды[править | править код]
Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент 

Если диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными. Главными диаметрами называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Определение центра гиперболы
Касательная и нормаль[править | править код]
Поскольку гипербола является гладкой кривой, в каждой её точке (x0, y0) можно провести касательную и нормаль. Уравнение касательной к гиперболе, заданной каноническим уравнением, имеет вид:
,
или, что то же самое,
.
| Вывод уравнения касательной |
|---|
|
Уравнение касательной произвольной плоской линии имеет вид Каноническое уравнение гиперболы можно представить в виде пары функций
Тогда производная этих функций имеет вид
Подставив это уравнение в общее уравнение касательной, получим |
Уравнение нормали к гиперболе имеет вид:
.
| Вывод уравнения нормали |
|---|
|
Уравнение нормали произвольной плоской линии имеет вид
Каноническое уравнение гиперболы можно представить в виде пары функций
Тогда производная этих функций имеет вид
Подставив это уравнение в общее уравнение нормали, получим
|
Кривизна и эволюта[править | править код]
Синим цветом показана гипербола. Зелёным цветом — эволюта правой ветви этой гиперболы (эволюта левой ветви вне рисунка. Красным цветом показан круг, соответствующий кривизне гиперболы в её вершине)
Кривизна гиперболы в каждой её точке (x, y) определяется из выражения:
.
Соответственно, радиус кривизны имеет вид:
.
В частности, в точке (a, 0) радиус кривизны равен
.
| Вывод формулы для радиуса кривизны |
|---|
|
Формула для радиуса кривизны плоской линии, заданной параметически, имеет вид:
Воспользуемся параметрическим представлением гиперболы: Тогда, первая производная x и y по t имеет вид
а вторая производная – Подставляя эти значения в формулу для кривизны получаем:
|
Координаты центров кривизны задаются парой уравнений:
Подставив в последнюю систему уравнений вместо x и y их значения из параметрического представления гиперболы, получим пару уравнений, задающих новую кривую, состоящую из центров кривизны гиперболы. Эта кривая называется эволютой гиперболы.
Эллиптическая система координат
Обобщение[править | править код]
Гипербола есть синусоидальная спираль при 
Применение[править | править код]
- Семейство конфокальных (софокусных) гипербол вместе с семейством софокусных эллипсов образуют двумерную эллиптическую систему координат.
- Другие ортогональные двумерные координатные системы, построенные с помощью гипербол, могут быть получены с помощью других конформных преобразований. Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
- Инверсией гиперболы с центром, лежащим в её собственном центре, в фокусе или на вершине можно получить соответственно лемнискату Бернулли, улитку Паскаля или строфоиду.
- Гиперболы можно видеть на многих солнечных часах. В течение любого дня года Солнце описывает окружность на небесной сфере, и его лучи, падающие на верхушку гномона солнечных часов, описывают конус света. Линия пересечения этого конуса с плоскостью горизонтальных или вертикальных солнечных часов является коническим сечением. На наиболее населённых широтах и в большую часть года это коническое сечение является гиперболой. На солнечных часах часто показаны линии, описываемые тенью от верхушки гномона в течение дня для нескольких дней года (например, дней летнего и зимнего солнцестояний), таким образом, на них часто можно видеть определённые гиперболы, вид которых различен для различных дней года и различных широт.
Гиперболы, соответствующие на плоскости траекториям первых межзвёздных объектов — 1I/Оумуамуа (зелёная линия) и 2I/Borisov (синия линия)
- АМС, преодолевая притяжение основного влияющего на неё тела и далеко улетая от него, при отсутствии возмущений, должна двигаться по гиперболической траектории или параболической траектории, поскольку в таком случае теоретически возможно удаление до бесконечности от данного тела[4]. В частности, гиперболическими относительно Солнца являются траектории АМС «Вояджер-1» и АМС «Вояджер-2», с эксцентриситетом 3,7 и 6,3 и большой полуосью 480,9 млн км и 601,1 млн км соответственно[5][6]. Гиперболическая траектория небесного тела в Солнечной системе может указывать на его межзвёздное происхождение. В конце 2010-х годов были открыты первый межзвёздный астероид и первая межзвёздная комета[7], их траектории — гиперболические. Однако известные ранее кометы с гиперболической траекторией небольшого эксцентриситета только собираются стать межзвёздными: испытав во время своей «жизни» в Солнечной системе возмущение от такой планеты, как Юпитер, они ложатся на межзвёздный курс[8].
См. также[править | править код]
- Гиперболоид
- Гиперболы, описанные около треугольника
- Каустика
- Конические сечения
- Кривая второго порядка
- Окружность
- Парабола
- Эллипс
- Кривая постоянной суммы расстояний между двумя точками — эллипс,
- Кривая постоянной разности расстояний между двумя точками — гипербола,
- Кривая постоянного отношения — окружность Аполлония,
- Кривая постоянного произведения — овал Кассини.
- Сглаженный восьмиугольник § Построение
Примечания[править | править код]
- ↑ Eddy, R. H. and Fritsch, R. The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle. Math. Mag. 67, pp. 188—205, 1994.
- ↑ Шнейдер В.Е. Краткий курс высшей математики. — Рипол Классик. — ISBN 9785458255349.
- ↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 15—16. — 288 с.
- ↑ Сихарулидзе Ю. Г. Баллистика летательных аппаратов. — М.: Наука, 1982. — С. 162—163. — 5750 экз.
- ↑ Voyager – Hyperbolic Orbital Elements. НАСА. Дата обращения: 29 октября 2019. Архивировано 6 мая 2021 года.
- ↑ Ulivi P., Harland D. M. Robotic Exploration of the Solar System. Part I: The Golden Age 1957-1982. — Springer, Praxis, 2007. — P. 441. — ISBN 978-0-387-49326-8. Содержит эксцентриситет орбиты АМС «Вояджер-2» относительно Солнца после пролёта Нептуна.
- ↑ Naming of New Interstellar Visitor: 2I/Borisov. МАС (24 сентября 2019). Дата обращения: 24 сентября 2019. Архивировано 23 апреля 2020 года.
- ↑ Carl Sagan, Ann Druyan. Comet. — New York: Ballantine Books, 1997. — P. 104. — ISBN 0-345-41222-2.
Литература[править | править код]
- Бронштейн И. Гипербола // Квант. — 1975. — № 3.
- Граве Д. А. Гиперболы // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982.
- Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — Вып. 4. Архивировано 14 сентября 2008 года.
Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Гиперболой
называется геометрическое место точек,
для которых разность
расстояний от двух фиксированных точек
(называемых фокусами) есть величина
постоянная. Причем указанная разность
берется по абсолютному значению и
необходимо, что бы она была меньше
расстояния между фокусами и не равна
нулю. (См. Рис.23)

Рис.23
На
рисунке:
–
– левый фокальный радиус;
–
–
правый фокальный радиус;
–
(- с; 0) – координаты левого фокуса (точки
F1);
–
(с; 0) – координаты правого фокуса (точки
F2);
–
– действительная
полуось
гиперболы;
–
– мнимая
полуось гиперболы;
–
точка (а; 0) – правая вершина гиперболы;
–
точка (- а; 0) – левая вершина гиперболы;
–
прямые
– асимптоты гиперболы.
Названия
полуосей не случайны: точки
гиперболе принадлежат, а точки
–
гиперболе не принадлежат (потому и ось
– мнимая), но мнимая полуось, хотя и не
является частью гиперболы, вполне
определяет ее форму, поскольку именно
между асимптотами гиперболы и располагаются
ветви ее.
Каноническое уравнение гиперболы
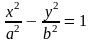
(смотри
замечание о каноничности уравнения).
Связь между полуосями и координатами фокусов гиперболы
При
этом важным является выражение,
связывающее действительную, мнимую
полуось и координату фокуса (сравните
с формой аналогичной связи для параметров
эллипса)
.
Эксцентриситет
гиперболы

Пример 19 (о нахождении уравнения гиперболы)
Эксцентриситет
гиперболы равен
.
Найти каноническое уравнение гиперболы,
если точка
гиперболе принадлежит.
Решение
Прежде
всего, что ищем конкретно? – Ищем значения
a
и b
в каноническом уравнении гиперболы.
Неизвестных величин две, следовательно,
и уравнений для их нахождения должно
быть два.
Первое
уравнение получим из того факта, что
нам известен эксцентриситет гиперболы
и известна связь
между полуосями и координатами фокуса
гиперболы:
.
Это
первое равенство, а второе получим,
используя тот факт, что точка М гиперболе
принадлежит, т.е., ее координаты обращают
каноническое уравнение гиперболы в
тождество:
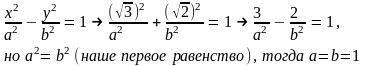
и,
окончательно, получаем
Ответ
Искомая
гипербола описывается каноническим
уравнением
x2
– y2
= 1.
Пример 20 (прямая и гипербола)
Через
точку М(0; – 1) и правую вершину гиперболы
3∙x2
– 4∙y2
= 12
проведена
прямая. Найти вторую точку пересечения
прямой с гиперболой.
Решение
Задачу
будем решать в два шага:
–
найдем уравнение прямой;
–
найдем координату точки пересечения
прямой и гиперболы.
Шаг
1
Для
нахождения уравнения прямой, проходящей
через точку М(0; – 1) и правую вершину
гиперболы необходимо знать координаты
правой вершины гиперболы. Найдем вторую
точку из уравнения гиперболы, приведя
данное уравнение к каноническому
виду,
зная при этом, что в каноническом
уравнении важно все: равно выражение
именно
единице, а в самом выражении – значения
действительной и мнимой полуоси – это
знаменатели дробей, в которых числители
x2
и y2.

Откуда
в уравнении гиперболы a
= 2, b
=
,
или координаты правой вершины М2(2;
0). А вот теперь ищем уравнение
прямой, проходящей через две данные
точки
М и М2

Шаг
2
Ищем
координаты точек пересечения найденной
прямой и данной гиперболы. Эти координаты
удовлетворяют обоим уравнениям, т.е.
являются решением системы уравнений
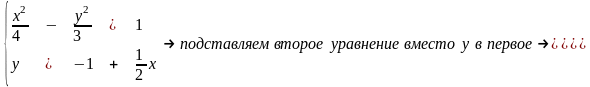
Решаем
полученное уравнение и находим, что x1
= – 4, x2
= 2.
Подставляем
найденные x1
и x2
во второе уравнение системы и находим
координаты точек пересечения прямой с
гиперболой N1(-
4; -3) и N2(2;
0).
Не
трудно убедиться (проверьте самостоятельно)
что точка М гиперболе не принадлежит,
а значит, точек пересечения будет две.
Ответ
Точки
пересечения прямой и гиперболы – N1(-
4; -3) и N2(2;
0).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #