Пример 1:
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
1) координаты и модули векторов А1 А2и А1 А4;
2) угол между ребрами А1 А2и А1 А4;
3) площадь грани А1 А2 А3;
4) объем пирамиды;
5) уравнение прямой А1 А2;
6) уравнение плоскости А1 А2 А3;
7) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
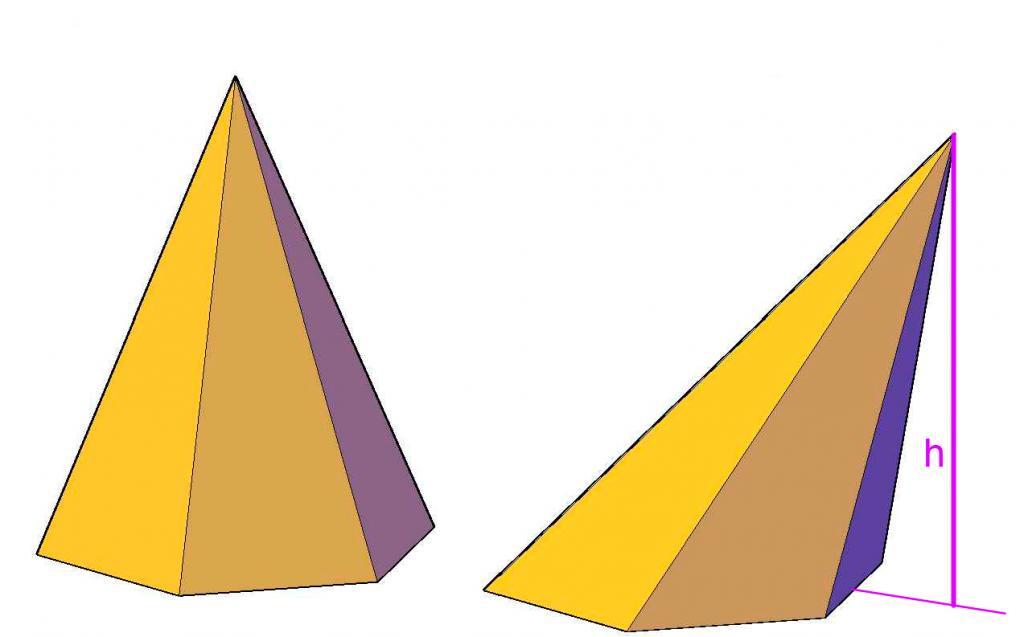
Сделать чертеж.
А1 (0; 4; -4), А2 (5; 1; -1), А3 (-1; -1; 3), А4 (0; -3; 7).
Решение от преподавателя:



Пример 2:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
1. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
Решение от преподавателя:






Пример 3:

Решение от преподавателя:
Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-3)(1*2-0*3) – (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y – 3z-38 = 0
Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
Уравнение прямой A1A4: ![]()
γ = arcsin(0.267) = 15.486o
Уравнение высоты пирамиды через вершину A4(0,2,2)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0 ![]()
![]()
Уравнение плоскости через вершину A4(0,2,2)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
2(x-0)+13(y-2)-3(z-2) = 0
или
2x+13y-3z-20 = 0
Пример 4:

Решение от преподавателя:
Даны координаты пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
- Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-0)(3*2-8*3) – (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x – 15y + 33z-18 = 0
Упростим выражение: -6x – 5y + 11z-6 = 0
2) Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
Уравнение прямой A1A4: 


γ = arcsin(0.193) = 11.128o
3) Уравнение высоты пирамиды через вершину A4(0,5,4)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0


4) Уравнение плоскости через вершину A4(0,5,4)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости
Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
-6(x-0)-5(y-5)+11(z-4) = 0
или
-6x-5y+11z-19 = 0
5) Координаты вектора A1A4(0;4;3)
Уравнение прямой, проходящей через точку А1(0,1,1) параллельно вектору А1А2(0,4,3) имеет вид:

Пример 5:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:




Пример 6:

Решение от преподавателя:
1) Даны координаты вершин пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
Координаты векторов.
Координаты векторов: A1A2(3;3;3) A1A4(0;4;3)
Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 


Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:  , где a1a2 = X1X2 + Y1Y2 + Z1Z2
, где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(3;3;3) и A1A3(0;4;3):

А1 = arccos(0,808)
Найдем площадь грани с учётом геометрического смысла векторного произведения:
S =![]()
Найдем векторное произведение
=i(3*2-8*3) – j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i – 15j + 33k

3) Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
Координатывекторов:A1A2(3;3;3) A1A3(-3;8;2) A1A4(0;4;3) :
|
|
|
где определитель матрицы равен:
∆ = 3*(8*3-4*2)-(-3)*(3*3-4*3)+0*(3*2-8*3) = 39
Пример 7:

Решение от преподавателя:
- Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):
γ = arccos(0) = 90.0030 - Площадь грани
Площадь грани можно найти по формуле:
где
Найдем площадь грани A1A2A3
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):

Площадь грани A1A2A3 - Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
|
|
|
где определитель матрицы равен:
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18
Пример 8:
Даны координаты вершин пирамиды А1А2А3А4 . Найти:
1) длину ребра А1А2;
2) угол между рёбрами А1А2 и А1А4 ;
3) угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объём пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
Сделать чертёж.
А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8).
Решение от преподавателя:
1) Длина ребра A1A2;

2) угол между ребрами А1А2 и А1А4;

3) угол между ребрами А1А4 и гранью А1А2А3;

Найдем уравнение стороны А1А4:

Вектор нормали: ![]() к плоскости А1А2А3.
к плоскости А1А2А3. ![]()

4) площадь грани А1А2А3;
![]()
5) объем пирамиды;

6) уравнение прямой А1А2;

7) уравнение плоскости А1А2А3;

Итак: z=4 – уравнение плоскости А1А2А3.
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
A4O – высота:
Уравнение A4O:
![]()
Т.к. ![]() , то
, то
![]()
В результате получаем уравнение высоты:
![]()


Пример 9:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:


Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Длина ребра пирамиды через вектора
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет – тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку “Зарегистрироваться” вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу – ответит приведенная ниже статья.
Что представляет собой пирамида?
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
 Вам будет интересно: Какую роль играет репродуктивная клетка животных и растений?
Вам будет интересно: Какую роль играет репродуктивная клетка животных и растений?
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания – это высота фигуры.
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
Как рассчитывается объем пирамиды?
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
Здесь So – это основания площадь, h – расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) – координаты точки.
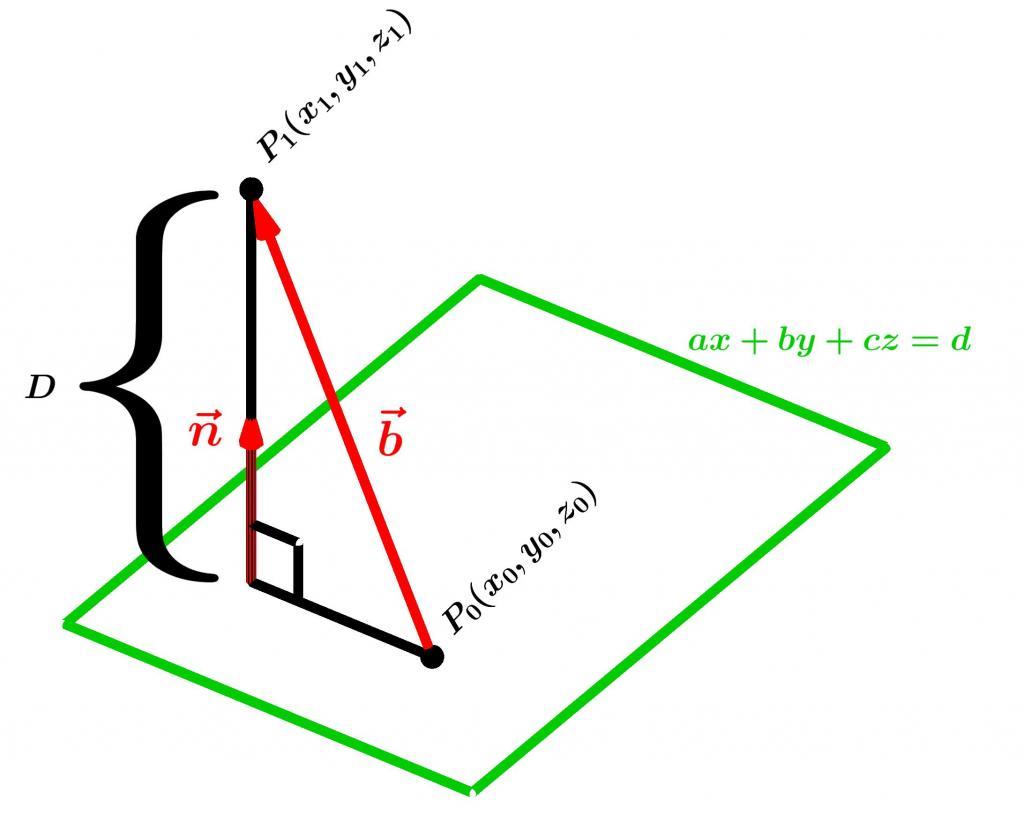
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды – треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x – 10 * y – 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 – 10 * 3 – 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.
[spoiler title=”источники:”]
http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-koordinaty-vershin-piramidy
http://1ku.ru/obrazovanie/51574-kak-rasschitat-obem-piramidy-po-koordinatam-vershin-metodika-i-primer-zadachi/
[/spoiler]
Векторная алгебра и элементы аналитической геометрии
ЗАДАЧА 1
В декартовой прямоугольной системе координат даны вершины пирамиды А1 В1 С1 D1. Найдите:
А) длину ребра А1 В1;
Б) косинус угла между векторами ![]() ;
;
В) уравнение ребра А1 В1;
Г) уравнение грани А1 В1 С1;
Д) уравнение высоты, опущенной из вершины D1 на грань А1 В1 С1;
Е) координаты векторов ![]() ,
, ![]() ,
, ![]() , и докажите, что они образуют линейно независимую систему;
, и докажите, что они образуют линейно независимую систему;
Ж) координаты вектора ![]() , где
, где ![]() – середины ребер А1 D1 и В1 С1 соответственно;
– середины ребер А1 D1 и В1 С1 соответственно;
З) разложение вектора ![]() по базису
по базису ![]() если А1(–2,2,2), В1(1,–3,0), С1(6,2,4), D1(5,7,–1).
если А1(–2,2,2), В1(1,–3,0), С1(6,2,4), D1(5,7,–1).
Решение
А) Найдем координаты вектора ![]() по формуле
по формуле
![]() =
= ![]() XВ
XВ ![]() – XА
– XА ![]() ; YВ
; YВ ![]() – YА
– YА ![]() ; ZВ
; ZВ ![]() – ZА
– ZА ![]()
![]() , где (ХА
, где (ХА ![]() , YА
, YА ![]() , ZА
, ZА ![]() ) – координаты точки А1, (ХВ
) – координаты точки А1, (ХВ ![]() , YВ
, YВ ![]() , ZВ
, ZВ ![]() ) – координаты точки В1.
) – координаты точки В1.
Итак, ![]() =
= ![]() Тогда
Тогда ![]() =
= ![]() .
.
Итак, длина отрезка ![]() (или длина вектора
(или длина вектора ![]() ) равна
) равна ![]() . Это и есть искомая длина ребра.
. Это и есть искомая длина ребра.
Б) Координаты вектора ![]() =
= ![]() уже известны, осталось определить координаты вектора
уже известны, осталось определить координаты вектора ![]() :
: ![]() =
= ![]() .
.
Угол между векторами ![]() и
и ![]() вычислим по формуле Cos
вычислим по формуле Cos ![]() =
= 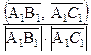 ,
,
Где скалярое произведение векторов ![]() и
и ![]() равно (
равно ( ![]() ,
, ![]() )= 3 ´ 8 + (–5) ´ 0 + (–2) ´2 = 24 + 0 – 4=20,
)= 3 ´ 8 + (–5) ´ 0 + (–2) ´2 = 24 + 0 – 4=20, ![]() =
= ![]() ,
, ![]() =
= ![]()
Итак, Cos ![]() =
= ![]() =
= ![]() .
.
В) Координаты точки А1(–2,2,2) обозначим соответственно Х0 = –2, У0 = 2, Z0=2, а координаты точки В1 (1,–3,0) через Х1=1, У1 = –3, Z1=0 и воспользуемся уравнением прямой в пространстве, проходящей через две точки: ![]() .
.
Следовательно, уравнение ребра А1В1 имеет вид ![]() или
или ![]()
Г) Обозначим координаты векторов ![]() и
и ![]() через Х1=3, У1= –5,
через Х1=3, У1= –5, ![]() 1= –2 и Х2=8, У2= 0,
1= –2 и Х2=8, У2= 0, ![]() 2=2 соответственно. Векторное произведение данных векторов определяется формулой
2=2 соответственно. Векторное произведение данных векторов определяется формулой
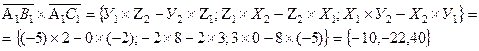
Так как данный вектор перпендикулярен грани А1 В1 С1 то можно воспользоваться уравнением плоскости, проходящей через точку (Х0, У0, ![]() 0) перпендикулярно вектору
0) перпендикулярно вектору ![]() , которое имеет вид
, которое имеет вид
А ![]() .
.
Подставим координаты точки А1 (Х0=–2, У0=2, ![]() 0=2) и координаты перпендикулярного вектора А=–10, В=–22, С=40 в это уравнение:
0=2) и координаты перпендикулярного вектора А=–10, В=–22, С=40 в это уравнение:
– 10 ( Х + 2 ) – 22 (У – 2) + 40 ( ![]() – 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (– 20 + 44–80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: –10х – 22у + 40 z–56=0 или
– 2) = 0. Раскроем скобки и приведем подобные члены – 10 х – 22 у + 40z + (– 20 + 44–80)=0. Итак, уравнение грани А1 В1 С1 имеет вид: –10х – 22у + 40 z–56=0 или
–5х – 11у + 20 z – 28=0.
Д) Вектор ![]() является направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку
является направляющим вектором высоты, опущенной из вершины D1 на грань А1В1С1. Воспользуемся уравнением прямой в пространстве, проходящей через точку ![]() с заданным направляющим вектором:
с заданным направляющим вектором: ![]() , где
, где ![]() – координаты точки D1. Отсюда искомое уравнение:
– координаты точки D1. Отсюда искомое уравнение: ![]() или
или ![]()
Е) Координаты вектора ![]() =
= ![]() =
= ![]() .
.
Обозначим ![]()
![]() =
= ![]() ,
, ![]()
![]() =
= ![]() ,
, ![]() .
.
Чтобы доказать, что векторы ![]() образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
образуют линейно независимую систему векторов необходимо убедиться, что определитель третьего порядка, составленный из координат этих векторов,
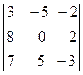 отличен от 0. Определитель третьего порядка равен
отличен от 0. Определитель третьего порядка равен
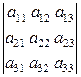 =
= 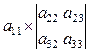 –
– 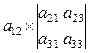 +
+ 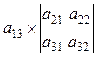 =
=
= ![]()
Вычислим определитель
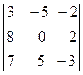 =3
=3 ![]() – (–5)
– (–5) ![]() +(–2)
+(–2) ![]() = 3
= 3 ![]() (0
(0 ![]() (–3) – 5
(–3) – 5 ![]() 2)+5
2)+5 ![]() (8
(8 ![]() (–3) – 7
(–3) – 7 ![]() 2) –
2) –
– 2 ![]() (8
(8 ![]() 5 – 7
5 – 7 ![]() 0) =3
0) =3 ![]() (–10)+5
(–10)+5 ![]() (–24 – 14) – 2
(–24 – 14) – 2 ![]() 40=–30 – 190 – 80 = –300.
40=–30 – 190 – 80 = –300.
Так как данный определитель отличен от 0, то вектора ![]() образуют линейно независимую систему.
образуют линейно независимую систему.
Ж) Сначала найдем координаты точек М и N соответственно. Координаты точки
М = 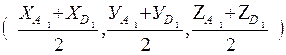 =
= ![]() =
= 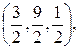
N = 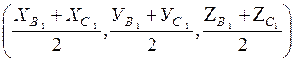 =
= 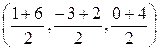 =
= 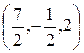 .
.
Получаем вектор ![]() =
= ![]() .
.
З) Обозначим через ![]() координаты вектора
координаты вектора ![]() в базе
в базе ![]() .
.
Тогда ![]() =
= ![]() =
= ![]() .
.
Так как
![]() =
= ![]() +
+ ![]() +
+ ![]() ;
; ![]()
= ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
То приравнивая соответствующие координаты, получим систему трех линейных уравнений с тремя неизвестными.
(1) 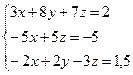
Решим данную систему уравнений с помощью формул Крамера (см. ![]() глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
глава 10, стр. 268). Рассмотрим произвольную систему трех линейных уравнений с тремя неизвестными:
(2) 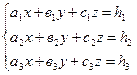
Тогда ![]() =
= ![]() z
z ![]() , где
, где
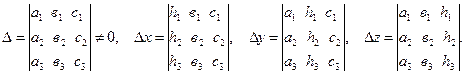
Для системы (1) определитель
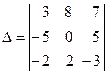 =3
=3 ![]() –8
–8 ![]() +7
+7 ![]() =
=
= 3 ( –10) – 8 ![]() ( 15 + 10 ) + 7 ( –10) = –30 – 200 – 70 = –300;
( 15 + 10 ) + 7 ( –10) = –30 – 200 – 70 = –300;
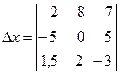 = 2
= 2 ![]() –8
–8 ![]() +7
+7 ![]() =
=
![]()
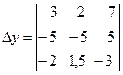 =3
=3 ![]() –2
–2 ![]() +7
+7 ![]() =
=
=3 ![]()
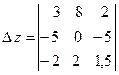 =3
=3 ![]() –8
–8 ![]() +2
+2 ![]() =
=
= ![]()
По формулам Крамера ![]()
![]()
Итак, разложение вектора ![]() по базису (
по базису ( ![]() ) имеет вид
) имеет вид
![]() =
= ![]()
ЗАДАЧА 2
Решите систему линейных уравнений
А) методом Крамера;
Б) методом Гаусса;
В) с помощью обратной матрицы.
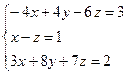
Решение
А) Метод Крамера состоит в решении системы линейных уравнений по формулам Крамера ![]() ,
,
Где ![]() (Подробности смотрите в пункте З) задачи 1.
(Подробности смотрите в пункте З) задачи 1.
Так как ![]()
![]()
![]()
![]() ; то
; то ![]()
Б) решим данную систему уравнений методом Гаусса. Метод Гаусса состоит в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида из которой последовательно, начиная с последнего уравнения легко находят все неизвестные системы.
Составим расширенную матрицу данной системы.
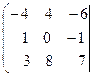
![]()
Поменяем местами первую и вторую строки матрицы чтобы в ее левом верхнем углу была единица. Получим матрицу,
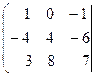
![]()
Умножим каждый элемент первой строки матрицы на 4 и прибавим полученные числа к соответствующим элементам второй строки. Матрица примет вид,
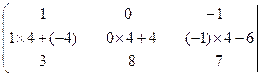
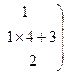 =
= 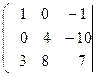
![]()
Умножим каждый элемент первой строки матрицы на –3, и прибавим полученные числа к соответствующим элементам третьей строки. Получим:
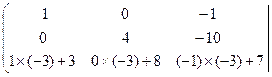
 =
= 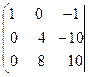
![]() .
.
Разделим каждый элемент второй строки матрицы на 4, чтобы второй элемент, стоящий на главной диагонали матрицы, стал равным 1.
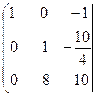
![]() .
.
Умножим каждый элемент второй строки матрицы на –8 и прибавим полученные числа к соответствующим элементам третьей строки:
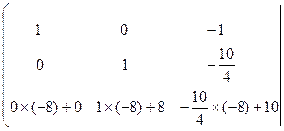
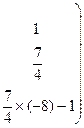

![]() .
.
Данная матрица соответствует системе уравнений 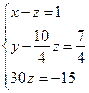 , решение которой совпадает с решением исходной системы. Начиная с последнего уравнения, несложно найти все неизвестные.
, решение которой совпадает с решением исходной системы. Начиная с последнего уравнения, несложно найти все неизвестные.
Действительно, так как ![]() и
и ![]() , то
, то ![]()
Отсюда, ![]() Из
Из ![]() имеем
имеем ![]()
Ответ: ![]() .
.
В) Решение системы в этом случае равно ![]() =
= ![]()
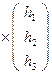 , где
, где ![]() =
= 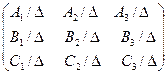 – обратная матрица для матрицы
– обратная матрица для матрицы ![]() =
= 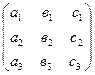 ,
, ![]() – столбец свободных членов,
– столбец свободных членов, ![]() – определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
– определитель этой матрицы. (Общую запись системы трех линейных уравнений с тремя неизвестными смотрите в задаче 1, пункт з, система 2).
Составим матрицу состоящую из коэффициентов при неизвестных данной системы:
А = 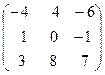 .
.
Вычислим ее определитель 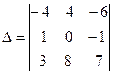 = –4
= –4 ![]() –4
–4 ![]() –6
–6 ![]() =
=
= ![]() .
.
Вычислим алгебраические дополнения для всех элементов матрицы А:
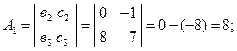
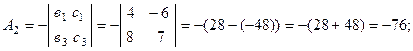
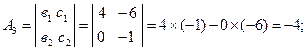
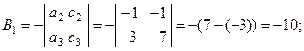
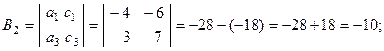
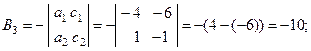
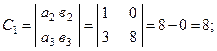
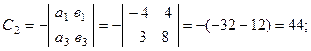
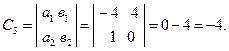
Тогда ![]()
![]() =
= 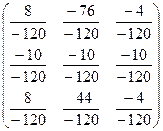 =
= 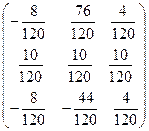 и
и
![]() =
= 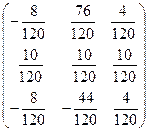
![]()
![]() =
=
= 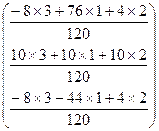 =
= 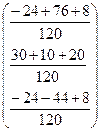 =
= 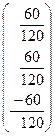 =
= ![]() .
.
Отметим, что ответы, полученные при решениями разными методами совпадают между собой.
Ответ: ![]()
| < Предыдущая | Следующая > |
|---|



