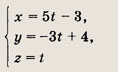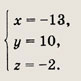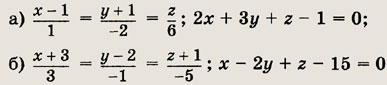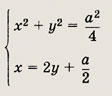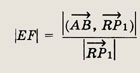Как найти длины сторон параллелограмма по векторам

Площадь параллелограмма построенного на векторах

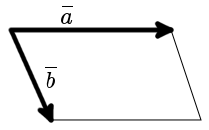
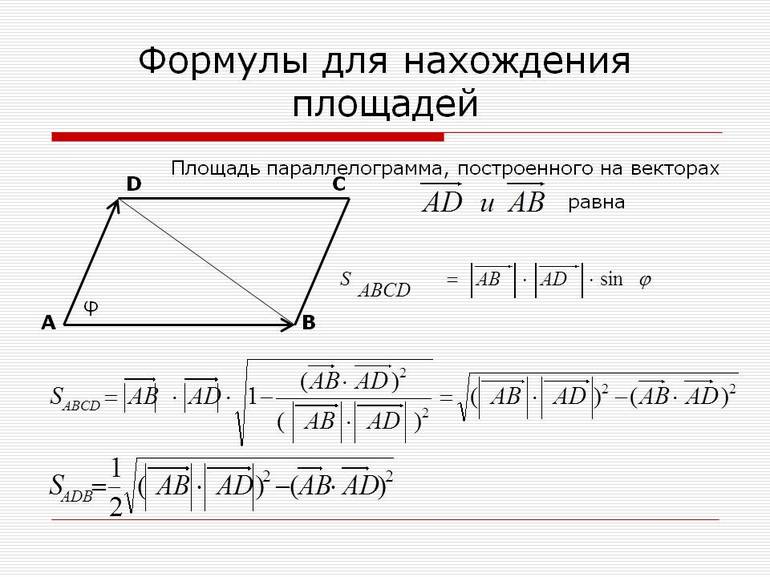
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье площадь параллелограмма. Площадь будет равняться произведению модулей на синус угла между ними:

Рассмотрим пример расчета площади параллелограмма построенного на векторах.

Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами

Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a (x1;y1;z1), а вектора b (x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:


Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.

Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.

Онлайн калькулятор. Площадь параллелограмма построенного на векторах.

Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.

Калькулятор для вычисления площади параллелограмма построенного на векторах

Выберите каким образом задается параллелограмм:

Введите значения векторов: Введите координаты трех любых вершин параллелограмма:

Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах

Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах

• Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.

Теория. Площадь параллелограмма построенного на векторах.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Площадь параллелограмма, построенного на векторах – формула и примеры решения задач

Четырехугольник и вектор на плоскости

Каждый школьник понимает, что параллелограмм является специальным видом плоских четырехугольников. Эта фигура состоит из двух пар параллельных пересекающихся отрезков. Она обладает следующими важными свойствами:

• ее противоположные стороны и углы равны друг другу;
• сумма всех четырех углов составляет 360 градусов;
• если просуммировать лишь два смежных (прилежащих к одной стороне) угла, то получится значение 180 градусов;
• любая диагональ делит фигуру на две равные части (треугольники);
• пересечение диагоналей происходит в точке, которая является геометрическим и массовым центром параллелограмма;
• любая секущая, которая проходит через геометрический центр, делит фигуру на две равные по площади части.

Специальные типы

Исходя из определения параллелограмма, как четырехугольника с параллельными и равными по длине противоположными сторонами, можно привести несколько видов фигуры, которые обладают высокой симметрией по отношению к ряду элементарных операций. Это следующие геометрические типы:

1. Квадрат. Все четыре стороны его равны по длине между собой, а углы составляют 90 градусов. Он является фигурой с достаточно высокой симметрией, и его площадь вычисляется просто как квадрат длины любой его стороны.
2. Прямоугольник. Еще один вид параллелограмма, все углы которого являются прямыми. Его симметрия несколько ниже, чем у квадрата, поскольку длины сторон равны лишь попарно. Площадь фигуры можно вычислить, перемножив длины смежных сторон.
3. Ромб. Специальный геометрический тип параллелограмма, который характеризуется тем, что длины всех его сторон являются одинаковыми. Углы фигуры попарно равны и отличаются от 90 градусов (два тупых и два острых).

Направленные отрезки и операция умножения

Площадь параллелограмма через векторы рассчитать легко, если знать понятие направленного отрезка и уметь работать с соответствующими математическими операциями. Поскольку любая точка на плоскости может быть представлена в виде набора двух координат в декартовой прямоугольной системе, то для P и Q можно записать:

P (x1, y1); Q (x2, y2).

Где числа x1, y1, x2 и y2 являются соответствующими координатами для точек P и Q по осям абсцисс и ординат. Чтобы получить вектор PQ-, который будет направлен из P в точку Q, необходимо из координат Q попарно вычесть значения для P:

PQ- = Q — P = (x2-x1, y2-y1).

Координаты направленного отрезка на плоскости определяются так же, как и для точки, набором из двух чисел. Чтобы построить такой вектор в системе координат, необходимо его начало расположить в точке (0, 0), а конец со стрелкой будет располагаться в точке (x2-x1, y2-y1). Из этой геометрической интерпретации следует, что существует бесконечное множество направленных отрезков, которые эквивалентны между собой. Получаются они друг из друга с помощью параллельного переноса по всей плоскости координат.

Как и числа, направленные отрезки также можно складывать между собой, вычитать и умножать. Рассматривая вопрос построение параллелограмма на векторах и нахождения его площади, необходимо изучить свойства векторного произведения. Оно представляет собой вектор, перпендикулярный плоскости, в которой лежат исходные направленные отрезки. Пусть a- и b- необходимо умножить векторно. Результатом произведения будет следующий вектор c-:

c- = [a-*b-] = |a-|*|b-|*sin (alfa).

Здесь alfa — угол между a- и b-, а |a-| и |b-| – длины соответствующих направленных отрезков.

Направление c- принято определять с помощью правила правой руки. Оно гласит: если четыре пальца ладони направить от конца первого умножаемого вектора к концу второго, то оттопыренный большой палец укажет направление результирующего векторного умножения.

Координаты вектора c- можно вычислить также, если воспользоваться понятием определителя матрицы. Пусть a- имеет координаты (a1, a2), а b- = (b1, b2), тогда формула для определения c- запишется в следующем виде:

c- = (0, 0, (a1*b2-b1*a2)).

Вектор c- имеет первые две нулевые координаты, поскольку он перпендикулярен плоскости, в которой находятся a- и b-.

Формула площади из геометрии

Чтобы получить формулу площади параллелограмма на векторах, необходимо вспомнить, как рассчитывается эта величина для треугольника. Если известна одна сторона (основание a) и высота, которая на нее опущена (h), то получается простое выражение:

Где S3 — площадь треугольника. Поскольку две таких плоских фигуры, которые соединены одной из своих сторон, образуют четырехугольник-паралелограм, то для него рассмотренную величину можно вычислить по формуле:

Пусть вторая сторона параллелограмма равна b, тогда с высотой h она связана через определение тригонометрической функции синус:

sin (alfa) = h/b => h = b*sin (alfa).

Если подставить это равенство в выражение для S4, то нахождение площади фигуры сведется к расчету произведения двух его смежных сторон и синуса угла между ними:

Поскольку угол alfa изменяется от 0 до 180 градусов, то функция синус всегда имеет положительное значение. Этой формулой часто пользуются на практике. Распространение инженерных калькуляторов позволяет быстро и с высокой точностью вычислять синусы любых углов.

Построение параллелограмма

Определить площадь четырехугольника с попарно параллельными сторонами можно не только через длины его сторон. Если внимательно посмотреть на формулу для S4, то можно заметить, что она идентична по виду векторному произведению направленных отрезков.

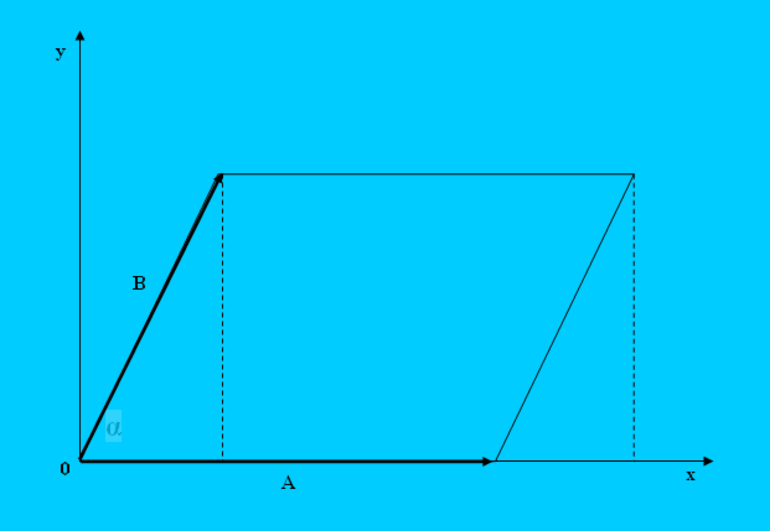
Пусть имеется два вектора a- и b-. Угол между ними равен alfa. Если их начала совместить в одной точке на плоскости, затем, от конца a- продолжить вектор b-, а из b- начертить a-, то получится параллелограмм, побудованый на a- и b-. Очевидно, что модуль векторного произведения этих направленных отрезков будет равен площади полученной фигуры:

S4 = a*b*sin (alfa) = |[a-*b-]|.

Применяя координатное выражение этого произведения, можно записать следующую формулу для площади:

Где a- = (a1,a2) и b-=(b1,b2). Знак модуля необходим потому, что по правилу правой руки могут получаться отрицательные векторы. Площадь же является всегда величиной положительной.

Преимущество последней записанной формулы для S4 по сравнению с выражением, где необходимо знать длины и углы, заключается в том, что ее использование не требует никаких предварительных вычислений. Достаточно лишь знать координаты конца и начала образующих параллелограмм векторов.

Задача с тремя точками

Чтобы научиться пользоваться записанной простой формулой, следует решить простую задачу. Имеется три точки, координаты которых следующие:

На вершинах этих точек следует построить параллелограмм, а затем, рассчитать его площадь S4.

Задачу проще всего решать через использование векторов. Выберем произвольную точку из трех заданных. Пусть это будет A. Из нее выходит два вектора: AB- и AC-. Их координаты определяются таким образом:

AB- = (2−1, 0-(-1)) = (1, 1); AC- = (-4−1, 3- (-1)) = (-5, 4).

Чтобы определить площадь параллелограмма на этих векторах, следует применить формулу для их векторного произведения. Порядок умножения направленных отрезков не имеет значения. Получается следующий результат:

S4 = [AB-*AC-] = 1*4 — (-5)*1 = 9.

Результат получен в единицах квадратных соответствующей двумерной системы координат.

Если была выбрана в качестве исходной не точка A, а B или C, то получился бы тот же результат, что можно доказать, проделав аналогичные вычисления.

Диагонали фигуры

Некоторые задачи по геометрии параллелограммов в качестве начального условия предлагают знание одной или двух его диагоналей. По этим данным необходимо вычислить характеристики всей фигуры, включая ее площадь. Решать такие задачи также удобно с использованием понятия векторов.

Если дана диагональ, выраженная вектором f- и основание, представленное направленным отрезком a-, то формула для площади параллелограмма имеет вид:

Где beta — угол между a- и f-. Видно, что это выражение не отличается от предыдущих для S4. Доказать его справедливость несложно, если рассмотреть построенные на указанных векторах треугольники и использовать признаки их подобия.

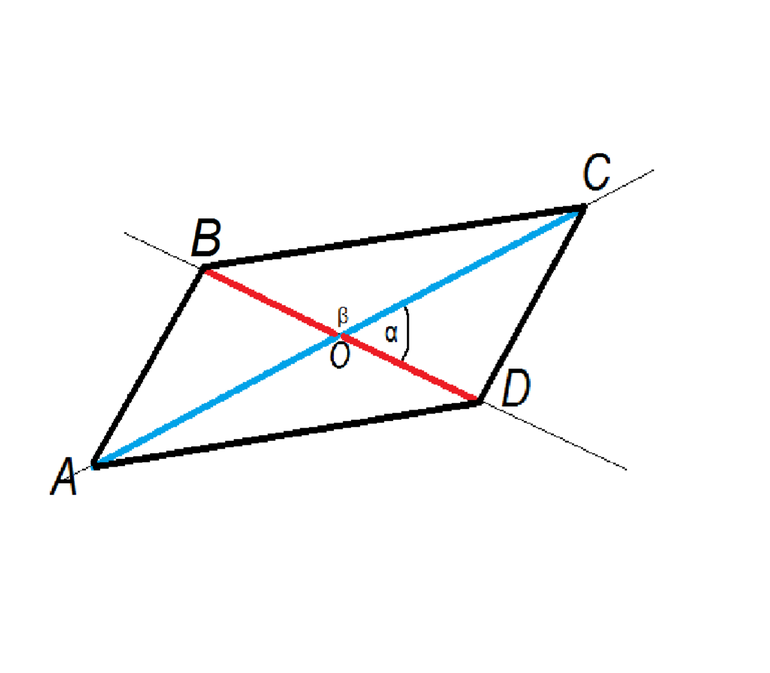
Другой случай, когда даны обе диагонали параллелограмма f- и e-. Воспользовавшись геометрическими построениями на плоскать, можно показать справедливость следующего выражения:

Здесь teta — это угол пересечения e- и f-. Таким образом, чтобы вычислить площадь параллелограмма, диагоналями которого служат вектора, следует вычислить половину модуля их векторного произведения.

Пример решения

Все разнообразие задач на определение площади параллелограмма сводится к знанию единственной формулы векторного произведения. Пусть известны две диагонали фигуры. Они имеют координаты:

Чтобы определить величину S4, достаточно без промежуточных вычислений воспользоваться формулой векторного произведения заданных направленных отрезков:

В связи с развитием интернета, всегда можно использовать калькулятор-онлайн для расчета величины S4. Соответствующий электронный ресурс можно знайти, воспользовавшись любой поисковой системой в браузере.

Трехмерное пространство

В пространственной системе координат каждый вектор задается тремя числами, поэтому их векторное произведение c- также будет представлять набор трех цифр. Построенный в пространстве параллелограмм на двух векторах будет иметь площадь, равную длине направленного отрезка c-. Для расчета его модуля следует использовать известное выражение: сумма квадратов трех координат под корнем.

Таким образом, площадь параллелограмма проще всего вычислять, используя операцию умножения векторов. Этот метод является универсальным не только для задач на плоскости, но и для решения проблем в трехмерной системе координат.

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/assistance/vector/parallelogram_area/

http://nauka.club/matematika/geometriya/ploshchad-parallelogramma-postroennogo-na-vektorakh.html

[/spoiler]

Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.

Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье площадь параллелограмма. Площадь будет равняться произведению модулей на синус угла между ними:

Рассмотрим пример расчета площади параллелограмма построенного на векторах.

Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.

Расчет длин сторон фигуры, заданной координатами

Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a(x1;y1;z1), а вектора b(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:


Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.

Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.

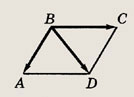
Можно ли на векторах AB и AD построить параллелограмм?
Если да, найти длины сторон параллелограмма
Значения: A(1,1,1), B(0,1,0) D(0,2,1)

Векторы. Метод
координат

• Вектором называется направленный
отрезок. Длиной вектора называется длина этого отрезка. Два вектора называются
равными, если равны их длины и векторы одинаково направлены.
Если А — начало, а Б — конец вектора, то такой вектор обозначается символом

а его длина —

Пусть в фиксированной прямоугольной
системе координат Охуz заданы координаты начала и конца вектора

Тогда числа X = х₂
– x₁
Y = у₂ – y₁, Z = z₂ – z₁ являются
координатами вектора

в этой системе координат.
Употребляется запись:

Векторы с координатами

называются ортами координатных
осей: Ох (оси абсцисс), Оу (оси ординат) и Oz (оси аппликат).
Если

то справедливо равенство

которое называется разложением
вектора

по ортам координатных осей.

Все равные между собой
векторы имеют одинаковые координаты. Равные векторы отождествляются (т.е. считаются
одним вектором, начало которого можно поместить в любую точку) и обозначаются
одной буквой:

Если

Если же

называется нулевым вектором;

Для любой napы векторов

определены их сумма

Любой вектор

можно умножить на любое
число

Сумму и разности векторов

можно найти по правилу
параллелограмма

Вектор

он направлен одинаково
с вектором

при k > О и противоположно
— при k < О.

При этом

Наконец, если

Используя приведенные сведения,
решите следующие задачи (1—14):

Задание 1.

Пусть заданы координаты
точек А и Б. Найдите координаты и длину вектора

если:

Ответ:

Задание 2.

Дан вектор

Найдите координаты и длины
векторов:

Ответ:

Задание 3.

Дан вектор

Найдите:

а) координаты точки N, если
М(0; -1; 2);
б) координаты точки М, если N(5; -2; 1);
в) координаты середины отрезка MN, если М(1; 1; 2);
г) координаты середины отрезка МАГ, если N(3; 5; -1);
д) координаты точки С, лежащей на отрезке MN и делящей его в отношении МС :
CN =1:3, если М(0; 0; -1);
е) координаты точки D, лежащей на прямой MN и такой, что MN : ND = 2 : 3, если

Решение

а):

Обозначим координаты точки
N через х, у и z, т.е. N(x, у, z). По определению координат вектора

имеем

в)

Пусть L(x; у; z) — середина
отрезка MN. 1 огда вектор

Следовательно,

Указание d):

Вектор

Ответ:

a) (4; -2; 5)

б) (1;-1;-2)

в)

г) (1; 5,5; -2,5)

д)

е) D(8; -3; 5) или D(-4;
0; -4)

Задание 4.

Даны векторы

Найдите координаты и длины
векторов:

Ответ:

{6; -10; 16}; {-2; -4: 4};
{4; -6; 12}; {-6; 8; -20}

Задание 5.

Даны три последовательные
вершины параллелограммаАБСD: А(-3; -2; 0); B(3; -3; 1) и С(5; 0; 2). Найдите
координаты его четвертой вершины D и длины сторон.

Решение:

Вычислим координаты векторов

и

Тогда вектор

Зная начало В(3; -3; 1)
этого вектора, найдем его конец D)(-1; 1; 1). Длины сторон параллелограмма
равны соответственно

и

Ответ:

Задание 6.

Найдите длины диагоналей
АС и BD параллелограмма ABCD, если А(1; -3; 0); B(-2; 4; -1) и С(-3; 1; 1).

Ответ:

Задание 7.

Треугольник задан координатами
своих вершин А(3; 0; -1); B(-1; 4; 1) и С(5; 2; 3). Найдите длину медианы AD.

Ответ:

Задание 8.

Известны координаты вершин
треугольника: А(-2; -3; 8); B(2; 1; 7); С(1; 4; 5), Найдите координаты точки
пересечения медиан этого треугольника.

Решение:

Пусть D — середина отрезка
ВС. Эта точка имеет координаты D(1,5; 2,5; 6). Точка О пересечения медиан делит
отрезок AD в отношении АО : OD = 2 : 1, т.е. вектор

Зная координаты точки А,
находим координаты точки

Ответ:

Задание 9.

Известны две вершины треугольника
А(2; -3; 5), В(-2; 1; -3) и точка О(1; 2; 3) пересечения его медиан. Найдите
координаты вершины С этого треугольника.

Указание:

Пусть M — середина AB (рис.).

На продолжении ОМ возьмите
точку D так, что ОМ = MD. Четырехугольник AOBD – параллелограмм. Вектор

Найдите координаты вектора

а затем, зная координаты
точки О, — координаты точки С.

Ответ:

C(3; 8; 7)

Задание 10.

Даны точки А( -1; 2; -2)
и B(3; -4; 12). Найдите расстояние от начала координат О до точки D, лежащей
на отрезке АВ и делящей его в отношении AD : DB = = ОА : ОB. Чем является отрезок
OD в треугольнике AОB?

Указание:

AD : DB = 3 : 13

Ответ:

биссектриса.

Задание 11.

Даны вершины треугольника:
А(4; 5; 0); Б(3; 3; -2) и С(2; 2; 6). Найдите точку пересечения стороны ВС и
биссектрисы угла А.

Решение:

Пусть AL — биссектриса треугольника
ABC. Согласно свойству биссектрисы, отношение BL : LC = АВ : АС. Так как,

Зная координаты точки В,
находим С (2,7; 2,7; 0,4).

Ответ:

С (2,7; 2,7; 0,4)

Задание 12.

Точки М₁
и М₂
— середины отрезков A₁В₁
и А₂В₂. Найдите длину отрезка М₁М₂,
если А₁(0; 1; 2),А₂(1; 2; 1), B₁(-1;-1; 3)
и В₂(1; 0; 0).

Ответ:

Задание 13.

Найдите координаты точки
С, лежащей на оси абсцисс и одинаково удаленной от точек А(1; 2; 3) и Б(2; 3;
4).

Решение:

Точка на оси абсцисс характеризуется
тем, что ее вторая и третья координаты равны нулю, т.е. С(х; 0; 0).
Расстояния от точки С до точек А и В равны

и

соответственно. Приравняв
эти расстояния, получим

х² – 2х + 14
= х² – 4х + 29 < =>2х = 15 <=> x = 7,5.

Ответ:

Задание 14.

Найдите координаты точки
М, лежащей на оси абсцисс, если расстояние от М до точки А(1; 2; 1) втрое больше
расстояния до точки B(-7; 1; 2).

Ответ:

М(-10; 0; 0) или М(-6; 0;
0)

• Ненулевые векторы называют
коллинеарными, если они лежат на параллельных прямых, и компланарными, если
они параллельны одной плоскости. Нулевой вектор считается коллинеарным любому
вектору; любые три вектора, среди которых есть нулевой, считаются компланарными.

Векторы

коллинеарны в том и только
в том случае, если найдутся числа x, у (х² + у² # 0) такие,
что

Три вектора

компланарны в том и только
в том случае, если найдутся числа х, у, z (х² + + у² +
z² # 0) такие, что

Если р, q и г — три некомпланарных вектора, то любой вектор а можно представить
в виде а = хр + yq + zr. Это представление называется разложением вектора а
по векторам р, q, г, а числа х, у, г — коэффициентами разложения. Если векторы
р и q не компланарны, то любой вектор а, лежащий в плоскости векторов р и q,
также разлагается по векторам р и q.

Решите следующие задачи
(15—38):

Задание 15.

На плоскости даны два вектора

Разложите вектор

по векторам р и q.

Решение:

Необходимо найти числа х
и у такие, что

Запишем координаты векторов

в столбец

Таким образом, для нахождения
х и у имеем систему линейных уравнений

Ответ:

Задание 16.

Даны векторы

Запишите разложение вектора

векторам

Ответ:

Задание 17.

Разложите вектор

по векторам

Ответ:

Задание 18.

Разложите вектор

по векторам

Ответ:

Задание 19.

Даны точки А(24; -1; -4);
В(-13; 1; -12); С(15; 20; 5); D(2; -1; 1). Разложите радиус-вектор точки, координаты
которой удовлетворяют уравнению 2х – Зу + 4z – 11 = О, по радиус-векторам точек,
координаты которых этому уравнению не удовлетворяют. (Радиусом-вектором точки
А
называют вектор О А , где О — начало координат.)

Решение:

Сначала найдем точку, координаты
которой удовлетворяют уравнению 2х – Зу + 4z – 11 = 0. Непосредственной подстановкой
убеждаемся, что это точка D: 2 • 2 – 3 • (-1) + 4-1-11 = 0.

Таким образом, надо разложить
вектор

по векторам

Чтобы найти числа х, у и
z, для которых

как и при решении задачи
15, получаем систему

Ответ:

Задание 20.

Даны точки А(35, -16; 20);
B(-1; -24; 3); С(-20; 16; -4); D(-1; -4; 2). Разложите радиус-вектор точки,
координаты которой удовлетворяют уравнению 15x + 23y – 17z – 43 = 0, по радиус-векторам
точек, координаты которых этому уравнению не удовлетворяют.

Ответ:

Задание 21.

Вершины пирамиды имеют координаты
А(3; 2; – 8); B(3; 5; 1); С(0; 4; 1); D(1; 2; 3). Разложите вектор

по векторам

Ответ:

Задание 22.

Вершины пирамиды имеют координаты
А(3; -2; 2); В(-1; 3; 1); С(2; -1; -3); D(0; 4; -1). Разложите вектор

по векторам

Ответ:

Задание 23.

При каких значениях х и
у векторы

и

коллинеарны?

Решение:

Векторы

коллинеарны, если существуют
числа

причем хотя бы одно из
этих чисел не равно нулю. Записав координаты векторов в столбец, получаем

Выразив из третьего уравнения

подставим это выражение
в первые два уравнения:

Ответ:

Задание 24.

Даны векторы

Найдите все значения х
и у, при которых эти векторы коллинеарны, но не равны.

Решение.

Два вектора коллинеарны,
если они лежат на параллельных прямых, т.е. один из векторов

равен другому, умноженному
на какое-то число, т.е.

У обоих векторов вторая
координата зависит только от у. Рассмотрим два случая:

1) если у = 0, то векторы
имеют вид

Данные векторы параллельны
только когда х = 0;

2) если

(это вытекает из сравнения
вторых координат этих векторов), откуда

Из второго уравнения находим х = +1. Подставив эти значения х в первое уравнение,
получаем

Ответ:

{(±1; -2); (+1; -1); (0;
0)}

Задание 25.

Даны векторы

Найдите все значения р и q, при которых эти векторы коллинеарны, но не равны.

Ответ:

{(±1; + 1); (0; 0)}

Задание 26.

Проверьте, что векторы

компланарны.

Решение:

Три вектора компланарны,
если существуют одновременно не равные нулю числа х, у и z такие, что

т.е. система

имеет ненулевое решение.
В качестве такого решения можно взять, например, х = 0, у = 3, z = 4. Таким
образом, векторы компланарны.

Задание 27.

Проверьте, что точки А(1;
2; -1), В(0; 1; 5), С(-1; 2; 1), D(2; 1; 3) лежат в одной плоскости.

Указание.

Покажите, что векторы

компланарны.

Задание 28.

Найдите значение х, при
котором вектор

разлагается по векторам

Решение.

Будем искать числа

такие, что

Получим систему уравнений

откуда

а тогда из первого уравнения
находим, что х = -11.

Ответ:

-11

Задание 29.

Найдите значение у, при
котором вектор

разлагается по векторам

Ответ:

6

Задание 30.

При каком значении х векторы

компланарны, если:

Ответ:

а) 2; б) 3

Задание 31.

Пусть К и М — середины сторон
ВС и CD параллелограмма

Выразите векторы

Решение.

Выражая векторы

через

получаем

откуда

Теперь легко находим:

Ответ:

Задание 32.

В параллелограмме ABCD точка
М лежит на стороне ВС, причем ВМ : МС = 1:2, точка N — на стороне

Выразите векторы

Ответ:

Задание 33.

Пусть О — точка пересечения
медиан треугольника

Разложите векторы АВ и
ВС по векторам

Ответ:

Задание 34.

Векторы

лежат в одной плоскости
и образуют друг с другом углы

Разложите вектор

по векторам

Ответ:

Задание 35.

К графику функции

проведена касательная в
точке А(х₀ ;
у₀ ) с
абсциссой х₀
= 2. Эта касательная пересекает ось абсцисс в точке С, а ось ординат — в точке
В. Разложите вектор

Решение.

Ордината у₀
точки А равна 8, т.е., записав
уравнение касательной к кривой

в этой точке, получаем у
= х + 6.

Теперь вычислим координаты
точек В(0; 6), С(-6; 0) и нужных нам векторов:

и

Найдем числа х и у такие,
что

откуда {6; 0} = x {-2; -2}
+ y {2; 8}.

Решив полученную систему,
находим х = -4 , у = -1.

Ответ:

Задание 36.

Из точки А(2; 0) к графику
функции у = х² – 2х + 1 проведены две касательные. Пусть B и С —
точки касания, причем точка B лежит на оси абсцисс. Разложите вектор

Решение:

Уравнение пучка прямых,
проходящих через точку А(2; 0) (рис.)

имеет вид у = k(x – 2).
В точках касания должны выполняться равенства

откуда х₁ = 1,
k₁ = 0; Х₂ = 3, k₂ = 4. Следовательно,

Отсюда получаем, что

Ответ:

Задание 37.

Парабола у = х²
– 4х + 2 пересекается с прямой у = х + 8 в точках А и B. Касательная к этой
параболе в точке М(х₀; у₀), где х₀ = 3, пересекается
с той же прямой в точке С. Разложите вектор

если D — вершина данной
параболы.

Ответ:

Задание 38.

Начало А(х₀;
y₀) вектора АВ лежит на графике функции

где х₀ — точка
минимума этой функции. Конец В вектора

лежит на прямой 2х – у
+ + 2=0 так, что вектор

имеет наименьшую возможную
длину. Найдите координаты вектора

если вектор

в 3 раза длиннее вектора

и коллинеарен ему.

Решение.

Найдем минимум функции

Имеем

При переходе через эту
точку знак производной меняется с минуса на плюс, т.е. х = 4 — минимум; зна-
чение функции

Таким образом, началом
вектора

является точка А(4; 5).
Далее, точка на прямой 2х – у + 2 = О имеет координаты B(t; 2t + 2). Теперь
запишем квадрат длины вектора

Эта величина достигает минимума при t = 2. Значит, концом вектора

служит точка В(2; 6), а
вектор

Вектор, колли-неарный вектору

и по длине в 3 раза больший,
чем

имеет вид

Ответ:

• Рассмотрим понятие скалярного
произведения векторов. Отложим от произвольной точки О векторы

Углом между ненулевыми
векторами

называется угол между лучами
ОА и ОB. Обозначение:

Скалярное произведение
векторов

определяется равенством

Если хотя бы один из векторов нулевой, то скалярное произведение считается равным
нулю. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда,
когда эти векторы перпендикулярны.

Скалярное произведение
обладает следующими свойствами:

Из свойства (4) получаем формулы:

Последняя формула позволяет находить углы между векторами.

Задание 39.

Найдите скалярное произведение
векторов

если:

Ответ:

Задание 40.

Найдите угол между векторами

если:

Решение в).

Имеем

откуда

Ответ:

в)

Задание 41.

Вычислите внутренние углы
треугольника ABC, где А(1; 2; 1), В(3; -1; 7), С(7; 4; -2). Является ли этот
треугольник равнобедренным?

Ответ:

Треугольник равнобедренный.

Задание 42.

При каком значении а векторы

перпендикулярны?

Ответ:

a = -6

Задание 43.

Покажите, что точки А(1;
-1; 1), В(1; 3; 1), С(4; 3; 1), .0(4; -1; 1) являются вершинами прямоугольника.

Решение.

Находим векторы:

и

Так как

то ABCD — прямоугольник.

Задание 44.

Векторы

являются смежными сторонами
параллелограмма. Определите угол между его диагоналями.

Указание.

Диагоналями параллелограмма
служат векторы:

Найдите эти векторы и угол
между ними.

Ответ:

Задание 45.

Заданы три вершины параллелограмма:
А(2; 1; 3), В(5; 2; -1), С(-3; 3; -3). Найдите угол между его диагоналями АС
и BD.

Ответ:

Задание 46.

Известны вершины тр. АВС:
А(2; -3; 0), В(2; -1; 1), С(0; 1; 4). Найдите угол между медианой BD и основанием
АС.

Ответ:

Задание 47.

Найдите вектор

коллинеарный вектору

и удовлетворяющий условию

где

Решение.

Будем искать вектор

Для нахождения t имеем уравнение

т.е.

Ответ:

Задание 48.

Даны векторы

Найдите вектор

если он перпендикулярен
вектору

и удовлетворяет условиям

Указание.

Вектор

перпендикулярный вектору

Ответ:

{2; -3; 0}

Задание 49.

Найдите вектор

зная, что он перпендикулярен
векторам

и удовлетворяет условию

Ответ:

{3; -3; -3}

Задание 50.

Найдите вектор

если известно, что векторы

компланарны,

Указание.

Так как векторы

компланарны, то

Ответ:

Задание 51.

Даны векторы

Найдите единичный вектор,
лежащий в плоскости векторов

и образующий угол

Ответ:

• При решении задач полезно уметь записывать уравнение прямой на плоскости,
проходящей через данную точку М(х₀ ;
у₀ ) перпендикулярно
данному вектору

а также уравнение прямой,
проходящей через данную точку М(х₀ ;
у₀ ) в
направлении данного вектора е = {m; n}.

Эти уравнения соответственно
имеют вид

Вектор

называется нормальным вектором
прямой l (или нормалью), а

— направляющим вектором
прямой l.

Уравнение плоскости, проходящей
через точку М(х₀; у₀; z₀), перпендикулярно
вектору

(вектору нормали):

Если уравнение плоскости записано в общем виде, т.е. ах + by + cz + d =0 (для
прямой на плоскости ах + by + d = 0), то вектор

— это нормаль к плоскости
(нормаль к прямой на плоскости).

Уравнения прямой в пространстве,
проходящей через точку М(х₀ ;y₀;
z₀) в направлении вектора

имеют вид

Используя формулы (1—4), решите следующие задачи (52—60):

Задание 52.

Запишите уравнение прямой
на плоскости, если эта прямая проходит через:

а) точку М( 1; -1) перпендикулярно
вектору

б) точку М(3; -2) перпендикулярно
вектору

где А(3; 2), В(-1; 5);

в) точку М(0; 5) в направлении
вектора

г) точки М(1; 3) и N(-2;
4);

д) точку М(-1; 2) параллельно
прямой x – 2y + 3 = 0;

е) точку А(2; 1) параллельно
прямой, проходящей через точки В(3; 1) и С(-4; 0);

ж) точку пересечения прямых
2х + 5у -8 = 0, х – 3у – 4 = 0 и начало координат.

Решение.

г) Надо записать уравнение
прямой, проходящей через точку М(1; 3), а направляющий вектор этой прямой

имеем

Указание.

д) Нормальный
вектор искомой прямой такой же, как и у данной прямой, т.е. n = {1; -2}.

Ответ:

а) – х + 2у + 3 = 0
б) -4х + Зу + 18 = 0
в) х + у – 5 = 0
г) x + Зу – 10 = 0
д) х – 2у + 5 = 0
е) х – 7у + 5 = 0
ж) у = 0
з) АВ : Зх + 5y+ 4 = 0; ВС : Зх – 5у + 14 = 0; CD : х = 7; AD : Зх – 5у – 16
= 0; BС и AD параллельны.

Задание 53.

Даны координаты вершин четырехугольника:
А(2; -2), B(-3; 1), С(7; 7), D(7; 1). Запишите уравнения его сторон. Проверьте,
что это трапеция.

Решение.

г) Найдем вектор

перпендикулярный векторам

(т.е. нормальный вектор
искомой плоскости). Этот вектор должен удовлетворять системе уравнений

Пусть

Таким ооразом, одним из
решении системы является вектор

(координаты остальных решений
пропорциональны данному). Искомое уравнение имеет вид

1 • (x – 3) + 4 • (х –
4) + 7 • (z + 5) = 0 <=> х + 4y + 7z + 16 = 0

Указание.

д) Искомая плоскость параллельна
нормальным векторам двух данных плоскостей, т.е. векторам,

Ответ:

а) x + 2у + 3z = 0
б) 3x + 4y + 6z – 29 = 0
в) 2х + 2у – z – 5 = 0
г) х + 4y + 7z + 16 = 0
д) 1х – у – 5г = 0

Задание 54.

Запишите уравнение плоскости,
если она проходит через:

а) начало координат перпендикулярно
вектору

б) точку А(1; 2; 3) перпендикулярно
вектору

где B(4; 6; 9);

в) точку А(2; 1; 1) параллельно
плоскости 2х + 2у –z + 4 = 0;

г) точку М(3; 4; -5) параллельно
двум векторам

д) начало координат перпендикулярно
двум плоскостям

2x – y + 3z – 1 = 0 и x
+ 2y + 2=0

Указание.

б) Направляющим вектором
данной прямой является вектор АВ

г) Направляющий вектор
прямой перпендикулярен нормальным векторам двух данных плоскостей (см. решение
задачи 53, г).

Ответ:

Задание 55.

Запишите уравнения прямой
в пространстве, если она проходит через:

а) точкуА(1; 2; 3) в направлении
вектора

б) точки А(-1; 2; 3) и
Б(2; -1; 1);

в) точку А(2; 3; 0) перпендикулярно
плоскости

х – у + 2z – 1 = 0;

г) начало координат параллельно
линии пересечения плоскостей 2х – 5у + z – 3 = 0 и х + 2у -z + 2 = 0.

Решение.

Запишем уравнения прямой

Если приравнять данные
отношения числу t, то получим параметрические уравнения прямой:

Подставив выражения в уравнение плоскости, найдем t:

2(5t – 3) + 2(-3 + 4) –
t + 4 = 0 <=> 3t + 6 = 0 <=> t = -2

Теперь подставим это значение
t в систему и получим координаты искомой точки:

Ответ:

(-13; 10; -2)

Задание
56.

Найдите координаты точки
пересечения плоскости 2х + 2у – z + 4 = 0 и прямой, проходящей через точки А(-3;
4; 0), В(2; 1; 1).

Указание.

Найдите значение параметра,
при котором направляющий вектор прямой перпендикулярен нормальному вектору плоскости.

Ответ:

m = -3

Задание
57.

При каком значении m прямая

параллельна плоскости х
– Зу + 6z + 7 = 0?

Указание.

Найдите точку пересечения
плоскости и прямой, перпендикулярной плоскости и проходящей через точку Р.

Ответ:

(1; 4; -7)

Задание
58.

Найдите координаты проекции
точки Р(5; 2; -1) на плоскость 2х – у + Зz + 23 = О.

Ответ:

Q(-5; 1; 0)

Задание
59.

Найдите координаты точки
Q, симметричной точке Р(1; 3; -4) относительно плоскости Зx + у – 2z = 0.

Замечание.

Нуль в знаменателе означает,
что третья координата любой точки прямой равна -2.

Ответ:

Задание
60.

Даны вершины

и С(4; -7; -2). Запишите
уравнение медианы, проведенной из вершины С.

Указание.

Пусть

Тогда

— направляющий вектор искомой
биссектрисы.

Ответ:

Задание
61.

Даны вершины

С(-5; 14; -3). Запишите
уравнение биссектрисы угла при вершине В.

Решение.

а) Угол между прямыми на
плоскости равен либо углу между направляющими векторами данных прямых (рис.
а)

либо дополняющему этот угол
до 180° (рис. б). В обоих случаях

По условию,

Ответ:

a)

б)

• Углы между прямыми на
плоскости и в пространстве, между плоскостями, а также между прямой и плоскостью
находим, рассматривая соответствующие направляющие векторы прямых и нормальные
векторы плоскостей.

Задание
62.

Найдите угол между прямыми
на плоскости:

г) l₁
и l₂ ,
если l₁
— высота

опущенная из вершины А,
а l₂ —
медиана того же треугольника, проведенная из вершины В, где А(1; -1), В(-2;
1), С(3; 5).

Указание.

Косинус угла между плоскостями
равен модулю косинуса угла между нормальными векторами.

Ответ:

m = -1

Задание
63.

При каком значении m плоскость
2х + mу – Зz –1 = 0 перпендикулярна плоскости 5х + у + Зz + 1 = 0?

Ответ:

Задание
64.

Найдите угол между плоскостью
Оху и плоскостью

Ответ:

Задание
65.

Найдите угол между плоскостями

Ответ:

Задание
66.

Чему равен двугранный угол,
образованный плоскостями x + 2y – z – 1 = 0 и 2x + y – z – 2 = 0?

Решение.

Синус угла

между прямой и плоскостью
(рис.)

равен модулю косинуса угла
между направляющим вектором

прямой и нормальным вектором

плоскости, т.е.

В данном случае

откуда

Точку пересечения прямой
и плоскости найдем так же, как и в задаче 55.

Ответ:

a)

б) Прямая параллельна плоскости.

Задание
67.

Найдите угол между прямой
и плоскостью, а также координаты точки пересечения этой прямой и плоскости:

Ответ:

Задание
68.

Даны точки А(1; -1; 1) и
В( – 3; 2; 1). Найдите угол между прямой, проходящей через точки А и B, и плоскостью
6х + 2у – Зz – 7 = 0.

Решение.

а) Найдем уравнения прямой,
проходящей через точку М перпендикулярно плоскости. Ее направляющий вектор совпадает
с нормальным вектором плоскости (2; -1; 2). Значит, уравнение прямой имеет вид

Приравняв эти отношения
числу t, получим параметрические уравнения прямой

Подставим выражения для х, у и z в уравнение плоскости:

2(2t – 2) – (-t – 4) + 2(2t
+ 3) + 3 <=> t = -1.

Подставив это значение
t в систему, найдем точку пересечения прямой и плоскости (проекцию точки М на
плоскость): М'(-4; – 3; 1). Расстояние от М до М’ является искомым:

д) Запишем уравнение плоскости,
проходящей через точку Р и перпендикулярной данной прямой:

3(х – 1) + 2(у + 1) – 2(z
+ 2) = 0 <=> Зх + 2у – 2z – 5 = 0.

Найдем точку пересечения
данной прямой и полученной плоскости: Р'(3; 2; 4). Искомое расстояние — это
расстояние между точками Р и Р’.

Указание.

в) Найдите расстояние от
плоскости х – 2у – 2z — 12 = 0 до какой-нибудь точки плоскости х – 2у— 2z –
6 = 0 (например, до точки М(6; 0; 0));

Ответ:

a) {3}
б) {1}
в) {2}
г)

д) {7}

e) {21}

Задание
69.

Вычислите расстояние:

а) от точки М(-2; -4; 3)
до плоскости 2х – у + 2z + 3 = 0;

б) от точки М(2; -1; -1)
до плоскости 16x – 12у + 15z – 4 = 0;

в) от плоскости х – 2у
– 2z – 12 = 0 до параллельной ей плоскости х – 2у – 2z – 6 = 0;

г) от середины отрезка
М₁ М₂
до плоскости 5х – 2у + z
– 1 = 0, где M₁ (1;
4; -3), М₂ (2;
5; 0);

Решение.

Точка A'(3; -4; -7) симметрична
точке А относительно плоскости Оху (рис.).

Уравнения прямой, проходящей
через точки А’и В, имеют вид

Эта прямая пересекается с плоскостью Оху в точке

которая и является искомой
точкой (для нахождения ее координат достаточно в уравнениях прямой положить
я = 0).

Докажем, что эта точка
удовлетворяет условию задачи.

Возьмем на плоскости любую
другую точку Р. Так как АР + ВР = А’Р + ВР = А’В, AQ + BQ = A’Q + BQ и A’Q +
BQ > А’ В (сумма двух сторон треугольника больше третьей стороны), то АР
+ ВР < AQ + BQ, что и требова лось доказать.

Ответ:

Задание
70.

На плоскости Оху найдите
такую точку Р, сумма расстояний от которой до точек А(3; -4; 7) и B(-5; -14;
17) была бы наименьшей.

Ответ:

Р(-2; -2; 5)

Задание
71.

На плоскости 2х – Зу + 3z
= 17 найдите такую точку Р, сумма расстояний от которой до точек А(3; -4; 7)
и В(-5; -14; 17) была бы наименьшей.

Ответ:

а) (х – 1)² +
(у – 2)² + (2 – З)² = 16;
б) (х + 1)² + (у – 2)² + (2 – 2)² = 9;
в) х² + у² + z² = 25.

• Уравнение сферы с центром в точке А(х₀ ;
у₀ ; z₀)
и радиусом R имеет вид

(X – Х₀)²
+ (у – У₀)² + (z – z₀)² = R².

Задание
72.

Запишите уравнение сферы:

а) с центром в точке А(1;
2; 3) и радиусом R = 4;
б) с центром в точке А( -1; 2; 2), проходящей через начало координат;
в) с центром в точке О(0; 0; 0), касающейся плоскости 2х + 2у – z + 15 = 0.

Ответ:

(х – З)² + (у
+ 1)² + (z – 1)² = 21.

Задание
73.

Запишите уравнение сферы,
если точки А(2; -3; 5) и B(4; 1; -3) являются концами одного из ее диаметров.

Решение.

а) Так как z²
– 6z = z² – 6z + 9 – 9 = (z – З)² – 9, то уравнение сферы
запишется следующим образом:

х² + у²
+ (2 – З)² = 9.

Ответ:

a) (0; 0; 3); 3
б) (0; -10; 0); 10
в) (2; 1; -1); 5

Задание
74.

Определите координаты центра
сферы и ее радиус, если сфера задана уравнением:

а) х² + у²
+ z² – 6z = 0;
б) х² + у² + z² + 20у = 0;
в) х² + у² + z² – 4x – 2у + 2z – 19 = 0.

Решение.

Координаты произвольной
точки Q, лежащей в данной плоскости, имеют вид (х; у; 2х + у + 3). Неизвестные
х и у можно найти, приравняв квадраты расстояний |QM₁|²
= |QM₃|² и |QM₂|² = = |QM₃|²,
т.е.

Таким образом, получаем точку Q(1; -2; 3). Радиус сферы равен |QM₁|
= 7.

Ответ:

(х – 1)² + (у
+ 2) + (z – З)² = 49.

Задание
75.

Запишите уравнение сферы,
если она проходит через точки M₁ (3; 1; -3), М₂(-2; 4;
1), М₃(-5; 0; 0), а ее центр лежит в плоскости 2x + y – z + 3 = 0.

Указание.

Искомое расстояние равно
разности расстояния от центра сферы до плоскости и радиуса сферы.

Ответ:

2

Задание
76.

Найдите расстояние от плоскости
х + 2у – 2z – 15 = 0 до сферы х² + у² + z²
– 9 = 0.

Решение.

Введем систему координат
Оху так, чтобы А(0; 0), В(0; За), D(a; 0), где а — длина стороны прямоугольника
(рис.).

Пусть N(x; у). Тогда |АN|²
= -х² + у² = 2; |BN| = х² + (у – За)²
= 32, |DN|² = (х – а)² + у² = 4.

Приходим к системе уравнений:

Уравнения второй системы получены вычитанием второго уравнения первой системы
из первого, умноженного на 2, и третьего — из первого, умноженного на 16. Вторая
система — однородная. Полагая

имеем

Подставляя v = 5u – 1 в
первое уравнение, легко находим

Так как

то из уравнения х²
+ у² = 2 получим

Теперь вычислим площадь прямоугольника:

Далее, поскольку

имеем

откуда

Ответ:

• Введение декартовой системы координат на плоскости или в пространстве довольно
часто позволяет сводить решение геометрических задач к приведенным ниже стандартным
вычислительным задачам (вычислению чек пересечения плоскостей и прямых, углов
между прямыми и плоскостями и т.д.) В этом и заключается суть координатного
метода решения геометрических задач.

Введя подходящим образом
систему координат, решите следующие задачи (77—108):

Задание
77.

В прямоугольнике ABCD сторона
АВ втрое длиннее стороны БС. Внутри прямоугольника лежит точка N,
причем

Найдите угол BAN и площадь
прямоугольника ABCD.

Ответ:

Задание
78.

В прямоугольнике ABCD сторона
AD вдвое длиннее стороны АВ. Внутри прямоугольника расположена
точка М, причем

Найдите угол АВМ и площадь
прямоугольника ABCD.

Ответ:

Задание
79.

В прямоугольном треугольнике
ABC длины катетов равны сооветственно 8 и 6. Прямая AD делит сторону ВС в отношении
BD : DC = 4:5. Найдите угол между прямыми АВ и AD.

Решение.

Расположим систему координат
так, чтобы А(-6; 0), С(6; 0), а точка В лежала на оси Оу (рис.).

Тогда

Теперь находим

а тогда

Ответ:

Задание
80.

В равнобедренном треугольнике
ABC (|АВ| = |ВС| = 8) точка ? делит боковую сторону АВ в отношении 3:1, считая
от вершины В. Найдите угол между прямыми СЕ и СА, если |СА| = 12.

Решение.

Выберем систему координат
Оху так, чтобы ее центр совпал с центром вписанной в квадрат окружности, оси
координат были параллельны сторонам квадрата, а точка Е лежала на оси Ох и имела
координаты

Тогда:

— уравнение окружности;

– уравнение прямой (АЕ).

Находим координаты точки
F пересечения прямой АЕ и окружности. Получаем

откуда

Теперь найдем

Ответ:

Задание
81.

В квадрат ABCD со стороной
а вписана окружность, которая касается стороны CD в точке Е. Найдите длину хорды,
соединяющей точки, в которых окружность пересекается с прямой АЕ.

Ответ:

Задание
82.

На плоскости лежит равнобедренный
прямоугольный треугольник, у которого катет имеет длину а. Поворотом в этой
плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается
другой равнобедренный прямоугольный треугольник. Найдите площадь четырехугольника,
являющегося общей частью этих двух треугольников.

Решение.

Выберем систему координат
Оху так, чтобы вершина, вокруг которой производится поворот, совпала с началом
координат, а стороны лежали на координатных осях (рис).

Пусть ОВСD – исходный квадрат,
тогда В(0;а), С(а;а), D(а;0), а координаты точки D₁ (образа точки
D при повороте) таковы:

D₁ (a cos 30°;
а sin 30°). т.е.

Уравнение прямой (OD₁):

уравнение прямой (С₁D₁) :

т.е.

Прямые (C₁D₁) и (ВС) пересекаются в точке

Тогда

Следовательно, периметр
четырехугольника

Ответ:

Задание 83.

На плоскости лежит квадрат
со стороной длины а. Поворотом в этой плоскости квадрата вокруг одной из его
вершин на угол в 30° получается другой квадрат. Найдите периметр четырехугольника,
являющегося общей частью этих двух квадратов.

Ответ:

Задание 84.

В вершинах квадрата расположены
центры кругов радиуса

Найдите длину стороны квадрата,
если площадь общей части всех кругов, лежащей внутри квадрата, равна

Решение.

Расположим систему координат
Охуz так, чтобы ос нование пирамиды лежало в плоскости Оху, оси Ох и Оу были
параллельны сторонам основания, а вершина S лежала в верхнем полупространстве
(рис.).

Пусть

Согласно условию имеем

а нужно найти

Мы видим, что

Такимобразом,

Ответ:

Задание
85.

В четырехугольной пирамиде
SABCD основание ABCD — прямоугольник, SA = 2, SB = 3, SC = 4. Найдите длину
SD.

Указание.

Центр описанной около треугольника
ABC окружности лежит на середине гипотенузы АС.

Ответ:

Задание
86.

В четырехугольной пирамиде
SABCD угол BCD треугольника основания — прямой, SB = 4, SC = 5, SD = 6. Найдите
расстояние от вершины S до центра описанной около треугольника BCD окружности,
если длина гипотенузы

Решение.

Выберем следующую систему
координат (рис.):

Начало координат совпадает
с точкой Р, ось Рх параллельна основаниям, ось Ру перпендикулярна Рх и лежит
в плоскости трапеции, ось Р₁ перпендикулярна плоскости трапеции.
Обозначим высоту трапеции через А. Вычислим координаты точек P₁(0;
0; 1), S₁(4; 0; 1), Q₁(1,5; h; 7), R₁(2,5;
А; 2), а затем, координаты точек

Расстояние между точками
К₁ и L₁; равно

Ответ:

Задание
87.

В равнобочной трапеции PQRS
(QR || PS) известны длины сторон QR = 1, PS = 4. Точки Р₁, Q₁,
R₁ и S₁ лежат по одну сторону от плоскости трапеции, причем
прямые PP₁, QQ₁, RR₁, SS₁ перпендикулярны
этой плоскости и РР₁ = 1, QQ₁ = 7, RR₁ = 2,
SS₁ = 1. Точки К₁ и L₁ лежат на отрезках P₁R₁
и Q₁S₁ соответственно. Найдите длину отрезка К₁L₁,
если Р₁K₁ : К₁P₁ = 3 : 2, Q₁L₁
: L₁S₁ = 2 : 3.

Ответ:

Задание
88.

В равнобочной трапеции ABCD
(AD || BC) известны длины сторон AD = 10; ВС = 2. Точки А₁, B₁,
С₁ и D₁ лежат по одну сторону от плоскости трапеции, причем
прямые ААг, BBlt ССг и DD: перпендикулярны этой плоскости, AA₁ =
1, ВВ₁ = 2, СС₁ = 2, DD₁ = 4. Точки М₁
и N₁ лежат на отрезках А₁С₁ и B₁D₁
соответственно. Найдите длину отрезка М₁N₁, если А₁М₁
: М₁С₁ = 2 : 1, B₁N₁ : N₁D₁
= 1 : 2.

Решение.

Пусть начало координат совпадает
с точкой А, отрезок АС лежит на оси Ах, ось Ау лежит в плоскости ABC и перпендикулярна
оси Аx; точки А₁ лежит на оси Az (рис.).

Обозначив сторону АВ основания
призмы через а и учитывая, что высота АА₁ = 2, найдем координаты
точек

Далее имеем

Косинус угла между прямыми
АС₁ и А₁В равен модулю косинуса угла между векторами

откуда

Раскрывая модуль, получаем

Ответ:

Задание 89.

В правильной треугольной
призме АВСА₁В₁С₁ (АА₁ || В₁
|| СС₁) угол между прямыми АС₁ и А₁В равен

АА₁ = 2. Найдите
АВ₁.

Решение.

Расположим оси координат
так, как показано на рис.

Имеем

Поскольку вектор

точка Р имеет координаты

Пусть х, у и z — координаты
точки М. По условию

откуда

уравнение сферы с центром в точке С и радиусом

Так как куб вырезает из
сферы

Ответ:

Задание
90.

Дан куб ABCDA₁B₁C₁D₁
(АА₁ II ВВ₁ II СС₁ II DD₁) с ребром
а. На диагонали А₁:С взята точка Р так, что А₁Р : A₁C
= 8 : 9. Внутри куба находится поверхность S, состоящая из точек М, для которых
А₁М : РМ = 3. Найдите площадь поверхности S.

Ответ:

Задание
91.

Дан куб ADCDA₁B₁C₁D₁
(AA₁ || ВВ₁ II СС₁ II DD₁) с ребром
а. Точки N и Р — середины ребер А₁В₁ и CD соответственно.
На отрезке NP взята точка Q так, что NQ : NP = 2:3. Внутри куба находится тело
G, состоящее из точек М, для которых

Найдите объем тела G.

Решение.

Введем систему координат
(рис.)

так, чтобы начало координат
совпало с вершиной A, ось Ох была направлена вдоль ребра (AD), Оу — вдоль ребра
(АВ), а Оz — вдоль ребра (AA₁). Тогда

— середина ребра

середина ребра (C₁D₁).
Пусть центр сферы имеет координаты (х; у; z). Обозначив искомый радиус через
R, имеем

откуда, вычитая из второго равенства первое, получаем

Подставляя

во второе и третье равенства
и вычитая извторого равенства третье, получим

Теперь, подставляя

в первое и третье уравнения,
находим

Таким образом,

Ответ:

Задание
92.

Ребро куба имеет длину а.
Найдите радиус сферы, проходящей через точки A, D и середины ребер В₁С₁
и C₁D₁.

Ответ:

Задание
93.

Дан куб ABCDA₁B₁C₁D₁,
длина ребра которого равна а. Найдите радиус сферы, проходящей через точки А,
В₁, Е и F, если точки Е и F лежат на ребре СС₁ и СЕ =
EF = FC₁.

Решение.

Расположим систему координат
Oxyz так, чтобы ее начало совпало с вершиной А, а координатные плоскости совпали
с гранями куба (рис.).

Так как радиус сферы, проведенный
в точку касания, перпендикулярен касательной плоскости, то из условия следует,
что

— центр первой сферы радиуса

— центр второй сферы радиуса
|1 – z|. Точка касания сфер лежит на прямой, проходящей через их
центры, поэтому длина вектора

должна быть равна сумме радиусов этих сфер. Получаем уравнение

откуда

Значит,

— радиусы сфер,

Пусть М – точка касания
сфер. Тогда

а координаты точки М получаем, прибавляя к координатам точки

координаты вектора

Следовательно,

Ответ:

Задание
94.

Длина ребра куба ABCDA₁B₁C₁D₁
равна 1. Одна сфера радиуса

касается плоскости ABC в
точке А, другая сфера касается плоскости А₁B₁С₁
в точке E₁ лежащей на отрезке В₁С₁, причем
В₁Е₁ : Е₁С₁ = 2 :1. Известно, что
сферы касаются друг друга внешним образом и точка их касания лежит внутри куба.
Найдите расстояние от точки касания сфер до точки D.

Ответ:

Задание
95.

Длина ребра куба ABCDA₁B₁C₁D₁
равна 1. Одна сфера радиуса

касается плоскости ABC
в точке В, другая сфера касается плоскости А₁В₁С₁
в точке Е₁, лежащей на отрезке С₁D₁ ,причем
С₁Е₁ : Е₁D₁ = 1 :2 . Известно, что
эти сферы касаются друг друга внешним образом и точка их касания лежит внутри
куба. Найдите расстояние от точки касания сфер до точки С.

Решение.

Совместим начало координат
с центром шара так, чтобы координатные оси были параллельны заданным: Ох ||
(AA₁), Оy II (ВВ₁), Оz II (СС₁).

Пусть х₀, у₀, z₀ — координаты точки М. Так
как уравнение сферы имеет вид х² + у² + z²
= 121, то |ОМ| = х₀² + y₀² + z₀²
=59.

Запишем уравнения прямой
(СС₁): х = х₀, у = y₀, z = z₀ и
найдем координаты z_c точек С и С₁ пересечения этой прямой
со сферой.

Имеем 121 = х₀²
+ y₀² + z₀² т.е.

так как

х₀²
+ y₀² + z₀² = 59 – z₀²

Решив последнее уравнение,
получаем

Аналогично, записав уравнения
прямой (BB₁): х = х₀, у = у₀, z = z₀,
находим координаты

Длина отрезка

откуда следует, что у₀² = 19. Наконец, точно так же получаем,
что длина отрезка

Ответ:

20 см.

Задание
96.

На сфере радиуса 11 см взяты
точки А, А₁, В, B₁ С и С₁, что прямые АА₁,
ВВ₁ и СС₁ взаимно перпендикулярны и пересекаются в точке
М, отстоящей от центра сферы на расстоянии

Найдите длину отрезка АА₁,
если известно, что длина отрезка BB₁ равна 18 см, а точка М делит
отрезок СС₁ в отношении

Ответ:

Задание
97.

Отрезки АА₁,
ВВ₁, СС₁, концы которых лежат на сфере радиуса 10 см,
попарно перпендикулярны и пересекаются в точке М. Длина отрезка АА₁
равна 12 см, длина отрезка ВВ₁ равна 18 см. Найдите расстояние от
центра сферы до точки М, если известно, что отношение длины отрезка СМ к длине
отрезка МС₁ равно 11:3.

Решение.

Расположим систему координат
Охуz так, чтобы координатная плоскость Оху содержала грань ABCD куба, ребра
(АВ) II Оу, (AD) II Ох, а ось Оz прошла через центр квадрата ABCD (рис.).

Запишем уравнения:

Далее запишем координаты
точек

Обозначим через М и N точки
пересечения прямой (EF) со сферой

считая от точки E. Тогда
координаты точки М получаем из координат точки Е прибавлением координат вектора

a координаты точки N —
прибавлением координат вектора

Подсчет дает:

Точки

Подстановка их координат
в уравнение сферы приводит к системе

а нужно найти

Решив систему, находим

Ответ:

Задание
98.

Ребро куба ABCDA₁B₁C₁D₁
равно а. На диагоналях АС и B₁D₁ граней куба взяты соответственно
точки Е и F так, что вписанная в куб сфера делит отрезок EF на три части, отношение
длин которых равно 3:7:2, считая от точки Е. Найдите длину EF.

Решение.

Расположим систему координат
Oxyz так, чтобы начало координат совпало с вершиной К; имеет N(1; 0; 0), L(0;
1; 0), К₁ (0;0; 1).Тогда

– центр куба. Уравнение
плоскости, проходящей через точки А, В и С, имеет вид

Подставляя в это равенство
координаты точек

получим уравнение плоскости:
9х – 8у – 5z + 2 = 0. Вектор n = {9; -8; -5} является направляющим вектором
прямой, проходящей через К₁ (0; 0; 1) перпендикулярно указанной плоскости.
Пусть Р — точка пересечения этой прямой и плоскости. Запишем уравнения

Подставляем эти выражения в уравнение 9x – 8у – 5г + 5 + 2 = 0 и находим точку

остается наити

Так как

Ответ:

Задание
99.

Длина ребра куба KLMNK₁L₁M₁N₁
равна 1. На ребре KL взята точка А так, что длина отрезка КА равна

а на ребре ММ₁
— точка В так, что длина отрезка М₁В равна 2/5. Через центр куба
и точки А и В проведена плоскость, точка Р — проекция точки К₁ на
эту плоскость. Найдите длину отрезка АР.

Решение.

Введем систему координат
Oxyz так, чтобы вершина А совпала с началом координат, ребро AD лежало на оси
абсцисс, ребро АВ — на оси ординат, а ребро АА₁ — на оси аппликат.
Тогда: D (а; 0; 0),

По условию отрезки MN и
PQ ортогональны и пересекаются. Первое условие означает, что

откуда получаем, что у =
2х – а. Второе условие влечет компланарность векторов

Значит, нужно найти числа

откуда

Решив эту систему, получим

Теперь найдем

а тогда искомая длина

Ответ:

Задание
100.

Длина ребра куба ABCDA₁B₁C₁D₁
равна а. Точки Р, К, L — середины ребер AA₁,A₁D₁
и В₁С₁ соответственно, точка Q — центр грани CC₁D₁D.
Отрезок MN, концы PQ и перпендикулярен ей. Найдите длину этого отрезка.

Указание.

См. аналогичную задачу 98.

Ответ:

Задание
101.

Длина ребра куба ABCDA₁B₁C₁D₁
равна 1. На ребре АА₁ взята точка Е так, что АЕ =

а на ребре ВС – точка F
так, что BF =

Через центр куба и точки
Е и F проведена плоскость. Найдите расстояние от вершины В₁до этой
плоскости.

Указание.

Запишите уравнения прямой
АК и плоскости, проходящей через точку N перпендикулярно прямой АК. Расстояние
от точки N до точки пересечения указанных прямой и плоскости и является искомым.

Ответ:

Задание
102.

В кубе ABCDA₁B₁C₁D₁,
ребро которого равно 6, точки М и N — середины реберАВ и В₁С₁
соответственно, а точка К расположена на ребре DC так, что DK = 2КС. Найдите
расстояние от точки ./V до прямой АК.

Указание.

Покажите, что плоскость,
проходящая через точки В, B₁ и D, параллельна отрезку AA₁
и найдите расстояние от точки А до этой плоскости.

Ответ:

Задание
103.

Дан куб ABCDA₁B₁C₁D₁
с ребром а. Найдите расстояние от ребра АА₁ до диагонали B₁D.

Решение.

Выберем систему координат
Oxyz так, чтобы вершина Р совпала с началом координат, ось Оz была направлена
вдоль ребра PP₁, а точка Q лежала в верхней полуплоскости координатной
плоскости Оху (рис.).

Тогда:

и, значит,

Проекцию отрезка АВ

на прямую RP₁
(или на

найдем по формуле

откуда

Ответ:

Задание
104.

В прямой треугольной призме
PQRP₁Q₁R₁ (PP₁ II QQ₁
II RR₁) на ребрах PQ и P₁R₁ взяты соответственно
точки А и В так, что РА : AQ = 1 : 3 и Р₁В : BR₁ = 3:4.
Угол QRP равен 30°. Отрезок EF является проекцией отрезка АВ на прямую RP₁.V
Найдите длину отрезка EF, если известно, что высота призмы равна 13 см, PQ =
8 см, PR = 14 см.

Ответ:

Задание
105.

В основании прямой треугольной
призмы KMNK₁M₁N₁ (KK₁ || ММ₁
II NN₁) лежит треугольник KMN, угол MKN равен 45°. На ребрах КМ и
К₁R выбраны соответственно точки Q и R так, что KQ : QM = = 1 : 4
и K^R : RN± =4:5. Отрезок CD является проекцией отрезка NK₁ на прямую
QR. Найдите длину отрезка CD, если известно, что КК₁ = 8 см, KQ =
1 см; KN = 9 см.

Указание.

См. решение задачи 106.

Ответ:

Задание
106.

Каждое из ребер треугольной
пирамиды ABCD имеет длину 1. Точка Р на ребре АВ, точка Q на ребре
ВС и точка R на ребре CD взяты так, что

и CR =

Плоскость PQR пересекает
прямую AD в точке S. Найдите величину угла между прямыми SP и SQ.

Решение.

Введем систему координат
Охуz, поместив начало координат в середину ребра АВ так, чтобы ось Оу прошла
через вершину С, а сторона АВ лежала на оси Ох (рис.).

Данная пирамида — правильный
тетраэдр. Определяем координаты нужных точек и векторов:

Далее находим вектор

перпендикулярный векторам

Из системы равенств

получим

Тогда уравнение плоскости,
проходящей через точки

Далее, из равенства

следует, что

Перейдем к отысканию значения
t, при котором точка Н принадлежит указанной плоскости. Hi плоскости, получаем

Теперь запишем координаты
точки

и векторов

Складывая эти величины, находим периметр треугольника HEG.

Ответ:

Задание
107.

Каждое из ребер прямоугольной
пирамиды ABCD имеет длину 1. Точка Е на ребре АВ, точка F на ребре ЕС и точка
G на ребре CD взяты так, что

Плоскость EFG пересекает
прямую AD в точке Н. Найдите периметр тр. HEG.

Указание.

Основание конуса лежит в
плоскости у = 2.

Ответ:

Задание
108.

Точки А(1; 2; -1), В(-2;
-2; -1) и С(-2; 2; 3) лежат на окружности основания конуса, а точка

на его боковой поверхности.
Найдите площадь полной поверхности конуса.

Ответ:

Задание
109.

Точки А(1; 2; -2), (4; 2;
-2) и С(3; 4; -2) лежат на окружности основания конуса, высота которого равна
3. Найдите координаты его вершины, если конус пересекает плоскость z = 0.

Решение.

а) Положим |АВ| = 2а, а
> 0. Введем на плоскости систему координат Оху так, что А(-а; 0), В(0; а),
а ось ординат проходит через середину отрезка АВ перпендикулярно этому отрезку
(рис.).

Пусть М(х; у) — произвольная
точка, принадлежащая искомому множеству.

Согласно условию координаты
точки М(х; у) должны удовлетворять равенству

т.е. (х + а)²
+ у² = k²[(x – a)² + у²],

откуда (k² –
1)x² – 2(k² + 1)ax + (k² – 1)y²
+ (k² – 1)a² = 0.

Если k = 1, то это прямая
х = 0. Если же k # 1, то это семейство окружностей

В частности, при

получаем (х – 2а)²
+ у² = За², где

Ответ:

a) при k = 1 — прямая;
при k # 1 — окружности

б) Прямые. В указанной системе координат их уравнение

в) При

— пустое множество; при

— точка; при

— окружности, имеющие в
указанной системе координат уравнения

• Задачи на отыскание геометрических мест точек, удовлетворяющих каким-либо
требованиям, часто решаются достаточно просто, если ввести подходящим образом
координатную систему. То же относится и к некоторым задачам на доказательство.

Задание
110.

На плоскости даны точки
А и Б. Найдите множество всех точек М плоскости, для которых выполнено условие:

Указание.

Введите систему координат
так, чтобы данная прямая совпала с осью абсцисс, а данная точка лежала на оси
ординат и имела координаты (0; а), где а > 0 — расстояние от данной точки
до прямой. В этом случае уравнения искомых кривых имеют вид 2ау = х²
+ а².

Ответ:

Парабола.

Задание
111.

На плоскости даны прямая
и не лежащая на ней точка. Найдите множество точек, равноудаленных от этой прямой
и этой точки.

Указание.

Введите систему координат,
у которой оси совпадают с заданными прямыми. В этой системе искомые геометрические
места точек определяются уравнениями:

Задание
112.

На плоскости даны две взаимно
перпендикулярные прямые. Найдите множество всех точек М плоскости, для которых:

а) произведение расстояний
до данных прямых равно модулю разности этих расстояний;
б) модуль разности расстояний до данных прямых равен модулю разности величин,
обратных этим расстояниям;
в) сумма расстояний до данных прямых равна сумме величин, обратных этим расстояниям.

Ответ:

Окружность с центром в точке
С и радиусом R = |АС|.

Задание
113.

Точка С лежит на отрезке
АВ так, что АС : СВ = = 2 :1. Найдите множество точек М плоскости, для которых
< MCE = 2< MAC.

Решение.

Введем систему координат
Охуz так, чтобы точка А совпадала с ее началом, точка В лежала на оси абсцисс,
а точка С принадлежала плоскости Охуz. Тогда А(0; 0; 0), B(x₁; 0;
0), С(х₂; у₂; 0), D(x₃; у₃; z₃).

Найдем координаты нужных
векторов:

По условию

Теперь получим

Задание
114.

В пространстве даны точки
А, В, С и D, причем

Докажите, что

Решение.

Введем систему координат
Oxyz так, чтобы А = 0, точка В лежала на оси Ох, а отрезок CD был параллелен
координатной плоскости Оху. Тогда: А(0; 0; 0), B(x₁; 0; 0), С(х₂;
у₂; z), D(x₃; у₃; z),

Запишем следующие векторы:

Отсюда видно, что

Теперь требуемое неравенство
следует из общего неравенства:

Задание
115.

В пространстве даны два
отрезка АВ и CD, не лежащие в одной плоскости. Пусть MN — отрезок, соединяющий
их середины. Докажите, что |АС| + |BD| > 2|MN|.

Ответ:

Сфера

Задание
116.

Найдите множество точек
пространства, сумма квадратов расстояний которых до двух данных точек А(2; 3;
-1) и В(1; – 1; 3) равна 21.

Поделитесь этой записью или добавьте в закладки