Как найти длину, если известен объем
Если известен объем трехмерной геометрической фигуры, в большинстве случаев можно найти некоторые ее линейные размеры. Главный линейный размер любой фигуры – это длины ее сторон, а для сферы – радиус. Для различных типов фигур он находится по-разному.

Вам понадобится
- Объемы измеряемых фигур, свойства многогранников
Инструкция
Зная объем правильного многогранника (выпуклого многогранника, стороны которого правильные многоугольники) можно вычислить его сторону. Чтобы найти длину стороны тетраэдра (правильного четырехгранника, грани которого являются равносторонними треугольниками), умножьте его объем на 12 и разделите результат на корень квадратный из 2. Из полученного числа извлеките кубический корень.
Чтобы найти сторону куба, который является шестигранником, каждая грань которого квадрат, из его объема извлеките кубический корень. Вычислите сторону октаэдра, который состоит из 8 треугольных граней, каждая из которых является правильным треугольником, умножив его объем на 3 и поделив на корень квадратный из 2. Из полученного числа извлеките кубический корень. Найдите сторону додекаэдра, многогранника состоящего из 12 правильных пятиугольников, для чего поделите его объем на число 7,66, и извлеките из результата кубический корень.
Чтобы найти радиус шара, объем которого известен, умножьте этот объем на 3 и поделите последовательно на числа 4 и 3,14. Их полученного результат извлеките кубический корень.
Если же фигура не является правильным многогранником, то, зная ее объем, можно вычислить длины только некоторых ее элементов. Зная объем и площадь основания призмы, можно найти ее высоту. Для этого поделите значение объема на площадь основания h=V/S. Чтобы найти другие линейные элементы, нужно знать параметры площади основания, например, если это квадрат, из значения площади извлеките корень квадратный, это и будет сторона основания.
Если известен объем цилиндра, то можно найти его высоту, зная радиус. Для этого объем последовательно поделите на число 3,14 и квадрат радиуса основания. Если же известна высота, то найдите радиус основания, поделив объем на число 3,14 и значение высоты, а из результата извлеките корень квадратный.
Чтобы найти высоту пирамиды через объем, поделите его на площадь основания, а результат умножьте на число 3.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти длины сторон прямоугольного параллелепипеда зная его объем и соотношение сторон
Екатерина Шигаева
Знаток
(267),
на голосовании
9 лет назад
Как найти длины сторон прямоугольного параллелепипеда зная его объем и соотношение сторон
Пример:
Объем = 5000 см^3
Стороны:
a=x
b=x*1,618
c=x*2,618
Голосование за лучший ответ
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
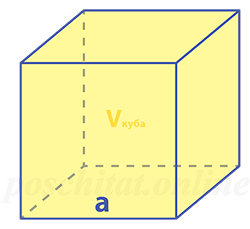
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
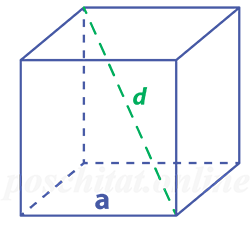
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
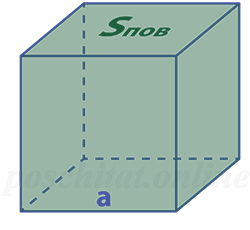
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также
Найдите правильный ответ на вопрос ✅ «Как найти сторону параллелепипеда, если известен объем (44 куб. м) и две стороны? Стороны: в=8 м, с=2 м. Помогите!)) …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » Математика » Как найти сторону параллелепипеда, если известен объем (44 куб. м) и две стороны? Стороны: в=8 м, с=2 м. Помогите!))
Ребро куба
Стороны фигур
Куб — это четырехугольная призма, все шесть граней которой являются квадратами.
Калькулятор расчета длины ребра куба через объем
Длины трех ребер куба (длина, ширина, высота) имеют равные измерения. Объем куба равен длине ребра, возведенной в третью степень.
V = a3 ,
где Y — объем куба, а — ребро куба.
Если известен объем куба V, длину ребра (а) рассчитываем по формуле:
Калькулятор расчета длины ребра куба через диагональ
Проведенный внутри куба отрезок, соединивший вершины, расположенные на противоположных сторонах, является диагональю куба. Соединив диагональ и боковое ребро, исходящее из вершины диагонали через диагональ основания, получим прямоугольный треугольник. Его гипотенузой будет диагональ куба, а катетами — боковое ребро и диагональ основания. Через теорему Пифагора находим диагональ куба:
d = a√3 ,
где а — ребро куба, d — диагональ куба.
Если известна диагональ куба, его ребро определяем как отношение диагонали к корню из 3 по формуле:
a = d/√3 ,