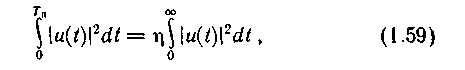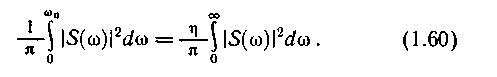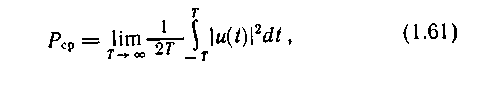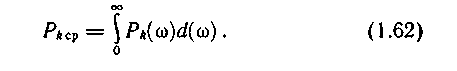Как найти длительность импульса по спектру - Сайт, где вы сможете решить свои вопросы

Анализируя
спектр одиночного прямоугольного
импульса (см. рис. 1.10), можно установить,
что при увеличении его длительности τ
от 0 до
спектр сокращается от безграничного
(у дельта-функции) до одной спектральной
линии в начале координат, соответствующей
постоянному значению сигнала. Это
свойство сокращения ширины спектра
сигнала при увеличении его длительности
и наоборот справедливо для сигналов
любой формы. Оно вытекает непосредственно
из особенностей прямого и обратного
интегрального преобразования Фурье, у
которых показатель степени экспоненциальной
функции в подынтегральных выражениях
имеет переменныеt
и ω
в виде
произведения.

Рассмотрим
функцию u(t)
определенной
продолжительности и функцию u(t),длительность
которой при λ>1
будет в λ
раз меньше. Считая, что u(t)
имеет
спектральную характеристику S(jω),
найдем соответствующую характеристику
S(jω)
для u(t):

где

=λt.

Следовательно,
спектр укороченного в λ
раз сигнала
ровно в λ
раз шире.
Коэффициент l/λ
перед
S(jω/λ)
изменяет
только амплитуду гармонических
составляющих и на ширину спектра не
влияет.

Другой важный
вывод, также являющийся прямым следствием
Фурье-преобразования, заключается в
том, что длительность сигнала и ширина
его спектра не могут быть одновременно
ограничены конечными интервалами: если
длительность сигнала ограничена, то
спектр его неограничен, и, наоборот,
сигнал с ограниченным спектром длится
бесконечно долго. Справедливо соотношение

где
Δt
— длительность
импульса; Δf
— ширина
спектра импульса; С — постоянная
величина, зависящая от формы импульса
(при ориентировочных оценках обычно
принимают С=1).

Реальные сигналы
ограничены во времени, генерируются и
передаются устройствами, содержащими
инерционные элементы (например, емкости
и индуктивности в электрических цепях),
и поэтому не могут содержать гармонические
составляющие сколь угодно высоких
частот.

В
связи с этим возникает необходимость
ввести в рассмотрение модели сигналов,
обладающие как конечной длительностью,
так и ограниченным спектром. При этом
в соответствии с каким-либо критерием
дополнительно ограничивается либо
ширина спектра, либо длительность
сигнала, либо оба параметра одновременно.
В качестве такого критерия используется
энергетический критерий, согласно
которому практическую длительность Т_п
и практическую ширину спектра _п
выбирают так, чтобы в них была сосредоточена
подавляющая часть энергии сигнала.

Для
сигналов, начинающихся в момент времени
t₀
= О,
практическая длительность определяется
из соотношения

где
η —
коэффициент, достаточно близкий к 1 (от
0,9 до 0,99 в зависимости от требований к
качеству воспроизведения сигнала).

Принимая
во внимание равенство Парсеваля (1.56),
для практической ширины спектра сигнала
соответственно имеем

§ 1.6. Спектральная плотность мощности детерминированного сигнала

Величина
,
характеризующая распределение энергии
по спектру сигнала и называемая
энергетической спектральной плотностью,
существует лишь для сигналов, У которых
энергия за бесконечный интервал времени
конечна и, следовательно, к ним применимо
преобразование Фурье.

Для
незатухающих во времени сигналов энергия
бесконечно велика и интеграл (1.54)
расходится. Задание спектра амплитуд
невозможно. Однако средняя мощность
Р_ср,
определяемая соотношением

оказывается
конечной. Поэтому применяется более
широкое понятие «спектральная плотность
мощности». Определим ее как производную
средней мощности сигнала по частоте и
обозначим Ρ_k(ω):

Индексом
k
подчеркивается,
что здесь мы рассматриваем спектральную
плотность мощности как характеристику
детерминированной функции u(t),
описывающей реализацию сигнала.

Эта характеристика
сигнала менее содержательна, чем
спектральная плотность амплитуд, так
как лишена фазовой информации [см.
(1.38)]. Поэтому однозначно восстановить
по ней исходную реализацию сигнала
невозможно. Однако отсутствие фазовой
информации позволяет применить это
понятие к сигналам, у которых фаза не
определена.

Для
установления связи между спектральной
плотностью Ρ_k(ω)
и спектром
амплитуд воспользуемся сигналом u(t),
существующим
на ограниченном интервале времени
(—T<.t<T).
К такому
сигналу применимо равенство Парсеваля
(1.56). Из сравнения (1.62) с правой частью
соотношения (1.56) следует

где
— спектральная плотность мощности
сигнала, ограниченного во времени.

В дальнейшем будет
показано (см. § 1.11), что, усредняя эту
характеристику по множеству реализаций,
можно получить спектральную плотность
мощности для большого класса случайных
процессов.

Соседние файлы в предмете Информационные технологии

Источник

Спектр периодической последовательности прямоугольных импульсов

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Вводные замечания

В предыдущих разделах мы рассмотрели

разложение периодических сигналов в ряд Фурье,

а также изучили

некоторые свойства
представления периодических сигналов рядом Фурье.

Мы говорили, что периодические сигналы можно представить как ряд комплексных экспонент,
отстоящих друг от друга на частоту $Delta omega = frac{2pi}{T}$ рад/c,
где — период повторения сигнала.
В результате мы можем трактовать представление сигнала в виде ряда комплексных гармоник как комплексный спектр сигнала.
Комплексный спектр, в свою очередь, может быть разделен на амплитудный и фазовый спектры периодического сигнала.

В данном разделе мы рассмотрим спектр периодической последовательности прямоугольных импульсов,
как одного из важнейших сигналов, используемого в практических приложениях.

Спектр периодической последовательности прямоугольных импульсов

Пусть входной сигнал s(t) представляет собой периодическую последовательность
прямоугольных импульсов амплитуды , длительности tau секунд следующих с
периодом секунд, как это показано на рисунке 1

Рисунок 1. Периодическая последовательность прямоугольных импульсов

Единица измерения амплитуды сигнала зависит от
физического процесса, который описывает сигнал s(t) .
Это может быть напряжение, или, сила тока,
или любая другая физическая величина со своей единицей измерения,
которая меняется во времени как s(t) .
При этом, единицы измерения амплитуд спектра
, $omega_n = frac{2 pi}{T} n$ ,
будут совпадать с единицами
измерения амплитуды исходного сигнала.

Тогда спектр , $omega_n = frac{2 pi}{T} n$ ,
данного сигнала может быть представлен как:

(1)

Спектр периодической последовательности прямоугольных импульсов представляет собой множество гармоник с огибающей вида
$S(omega) = A , frac{sin left(omega tau/2 right) }{omega T/2}$ .

Свойства спектра периодической последовательности прямоугольных импульсов

Рассмотрим некоторые свойства огибающей спектра периодической последовательности прямоугольных импульсов.

Постоянная составляющая огибающей S(0) может быть получена как предел:

(2)

Для раскрытия неопределенности воспользуемся правилом Лопиталя [1, стр. 257]:

(3)

где $Q = frac{T}{tau} > 1$ называется скважностью импульсов и задает отношение
периода повторения импульсов к длительности одиночного импульса.

Таким образом, значение огибающей на нулевой частоте равно амплитуде импульса деленной на скважность.
При увеличении скважности (т.е. при уменьшении длительности импульса при
фиксированном периоде повторения) значение огибающей на нулевой частоте уменьшается.

Используя скважность импульсов выражение (1) можно переписать в виде:

(4)

где .

Нули огибающей спектра последовательности прямоугольных импульсов можно получить из уравнения:

(5)

Знаменатель обращается в ноль только при , однако, как мы выяснили выше
$S(0) = frac{A}{Q} neq 0$ , тогда решением уравнения будет

(6)

Тогда огибающая обращается в ноль если

(7)

На рисунке 2 показана огибающая спектра периодической последовательности
прямоугольных импульсов (пунктирная линия) и частотные
соотношения огибающей и дискретного спектра .

Рисунок 2. Cпектр периодической последовательности
прямоугольных импульсов

Также показаны амплитудная огибающая , амплитудный спектр , а также фазовая огибающая и фазовый спектр
.

Из рисунка 2 можно заметить, что фазовый спектр принимает значения pm pi
когда огибающая имеет отрицательные значения.
Заметим, что и соответствуют одной и
той же точке комплексной плоскости равной .

Пример спектра периодической последовательности прямоугольных импульсов

Пусть входной сигнал s(t) представляет собой периодическую последовательность
прямоугольных импульсов амплитуды A = 2 , следующих с периодом T = 4 секунды
и различной скважностью .
На рисунке 3а показаны временные осциллограммы указанных сигналов,
их амплитудные спектры (рисунок 3б),
а также непрерывные огибающие спектров (пунктирная линия).

Рисунок 3. Cпектр периодической последовательности
прямоугольных импульсов при различном значении скважности
а — временные осциллограммы; б — амплитудный спектр

Как можно видеть из рисунка 3, при увеличении скважности сигнала, длительность импульсов s(t) уменьшается,
огибающая спектра расширяется и уменьшается по амплитуде (пунктирная линия).
В результате, в пределах главного лепестка увеличивается количество гармоник спектра .

Спектр смещенной во времени периодической последовательности прямоугольных импульсов

Выше мы подробно изучили спектр периодической последовательности прямоугольных
импульсов для случая, когда исходный сигнал s(t) являлся симметричным относительно t = 0 .
В результате спектр такого сигнала является вещественным и задается выражением (1).
Теперь мы рассмотрим, что произойдет со спектром сигнала $s_{textrm{sh}}(t)$
если мы сместим сигнал s(t) во времени,как это показано на рисунке 4 .

Рисунок 4. Сдвинутая во времени периодическая последовательность прямоугольных импульсов

Смещенный сигнал $s_{textrm{sh}}(t)$ можно представить как сигнал s(t) ,
задержанный на половину длительности импульса
$s_{textrm{sh}}(t) = s left( t - frac{tau}{2}right)$ .
Спектр $S_{textrm{sh}}(omega_n)$ смещенного сигнала $s_{textrm{sh}}(t)$ можно представить
согласно свойству

циклического временного сдвига

как:

(8)

Таким образом, спектр периодической последовательности прямоугольных импульсов, смещенной относительно нуля, не
является чисто вещественной функцией, а приобретает дополнительный фазовый множитель
$expleft( -j omega_n frac{tau}{2}right)$ .
Амплитудный $left|S_{textrm{sh}}(omega_n) right|$ и фазовый $Phi_{textrm{sh}}(omega)$
спектры показаны на рисунке 5.

Рисунок 5. Амплитудный и фазовый спектры сдвинутой во времени периодической
последовательности прямоугольных импульсов

Из рисунка 5 следует, что сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала,
но добавляет линейную составляющую к фазовому спектру сигнала.

Выводы

В данном разделе мы получили аналитическое выражение для спектра периодической последовательности прямоугольных импульсов.

Мы рассмотрели свойства огибающей спектра периодической последовательности прямоугольных импульсов и привели примеры
спектров при различном значении скважности.

Также был рассмотрен спектр при смещении во времени последовательности прямоугольных импульсов и показано,
что смещение во времени изменяет фазовый спектр и не влияет на амплитудный спектр сигнала.

Программная реализация в библиотеке DSPL

Данные для построения рисунков данного раздела были просчитаны при использовании

библиотеки DSPL-2.0

Ниже приведён исходный код программы расчета данных для построения рисунка 3:

fourier_series_pimp_q.c


#include <stdio.h>
#include <string.h>
#include "dspl.h"

/* Размер векторов входных сигналов и огибающей спетра */
#define N  1000 

/* Период повторения импульса. Для изменения скважности мы будем менять 
 * длительность импульса при фиксированном периоде повторения */
#define T  4.0

/* Амплитуда */
#define A  2.0

/* Количество спектральных гармоник разложения в ряд Фурье  */
#define M  41


/* длина команды Gnuplot */
#define PLOTCMD_LEN 256


int main(int argc, char* argv[])
{

  double    t1[N];   /* время (сек) на одном периоде повторения      */
  double    t4[N];   /* время (сек) на четырех периодах повторения   */
  double    s[N];    /* входной сигнал                               */
  complex_t S[M];    /* комплексный спектр периодического сигнала    */
  double    Smag[M]; /* амплитудный спектр периодического сигнала    */
  double    w[M];    /* частота (рад/c) дискретного спектра          */
  double    wc[N];   /* частота (рад/с) огибающей спектра            */
  double    Sc[N];   /* огибающая спектра                            */
  double    tau;     /* длительность импульса                        */

  /* скважность */
  double    Q[3] = {5.0, 2.0, 1.25};

  int q, m, n;
  
  char fname[64];            /* имя файла данных */
  char plotcmd[PLOTCMD_LEN]; /* Команда Gnuplot  */ 
  
  void* hdspl;  /* DSPL handle        */
  void* hplot;  /* GNUPLOT handle     */
  
  hdspl = dspl_load();
  if(!hdspl)
  {
    printf("Cannot to load libdspl!n");
    return 0;
  }
  
  /* Вектор частот непрерывной огибаюхей вида sin(w/2*tau) / (w/2*T) */
  linspace(-M_PI*(double)M/(double)T, M_PI*(double)M/(double)T,  N, DSPL_SYMMETRIC, wc);
  
  /* заполнение массива временных отсчетов  */
  /* на одном периоде повторения сигнала    */
  linspace(-T/2.0, T/2.0,  N, DSPL_PERIODIC, t1);
  
  /* заполнение массива временных отсчетов
   * на 4-x периодах повторения сигнала
   * для отображения на осциллограмме */
  linspace(-T*2.0, T*2.0,  N, DSPL_PERIODIC, t4);
  
  
  /* Построение графиков пакетом GNUPLOT */
  gnuplot_create(argc, argv, 800, 640,  "img/fourier_series_rec.png", &hplot);
  gnuplot_cmd(hplot, "unset key");
  gnuplot_cmd(hplot, "set multiplot layout 3,2 rowsfirst");
  gnuplot_cmd(hplot, "set yrange [0:2.2]");
  
  for(q = 0; q < 3; q++)
  {
    tau = T/Q[q];

    /* 4 периода повторения п-импульса скважности Q[q] */
    signal_pimp(t4, N, A, tau, 0.0, T, s);

    /* сохранение в текстовый файл временных осциллограмм */
    sprintf(fname, "dat/pimp_time_%.2lf.csv", Q[q]);
    writetxt(t4, s, N, fname);

    /* Построение временнОй осциллограммы */
    sprintf(plotcmd, "plot '%s' with lines", fname);
    gnuplot_cmd(hplot, plotcmd);

    /* один период повторения п-импульса скважности Q[q] */
    signal_pimp(t1, N, A, tau, 0.0, T, s);

    /* разложение в ряд Фурье */
    fourier_series_dec(t1, s, N, T, M, w, S);

    /* Рассчет амплитудного спектра */
    for(m = 0; m < M; m++)
    {
      /*printf("S[%d] = %f     %fn", m, RE(S[m]), IM(S[m]));*/
      Smag[m] = ABS(S[m]);
    }

    /* Сохранение в файл амплитудного спетра для скважности Q[q] */
    sprintf(fname, "dat/pimp_freq_discrete_%.2lf.csv", Q[q]);
    writetxt(w, Smag, M, fname);

    /* Построение на график амплитудного спектра для заданной скважности */
    sprintf(plotcmd, "plot '%s' with  impulses lt 1 ,\", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);

    sprintf(plotcmd, "'%s'  with points pt 7 ps 0.5 lt 1 ,\", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);

    /* Расчет огибающей */
    for(n = 0; n < N; n++)
      Sc[n] = (wc[n] == 0.0) ? A/Q[q] : fabs( A * sin(0.5*wc[n]*tau) / (0.5*wc[n] * T));

    /* сохранение огибающей в файл для скважности Q[q] */
    sprintf(fname, "dat/pimp_freq_cont_%.2lf.csv", Q[q]);
    writetxt(wc, Sc, N, fname);
    
    /* Построение на график непрерывной огибающей 
    амплитудного спектра для заданной скважности */
    sprintf(plotcmd, "'%s'  with lines", fname);
    printf("%sn", plotcmd);
    gnuplot_cmd(hplot, plotcmd);
  }

  gnuplot_cmd(hplot, "unset multiplot");
  gnuplot_close(hplot);
  
  /* remember to free the resource */
  dspl_free(hdspl);
  return 0;
}

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Преобразование Фурье непериодических сигналов
Свойства преобразования Фурье

Список литературы

[1]

Основы математического анализа.
Москва, Наука, 1965, 572 c.

[2]

Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[4]

Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.

[5]

Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:36)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

В соответствии со спектральным способом анализа прохождения сигналов через линейные цепи любой случайный сигнал S(T) можно представить в виде бесконечной суммы элементарных аналитически однотипных детерминированных сигналов :

(2.8)

Подавая на вход линейной цепи (рис. 1.14), коэффициент передачи которой равен , элементарный детерминированный сигнал, можно найти элементарный отклик цепи, то есть сигнал на выходе цепи.

Рис.2.3.К определению сигнала на выходе линейной цепи.

Сигнал на выходе линейной цепи равен

(2.9)

Поскольку для линейных цепей справедлив принцип суперпозиции, то результирующий отклик будет равен:

(2.10)

Функции, описывающие элементарные сигналы, называются базисными функциями. Представление сигнала базисными функциями упрощается, если они являются ортогональными и ортонормированными.

Набор функций называется ортогональным, Если в интервале от до

при (2.11)

И ортонормированным, Если для всех Выполняется условие

. (2.12)

Ортогональность базисных функций, с помощью которых представляется исходный сигнал , является гарантией того, что представление сигнала может быть сделано единственным образом. Условию ортогональности отвечают гармонические функции кратных частот, а также функции Уолша, которые на отрезке своего существования от до принимают лишь значения, равные 1, дискретные сигналы Баркера и некоторые другие функции. Спектральный метод анализа сигналов основан на преобразованиях Фурье и состоит в замене сложной функции времени, описывающей сигнал, суммой простых гармонических сигналов, образующих частотный спектр этого сигнала. Знаменитый французский физик и математик Ж. Б. Фурье (1768 – 1830 г. г.) доказал, что любое изменение во времени некоторой функции можно аппроксимировать в виде конечной или бесконечной суммы ряда гармонических колебаний с разными амплитудами, частотами и начальными фазами. Этой функцией может быть ток или напряжение в электрической цепи.

Рассмотрим вначале представление периодического электрического сигнала (рис. 2.4), отвечающего условию

, (2.13)

где: — период сигнала; =1,2,3,….

Рис. 2.4. Периодический сигнал

Представим этот сигнал бесконечным тригонометрическим рядом:

. (2.14)

Этот ряд называется рядом Фурье.

Возможна запись ряда Фурье в другом виде:

, (2.15)

Где: — модуль амплитуд гармоник;

— фазы гармоник;

— круговая частота;

— коэффициенты косинусоидальных составляющих; — коэффициенты синусоидальных составляющих; — среднее значение сигнала за период (постоянная составляющая).

Отдельные слагаемые рядов называют гармониками. Число является номером гармоники. Совокупность величин в ряде (2.15) называют спектром амплитуд, а совокупность величин — спектром фаз.

Ниже на рис. 2.5 представлены амплитудный и фазовый спектры периодического сигнала. Вертикальные отрезки амплитудного спектра представляют амплитуды гармоник и называются спектральными линиями.

Рис 2.5. Амплитудный и фазовый спектры периодического сигнала

Таким образом, спектр периодического сигнала – Линейчатый. Каждый периодический сигнал имеет вполне определенные амплитудный и фазовый спектры.

Сумма ряда (2.15) является бесконечной, но, начиная с некоторого номера, амплитуды гармоник настолько малы, что ими можно пренебречь и практически реальный периодический сигнал представляется функцией с ограниченным спектром. Интервал частот, соответствующий ограниченному спектру, называется шириной спектра.

Если функция , описывающая периодический сигнал, является четной, то сумма ряда (2.14) будет содержать только косинусоидальные составляющие. Если — нечетная функция, то сумма будет содержать только синусоидальные составляющие.

Возможно также представление периодического сигнала в виде комплексного ряда Фурье:

, (2.16)

Где:

— комплексные амплитуды спектра, содержащие информацию, как об амплитудном, так и о фазовом спектрах.

После подстановки значений и , получим:

(2.17)

Если подставить полученное значение в ряд (1.29), то он обращается в тождество. Таким образом, периодический электрический сигнал можно задавать либо функцией времени , либо комплексной амплитудой спектра.

2.2.1. Спектр периодической последовательности прямоугольных импульсов

Состав спектра периодической последовательности прямоугольных импульсов зависит от величины отношения периода последовательности к длительности импульса, называемого скважностью импульсов. В спектре будут отсутствовать гармоники с номерами кратными скважности импульсов. Скважность импульсов равна . На рис.1.17 приведены три импульсные последовательности с разными скважностями и соответствующие им спектры. Для периодической последовательности, скважность которой равна 2, в спектре отсутствуют 2, 4, 6 ,8 и т. д. гармоники. Для последовательности, скважность которой равна 3, в спектре отсутствуют 3, 6 и т. д. гармоники. Для последовательности, скважность которой равна 4, в спектре отсутствуют 4, 8 и т. д. гармоники. Во всех приведенных спектрах интервал между спектральными линиями равен величине обратной периоду последовательности. Точки на оси частот, в которых спектр равен нулю, соответствуют величине, обратной длительности импульсов периодических последовательностей.

Рис.2.6.Периодические последовательности импульсов и их спектры.

2.2.2. Спектр непериодического сигнала

При рассмотрении спектра непериодического сигнала воспользуемся предельным переходом от периодического сигнала к непериодическому сигналу, устремив период к бесконечности.

Для периодического сигнала, представленного на рис. 2.4, ранее получено выражение (2.17) для комплексной амплитуды спектра:

(2.18)

Введем обозначение:

(2.19)

Построим модуль спектра :

Рис. 2.7. Модуль спектра периодического сигнала

Расстояние между спектральными линиями равно . Если увеличивать период , то будет уменьшаться интервал w1 . При интервал между спектральными линиями w1® dw. При этом периодическая последовательность импульсов превращается в одиночный импульс и модуль спектра стремится к непрерывной функции частоты . В результате предельного перехода от периодического сигнала к непериодическому линейчатый спектр вырождается в сплошной спектр, представленный на рис. 2.8.

Рис. 2.8. Спектр непериодического сигнала

При этом комплексная амплитуда равна:

. (2.20)

С учетом предельного перехода при

(2.21)

Подставим полученное выражение в ряд (2.16). При этом сумма трансформируется в интеграл, а значения дискретных частот в значение текущей частоты и непериодический сигнал можно представить в следующем виде:

. (2.22)

Это выражение соответствует обратному преобразованию Фурье. Огибающая сплошного спектра одиночного импульса совпадает с огибающей линейчатого спектра периодической функции, представляющей периодическое повторение этого импульса.

Интеграл Фурье позволяет любую непериодическую функцию представить в виде суммы бесконечного числа синусоидальных колебаний с бесконечно малыми амплитудами и бесконечно малым интервалом по частоте. Спектр сигнала определяется из выражения

. (2.23)

Этот интеграл соответствует прямому преобразованию Фурье.

– комплексный спектр, в нём содержится информация, как о спектре амплитуд, так и о спектре фаз.

Таким образом, спектр непериодической функции сплошной. Можно сказать, что в нём содержатся «все» частоты. Если вырезать из сплошного спектра малый интервал частот , то частоты спектральных составляющих в этом участке будут отличаться сколь угодно мало. Поэтому спектральные составляющие можно складывать так, как будто все они имеют одну и ту же частоту и одинаковые комплексные амплитуды. Спектральная плотность есть отношение комплексной амплитуды малого интервала частот к величине этого интервала.

Спектральный анализ сигналов имеет фундаментальное значение в радиоэлектронике. Информация о спектре сигнала позволяет обоснованно выбирать полосу пропускания устройств, на которые воздействует этот сигнал.

2.2.3. Спектр одиночного прямоугольного видеоимпульса

Рассчитаем спектр одиночного прямоугольного импульса, амплитуда которого равна Е, а длительность — t, представленного на рис. 2.9.

Рис. 2.9. Одиночный прямоугольный импульс

В соответствии с выражением (2.24) спектр такого сигнала равен

=. (2.24)

Поскольку = 0 , когда , то частоты, на которых спектр обращается в нуль равны , где K=1,2,3…

На рис. 2.10 представлен комплексный спектр одиночного прямоугольного импульса длительностью .

Рис.2.10. Спектр одиночного прямоугольного импульса

Спектральная плотность определяет распределение энергии в спектре одиночного импульса. В общем случае распределение энергии неоднородно. Однородное распределение характерно для хаотического процесса, называемого «белым шумом».

Спектральная плотность импульса на нулевой частоте равна его площади. Приблизительно 90% энергии одиночного прямоугольного импульса сосредоточено в спектре, ширина которого определяется выражением

. (2.25)

Соотношение (1.41) определяет требования к ширине полосы пропускания радиотехнического устройства. В задачах, где форма сигнала имеет второстепенное значение полосу пропускания устройства для этого сигнала можно выбрать равной ширине первого лепестка спектра. При этом неизвестна степень искажения формы сигнала. Двукратное увеличение полосы пропускания лишь на 5% увеличит энергию сигнала при одновременном возрастании уровня шумов.

2.2.4. Спектры неинтегрируемых сигналов

Фурье анализ применим лишь к интегрируемым функциям, то есть к функциям, для которых выполняется условие сходимости интеграла:

(2.26)

К неинтегрируемым относятся такие сигналы, как -импульс, единичный скачок, гармонический сигнал, постоянное напряжение.

Спектр — импульса

Рассчитаем спектр —Импульса с помощью интеграла прямого преобразования Фурье.

(2.27)

На основании стробирующего свойства — функции получим:

. (2.28)

Таким образом, и . При фаза .

Рис.2.11. Спектр — импульса

Итак, — функция имеет сплошной бесконечный спектр с единичной амплитудой на всех частотах. В момент возникновения импульса все гармонические составляющие бесконечного спектра складываются когерентно, поскольку спектр вещественный. В результате этого наблюдается бесконечно большая амплитуда импульса.

Спектр гармонического сигнала

Вычислим спектр гармонического сигнала с единичной амплитудой .