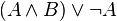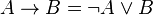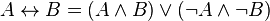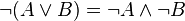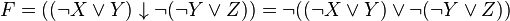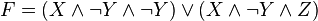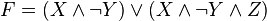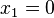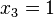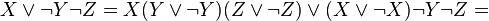Как найти днф для формул

Базис
=наиболее изучен и имеет самое широкое
применение на практике.

Определение.
Элементарной
конъюнкцией (дизъюнкцией) называется
конъюнкция (дизъюнкция) переменных или
их отрицаний.

Пример
2.3.1
–

а)
иэлементарные
дизъюнкции;

б)
иэлементарные
конъюнкции;

в)одновременно
является и элементарной дизъюнкцией и
элементарной конъюнкцией.

Определение.
Дизъюнктивной
нормальной формой (ДНФ) называется
дизъюнкция элементарных конъюнкций.
Конъюнктивной нормальной формой (КНФ)
называется конъюнкция элементарных
дизъюнкций.

Пример
2.3.2
–

а)ДНФ;

б)
КНФ.

Теорема.
Любая
формула может быть приведена к ДНФ (КНФ)
(т.е. любая формула эквивалентна некоторой
ДНФ (КНФ)).

Правило
приведения формулы к ДНФ:

а)
все логические операции, присутствующие
в формуле, выразить через
,
используя эквивалентности:

1);

2);

3);

4);

5);

б)
перенести все отрицания к переменным
по закону де Моргана:

;

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
конъюнкции выполнялись раньше дизъюнкций:
.

Пример
2.3.3
– Приведём к ДНФ формулу
.
Для этого

заменим
на,
затем применим закон де Моргана и закон
двойного отрицания:=.

Заметим,
что последняя формула в примере в
некоторых учебниках уже считается ДНФ,
в других же считают, что в элементарных
конъюнкциях и дизъюнкциях каждая
переменная должна встречаться не более
одного раза. Для удаления лишних
переменных применяют следующие
эквивалентности:

а)
(закон
идемпотентности);

б)
(закон
исключённого третьего),(закон
противоречия); в),–
( свойства констант).

Поэтому,
используя закон идемпотентности, в
последнем примере получим ДНФ:
.

Приведение
формулы к КНФ производится так же как
к ДНФ, только вместо пункта в) применяется
пункт в:

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
дизъюнкции выполнялись раньше конъюнкций,
т.е..

Пример
2.3.4
– Приведём к КНФ формулу
.

Заменим
операцию
,
используя формулу:

[закон
де Моргана, двойное

отрицание]
–
КНФ.

ДНФ
и КНФ имеют тот недостаток, что они не
обладают свойством единственности,
т.е. одна и та же формула имеет несколько
ДНФ и КНФ. Этим недостатком не обладают
совершенные нормальные формы.

Определение.
Совершенной
дизъюнктивной нормальной формой
(СДНФ)
называется ДНФ, в которой в каждую
элементарную конъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных конъюнкций не
должно быть одинаковых; совершенной
конъюнктивной нормальной формой
(СКНФ)
называется КНФ, в которой в каждую
элементарную дизъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных дизъюнкций не
должно быть одинаковых.

Пример
2.3.5
–

а)
–
СДНФ;

б)
–
СКНФ;

в)
–
не СДНФ, т.к. содержит две одинаковых
элементарных конъюнкции;

г)
–
не СДНФ, т.к. в одной элементарной
конъюнкции содержится и переменная и
её отрицание:.

Теорема.
(Существование
и единственность СДНФ и СКНФ). Всякая
логическая формула единственным образом
(с точностью до порядка следования
элементарных конъюнкций (дизъюнкций))
может быть представлена в СДНФ (СКНФ).

Для
приведения формулы к СДНФ можно
использовать один из двух методов:

І
метод: приводим формулу к ДНФ; если
какая-то элементарная конъюнкция не
содержит некоторой переменной у, то
добавляем её, используя закон расщепления:
;
убираем одинаковые элементарные
конъюнкции, используя закон идемпотентности
.

Пример
2.3.6
– Получим СДНФ функции
,
заданной в ДНФ:

–
СДНФ.

ІІ
метод:
для
данной формулы строим таблицу истинности,
потом применяем правило, основанное на
теореме Шеннона: СДНФ функции
содержит
столько элементарных конъюнкций, сколько
единиц в столбце значений;
каждому единичному набору нулей и единицсоответствует
элементарная конъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.7
– Для функции
,
заданной в ДНФ, найти СДНФ. Построим
таблицу истинности:

Т
а б л и ц а 2.3.1

0	0	0	1	1	0	1	0	0	0
0	0	1	1	1	0	1	1	0	1
0	1	0	1	0	0	0	0	0	0
0	1	1	1	0	1	0	0	1	1
1	0	0	0	1	0	0	0	1	1
1	0	1	0	1	0	0	0	1	1
1	1	0	0	0	0	0	0	1	1
1	1	1	0	0	1	0	0	1	1

Функция
принимает значение 1 при следующих
значениях аргументов:
–
это её единичные наборы. По выше
приведённому правилу,–
СДНФ.

Приведение
формулы к СКНФ аналогично приведению
к СДНФ. Также существует два метода:

а)
метод элементарных преобразований;

б)
СКНФ находят по таблице истинности:
СКНФ функции
содержит
столько элементарных дизъюнкций, сколько
нулей в столбце значений;
каждому нулевому набору нулей и единицсоответствует
элементарная дизъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.8
– Рассмотрим функцию из предыдущего
примера
.
Приведём её к СКНФ двумя способами:

а)

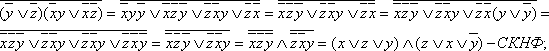
б)
из таблицы истинности выпишем нулевые
наборы:,
значит, по выше приведённому правилу,–
СКНФ.

Минимизация
булевых функций в классе ДНФ. Карты
Карно

При
решении практических задач часто
возникает проблема минимизации логических
формул, в смысле, например, найти формулу,
содержащую наименьшее число переменных,
или наименьшее число операций, или
наименьшее количество подформул
определённого вида и т.д. К настоящему
времени наиболее изучена задача отыскания
дизъюнктивных форм, минимальных по
числу вхождений переменных. Под вхождением
переменной понимается место, которое
переменная занимает в формуле.

Определение.
Минимальной
ДНФ (МДНФ) называется ДНФ с наименьшим
числом вхождений переменных.

Существует
много способов отыскания МДНФ (метод
Квайна, неопределённых коэффициентов,
с помощью гиперкубов и т.д.). Остановимся
на наиболее простом – с использованием
карт (диаграмм) Карно.

Карта
Карно
–
это таблица, каждая клетка (ячейка)
которой соответствует некоторой
элементарной конъюнкции всех переменных.
Для функции n переменных
существуетвозможных
комбинаций их значений, состоящих из 0
и 1. То есть, например, для n=2 имеемэлементарные
конъюнкции,
которым соответствуют следующие наборы
0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 –––
(1,1,1), (1,1,0),…,(0,0,0) и т.д. Карты Карно строятся
в виде таблицы размеромтак,
что её столбцы соответствуют значениям
переменных,
строки
–
(или
наоборот); вообще, для одной и той же
функции может быть построено несколько
карт, важно, чтобы соседние ячейки (как
по вертикали, так и по горизонтали)
отличались только значением одной
переменной.

Мы
будем рассматривать в основном функции
двух, трёх и четырёх переменных. Для них
карты Карно имеют следующий вид:

а)
для функции двух переменных х,
у
– рисунок 2.3.1;

б)для
функции трёх переменных
–
рисунок 2.3.2;

в)
для функции четырёх переменных
–
рисунок 2.3.3.

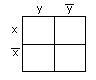
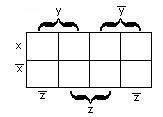
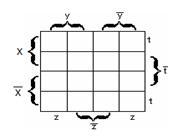
Рисунок
2.3.1 Рисунок 2.3.2 Рисунок 2.3.3

Для
определения МДНФ булевой функции,
сначала надо найти её СДНФ, затем каждую
элементарную конъюнкцию СДНФ отметить
единицей в соответствующей ячейке карты
Карно.

Пример
2.3.9
– Функции
изаданы
в форме СДНФ. Карта Карно дляна
рисунке 2.3.4; для–
на рисунке 2.3.5.

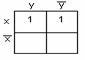
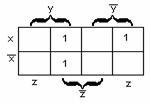
Рисунок
2.3.4 Рисунок 2.3.5

Заметим,
что, если в картах Карно две, четыре,
восемь (для функции четырёх переменных)
соседних ячеек по вертикали или по
горизонтали содержат 1, то эти ячейки
объединяют в блоки (на картах их отмечают
овалами) и соответствующие этим блокам
дизъюнкции элементарных конъюнкций
можно упростить. Так, в примере 2.3.9 для
функции
имеем
блок из двух ячеек, на рисунке он отмечен
овалом. Этому блоку соответствует
дизъюнкция,
упрощая которую, получим:.
Таким образом, блоку из двух ячеек
функции двух переменных отвечает одна
переменнаях,
а
именно та переменная, которая полностью
«покрывает» этот блок. Формула упростилась
.

Для
функции
также
имеем один блок из двух ячеек, ему
соответствует дизъюнкция элементарных
конъюнкций,
упрощая которую получим,
т.е. блоку из двух ячеек функции трёх
переменных соответствует конъюнкция
двух переменных, «покрывающих» этот
блок. Формула упростилась.

Рассмотрим
ещё несколько примеров.

Пример
2.3.10
–
–
СДНФ функции. Её карта Карно на рисунке
2.3.6. Так какz
находится на обоих концах карты, то её
(карту) можно «скрутить» и считать, что
1 в углах карты образуют блок из четырёх
ячеек. Эти четыре ячейки полностью
«покрывает» переменная z, т.о., МДНФ
функции будет
.

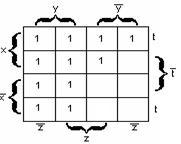
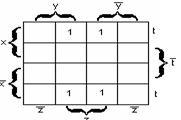
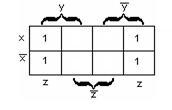
Рисунок
2.3.6 Рисунок 2.3.7 Рисунок 2.3.8

Пример
2.3.11
–
–
СДНФ функции. Её карта Карно на рисунке
2.3.7. На карте есть блок из четырёх ячеек,
который покрывают переменныеи,
поэтому МДНФ функции будет:.

Пример
2.3.12
– Карта Карно для функции

заданной
в СДНФ на рисунке 2.3.8.

На
карте имеем: блок из 8 ячеек покрывает
переменная y;
двум блокам из 4 ячеек соответствуют
элементарные конъюнкции
и,
поэтому МДНФ будет:.

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Примеры[править | править код]

Формулы в ДНФ:

Формулы не в ДНФ:

Но последние две формулы эквивалентны следующим формулам в ДНФ:

Построение ДНФ[править | править код]

Алгоритм построения ДНФ[править | править код]

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ[править | править код]

Приведем к ДНФ формулу

Выразим логическую операцию → через

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Используя закон дистрибутивности, получаем:

Используя идемпотентность конъюкции, получаем ДНФ:

k-дизъюнктивная нормальная форма[править | править код]

k-дизъюнктивной нормальной формой называют дизъюнктивную нормальную форму, в которой каждая конъюнкция содержит ровно k литералов.

Например, следующая формула записана в 2-ДНФ:

Переход от ДНФ к СДНФ[править | править код]

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Формальная грамматика, описывающая ДНФ[править | править код]

Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:

<ДНФ> → <конъюнкт>

<ДНФ> → <ДНФ> ∨ <конъюнкт>

<конъюнкт> → <литерал>

<конъюнкт> → (<конъюнкт> ∧ <литерал>)

<литерал> → <терм>

<литерал> → ¬<терм>

где <терм> обозначает произвольную булеву переменную.

Особенности обозначений[править | править код]

Следует отметить, что для удобства восприятия в качестве обозначения конъюнкции и дизъюнкции часто используют символы арифметического умножения и сложения, при этом символ умножения часто опускается. В этом случае формулы булевой алгебры выглядят как алгебраические полиномы, что более привычно для глаза, однако иногда может привести к недоразумениям.

Например, следующие записи эквивалентны:

По этой причине ДНФ в русскоязычной литературе иногда называют «суммой произведений», что является калькой с английского термина «sum of products».

См. также[править | править код]

• Конъюнктивная нормальная форма
• Совершенная дизъюнктивная нормальная форма
• Совершенная конъюнктивная нормальная форма

• Конъюнктивный одночлен
• Дизъюнктивный одночлен

Примечания[править | править код]

Литература[править | править код]

• Ю.И. Галушкина, А.Н. Марьямов: Конспект лекций по дискретной математике – 2-е изд., испр. – М.: Айрис-пресс, 2008. – 176 с. – (Высшее образование).

Ссылки[править | править код]

• ДНФ, СДНФ, КНФ, СКНФ
• Disjunctive Normal Form
• Дизъюнктивная и Конъюнктивная нормальные формы
• Определение ДНФ и КНФ

ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина

На этой странице вы найдете готовые примеры задач, связанных с упрощением и преобразованием булевых функций к нормальным формам (ДНФ, КНФ), совершенным нормальным формам (СДНФ, СКНФ) и к каноническому многочлену Жегалкина.

Самый простой метод построения совершенной дизъюнктивной и конъюнктивной нормальных форм — с помощью таблиц истинности. Для перехода к ДНФ и КНФ используют методы эквивалентных преобразований, правила де Моргана, свойства поглощения, правило Блейка и т.п.

Полином Жегалкина может быть построен как с помощью последовательных преобразований, так и по таблице истинности (метод неопределенных коэффициентов).

Все эти примеры разобраны ниже. Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.

Другие примеры решений о булевых функциях:

• Булевы формулы
• Таблицы истинности
• Минимизация ДНФ булевых функций
• Полнота системы функций

Задачи и решения о представлении булевых функций

Нормальные формы (КНФ, СКНФ, ДНФ и СДНФ): примеры решений

Задача 1. Привести к КНФ и СКНФ.

$$((((Ato B)to bar A) to bar B) to bar C).$$

Задача 2. С помощью эквивалентных преобразований построить д.н.ф. функции:

$$f(x)=(overlinex_2 oplus x_3) cdot (x_1 x_3 to x_2) $$

Задача 3. Используя СКНФ, найдите наиболее простую формулу алгебры высказываний от четырех переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:

Задача 4. Привести данные выражения к ДНФ, пользуясь правилами де Моргана. Если возможно, сократить ДНФ, используя свойство поглощения и правило Блейка.

Многочлен Жегалкина: примеры решений

Задача 5. Представив функцию формулой над множеством связок $$, преобразовать затем полученную формулу в полином Жегалкина функции $f(x)$ (используя эквивалентности):

$$f(x) = (x_1 vee x_2) cdot (x_2 | x_3)$$

Задача 6. Задана булева функция: $$ f(x_1, x_2, x_3) = overline vee ((x_1 wedge overline ) | overline)>$$ А) Построить таблицу истинности, найти двоичную форму булевой функции и привести ее к СДНФ и СКНФ.
Б) Найти многочлен Жегалкина.

Задача 7. Для заданной логической функции перейти к полиному Жегалкина.

Решение задач на заказ

Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ по любым разделам булевой алгебры, в том числе задачи по построению СДНФ, СКНФ, полинома Жегалкина на заказ. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней.

Лекция 04. Дизъюнктивные нормальные формы (ДНФ). Конъюнктивные нормальные формы (КНФ)

ЭК называется правильной, если все входящие в неё переменные различны.

Правильная ЭК называется полной относительно данного набора переменных, если в неё входят все эти переменные.

Для элементарных дизъюнкций (ЭД) – аналогичный набор определений.

ЭД – выражение вида

X1a1 V X2a2 V…V Xnan

ДНФ – дизъюнкция разных правильных элементарных конъюнкций.

X1 V X1X2 V X1X2X3 – ДНФ.

ДНФ называется совершенной (СДНФ), если все входящие в неё элементарные конъюнкции полны относительно данного набора переменных.

КНФ – конъюнкция разных правильных элементарных дизъюнкций.

СКНФ – совершенная КНФ. У нее все ЭД полны.

Любая булева функция, тождественно не равная нулю, представима и притом единственным образом в виде СДНФ по формуле:

F(x1… xn) = V(X1a1 X2a2…Xnan)

N(f) Ì N(G) – носители функции.

G(a) = G(a…an) = (aa…anan) V (…) , где пустые скобки – оставшееся выражение.

Подставив координаты, получим:

G(b..bn) = 1 – тогда, когда хотя бы одна

Первая часть доказана.

Посчитаем, сколько полных ЭК может быть

Всего – 2n = N (по перестановке комбинаций)

Число СДНФ – 2N-1 – число различных формул СДНФ.

Это число совпадает с числом различных булевых функций от n переменных (За исключением константы 0).

Так как каждой функции ставится в соответствие формула СДНФ и число разных формул и разных функций одинаково, то каждой функции соответствует только одна формула. Теорема доказана полностью.

Замечание. Единственность доказана при фиксированном числе аргументов n. Так как, вводя фиктивные переменные, мы будем менять вид формулы.

Следствие. Любая булева функция представима формулой, в которую входит только конъюнкция, дизъюнкция и отрицание.

Принцип двойственности

F*(x1…xn) – двойственная функция,

Чтобы получить вектор двойственности функции при ее табличном задании, переворачиваем таблицу на 180 градусов и берем отрицание от получившейся функции.

Теорема. Принцип двойственности.

Если F (x1…xn) является суперпозицией функций fi (i = 1. k), то двойственная к ней функция является такой же по структуре суперпозицией, но от двойственных функций.

Доказательство следует из определения двойственной функции.

F*(x1..xn) = F(x1…xn) = f(f1…fk) = f*(f1…fk)

F(x1..xn) = K1 V K2 V… V Kn – СДНФ

F*(x1..xn) = D1 D2 … Dn — СКНФ

Используя принцип двойственности, можно доказать следующую теорему.

Любая булева функция, тождественно не равная единице представима и притом единственным образом в виде СКНФ.

Доказательство получается из самого принципа двойственности и его следствий.

Задача минимизации ДНФ.

1. Рангом правильной ЭК называется число разных переменных, входящих в нее.

2. Рангом ДНФ называется сумма рангов всех ЭК, входящих в ДНФ.

3. Минимальной ДНФ или Dmin для данной функции называется ДНФ, которая равна этой функции и имеет наименьший ранг.

Задача минимизации ДНФ для данной функции состоит в нахлждении минимальной ДНФ.

Число ДНФ при фиксированном n – конечное (n — число переменных)

Тривиальный алгоритм минимизации ДНФ состоит в следующем:

1. Выписываем все возможные ДНФ от данного числа n в порядке возрастания их рангов.

2. Последовательно сравниваем нашу функцию с каждой из этих ДНФ. Первая ДНФ, которой равна наша функция имеет минимальный ранг.

Алгоритм представления функции в виде СДНФ.

1. Выписываем носитель функции.

2. Для каждого вектора из носителя выписываем конъюнкцию соответствующих переменных. (если координата равна нулю, переменную пишем с отрицанием, если единице – без отрицания). Это и будут все полные ЭК.

3. Выписываем дизъюнкцию всех этих ЭК.

Алгоритм представления функции в виде СКНФ.

1. Выписываем носитель функции

2. Для каждого вектора из носителя выписываем дизъюнкцию соответствующих переменных. (если координата равна нулю, переменную пишем без отрицания, . если единице – с отрицанием). Это и будут все полные ЭД.

Дизъюнктивная и конъюнктивная совершенные нормальные формы

Для всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).

Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.

Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).

Совершенная дизъюнктивная нормальная форма (СДНФ)

Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.

Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.

ДНФ записывается в следующей форме: F₁ ∨ F₂ ∨ . ∨ F_n, где F_i — элементарная конъюнкция

Определение. Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой конъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.

Совершенная конъюнктивная нормальная форма (СКНФ)

Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.

Определение. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.

КНФ записывается в следующей форме: F₁ ∧ F₂ ∧ . ∧ F_n, где F_i — элементарная дизъюнкция

Определение. Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х₁, х₂, …, х_k, причем на i-м месте этой дизъюнкции стоит либо переменная х_i, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.

Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ .

Алгоритм построения СДНФ по таблице истинности

1. Выбрать все строки таблицы, в которых значение функции равно единице.
2. Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.

Алгоритм построения СКНФ по таблице истинности

1. Выбрать все строки таблицы, в которых значение функции равно нулю.
2. Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные дизъюнкции связываем операциями конъюнкции.

Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае — СКНФ.

Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.

x	y	z	F (x, y, z)
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Т.к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)

Проверим полученную формулу. Для этого построим таблицу истинности функции.

x	y	z	¬ x	¬ x ∨ y ∨ z	¬ z	¬ x ∨ y ∨ ¬ z	F (x, y, z)
0	0	0	1	1	1	1	1
0	0	1	1	1	0	1	1
0	1	0	1	1	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	0	1	1	0
1	0	1	0	1	0	0	0
1	1	0	0	1	1	1	1
1	1	1	0	1	0	1	1

Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают. Значит, логическая функция построена верно.

Дизъюнктивная нормальная форма

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.

Формулы в ДНФ:

Формулы не в ДНФ:

Алгоритм построения ДНФ

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ

Приведем к ДНФ формулу :

Выразим логические операции → и ↓ через :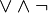

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Совершенная дизъюнктивная нормальная форма

Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных конъюнкций
• в каждой конъюнкции нет одинаковых пропозициональных букв
• каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Для любой функции алгебры логики существует своя СДНФ, причём единственная.

Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:

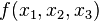0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

В ячейках результата 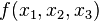 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.

Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:

• 
• 
• 

Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 

Переменные второго члена:

• 
• 
• 

 в этом случае будет представлен без инверсии: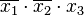 

Таким образом анализируются все ячейки 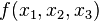. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).

Совершенная ДНФ этой функции:

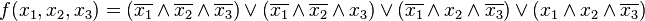
Переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

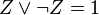после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как  по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.