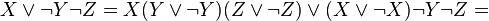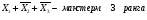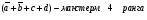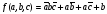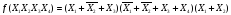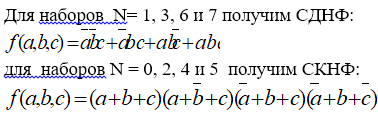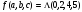Как найти днф для формулы

Базис
=наиболее изучен и имеет самое широкое
применение на практике.

Определение.
Элементарной
конъюнкцией (дизъюнкцией) называется
конъюнкция (дизъюнкция) переменных или
их отрицаний.

Пример
2.3.1
–

а)
иэлементарные
дизъюнкции;

б)
иэлементарные
конъюнкции;

в)одновременно
является и элементарной дизъюнкцией и
элементарной конъюнкцией.

Определение.
Дизъюнктивной
нормальной формой (ДНФ) называется
дизъюнкция элементарных конъюнкций.
Конъюнктивной нормальной формой (КНФ)
называется конъюнкция элементарных
дизъюнкций.

Пример
2.3.2
–

а)ДНФ;

б)
КНФ.

Теорема.
Любая
формула может быть приведена к ДНФ (КНФ)
(т.е. любая формула эквивалентна некоторой
ДНФ (КНФ)).

Правило
приведения формулы к ДНФ:

а)
все логические операции, присутствующие
в формуле, выразить через
,
используя эквивалентности:

1);

2);

3);

4);

5);

б)
перенести все отрицания к переменным
по закону де Моргана:

;

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
конъюнкции выполнялись раньше дизъюнкций:
.

Пример
2.3.3
– Приведём к ДНФ формулу
.
Для этого

заменим
на,
затем применим закон де Моргана и закон
двойного отрицания:=.

Заметим,
что последняя формула в примере в
некоторых учебниках уже считается ДНФ,
в других же считают, что в элементарных
конъюнкциях и дизъюнкциях каждая
переменная должна встречаться не более
одного раза. Для удаления лишних
переменных применяют следующие
эквивалентности:

а)
(закон
идемпотентности);

б)
(закон
исключённого третьего),(закон
противоречия); в),–
( свойства констант).

Поэтому,
используя закон идемпотентности, в
последнем примере получим ДНФ:
.

Приведение
формулы к КНФ производится так же как
к ДНФ, только вместо пункта в) применяется
пункт в:

в)
используя закон дистрибутивности,
преобразовать формулы так, чтобы все
дизъюнкции выполнялись раньше конъюнкций,
т.е..

Пример
2.3.4
– Приведём к КНФ формулу
.

Заменим
операцию
,
используя формулу:

[закон
де Моргана, двойное

отрицание]
–
КНФ.

ДНФ
и КНФ имеют тот недостаток, что они не
обладают свойством единственности,
т.е. одна и та же формула имеет несколько
ДНФ и КНФ. Этим недостатком не обладают
совершенные нормальные формы.

Определение.
Совершенной
дизъюнктивной нормальной формой
(СДНФ)
называется ДНФ, в которой в каждую
элементарную конъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных конъюнкций не
должно быть одинаковых; совершенной
конъюнктивной нормальной формой
(СКНФ)
называется КНФ, в которой в каждую
элементарную дизъюнкцию каждая переменная
входит ровно один раз, причём, входит
либо сама переменная, либо её отрицание,
и среди элементарных дизъюнкций не
должно быть одинаковых.

Пример
2.3.5
–

а)
–
СДНФ;

б)
–
СКНФ;

в)
–
не СДНФ, т.к. содержит две одинаковых
элементарных конъюнкции;

г)
–
не СДНФ, т.к. в одной элементарной
конъюнкции содержится и переменная и
её отрицание:.

Теорема.
(Существование
и единственность СДНФ и СКНФ). Всякая
логическая формула единственным образом
(с точностью до порядка следования
элементарных конъюнкций (дизъюнкций))
может быть представлена в СДНФ (СКНФ).

Для
приведения формулы к СДНФ можно
использовать один из двух методов:

І
метод: приводим формулу к ДНФ; если
какая-то элементарная конъюнкция не
содержит некоторой переменной у, то
добавляем её, используя закон расщепления:
;
убираем одинаковые элементарные
конъюнкции, используя закон идемпотентности
.

Пример
2.3.6
– Получим СДНФ функции
,
заданной в ДНФ:

–
СДНФ.

ІІ
метод:
для
данной формулы строим таблицу истинности,
потом применяем правило, основанное на
теореме Шеннона: СДНФ функции
содержит
столько элементарных конъюнкций, сколько
единиц в столбце значений;
каждому единичному набору нулей и единицсоответствует
элементарная конъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.7
– Для функции
,
заданной в ДНФ, найти СДНФ. Построим
таблицу истинности:

Т
а б л и ц а 2.3.1

0	0	0	1	1	0	1	0	0	0
0	0	1	1	1	0	1	1	0	1
0	1	0	1	0	0	0	0	0	0
0	1	1	1	0	1	0	0	1	1
1	0	0	0	1	0	0	0	1	1
1	0	1	0	1	0	0	0	1	1
1	1	0	0	0	0	0	0	1	1
1	1	1	0	0	1	0	0	1	1

Функция
принимает значение 1 при следующих
значениях аргументов:
–
это её единичные наборы. По выше
приведённому правилу,–
СДНФ.

Приведение
формулы к СКНФ аналогично приведению
к СДНФ. Также существует два метода:

а)
метод элементарных преобразований;

б)
СКНФ находят по таблице истинности:
СКНФ функции
содержит
столько элементарных дизъюнкций, сколько
нулей в столбце значений;
каждому нулевому набору нулей и единицсоответствует
элементарная дизъюнкция всех переменных,
в которойвзято
с отрицанием, еслии
без отрицания, если.

Пример
2.3.8
– Рассмотрим функцию из предыдущего
примера
.
Приведём её к СКНФ двумя способами:

а)

б)
из таблицы истинности выпишем нулевые
наборы:,
значит, по выше приведённому правилу,–
СКНФ.

Минимизация
булевых функций в классе ДНФ. Карты
Карно

При
решении практических задач часто
возникает проблема минимизации логических
формул, в смысле, например, найти формулу,
содержащую наименьшее число переменных,
или наименьшее число операций, или
наименьшее количество подформул
определённого вида и т.д. К настоящему
времени наиболее изучена задача отыскания
дизъюнктивных форм, минимальных по
числу вхождений переменных. Под вхождением
переменной понимается место, которое
переменная занимает в формуле.

Определение.
Минимальной
ДНФ (МДНФ) называется ДНФ с наименьшим
числом вхождений переменных.

Существует
много способов отыскания МДНФ (метод
Квайна, неопределённых коэффициентов,
с помощью гиперкубов и т.д.). Остановимся
на наиболее простом – с использованием
карт (диаграмм) Карно.

Карта
Карно
–
это таблица, каждая клетка (ячейка)
которой соответствует некоторой
элементарной конъюнкции всех переменных.
Для функции n переменных
существуетвозможных
комбинаций их значений, состоящих из 0
и 1. То есть, например, для n=2 имеемэлементарные
конъюнкции,
которым соответствуют следующие наборы
0 и 1: (1,1), (1,0), (0,1), (0,0); для n=3 –––
(1,1,1), (1,1,0),…,(0,0,0) и т.д. Карты Карно строятся
в виде таблицы размеромтак,
что её столбцы соответствуют значениям
переменных,
строки
–
(или
наоборот); вообще, для одной и той же
функции может быть построено несколько
карт, важно, чтобы соседние ячейки (как
по вертикали, так и по горизонтали)
отличались только значением одной
переменной.

Мы
будем рассматривать в основном функции
двух, трёх и четырёх переменных. Для них
карты Карно имеют следующий вид:

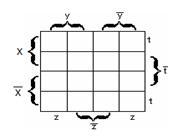
а)
для функции двух переменных х,
у
– рисунок 2.3.1;

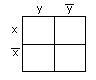
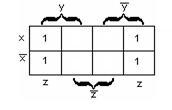
б)для
функции трёх переменных
–
рисунок 2.3.2;

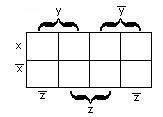
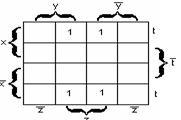
в)
для функции четырёх переменных
–
рисунок 2.3.3.

Рисунок
2.3.1 Рисунок 2.3.2 Рисунок 2.3.3

Для
определения МДНФ булевой функции,
сначала надо найти её СДНФ, затем каждую
элементарную конъюнкцию СДНФ отметить
единицей в соответствующей ячейке карты
Карно.

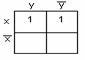
Пример
2.3.9
– Функции
изаданы
в форме СДНФ. Карта Карно дляна
рисунке 2.3.4; для–
на рисунке 2.3.5.

Рисунок
2.3.4 Рисунок 2.3.5

Заметим,
что, если в картах Карно две, четыре,
восемь (для функции четырёх переменных)
соседних ячеек по вертикали или по
горизонтали содержат 1, то эти ячейки
объединяют в блоки (на картах их отмечают
овалами) и соответствующие этим блокам
дизъюнкции элементарных конъюнкций
можно упростить. Так, в примере 2.3.9 для
функции
имеем
блок из двух ячеек, на рисунке он отмечен
овалом. Этому блоку соответствует
дизъюнкция,
упрощая которую, получим:.
Таким образом, блоку из двух ячеек
функции двух переменных отвечает одна
переменнаях,
а
именно та переменная, которая полностью
«покрывает» этот блок. Формула упростилась
.

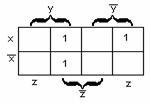
Для
функции
также
имеем один блок из двух ячеек, ему
соответствует дизъюнкция элементарных
конъюнкций,
упрощая которую получим,
т.е. блоку из двух ячеек функции трёх
переменных соответствует конъюнкция
двух переменных, «покрывающих» этот
блок. Формула упростилась.

Рассмотрим
ещё несколько примеров.

Пример
2.3.10
–
–
СДНФ функции. Её карта Карно на рисунке
2.3.6. Так какz
находится на обоих концах карты, то её
(карту) можно «скрутить» и считать, что
1 в углах карты образуют блок из четырёх
ячеек. Эти четыре ячейки полностью
«покрывает» переменная z, т.о., МДНФ
функции будет
.

Рисунок
2.3.6 Рисунок 2.3.7 Рисунок 2.3.8

Пример
2.3.11
–
–
СДНФ функции. Её карта Карно на рисунке
2.3.7. На карте есть блок из четырёх ячеек,
который покрывают переменныеи,
поэтому МДНФ функции будет:.

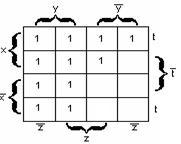
Пример
2.3.12
– Карта Карно для функции

заданной
в СДНФ на рисунке 2.3.8.

На
карте имеем: блок из 8 ячеек покрывает
переменная y;
двум блокам из 4 ячеек соответствуют
элементарные конъюнкции
и,
поэтому МДНФ будет:.

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Примеры[править | править код]

Формулы в ДНФ:

Формулы не в ДНФ:

Но последние две формулы эквивалентны следующим формулам в ДНФ:

Построение ДНФ[править | править код]

Алгоритм построения ДНФ[править | править код]

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ[править | править код]

Приведем к ДНФ формулу

Выразим логическую операцию → через

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Используя закон дистрибутивности, получаем:

Используя идемпотентность конъюкции, получаем ДНФ:

k-дизъюнктивная нормальная форма[править | править код]

k-дизъюнктивной нормальной формой называют дизъюнктивную нормальную форму, в которой каждая конъюнкция содержит ровно k литералов.

Например, следующая формула записана в 2-ДНФ:

Переход от ДНФ к СДНФ[править | править код]

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Формальная грамматика, описывающая ДНФ[править | править код]

Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:

<ДНФ> → <конъюнкт>

<ДНФ> → <ДНФ> ∨ <конъюнкт>

<конъюнкт> → <литерал>

<конъюнкт> → (<конъюнкт> ∧ <литерал>)

<литерал> → <терм>

<литерал> → ¬<терм>

где <терм> обозначает произвольную булеву переменную.

Особенности обозначений[править | править код]

Следует отметить, что для удобства восприятия в качестве обозначения конъюнкции и дизъюнкции часто используют символы арифметического умножения и сложения, при этом символ умножения часто опускается. В этом случае формулы булевой алгебры выглядят как алгебраические полиномы, что более привычно для глаза, однако иногда может привести к недоразумениям.

Например, следующие записи эквивалентны:

По этой причине ДНФ в русскоязычной литературе иногда называют «суммой произведений», что является калькой с английского термина «sum of products».

См. также[править | править код]

• Конъюнктивная нормальная форма
• Совершенная дизъюнктивная нормальная форма
• Совершенная конъюнктивная нормальная форма

• Конъюнктивный одночлен
• Дизъюнктивный одночлен

Примечания[править | править код]

Литература[править | править код]

• Ю.И. Галушкина, А.Н. Марьямов: Конспект лекций по дискретной математике – 2-е изд., испр. – М.: Айрис-пресс, 2008. – 176 с. – (Высшее образование).

Ссылки[править | править код]

• ДНФ, СДНФ, КНФ, СКНФ
• Disjunctive Normal Form
• Дизъюнктивная и Конъюнктивная нормальные формы
• Определение ДНФ и КНФ

Дизъюнктивная нормальная форма

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.

Формулы в ДНФ:

Формулы не в ДНФ:

Алгоритм построения ДНФ

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ

Приведем к ДНФ формулу :

Выразим логические операции → и ↓ через :

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Совершенная дизъюнктивная нормальная форма

Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных конъюнкций
• в каждой конъюнкции нет одинаковых пропозициональных букв
• каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Для любой функции алгебры логики существует своя СДНФ, причём единственная.

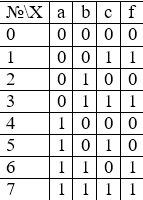
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:

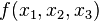0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

В ячейках результата 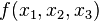 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.

Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:

• 
• 
• 

Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 

Переменные второго члена:

• 
• 
• 

 в этом случае будет представлен без инверсии: 

Таким образом анализируются все ячейки 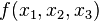. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).

Совершенная ДНФ этой функции:

Переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как  по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Логические функции, СДНФ СКНФ

1.4 Формы представления функций алгебры логики

Функции алгебры логики могут быть заданы различными способами:

– таблицей истинности – в аналитической форме- в числовой форме..

Если функция имеет значения на всех наборах, то она называется полностью определенной.

элементарная дизъюнкция – дизъюнктивный терм или макстерм – это дизъюнктивный терм или макстерм – это дизъюнкция произв числа попарно независимых перем Например,

элементарная конъюнкция – конъюнктивный терм или минтерм – конъюнкция произв числа попарно независимых перем. Напр, Х ₁Х ₂ Х₃ – минтерм 3-его ранг

– это не минтерм, так как перем и зависимы.

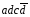
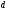
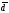
Для аналитической записи функций используют две формы:

1) Дизъюнктивную Нормальную Форму – ДНФ

2) Конъюнктивную Нормальную Форму – КНФ

ДНФ это дизъюнкция минтермов разл ранга

КНФ это конъюнкция макстермов различного ранга

Если все термы, входяшие в нормальную форму имеют одинаковый и максимальный ранг,= числу переменных функции – n, то такая форма называется совершенной. При этом, минтерм называют констинтуентой (составля) 1 (КЕ), а макстерм – конституентой 0 (КН).

– это СДНФ

– это СКНФ

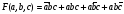
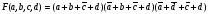
Т е СДНФ есть дизъюнкция конституент 1, а СКНФ – есть конъюнкция конституент 0

Составление совершенных форм по табл истинности

Совершенные формы составляют по табл истинности функции. СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.

СКНФ =для каждого набора переменных, на которых функция=0, записывают макстерм ранга n, в кот с отрицанием берутся переменные, имеющие значение=1 на данном наборе. Все макстермы объединены конъюнктивно

Для компактной записи функций исп числовую форму, в которой заданы только номера наборов. Числовая форма для СДНФ: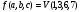

Числовая форма для СКНФ:

Алгоритм преобразованияя в ДНФ

1) Сначала избавляемся от операций импликации, эквивалентности и неравнозначности, выразив их через логические связки ¬, & и ∨ по законам:

2) Доводят знаки отрицания до независимых переменных, используя законы де Моргана:

3) Применяя з-н дистрибутивности

преобразуют формулу к дизъюнкции элементарных конъюнкций

4) 4) Постоянно избавляются от двойных отрицаний:
ДНФ A наз совершенной и обозн СДНФ, если каждая переменная формулы A входит с отрицанием или без отрицания в каждый конъюнкт точно 1 раз.

Алгебраическая форма представления булевых функций используется для минимизации (упрощения формулл) и для построения логических схем. Существукт 2 формы алгебраических функций – дизъюнктивная и конъюнктивн. Дизъюнктивная нормальная форма представляет сумму элементарных произведения аргументов, например

Если кажд слаг содер все арг или их отриц, то получ соверш дизъюнкт норм форму (СДФН), напр

Для перехода от табл истинн к СДНФ учит только те сост, для кот функц= 1. Для каждого такого сост запис элем произв всех ар. Если арг имеет зн “0”, то запис его отриц. Для привед примера СДНФ имеет вид   (17.4)

Совершенная конъюнктивная нормальная форма (СКНФ) представляет логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например

ДНФ, но не СДНФ от 3 перем

-ДНФ от 2 перем

-представл импликации в виде ДНФ.

-СДНФ для импликации

-СДНФ для оп эквивалентности

-СДНФ для оп неравнозначности

Прим.1 Привести к ДНФ формулу

Реш.

2. Привести ту же формулу к СДНФ. Начав преобразования с ДНФ

Нахождение СДНФ по табл истинности функции	Нахождение СКНФ по табл истинности функции
1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 1. 2)Выписать для каждой отмеченной строки конъюнкцию всех переменных так: если значение некоторой переменной в данной строке – 1, то в конъюнкцию включать саму эту переменную, если равно 1, то ее отрицание. 3)Все полученные конъюнкции связать в дизъюнкцию.	1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 0. 2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных так: если значение некоторой переменной в данной строке= 1, то в дизъюнкцию включать саму эту переменную, если равно 0, то ее отрицание. 3)Все полученные дизъюнкции связать в конъюнкцию.

Прим1

Прим 2

построение СДНФ:	построение СКНФ:

Для перехода от таблицы истинности к СКНФ учитывают только те состояния, для которых функция= “0”. Для каждого такого состояния записывается элементарная сумма аргументов. Если аргуент имеет значение “1”, то пишут его отрицание. Для примера СКНФ имеет вид

Примеры

1)Привести к КНФ и СКНФ.

Реш. упростим выражение, используя законы де Моргана и правило x y x y → = ∨

Теперь приводим к КНФ

Приведем к СКНФ:

2) С помощью эквивалентных преобразований построить д.н.ф. функции f (x):

Решение. Преобразуем функцию:

3) Используя СКНФ, найти наиболее простую формулу алгебры высказываний от 4 переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:

Решение. Запишем СКНФ функции по данным задачи

Получили

ЛИТЕРАТУРА и ССЫЛКИ

1)Курилова М.Н. Информатика-логика, СПБ Лес-техн ун-т им.Кирова

https://studfiles.net/preview/2069515/page:5/

2) http://ptca.narod.ru/lec/lec4_3.html

3) https://www.matburo.ru/ex_dm.php?p1=bfpg
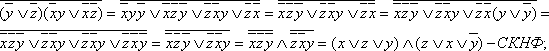
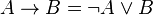
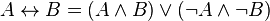
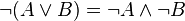
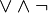
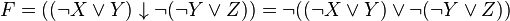
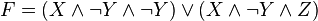
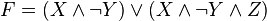
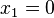
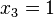
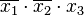
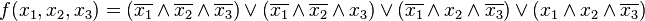
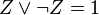