Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом 
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Теория[править | править код]
Общая формула для добротности любой колебательной системы[1]:
,
где
— резонансная круговая частота колебаний
— резонансная частота колебаний
— энергия, запасённая в колебательной системе
— рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для последовательного колебательного контура в RLC-цепях, в котором все три элемента включены последовательно:
где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно, а 

Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно:

Формулировка частотного отклика или ширины полосы пропускания колебательной системы

ЛАФЧХ колебательных звеньев с разной добротностью
В данном случае R является входным сопротивлением параллельного контура. Однако практически для электрической цепи гораздо проще измерить ток или напряжение, чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды колебаний, ширина полосы частот на АЧХ определяется на высоте 




где δ — логарифмический декремент затухания, равный отношению полуширины резонансной кривой к частоте резонанса, 
Для электрически малых антенн добротность можно определить соотношением[1]:
,
где
— резонансная круговая частота электромагнитных колебаний
— энергия электрического поля, запасённая в антенне
— энергия магнитного поля, запасённая в антенне
— рассеиваемая антенной мощность.
Метрологические аспекты[править | править код]
Для измерения электрической добротности на частотах до десятков и сотен мегагерц применяют измеритель добротности или измеритель иммитанса (косвенным способом), в диапазоне СВЧ применяются специальные методы.
См. также[править | править код]
Измеритель добротности
Примечания[править | править код]
- ↑ 1 2 Слюсар В. И. 60 лет теории электрически малых антенн. Некоторые итоги // Электроника: наука, технология, бизнес. — 2006. — Вып. 7. — С. 10—19.
Литература[править | править код]
- Бидерман В. Л. Теория механических колебаний. — Высшая школа, 1980. — 408 с. — 10 000 экз.
- Горелик Г. С. Колебания и волны. — М.: ГИФМЛ, 1959. — 572 с.
Ссылки[править | править код]
- ГПЭ единицы электрической добротности. ФГУП «СНИИМ». Дата обращения: 12 февраля 2015.
Что такое добротность контура
Электрическая цепь — предназначена не только для передачи тока и напряжения от источника к потребителю. В данной электроцепи возникают определенные физические процессы, которые связаны с влиянием ее элементов на протекание данного тока.

В этой статье будет описано, что такое добротность контура. Кроме того будет приведена формула для расчета этой величины, схемы последовательного и параллельного контуров.
Определение
Физика дает следующее определение добротности. Добротностью называют параметр колебательной системы, который определяет ширину резонанса и характеризует, насколько запасы энергии в системе больше возникающих ее потерь во время изменения фазы на один радиан. Дело в том, что данный показатель определяет разницу вынужденных колебаний при резонансе с определенной амплитудой колебаний на каком-то удалении от места резонанса. При этом амплитуда вынужденных колебаний не имеет никакой зависимости от их частоты. Параметр находит применение не только при расчетах электрических цепей. Его применяют так же в механике, акустике и химии.
Добротность колебательной системы в англоязычных ресурсах называют Quality factor и обозначают буквой «Q». Данная величина является основной характеристикой всех колебательных систем, но сделать измерения данной величины невозможно, ведь ее можно только вычислить, используя различные формулы. Степень идеальности имеет прямое влияние на коэффициент потерь энергии за время одного колебательного периода. Чем меньше величина, тем выше потери самой энергии. Данное значение обратно пропорционально скорости затухания собственных колебаний системы.

Получается, что колебательный контур является разницей между входящим реактивным сопротивлением и выходящим активным. Если в колебательном контуре имеется емкость C, индуктивность L и нагрузка R, то для расчета Q используется формула:
В данной формуле за резонансную частоту электроцепи ω0 отвечает показатель 1/R.
Параметр добротности измеряется при настройке генератора электросигналов на частоту резонансных колебаний. Сама частота резонанса равна максимальному выходному напряжению такой цепи.
Параллельный контур
Добротность любого параллельного колебательного контура предполагает наличие цепи, в которой имеется емкость, нагрузка и индуктивность, соединенные параллельно. Они образуют так называемую RLC-схему.

Определяющая величина для такой схемы — это проводимость конденсатора с катушкой. Именно она суммируется при расчетах и является реактивной проводимостью параллельного колебательного контура. На резонансной частоте проводимость катушки с конденсатором будут равны, а общая разница при этом равняется 0. Для расчета такой цепи используется формула:

При этом стоит учитывать следующее:
- Не принимается во внимание емкостная паразитная характеристика катушки индуктивности, но учитывается добротность индуктивного элемента. Она соответствует выражению:

- Также учитывается добротность конденсатора, использующегося в такой электроцепи. Потери в конденсаторе связаны с наличием диэлектрика в его конструкции. Добротность конденсатора вместе с имеющимися потерями, напрямую связаны с потерями энергии на его диэлектрике tgδ. Данный коэффициент определяем с помощью такого выражения:

- На резонансной частоте к переменному току прилагается бесконечное сопротивление.
- В реальной RLC-цепи отсутствует бесконечное сопротивление, но этот параметр при увеличении сопротивления контура значительно снижается.
В параллельном колебательном контуре резонансная частота является той частотой, при которой реактивное сопротивление равняется 0, а величина входящего сопротивления является активным. Отсюда можно сделать вывод, что отсутствует фазовый сдвиг между током и напряжением.
Последовательный контур
Для последовательного колебательного контура характерно наличие последовательного соединения емкости с индуктивностью. При этом эти два элемента не влияют на потери энергии в цепи и являются идеальными элементами.

Потери в данной схеме вызваны только наличием активной нагрузки. Ниже представлен график амплитудно-частотной характеристики такой схемы.

Для такой цепи сопротивление катушки и конденсатора являются паразитными, приводят к появлению резонанса. Данный резонанс выравнивает или обнуляет сопротивления, оставляя только влияние активной нагрузки R от резистора. При этом добротность такой электроцепи определяется, как разницу напряжений на источнике тока и выходах катушки/конденсатора. В этом случае Q определяют с помощью следующего выражения:

В данной формуле:
- С — емкость конденсатора.
- L — индуктивность катушки.
- R — потери сопротивления.
Для примера попробуем решить следующую задачу. В цепи имеется катушка индуктивности L=100 мГн с сопротивлением R=100 Ом, которая соединена последовательно с конденсатором емкостью C=0.07 мкФ. Найдите резонансную частоту ω0, характеристическое сопротивление и добротность колебательного контура.
Вычисляем резонансную частоту контура:

Определяем характеристическое сопротивление:

Конечный шаг — вычисление добротности контура:

Заключение
В статье было дано краткое описание, что такое добротность контура и чему параметр равен для различных вариантов контура (параллельного, последовательного). Данная характеристика цепи и ее составных элементов играет ключевое значение при определении потерь от включения в нее различных конденсаторов, катушек и активных резисторов. С помощью добротности можно определить разницу между входным и выходным напряжениями электроцепи.
Видео по теме
Что такое добротность колебательного контура?
как измерить добротность в радиолюбительских условиях.
«Добротность обозначается символом Q (от английского quality factor) и является тем параметром колебательной системы,
который определяет ширину резонанса и характеризует, во сколько раз запасы энергии в системе больше, чем потери энергии за
время изменения фазы на 1 радиан.
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность
колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания
»
– авторитетно учит нас Википедия.
Да уж. Напустили тумана ироды – без поллитры не разберёшься. А ведь придётся, раз впряглись.
Для начала возьмём ёжика. Хорошее животное! Хотя выдающимся умом не обладает, но думаю, что и оно в курсе, что
“quality factor” – это показатель качества колебательного контура и в первую очередь, конструктивного качества катушки индуктивности.
Теперь возьмём женщину в теле – добротную женщину. Таких женщин рисовали художники 18-го, 19-го веков, а поэты писали: «Её
выпуклости меня восхищают, её впуклости сводят с ума».
Так вот. К чему это я?
А к тому, что для получения в сухом остатке высокодобротного колебательного контура, придётся поискать в загашнике и высококачественный
конденсатор с низким током утечки, и катушку индуктивности – крепкую, добротную и красивую, словно выпавшую из картины
венецианского мастера в Пушкинском музее.
Приведём эквивалентную схему колебательного контура.
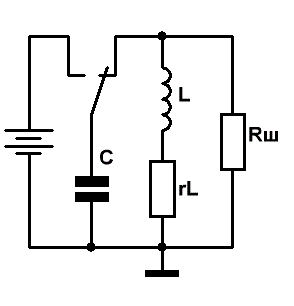
Здесь L и C – собственные индуктивность и ёмкость компонентов, входящих в состав колебательного
контура,
rL – сопротивление катушки, эквивалентное потерям электрической энергии в проводе катушки индуктивности,
Rш – сумма сопротивлений, обусловленных потерями в изоляции провода, каркасе, экране, сердечнике катушки индуктивности,
а также потерями, вызванные наличием токов утечки в конденсаторе.
Рис.1
При подключении к контуру внешних цепей, параллельно Rш добавляется дополнительное сопротивление Rн, вносимое этими внешними цепями.
По большому счёту, на Рис.1 не хватает ещё одной ёмкости, равной сумме паразитных ёмкостей катушки индуктивности, внешних цепей и
паразитной ёмкости монтажа. На высоких частотах эти привнесённые ёмкости могут иметь существенные величины, соизмеримые с ёмкостью самого
контурного конденсатора. На добротность эти ёмкости существенного влияния не оказывают, но при расчёте резонансной частоты их необходимо
учитывать и суммировать со значением основной ёмкости С.
Теперь давайте разберёмся, что такое “скорость затухания собственных колебаний в системе” и, каким боком она связана с добротностью.
Для начала мысленно спаяем схему, нарисованную на Рис.1, и замкнём переключатель на батарейку (в левое по схеме положение).
Конденсатор С зарядится до уровня, равного напряжению питания.
Теперь перещёлкнем переключатель в правое по схеме положение.
Благодаря энергии, запасённой в конденсаторе, в образовавшейся LC-цепи возникнут свободные колебания на частоте резонанса
колебательного контура, равной fо= 1/2π√LС.
Поскольку у нас ни с какой стороны не вечный двигатель – свободные колебания затухают, причём скорость затухания зависит от потерь
в конденсаторе и катушке индуктивности: чем они меньше, тем медленнее затухание.

Число колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раза,
как раз и будет числено равняться добротности контура Q.
Число периодов свободных колебаний в контуре можно подсчитать счётчиком импульсов и таким образом узнать добротность
колебательного контура, генератор сигналов в этом случае не нужен.
Собственно говоря, на таком принципе и строится большинство промышленных измерителей добротности.
Вспоминаем дальше: «Добротность является тем параметром колебательной системы, который определяет ширину резонанса».
Рисуем резонансную кривую (амплитудно частотную характеристику) колебательного контура.
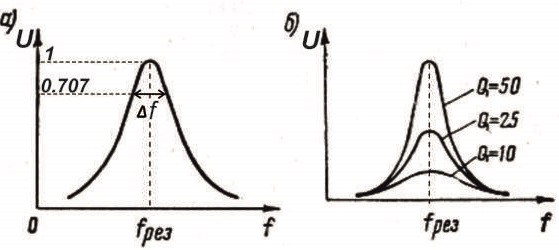
По частотной характеристике условно определяется полоса пропускания контура Δf.
При этом сделано допущение, что напряжение внутри этой полосы имеет право снижаться до уровня 0,707 от максимального.
Исходя из этого, формула для определения добротности приобретает следующий вид:
Q = f рез/Δf
.
Рис.2
Из формулы естественным образом вытекает, что чем выше добротность – тем уже полоса пропускания резонансного контура,
соответственно, чем ниже – тем шире.
А как измерить добротность контура, не прибегая к изготовлению специальных устройств, в домашней лаборатории?
1. Если речь идёт о низких (звуковых) частотах, то тут всё просто.
В этом случае, Q равна отношению реактивного сопротивления индуктивного или ёмкостного характера (характеристического сопротивления)
к полному последовательному сопротивлению потерь в резонансном контуре. В виду того, что конденсаторы на данных частотах практически не
вносят потерь, то добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления
катушки.
А поскольку данное сопротивление можно легко измерить обычным омметром, то имеет полный смысл проделать эту не сильно замысловатую
манипуляцию, после чего перейти на страницу ссылка на страницу и в первой таблице произвести расчёт
добротности. Естественным образом, подразумевается, что катушка намотана на соответствующем для данных частот сердечнике, не вносящих
существенных потерь в работу колебательного контура.
2. На высоких частотах (радиочастотах) значение активного сопротивления катушки может составлять доли ома, к
тому же возможно проявление влияния добротности конденсатора на общую добротность цепи, поэтому такими же примитивными
методами, как в случае НЧ обойтись не удастся.
Рискну сделать осторожное предположение, что в радиолюбительской лаборатории у нас затерялся высокочастотный генератор с 50-омным
выходом и такой же высокочастотный осциллограф, или, на худой конец, измеритель ВЧ напряжений.
В этом случае мы воспользуемся ещё одним определением Q. Добротность резонансного контура равна фактору увеличения напряжения и
может быть выражена отношением напряжения, развиваемого на реактивных элементах к входному напряжению, поданному последовательно с
контуром.
Спаяем пару резисторов.
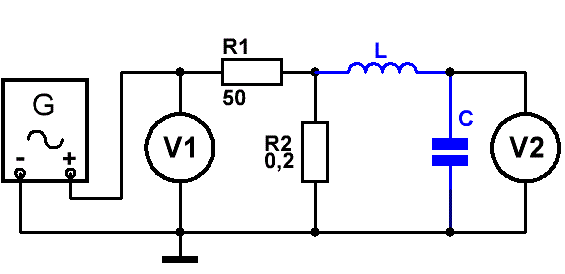
Добротность измеряется при настройке генератора сигналов на частоту резонанса контура, соответствующую максимальному выходному
напряжению.
Добротность Q рассчитывается как отношение выходного напряжения на резонансном контуре к напряжению, поданному на него.
В нашем случае
Q = 250
x V2/V1 .
Рис.3
Так как в случае высокодобротных элементов, сопротивление контура на резонансной частоте может превышать значение в сотню
килоом, для корректного измерения добротности, входные импедансы измерителя ВЧ напряжений, либо осциллографа должны превышать
это значение как минимум на порядок.
Все наши рассуждения и формулы корректны для ненагруженных параллельных колебательных контуров, то есть для случаев, когда на выходе
отсутствует реальная нагрузка.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность.
Эквивалентная добротность Q параллельного колебательного контура с учётом этих потерь вычисляется по следующей формуле:
Q = Q0
x Rш/(Rш+Rо) , где
Q0 – добротность ненагруженного контура,
Rш – шунтирующее сопротивление, равное R(источника) ll R(нагрузки),
Rо – эквивалентное сопротивление ненагруженного контура, равное сопротивлению контура на резонансной частоте,
значение которого можно посчитать на той же странице ссылка на страницу во 2-ой таблице.
А на следующей странице порассуждаем на тему: что надо сделать, чтобы намотать катушку с максимально-возможной добротностью.
![]()
Методы определения добротности
Пользуясь
определением добротности, можно показать,
что
![]() ,
,
(9)
RП
= r + R + RL,
где RП
– полное сопротивление цепи; r
– внутреннее сопротивление источника
тока; R
– сопротивление, включенное в контур;
RL
– активное сопротивление катушки
индуктивности.
1. Расчет
теоретического значения добротности.
Добротность контура Qтеор
можно рассчитать по формуле (9), зная
параметры электрической цепи RП,
L
и C.
2. Определение
добротности по измерениям резонансного
напряжения U0
рез
и амплитуды вынуждающей ЭДС 0.
Соотношение (8) при малых коэффициентах
затухания принимает вид
![]() ,
,
откуда
![]() .
.
(10)
3. Определение
добротности по ширине резонансной
кривой.
Шириной резонансной кривой называется
разность частот, при которых достигается
эффективное значение резонансного
напряжения на конденсаторе, равное (см.
рис. 3)
![]() .
.
Разность этих
частот
= 2
– 1
является
полосой пропускания контура.
Энергия, запасенная
в контуре при резонансе, на границах
полосы пропускания уменьшается в два
раза.
Пользуясь
соотношениями (9) и (10) и преобразуя
уравнение (5), получаем, что с достаточной
степенью точности
![]() .
.
(11)
Таким
образом, зная
и рез,
можно вычислить добротность контура.
Расчет добротности
этим методом производится с помощью
полученной экспериментально резонансной
кривой в координатах U0
, .
По ней определяются для
![]() значения
значения
1
и 2
слева и справа от рез.
Вместо рез
и циклических частот 1
и 2
используются соответствующие частоты
генератора
![]() .
.
(12)
Метод измерения и описание аппаратуры
Для выполнения
работы используется простейший
колебательный контур из последовательно
соединенных катушки индуктивности L,
конденсатора C
и сопротивления R.
Резонансные кривые снимают при различных
сопротивлениях, включенных в контур.
Наблюдение за изменением амплитуды
колебаний на конденсаторе производится
с помощью электронного осциллографа.
Для этого сигнал с конденсатора подается
на вход осциллографа, и при изменении
частоты генератора измеряется амплитуда
напряжения. При этом диапазон частот
выбирается достаточно широким в обе
стороны по отношению к резонансной
частоте. Резонансная частота соответствует
наибольшей амплитуде измеряемого
напряжения при заданном сопротивлении
контура. Определение добротности контура
производится двумя из вышеописанных
способов: по ширине резонансной кривой
и по отношению резонансного напряжения
к амплитуде вынуждающей ЭДС. Полученные
результаты позволяют вычислить омическое
сопротивление контура и оценить значение
внутреннего сопротивления генератора.
Порядок выполнения работы
-
Включите генератор
синусоидальных колебаний и электронный
осциллограф и соберите схему для
измерений в соответствии с указаниями
на стенде. -
Рассчитайте
собственную частоту контура по формуле
![]() .
.
Параметры L,
C,
RL,
r
контура
даны на стенде. Значения L,
C
и f0
запишите в
табл. 1.
-
Определите по
осциллографу амплитуды вынужденных
колебаний напряжения U0,
снимаемого с конденсатора в делениях
масштабной сетки на экране осциллографа,
при фиксированных значениях частоты
F
генератора в выбранном диапазоне частот
при R1.
Полученные данные занесите в табл. 1. -
Повторите опыт
(пункт 3) при другом сопротивлении R2,
включенном в контур. -
Не изменяя
настройки генератора определите
амплитуду колебаний ЭДС генератора,
соответствующую резонансной частоте,
полученной экспериментально в п. 3,4.
Для этого установите на генераторе
резонансную частоту, выход генератора
подключите непосредственно к входу
электронного осциллографа с помощью
переключателя на стенде, и зафиксируйте
амплитуду сигнала 0.
Результат занесите в табл. 1 и табл. 2. -
По данным табл.
1 постройте резонансные кривые при
различных сопротивлениях контура R1
и R2. -
На каждой
резонансной кривой отметьте уровень,
соответствующий 0,7U0
рез.
Таблица 1
|
№ |
Частота |
U0, |
|
|
п/п |
F, |
R1 |
R2 |
|
1 2 … 11 |
С
= … Ф; f0
= … КГц;
L
= … Гн; 0
= … В.
Соседние файлы в папке 2000
- #
09.06.201525.6 Кб260.DOC
- #
09.06.2015182.78 Кб2701.DOC
- #
09.06.2015304.64 Кб2602.DOC
- #
09.06.2015189.95 Кб2603.DOC
- #
09.06.2015293.89 Кб4604.DOC

A damped oscillation. A low Q factor – about 5 here – means the oscillation dies out rapidly.
In physics and engineering, the quality factor or Q factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation.[1] Q factor is alternatively defined as the ratio of a resonator’s centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results.[2] Higher Q indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high Q, while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer.
Explanation[edit]
The Q factor is a parameter that describes the resonance behavior of an underdamped harmonic oscillator (resonator). Sinusoidally driven resonators having higher Q factors resonate with greater amplitudes (at the resonant frequency) but have a smaller range of frequencies around that frequency for which they resonate; the range of frequencies for which the oscillator resonates is called the bandwidth. Thus, a high-Q tuned circuit in a radio receiver would be more difficult to tune, but would have more selectivity; it would do a better job of filtering out signals from other stations that lie nearby on the spectrum. High-Q oscillators oscillate with a smaller range of frequencies and are more stable.
The quality factor of oscillators varies substantially from system to system, depending on their construction. Systems for which damping is important (such as dampers keeping a door from slamming shut) have Q near 1⁄2. Clocks, lasers, and other resonating systems that need either strong resonance or high frequency stability have high quality factors. Tuning forks have quality factors around 1000. The quality factor of atomic clocks, superconducting RF cavities used in accelerators, and some high-Q lasers can reach as high as 1011[3] and higher.[4]
There are many alternative quantities used by physicists and engineers to describe how damped an oscillator is. Important examples include: the damping ratio, relative bandwidth, linewidth and bandwidth measured in octaves.
The concept of Q originated with K. S. Johnson of Western Electric Company’s Engineering Department while evaluating the quality of coils (inductors). His choice of the symbol Q was only because, at the time, all other letters of the alphabet were taken. The term was not intended as an abbreviation for “quality” or “quality factor”, although these terms have grown to be associated with it.[5][6][7]
Definition[edit]
The definition of Q since its first use in 1914 has been generalized to apply to coils and condensers, resonant circuits, resonant devices, resonant transmission lines, cavity resonators,[5] and has expanded beyond the electronics field to apply to dynamical systems in general: mechanical and acoustic resonators, material Q and quantum systems such as spectral lines and particle resonances.
Bandwidth definition[edit]
In the context of resonators, there are two common definitions for Q, which aren’t exactly equivalent. They become approximately equivalent as Q becomes larger, meaning the resonator becomes less damped. One of these definitions is the frequency-to-bandwidth ratio of the resonator:[5]
where fr is the resonant frequency, Δf is the resonance width or full width at half maximum (FWHM) i.e. the bandwidth over which the power of vibration is greater than half the power at the resonant frequency, ωr = 2πfr is the angular resonant frequency, and Δω is the angular half-power bandwidth.
Under this definition, Q is the reciprocal of fractional bandwidth.
Stored energy definition[edit]
The other common nearly equivalent definition for Q is the ratio of the energy stored in the oscillating resonator to the energy dissipated per cycle by damping processes:[8][9][5]
The factor 2π makes Q expressible in simpler terms, involving only the coefficients of the second-order differential equation describing most resonant systems, electrical or mechanical. In electrical systems, the stored energy is the sum of energies stored in lossless inductors and capacitors; the lost energy is the sum of the energies dissipated in resistors per cycle. In mechanical systems, the stored energy is the sum of the potential and kinetic energies at some point in time; the lost energy is the work done by an external force, per cycle, to maintain amplitude.
More generally and in the context of reactive component specification (especially inductors), the frequency-dependent definition of Q is used:[8][10][failed verification – see discussion][9]
where ω is the angular frequency at which the stored energy and power loss are measured. This definition is consistent with its usage in describing circuits with a single reactive element (capacitor or inductor), where it can be shown to be equal to the ratio of reactive power to real power. (See Individual reactive components.)
Q factor and damping[edit]
The Q factor determines the qualitative behavior of simple damped oscillators. (For mathematical details about these systems and their behavior see harmonic oscillator and linear time invariant (LTI) system.)
- A system with low quality factor (Q < 1⁄2) is said to be overdamped. Such a system doesn’t oscillate at all, but when displaced from its equilibrium steady-state output it returns to it by exponential decay, approaching the steady state value asymptotically. It has an impulse response that is the sum of two decaying exponential functions with different rates of decay. As the quality factor decreases the slower decay mode becomes stronger relative to the faster mode and dominates the system’s response resulting in a slower system. A second-order low-pass filter with a very low quality factor has a nearly first-order step response; the system’s output responds to a step input by slowly rising toward an asymptote.
- A system with high quality factor (Q > 1⁄2) is said to be underdamped. Underdamped systems combine oscillation at a specific frequency with a decay of the amplitude of the signal. Underdamped systems with a low quality factor (a little above Q = 1⁄2) may oscillate only once or a few times before dying out. As the quality factor increases, the relative amount of damping decreases. A high-quality bell rings with a single pure tone for a very long time after being struck. A purely oscillatory system, such as a bell that rings forever, has an infinite quality factor. More generally, the output of a second-order low-pass filter with a very high quality factor responds to a step input by quickly rising above, oscillating around, and eventually converging to a steady-state value.
- A system with an intermediate quality factor (Q = 1⁄2) is said to be critically damped. Like an overdamped system, the output does not oscillate, and does not overshoot its steady-state output (i.e., it approaches a steady-state asymptote). Like an underdamped response, the output of such a system responds quickly to a unit step input. Critical damping results in the fastest response (approach to the final value) possible without overshoot. Real system specifications usually allow some overshoot for a faster initial response or require a slower initial response to provide a safety margin against overshoot.
In negative feedback systems, the dominant closed-loop response is often well-modeled by a second-order system. The phase margin of the open-loop system sets the quality factor Q of the closed-loop system; as the phase margin decreases, the approximate second-order closed-loop system is made more oscillatory (i.e., has a higher quality factor).
Some examples[edit]
- A unity-gain Sallen–Key lowpass filter topology with equal capacitors and equal resistors is critically damped (i.e., Q = 1⁄2).
- A second-order Bessel filter (i.e., continuous-time filter with flattest group delay) has an underdamped Q = 1⁄√3.
- A second-order Butterworth filter (i.e., continuous-time filter with the flattest passband frequency response) has an underdamped Q = 1⁄√2.[11]
- A pendulum’s Q-factor is:
, where M is the mass of the bob, ω = 2π/T is the pendulum’s radian frequency of oscillation, and Γ is the frictional damping force on the pendulum per unit velocity.
- The design of a high-energy (near THz) gyrotron considers both diffractive Q-factor,
as a function of resonator length (L) and wavelength (
), and ohmic Q-factor (
–modes)
,
where
is the cavity wall radius,
is the skin depth of the cavity wall,
is the eigenvalue scalar (m is azimuth index, p is radial index; in this application, skin depth is
)[12]
- In medical ultrasonography, a transducer with a high Q-factor is suitable for doppler ultrasonography because of its long ring-down time, where it can measure the velocities of blood flow. Meanwhile, a transducer with a low Q-factor has a short ring-down time and is suitable for organ imaging because it can receive a broad range of reflected echoes from bodily organs.[13]
Physical interpretation[edit]
Physically speaking, Q is approximately the ratio of the stored energy to the energy dissipated over one radian of the oscillation; or nearly equivalently, at high enough Q values, 2π times the ratio of the total energy stored and the energy lost in a single cycle.[14]
It is a dimensionless parameter that compares the exponential time constant τ for decay of an oscillating physical system’s amplitude to its oscillation period. Equivalently, it compares the frequency at which a system oscillates to the rate at which it dissipates its energy. More precisely, the frequency and period used should be based on the system’s natural frequency, which at low Q values is somewhat higher than the oscillation frequency as measured by zero crossings.
Equivalently (for large values of Q), the Q factor is approximately the number of oscillations required for a freely oscillating system’s energy to fall off to e−2π, or about 1⁄535 or 0.2%, of its original energy.[15] This means the amplitude falls off to approximately e−π or 4% of its original amplitude.[16]
The width (bandwidth) of the resonance is given by (approximately):
where fN is the natural frequency, and Δf, the bandwidth, is the width of the range of frequencies for which the energy is at least half its peak value.
The resonant frequency is often expressed in natural units (radians per second), rather than using the fN in hertz, as
The factors Q, damping ratio ζ, natural frequency ωN, attenuation rate α, and exponential time constant τ are related such that:[17][page needed]
and the damping ratio can be expressed as:
The envelope of oscillation decays proportional to e−αt or e−t/τ, where α and τ can be expressed as:
and
The energy of oscillation, or the power dissipation, decays twice as fast, that is, as the square of the amplitude, as e−2αt or e−2t/τ.
For a two-pole lowpass filter, the transfer function of the filter is[17]
For this system, when Q > 1⁄2 (i.e., when the system is underdamped), it has two complex conjugate poles that each have a real part of −α. That is, the attenuation parameter α represents the rate of exponential decay of the oscillations (that is, of the output after an impulse) into the system. A higher quality factor implies a lower attenuation rate, and so high-Q systems oscillate for many cycles. For example, high-quality bells have an approximately pure sinusoidal tone for a long time after being struck by a hammer.
| Filter type (2nd order) | Transfer function[18] |
|---|---|
| Lowpass | 
|
| Bandpass | 
|
| Notch (bandstop) | 
|
| Highpass | 
|
Electrical systems[edit]

A graph of a filter’s gain magnitude, illustrating the concept of −3 dB at a voltage gain of 0.707 or half-power bandwidth. The frequency axis of this symbolic diagram can be linear or logarithmically scaled.
For an electrically resonant system, the Q factor represents the effect of electrical resistance and, for electromechanical resonators such as quartz crystals, mechanical friction.
Relationship between Q and bandwidth[edit]
The 2-sided bandwidth relative to a resonant frequency of F0 Hz is F0/Q.
For example, an antenna tuned to have a Q value of 10 and a centre frequency of 100 kHz would have a 3 dB bandwidth of 10 kHz.
In audio, bandwidth is often expressed in terms of octaves. Then the relationship between Q and bandwidth is
where BW is the bandwidth in octaves.[19]
RLC circuits[edit]
In an ideal series RLC circuit, and in a tuned radio frequency receiver (TRF) the Q factor is:[20]
where R, L and C are the resistance, inductance and capacitance of the tuned circuit, respectively. The larger the series resistance, the lower the circuit Q.
For a parallel RLC circuit, the Q factor is the inverse of the series case:[21][20]
[22]
Consider a circuit where R, L and C are all in parallel. The lower the parallel resistance, the more effect it will have in damping the circuit and thus the lower the Q. This is useful in filter design to determine the bandwidth.
In a parallel LC circuit where the main loss is the resistance of the inductor, R, in series with the inductance, L, Q is as in the series circuit. This is a common circumstance for resonators, where limiting the resistance of the inductor to improve Q and narrow the bandwidth is the desired result.
Individual reactive components[edit]
The Q of an individual reactive component depends on the frequency at which it is evaluated, which is typically the resonant frequency of the circuit that it is used in. The Q of an inductor with a series loss resistance is the Q of a resonant circuit using that inductor (including its series loss) and a perfect capacitor.[23]
where:
- ω0 is the resonance frequency in radians per second,
- L is the inductance,
- XL is the inductive reactance, and
- RL is the series resistance of the inductor.
The Q of a capacitor with a series loss resistance is the same as the Q of a resonant circuit using that capacitor with a perfect inductor:[23]
where:
- ω0 is the resonance frequency in radians per second,
- C is the capacitance,
- XC is the capacitive reactance, and
- RC is the series resistance of the capacitor.
In general, the Q of a resonator involving a series combination of a capacitor and an inductor can be determined from the Q values of the components, whether their losses come from series resistance or otherwise:[23]
Mechanical systems[edit]
For a single damped mass-spring system, the Q factor represents the effect of simplified viscous damping or drag, where the damping force or drag force is proportional to velocity. The formula for the Q factor is:
where M is the mass, k is the spring constant, and D is the damping coefficient, defined by the equation Fdamping = −Dv, where v is the velocity.[24]
Acoustical systems[edit]
The Q of a musical instrument is critical; an excessively high Q in a resonator will not evenly amplify the multiple frequencies an instrument produces. For this reason, string instruments often have bodies with complex shapes, so that they produce a wide range of frequencies fairly evenly.
The Q of a brass instrument or wind instrument needs to be high enough to pick one frequency out of the broader-spectrum buzzing of the lips or reed.
By contrast, a vuvuzela is made of flexible plastic, and therefore has a very low Q for a brass instrument, giving it a muddy, breathy tone. Instruments made of stiffer plastic, brass, or wood have higher-Q. An excessively high Q can make it harder to hit a note. Q in an instrument may vary across frequencies, but this may not be desirable.
Helmholtz resonators have a very high Q, as they are designed for picking out a very narrow range of frequencies.
Optical systems[edit]
In optics, the Q factor of a resonant cavity is given by
where fo is the resonant frequency, E is the stored energy in the cavity, and P = −dE/dt is the power dissipated. The optical Q is equal to the ratio of the resonant frequency to the bandwidth of the cavity resonance. The average lifetime of a resonant photon in the cavity is proportional to the cavity’s Q. If the Q factor of a laser’s cavity is abruptly changed from a low value to a high one, the laser will emit a pulse of light that is much more intense than the laser’s normal continuous output. This technique is known as Q-switching. Q factor is of particular importance in plasmonics, where loss is linked to the damping of the surface plasmon resonance.[25] While loss is normally considered a hindrance in the development of plasmonic devices, it is possible to leverage this property to present new enhanced functionalities.[26]
See also[edit]
- Acoustic resonance
- Attenuation
- Chu–Harrington limit
- Piezoelectric material properties
- Phase margin
- Q meter
- Q multiplier
- Dissipation factor
References[edit]
- ^ Hickman, Ian (2013). Analog Electronics: Analog Circuitry Explained. Newnes. p. 42. ISBN 9781483162287.
- ^ Tooley, Michael H. (2006). Electronic circuits: fundamentals and applications. Newnes. pp. 77–78. ISBN 978-0-7506-6923-8. Archived from the original on 2016-12-01.
- ^
Encyclopedia of Laser Physics and Technology: Q factor Archived 2009-02-24 at the Wayback Machine
- ^
Time and Frequency from A to Z: Q to Ra Archived 2008-05-04 at the Wayback Machine
- ^ a b c d
Green, Estill I. (October 1955). “The Story of Q” (PDF). American Scientist. 43: 584–594. Archived (PDF) from the original on 2012-12-03. Retrieved 2012-11-21. - ^ B. Jeffreys, Q.Jl R. astr. Soc. (1985) 26, 51–52
- ^ Paschotta, Rüdiger (2008). Encyclopedia of Laser Physics and Technology, Vol. 1: A-M. Wiley-VCH. p. 580. ISBN 978-3527408283. Archived from the original on 2018-05-11.
- ^ a b Slyusar V. I. 60 Years of Electrically Small Antennas Theory.//Proceedings of the 6-th International Conference on Antenna Theory and Techniques, 17–21 September 2007, Sevastopol, Ukraine. – Pp. 116 – 118. “ANTENNA THEORY AND TECHNIQUES” (PDF). Archived (PDF) from the original on 2017-08-28. Retrieved 2017-09-02.
- ^ a b U.A.Bakshi, A. V. Bakshi (2006). Network Analysis. Technical Publications. p. 228. ISBN 9788189411237.
- ^ James W. Nilsson (1989). Electric Circuits. ISBN 0-201-17288-7.
- ^ Sabah, Nassir H. (2017). Circuit Analysis with PSpice: A Simplified Approach. CRC Press. p. 446. ISBN 9781315402215.
- ^ “Near THz Gyrotron: Theory, Design, and Applications” (PDF). The Institute for Research in Electronics and Applied Physics. University of Maryland. Retrieved 5 January 2021.
- ^ Curry, TS; Dowdey, JE; Murry, RC (1990). Christensen’s Physics of Diagnostic Radiology. Lippincott Williams & Wilkins. p. 331. ISBN 9780812113105. Retrieved 22 January 2023.
- ^
Jackson, R. (2004). Novel Sensors and Sensing. Bristol: Institute of Physics Pub. p. 28. ISBN 0-7503-0989-X. - ^ Benjamin Crowell (2006). “Light and Matter”. Archived from the original on 2011-05-19., Ch. 18
- ^ Anant., Agarwal (2005). Foundations of analog & digital electronic circuits. Lang, Jeffrey (Jeffrey H.). Amsterdam: Elsevier. p. 647. ISBN 9781558607354. OCLC 60245509.
- ^ a b Siebert, William McC. Circuits, Signals, and Systems. MIT Press.
- ^ “Analog Dialogue Technical Journal – Analog Devices” (PDF). www.analog.com. Archived (PDF) from the original on 2016-08-04.
- ^ Dennis Bohn, Rane (January 2008). “Bandwidth in Octaves Versus Q in Bandpass Filters”. www.rane.com. Retrieved 2019-11-20.
- ^ a b U.A.Bakshi; A.V.Bakshi (2008). Electric Circuits. Technical Publications. pp. 2–79. ISBN 9788184314526.
- ^ “Complete Response I – Constant Input”. fourier.eng.hmc.edu. Archived from the original on 2012-01-10.
- ^ Frequency Response: Resonance, Bandwidth, Q Factor Archived 2014-12-06 at the Wayback Machine (PDF)
- ^ a b c
Di Paolo, Franco (2000). Networks and Devices Using Planar Transmission Lines. CRC Press. pp. 490–491. ISBN 9780849318351. Archived from the original on 2018-05-11. - ^ Methods of Experimental Physics – Lecture 5: Fourier Transforms and Differential Equations Archived 2012-03-19 at the Wayback Machine (PDF)
- ^ Tavakoli, Mehdi; Jalili, Yousef Seyed; Elahi, Seyed Mohammad (2019-04-28). “Rayleigh-Wood anomaly approximation with FDTD simulation of plasmonic gold nanohole array for determination of optimum extraordinary optical transmission characteristics”. Superlattices and Microstructures. 130: 454–471. Bibcode:2019SuMi..130..454T. doi:10.1016/j.spmi.2019.04.035. S2CID 150365680.
- ^ Chen, Gang; Mahan, Gerald; Meroueh, Laureen; Huang, Yi; Tsurimaki, Yoichiro; Tong, Jonathan K.; Ni, George; Zeng, Lingping; Cooper, Thomas Alan (2017-12-31). “Losses in plasmonics: from mitigating energy dissipation to embracing loss-enabled functionalities”. Advances in Optics and Photonics. 9 (4): 775–827. Bibcode:2017AdOP….9..775B. doi:10.1364/AOP.9.000775. ISSN 1943-8206.
Further reading[edit]
- Agarwal, Anant; Lang, Jeffrey (2005). Foundations of Analog and Digital Electronic Circuits. Morgan Kaufmann. ISBN 1-55860-735-8.
External links[edit]
- Calculating the cut-off frequencies when center frequency and Q factor is given
- Explanation of Q factor in radio tuning circuits



















