1.21.
3АТУХАЮЩИЕ, ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Дифференциальное
уравнение затухающих колебаний и его
решение. Коэффициент затухания.
Логарифмический декремент
затухания. Добротность
колебательной
системы. Апериодический
процесс. Дифференциальное уравнение
вынужденных колебаний и его решение.
Амплитуда
и фаза вынужденных колебаний. Процесс
установления колебаний. Случай резонанса.
Автоколебания.
Затуханием
колебаний называется постепенное
уменьшение амплитуды колебаний с
течением времени, обусловленное потерей
энергии колебательной системой.
Собственные
колебания без затухания – это идеализация.
Причины затухания могут быть разные. В
механической системе к затуханию
колебаний приводит наличие трения.
Когда израсходуется вся энергия,
запасенная в колебательной системе,
колебания прекратятся. Поэтому амплитуда
затухающих
колебаний
уменьшается,
пока не станет равной нулю.
Затухающие колебания,
как и собственные, в системах, разных
по своей природе, можно рассматривать
с единой точки зрения – общих признаков.
Однако, такие характеристики, как
амплитуда и период, требуют переопределения,
а другие – дополнения и уточнения по
сравнению с такими же признаками для
собственных незатухающих колебаний.
Общие признаки и понятия затухающих
колебаний следующие:
-
Дифференциальное
уравнение должно быть получено с учетом
убывания в процессе колебаний
колебательной энергии. -
Уравнение колебаний
– решение дифференциального уравнения. -
Амплитуда затухающих
колебаний зависит от времени. -
Частота и период
зависят от степени затухания колебаний. -
Фаза и начальная
фаза имеют тот же смысл, что и для
незатухающих колебаний.
Механические
затухающие колебания.
Механическая
система:
пружинный маятник с учетом сил трения.
Силы,
действующие на маятник:
Упругая
сила.
![]() ,
,
где k
– коэффициент жесткости пружины, х –
смещение маятника от положения равновесия.
Сила
сопротивления.
Рассмотрим силу сопротивления,
пропорциональную скорости v
движения (такая зависимость характерна
для большого класса сил сопротивления):
![]() .
.
Знак “минус” показывает, что направление
силы сопротивления противоположно
направлению скорости движения тела.
Коэффициент сопротивления r
численно равен силе сопротивления,
возникающей при единичной скорости
движения тела:
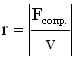
Закон
движения
пружинного
маятника – это второй закон Ньютона:
ma
= Fупр.
+ Fсопр.
Учитывая,
что
![]() и
и
 ,
,
запишем второй закон Ньютона в виде:
 . (21.1)
. (21.1)
Разделив
все члены уравнения на m,
перенеся их все в правую часть, получим
дифференциальное
уравнение
затухающих колебаний:

Обозначим
![]() ,
,
где β
– коэффициент
затухания,
![]() ,
,
где ω0
– частота незатухающих свободных
колебаний в отсутствии потерь энергии
в колебательной системе.
В новых обозначениях
дифференциальное уравнение затухающих
колебаний имеет вид:
 .
.
(21.2)
Это линейное
дифференциальное уравнение второго
порядка.
Это
линейное дифференциальное уравнение
решается заменой переменных. Представим
функцию х, зависящую от времени t,
в виде:
![]() .
.
Найдем
первую и вторую производную этой функции
от времени, учитывая, что функция z
также является функцией времени:
![]() ,
,
 .
.
Подставим выражения
в дифференциальное уравнение:
 .
.
Приведем
подобные члены в уравнении и сократим
каждый член на
![]() ,
,
получим уравнение:
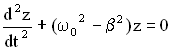 .
.
Обозначим
величину
![]() .
.
Решением
уравнения
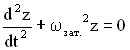 являются
являются
функции
![]() ,
,
![]() .
.
Возвращаясь к
переменной х, получим формулы уравнений
затухающих колебаний:
![]()
![]() .
.
Таким
образом,
уравнение затухающих колебаний есть
решение дифференциального уравнения
(21.2):
![]()
![]()
(21.3)
Частота
затухающих колебаний:
![]() (физический
(физический
смысл имеет только вещественный корень,
поэтому
![]() ).
).
Период
затухающих колебаний:
 (21.5)
(21.5)
Смысл,
который вкладывался в понятие периода
для незатухающих колебаний, не подходит
для затухающих колебаний, так как
колебательная система никогда не
возвращается в исходное состояние из-за
потерь колебательной энергии. При
наличии трения колебания идут медленнее:
![]() .
.
Периодом
затухающих колебаний
называется минимальный промежуток
времени, за который система проходит
дважды положение равновесия в одном
направлении.
Для механической
системы пружинного маятника имеем:
 ,
,
 .
.
Амплитуда
затухающих колебаний:
![]() ,
,
для пружинного маятника
![]() .
.
Амплитуда
затухающих колебаний – величина не
постоянная, а изменяющаяся со временем
тем быстрее, чем больше коэффициент β.
Поэтому определение для амплитуды,
данное ранее для незатухающих свободных
колебаний, для затухающих колебаний
надо изменить.
При
небольших затуханиях амплитудой
затухающих колебаний
называется
наибольшее отклонение от положения
равновесия за период.
Графики
зависимости
смещения от времени
![]() и
и
амплитуды от времени
![]() представлены
представлены
на Рисунках 21.1 и 21.2.

Рисунок
21.1 – Зависимость смещения от времени
для затухающих колебаний.

Рисунок
21.2 – Зависимости амплитуды от времени
для затухающих колебаний
Характеристики
затухающих колебаний.
1.
Коэффициент затухания
β.
Изменение амплитуды
затухающих колебаний происходит по
экспоненциальному закону:
![]() .
.
Пусть за
время τ
амплитуда колебаний уменьшится в “e
” раз (“е” – основание натурального
логарифма, е ≈ 2,718). Тогда, с одной стороны,
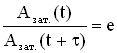 ,
,
а с другой стороны, расписав амплитуды
Азат.(t)
и Азат.(t+τ),
имеем
 .
.
Из этих соотношений следует βτ
= 1, отсюда
![]() .
.
Промежуток
времени τ,
за который амплитуда уменьшается в “е”
раз, называется временем релаксации.
Коэффициент
затухания β
– величина, обратно пропорциональная
времени релаксации.
2.
Логарифмический
декремент затухания δ
–
физическая величина, численно равная
натуральному логарифму отношения двух
последовательных амплитуд, отстоящих
по времени на период .


Если
затухание невелико, т.е. величина β
мала, то амплитуда незначительно
изменяется за период, и логарифмический
декремент можно определить так:
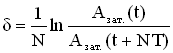 ,
,
где
Азат.(t)
и Азат.(t+NT)
– амплитуды колебаний в момент времени
е и через N
периодов, т.е.в момент времени (t
+ NT).
3.
Добротность Q
колебательной системы
– безразмерная физическая величина,
равная произведению величины (2π)
νа
отношение энергии W(t)
системы в произвольный момент времени
к убыли энергии за один период затухающих
колебаний:
 .
.
Так как энергия
пропорциональна квадрату амплитуды,
то
 .
.
При малых
значениях логарифмического декремента
δ
добротность колебательной системы
равна
![]() ,
,
где Ne
– число колебаний, за которое амплитуда
уменьшается в “е” раз.
Так,
добротность пружинного маятника –
 .Чем
.Чем
больше добротность колебательной
системы, тем меньше затухание, тем дольше
будет длиться периодический процесс в
такой системе. Добротность
колебательной системы – безразмерная
величина, которая характеризует
диссипацию энергии во времени.
4. При
увеличении коэффициента β,
частота затухающих колебаний уменьшается,
а период увеличивается. При ω0
= β
частота затухающих колебаний становится
равной нулю ωзат.
= 0, а Тзат.
=
∞. При этом колебания теряют периодический
характер и называются апериодическими.
При ω0
= β
параметры системы, ответственные за
убывание колебательной энергии, принимают
значения, называемые критическими.
Для пружинного маятника условие ω0
= β
запишется так: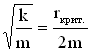 ,
,
откуда найдем величину критического
коэффициента сопротивления:
![]() .
.

Рис. 21.3.
Зависимсть амплитуды апериодических
колебаний от времени
Вынужденные
колебания.
Все реальные колебания
являются затухающими. Чтобы реальные
колебания происходили достаточно долго
нужно периодически пополнять энергию
колебательной системы, действуя на нее
внешней периодически изменяющейся
силой
Рассмотрим
явление колебаний, если внешняя
(вынуждающая)
сила изменяется в зависимости от времени
по гармоническому закону. При этом в
системах возникнут колебания, характер
которых в той или иной мере повторит
характер вынуждающей силы. Такие
колебания называются вынужденными.
Общие признаки
вынужденных механических колебаний.
1. Рассмотрим
вынужденные механические колебаний
пружинного маятника, на который действует
внешняя (вынуждающая)
периодическая сила
![]() .
.
Силы, которые действуют на маятник,
однажды выведенный из положения
равновесия, развиваются в самой
колебательной системе. Это сила упругости
![]() и
и
сила сопротивления
![]() .
.
Закон
движения
(второй закон Ньютона) запишется следующим
образом:
 (21.6)
(21.6)
Разделим
обе части уравнения на m,
учтем, что
![]() ,
,
и получим дифференциальное
уравнение
вынужденных
колебаний:

Обозначим
![]() (β
(β
– коэффициент
затухания),
![]() (ω0
(ω0
– частота незатухающих свободных
колебаний),
![]() сила,
сила,
действующая на единицу массы. В этих
обозначениях дифференциальное
уравнение
вынужденных колебаний примет вид:
 (21.7)
(21.7)
Это дифференциальное
уравнение второго порядка с правой
частью, отличной от нуля. Решение такого
уравнения есть сумма двух решений
![]() .
.
![]() –
–
общее
решение однородного дифференциального
уравнения, т.е. дифференциального
уравнения без правой части, когда она
равна нулю. Такое решение нам известно
– это уравнение затухающих колебаний,
записанное с точностью до постоянной,
значение которой определяется начальными
условиями колебательной системы:
![]() ,
,
где
![]() .
.
Мы обсуждали ранее,
что решение может быть записано через
функции синуса.
Если
рассматривать процесс колебаний маятника
через достаточно большой промежуток
времени Δt
после включения вынуждающей силы
(Рисунок 21.2), то затухающие колебания в
системе практически прекратятся. И
тогда решением дифференциального
уравнения с правой частью будет решение
![]() .
.
Решение
![]() –
–
это частное решение неоднородного
дифференциального уравнения, т.е.
уравнения с правой частью. Из теории
дифференциальных уравнений известно,
что при правой части, изменяющейся по
гармоническому закону, решение
![]() будет
будет
гармонической функцией (sin
или cos)
с частотой изменения, соответствующей
частоте Ω
изменения правой части:
![]() , (21.8)
, (21.8)
где Аампл.
– амплитуда вынужденных колебаний, φ0
–сдвиг
фаз,
т.е. разность фаз между фазой вынуждающей
силы и фазой вынужденных колебаний. И
амплитуда Аампл.,
и сдвиг фаз φ0
зависят от параметров системы (β,
ω0)
и от частоты вынуждающей силы Ω.
Период
вынужденных колебаний равен
![]() (21.9)
(21.9)
График вынужденных
колебаний на Рисунке 4.1.

Рис.21.3. График
вынужденных колебаний
Установившиеся
вынужденные колебания являются так же
гармоническими.
Зависимости
амплитуды вынужденных колебаний и
сдвига фаз от частоты внешнего воздействия.
Резонанс.
1. Вернемся к
механической системе пружинного
маятника, на который действует внешняя
сила, изменяющаяся по гармоническому
закону. Для такой системы дифференциальное
уравнение и его решение соответственно
имеют вид:
 ,
,
![]() .
.
Проанализируем
зависимость амплитуды колебаний и
сдвига фаз от частоты внешней вынуждающей
силы, для этого найдем первую и вторую
производную от х и подставим в
дифференциальное уравнение.
![]() ,
,
 ,
,

Воспользуемся
методом векторной диаграммы. Из уравнения
видно, что сумма трех колебаний в левой
части уравнения (Рисунок 4.1) должна быть
равна колебанию в правой части. Векторная
диаграмма выполнена для произвольного
момента времени t.
Из нее можно определить
![]() .
.

Рисунок
21.4.
 , (21.10)
, (21.10)
 . (21.11)
. (21.11)
Учитывая
значение
![]() ,
,
![]() ,
,![]() ,
,
получим формулы для φ0
и Аампл.
механической системы:
 ,
,
 .
.
2. Исследуем
зависимость амплитуды вынужденных
колебаний от частоты вынуждающей силы
и величины силы сопротивления в
колеблющейся механической системе, по
этим данным построим график
![]() .
.
Результаты исследования отражены в
Рисунке 21.5, по ним видно, что при некоторой
частоте вынуждающей силы
![]() амплитуда
амплитуда
колебаний резко возрастает. И это
возрастание тем больше, чем меньше
коэффициент затухания β.
При
![]() амплитуда
амплитуда
колебаний становится бесконечно большой
![]() .
.
Явление
резкого возрастания амплитуды
вынужденных
колебаний при частоте вынуждающей силы,
равной
![]() ,
,
называется резонансом.
![]() (21.12)
(21.12)
Кривые
на Рисунке 21.5 отражают зависимость
![]() и
и
называются амплитудными
резонансными кривыми.

Рисунок
21.5 – Графики зависимости амплитуды
вынужденных колебаний от частоты
вынуждающей силы.
Амплитуда резогансных
колебаний примет вид:

(21.13)
Вынужденные
колебания – это незатухающие
колебания. Неизбежные потери энергии
на трение компенсируются подводом
энергии от внешнего источника периодически
действующей силы. Существуют системы,
в которых незатухающие колебания
возникают не за счет периодического
внешнего воздействия, а в результате
имеющейся у таких систем способности
самой регулировать поступление энергии
от постоянного источника. Такие системы
называются автоколебательными,
а процесс незатухающих колебаний в
таких системах – автоколебаниями.
В автоколебательной
системе можно выделить три характерных
элемента – колебательная система,
источник энергии и устройство обратной
связи между колебательной системой и
источником. В качестве колебательной
системы может быть использована любая
механическая система, способная совершать
собственные затухающие колебания
(например, маятник настенных часов).
Источником
энергии может служить энергия деформация
пружины или потенциальная энергия груза
в поле тяжести. Устройство обратной
связи представляет собой некоторый
механизм, с помощью которого
автоколебательная система регулирует
поступление энергии от источника. На
рис. 21.6 изображена схема взаимодействия
различных элементов автоколебательной
системы.
|
|
|
Рисунок |
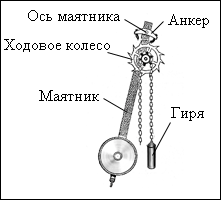
Примером
механической автоколебательной системы
может служить часовой механизм с анкерным
ходом (рис. 21.7.). Ходовое колесо с косыми
зубьями жестко скреплено с зубчатым
барабаном, через который перекинута
цепочка с гирей. На верхнем конце маятника
закреплен анкер (якорек) с двумя
пластинками из твердого материала,
изогнутыми по дуге окружности с центром
на оси маятника. В ручных часах гиря
заменяется пружиной, а маятник –
балансиром – маховичком, скрепленным
со спиральной пружиной.
|
|
|
Рисунок |
Балансир совершает
крутильные колебания вокруг своей оси.
Колебательной системой в часах является
маятник или балансир. Источником энергии
– поднятая вверх гиря или заведенная
пружина. Устройством, с помощью которого
осуществляется обратная связь, является
анкер, позволяющий ходовому колесу
повернуться на один зубец за один
полупериод.
Обратная связь
осуществляется взаимодействием анкера
с ходовым колесом. При каждом колебании
маятника зубец ходового колеса толкает
анкерную вилку в направлении движения
маятника, передавая ему некоторую порцию
энергии, которая компенсирует потери
энергии на трение. Таким образом,
потенциальная энергия гири (или
закрученной пружины) постепенно,
отдельными порциями передается маятнику.
Механические
автоколебательные системы широко
распространены в окружающей нас жизни
и в технике. Автоколебания совершают
паровые машины, двигатели внутреннего
сгорания, электрические звонки, струны
смычковых музыкальных инструментов,
воздушные столбы в трубах духовых
инструментов, голосовые связки при
разговоре или пении и т. д.
13
Соседние файлы в папке физика лекцыи
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R, с емкостью конденсатора C, с катушкой индуктивности L, изображенный на рисунке 1. Колебания, происходящие в нем, – затухающие.
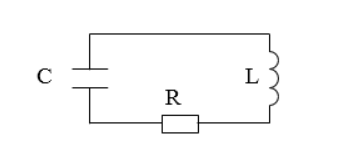
Рисунок 1
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания β. Применив второй закон Ньютона, получим:
ma=-kx-yv,d2xdt2+rmdxdt+kmx=0,ω02=km,β=r2m.
Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ,
Значение a (t) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а Ne – период времени уменьшения амплитуды в e раз.
Для RLC контура применима формула с ω частотой.
При небольшой δ≪1 говорят, что β≪ω0 ω0=1LC – собственная частота, отсюда ω≈ω0.
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :
Q=1RLC=ω0LR, где R, L и C – сопротивление, индуктивность, емкость, а ω0- частота резонанса. Выражение LC называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
Q=RLC=Rω0L.
R является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
Q=ω0WPd=2πf0WPd, называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок 1. Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:
q(t)=q0e(-βt)cosωt+a’0=q0e-βtcos(ωt).
Если t=0, то заряд конденсатора становится равным q0, и ток в цепи отсутствует.
Если R>2LC изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое Rk.
rкр=2LC.
Функция изображается аналогично рисунку 2.
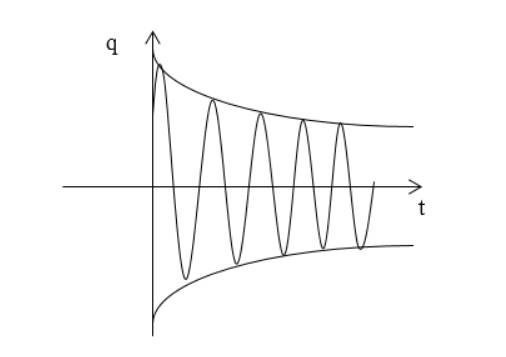
Рисунок 2
Записать закон убывания энергии, запасенной в контуре W (t) при W (t=0)=W0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β, а собственную частоту – ω0.
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в RLC – контуре:
q(t)=q0e(-βt)cosωt+a’0=q0e-βtcos(ωt).
Предположим, что при t=0, a’0=0. Тогда применим выражение
I=dqdt.
Для нахождения I(t):
I(t)=-ω0q0e(-2βt)sin(ωt+α), где tg α=βω.
Очевидно, что электрическая энергия Wq запишется как:
Wq=q22C=q022Ce(-2βt)cos2(ωt)=W0e(-2βt)cos2(ωt).
Тогда значение магнитной энергии контура Wm равняется:
Wm=L2ω02q02e(-2βt)sin2ωt+a=W0e-2βtsin2ωt+a.
Запись полной энергии будет иметь вид:
W=Wq+Wm=W0e(-2βt)(cos2(ωt)+sin2(ωt+a))==W0e(-2βt)1+βω0sin(2ωt+α).
Где sin α=βω0.
Ответ: W (t)=W0e(-2βt)1+βω0sin (2ωt+a).
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W (t), при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
βω0≪1.
Очевидно, выражение энергии, запасенной в контуре, вычислим из
W (t)=W0e(-2βt)1+βω0sin (2ωt+a), предварительно преобразовав до W (t)=W0e(-2βt).
Такое упрощение возможно по причине выполнения условия βω0≪1, sin (2ωt+a)≤1, что означает βω0sin (2ωt+a)≪1.
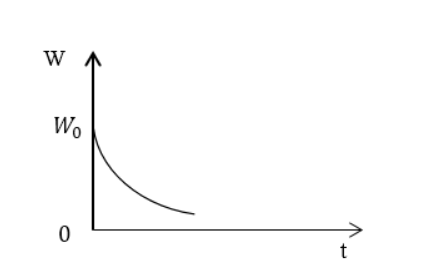
Рисунок 3
Ответ: W (t)=W0e(-2βt). Энергия в контуре убывает по экспоненте.
Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом 
Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.
Теория[править | править код]
Общая формула для добротности любой колебательной системы[1]:
,
где
— резонансная круговая частота колебаний
— резонансная частота колебаний
— энергия, запасённая в колебательной системе
— рассеиваемая мощность.
Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.
Для последовательного колебательного контура в RLC-цепях, в котором все три элемента включены последовательно:
где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно, а 

Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно:

Формулировка частотного отклика или ширины полосы пропускания колебательной системы

ЛАФЧХ колебательных звеньев с разной добротностью
В данном случае R является входным сопротивлением параллельного контура. Однако практически для электрической цепи гораздо проще измерить ток или напряжение, чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды колебаний, ширина полосы частот на АЧХ определяется на высоте 




где δ — логарифмический декремент затухания, равный отношению полуширины резонансной кривой к частоте резонанса, 
Для электрически малых антенн добротность можно определить соотношением[1]:
,
где
— резонансная круговая частота электромагнитных колебаний
— энергия электрического поля, запасённая в антенне
— энергия магнитного поля, запасённая в антенне
— рассеиваемая антенной мощность.
Метрологические аспекты[править | править код]
Для измерения электрической добротности на частотах до десятков и сотен мегагерц применяют измеритель добротности или измеритель иммитанса (косвенным способом), в диапазоне СВЧ применяются специальные методы.
См. также[править | править код]
Измеритель добротности
Примечания[править | править код]
- ↑ 1 2 Слюсар В. И. 60 лет теории электрически малых антенн. Некоторые итоги // Электроника: наука, технология, бизнес. — 2006. — Вып. 7. — С. 10—19.
Литература[править | править код]
- Бидерман В. Л. Теория механических колебаний. — Высшая школа, 1980. — 408 с. — 10 000 экз.
- Горелик Г. С. Колебания и волны. — М.: ГИФМЛ, 1959. — 572 с.
Ссылки[править | править код]
- ГПЭ единицы электрической добротности. ФГУП «СНИИМ». Дата обращения: 12 февраля 2015.
3.1. Механические затухающие колебания
3.2. Электромагнитные затухающие колебания
3.3. Характеристики затухающих колебаний
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:
Упругая сила. ![]() , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
, где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): ![]() . Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
. Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
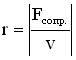 Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Учитывая, что ![]() и
и 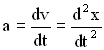 , запишем второй закон Ньютона в виде:
, запишем второй закон Ньютона в виде:
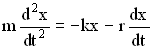 .
.
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
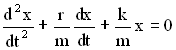
Обозначим ![]() , где β – коэффициент затухания,
, где β – коэффициент затухания, ![]() , где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
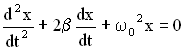 . Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения:
. Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения: ![]()
![]() .
.
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний:
![]() (физический смысл имеет только вещественный корень, поэтому
(физический смысл имеет только вещественный корень, поэтому ![]() ).
).
Период затухающих колебаний: 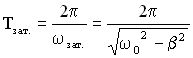 .
.
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: ![]() .
.
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
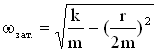 ,
, 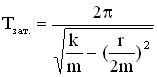 . Амплитуда затухающих колебаний:
. Амплитуда затухающих колебаний: ![]() , для пружинного маятника
, для пружинного маятника ![]() .
.
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Графики зависимости смещения от времени ![]() и амплитуды от времени
и амплитуды от времени ![]() представлены на Рисунках 3.1 и 3.2.
представлены на Рисунках 3.1 и 3.2.
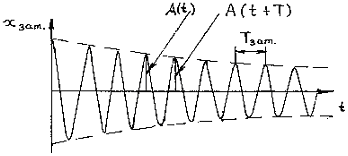
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний

Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
3.2. Электромагнитные затухающие колебания
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
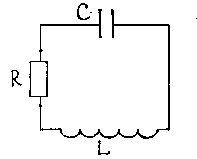
Рисунок 3.3.
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура: ![]()
Падение напряжения:
– на активном сопротивлении: ![]() , где I – сила тока в контуре;
, где I – сила тока в контуре;
– на конденсаторе (С): ![]() , где q – величина заряда на одной из обкладок конденсатора.
, где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: ![]() (закон Фарадея).
(закон Фарадея).
Подставим значения UR, UC, ![]() в уравнение, отражающее закон Кирхгофа, получим:
в уравнение, отражающее закон Кирхгофа, получим:
![]() .
.
Сила тока определяется как производная от заряда ![]() , тогда
, тогда 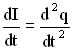 , и дифференциальное уравнение примет вид:
, и дифференциальное уравнение примет вид:
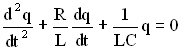 .
.
Обозначим ![]() ,
, ![]() , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
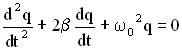
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
![]() или
или
![]() .
.
Амплитуда затухающих колебаний заряда имеет вид:
![]() , где
, где ![]() .
.
Частота затухающих колебаний в LCR – контуре:
 .
.
Период затухающих электромагнитных колебаний:
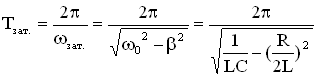 .
.
Возьмем уравнение для заряда в виде ![]() , тогда уравнение для напряжения на обкладках конденсатора можно записать так
, тогда уравнение для напряжения на обкладках конденсатора можно записать так 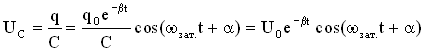 .
.
Величина 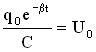 называется амплитудой напряжения на конденсаторе.
называется амплитудой напряжения на конденсаторе.
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение ![]() и векторную диаграмму.
и векторную диаграмму.
Окончательное уравнение для силы тока таково:
![]() ,
,
где 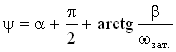 – начальная фаза.
– начальная фаза.
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
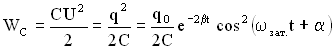
и энергии магнитного поля
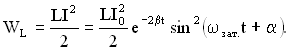
Полная энергия в любой момент времени:
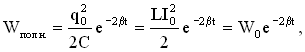
где W0 – полная энергия контура в момент времени t=0.
1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: ![]() .
.
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 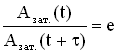 , а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 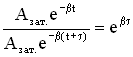 . Из этих соотношений следует βτ = 1, отсюда
. Из этих соотношений следует βτ = 1, отсюда
![]() .
.
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
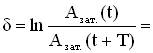
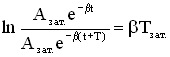
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
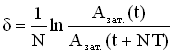 ,
,
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
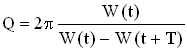 . Так как энергия пропорциональна квадрату амплитуды, то
. Так как энергия пропорциональна квадрату амплитуды, то 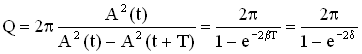 .
.
При малых значениях логарифмического декремента δ добротность колебательной системы равна
![]() ,
,
где Ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна 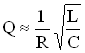 , а добротность пружинного маятника –
, а добротность пружинного маятника – 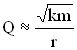 .Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
.Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω0 = β частота затухающих колебаний становится равной нулю ωзат. = 0, а Тзат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω0 = β запишется так: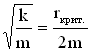 , откуда найдем величину критического коэффициента сопротивления:
, откуда найдем величину критического коэффициента сопротивления:
![]() .
.
Для LCR – контура условие 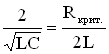 позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
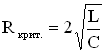 .
.
 3
3