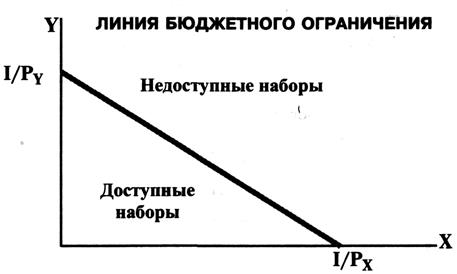
2.2. Бюджетные ограничения для потребителя
Потребительский выбор всегда осуществляется в рамках ресурсных, или бюджетных ограничений. Предположим, покупатель потребляет только два товара: ананасы (а) и бисквиты (b). Рыночная цена ананасов – Ра, а бисквитов – Рb. Пусть сумма денег,
которую может израсходовать потребитель – I. Бюджетное ограничение
потребителя требует, чтобы сумма денег, затраченная на оба товара, не
превышала общей суммы денег, которую может израсходовать потребитель. Тогда
потребителю доступны все товарные наборы, которые стоят не дороже I. Это
доступное потребителю множество товаров – бюджетное
множество можно записать в виде:
PaQa
+ PbQb ≤ I,
где Qa –
количество товара а, а Qb –
количество товара b в потребительском
наборе, PaQa – сумма денег, расходуемая потребителем на
товар а, PbQb
-– сумма денег, расходуемая на товар b.
Предположим, для
простоты, что потребитель тратит на покупку товаров сумму I полностью. Тогда все наборы из
бюджетного множества, стоимость которых точно равна I, будут лежать на бюджетной линии, которая должна удовлетворять требованию
PaQa + PbQb = I (1)
Пример.
Предположим, что ваш недельный бюджет, который вы можете использовать на
покупку двух товаров ананасов и бисквитов составляет 120 руб. и вы эту сумму
расходуете полностью. Пусть цена ананаса, Pa =10 руб., а цена
бисквита, Pb = 8 руб. Тогда вашим бюджетным ограничением будет:
10Qa +
8Qb = 120
Изобразим графически бюджетное множество и
бюджетную линию (рис. 2-7).
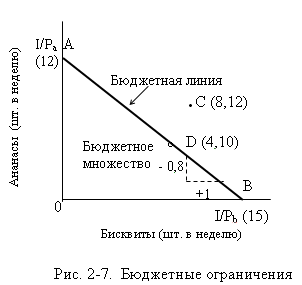 Вам, как потребителю, доступны все наборы, лежащие внутри бюджетного
Вам, как потребителю, доступны все наборы, лежащие внутри бюджетного
множества и на его границе АВ. Если бюджет
расходуется полностью, то выбранный вами набор представляет одна из
точек бюджетной линии АВ (За пределами бюджетной линии находятся недоступные
комбинации благ. Так, набор в точке С недоступен, поскольку для его
приобретения требуется 176 руб. (= 10·8
+ 8·12). Поэтому
бюджетная линия называется также границей
потребительских возможностей.
Составим уравнение бюджетной линии.
Это линейное уравнение типа: y = c + dx (2)
где y –количество первого
товара (ананасов), то есть Qa,
x – количество второго товара
(бисквитов) то есть Qb,
c – это вертикальное пересечение бюджетной линией оси ординат в
точке А (если x=0, то y = c),
d – это наклон линии, который
равен отношению вертикального изменения y
к горизонтальному изменению х.
Определим значение c
применительно к нашей задаче. Это количество ананасов (Qa), которое
в состоянии купить потребитель на всю сумму (I) , если он не будет покупать бисквиты вообще: с = I/Pa.
В нашем примере с = 120/10 = 12
(точка А).
Найдём, чему
равен наклон бюджетной линии d.
Наклон = – ∆Qa/∆Qb,
или: – ОА/ОВ.
ОА –это вертикальное пересечение, равное I/Pa.
ОВ –
это горизонтальное пересечение бюджетной линией оси абсцисс. ОВ показывает,
сколько бисквитов может купить потребитель на всю сумму (I), если он не
покупает ананасов вообще. ОВ = I/Рb. В нашем примере в точке В
потребитель покупает 15 бисквитов (=120/8). Таким образом,
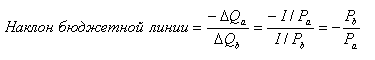 (3)
(3)
Наклон бюджетной
линии в нашем примере составит: – 0,8 (= – 12/ 15 или – 8/10).
Подставим найденные значения с и d в
уравнение (2). Уравнение бюджетной линии
выглядит:
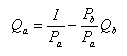 (4)
(4)
![]() Вопрос к аудитории (пример): Какое количество ананасов может позволить себе потребитель, если он решил купить 10 бисквитов?
Вопрос к аудитории (пример): Какое количество ананасов может позволить себе потребитель, если он решил купить 10 бисквитов?
![]() Ответ (нажмите, чтобы увидеть):
Ответ (нажмите, чтобы увидеть):
4 ананаса = (120/10 − 8 × 10/10)
Уравнение бюджетной линии (4) легко можно получить путём чисто формального преобразования уравнения бюджетного ограничения (1). Но для нас было важно вывести и определить смысл наклона бюджетной линии.
Наклон бюджетной линии (3) показывает от какого количества одного блага
(ананасов) должен при существующих
ценах отказаться потребитель, чтобы включить в свой набор дополнительную
единицу другого блага (бисквиты). В нашем примере он равен – 0,8. Это означает,
что потребитель должен пожертвовать 0,8 ананаса, чтобы купить ещё один бисквит.
Для приобретения бисквита нужно 8 рублей (цена 1 бисквита). Их потребитель
получит, если откажется от покупки 0,8 ананасов (именно такое количество
ананасов можно было купить на 8 руб. при цене 1 ананаса в 10 руб.). Но то
количество блага, которым приходится жертвовать ради получения данного блага
есть не что иное как альтернативная стоимость (opportunity cost), или издержки
приобретения данного блага. (Напомним, что альтернативная стоимость – это не особый вид издержек, а правильный
взгляд на любые издержки. Деньги, которые мы тратим, чтобы что-нибудь купить,
являются издержками только потому, что существуют другие вещи, которые мы могли
бы купить на эти деньги). Отсюда следует важный вывод, который будет нам
полезен потом, при нахождении потребительского оптимума: наклон бюджетной линии отражает предельные издержки приобретения
дополнительной единицы блага.
Из уравнения (3) также видно, что наклон
бюджетной линии показывает соотношение цен товаров, входящих в потребительский
набор, точнее, отношение цены замещающего товара (бисквит), к цене
замещаемого товара (ананас).
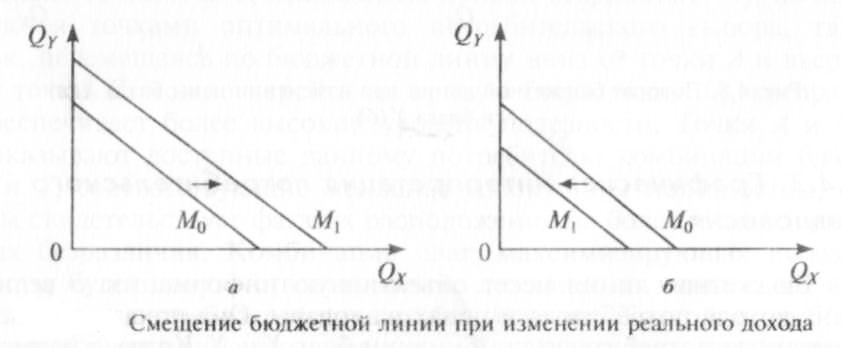
При изменении цен товаров и дохода изменяется множество товаров,
доступное потребителю и, следовательно, положение бюджетной линии.
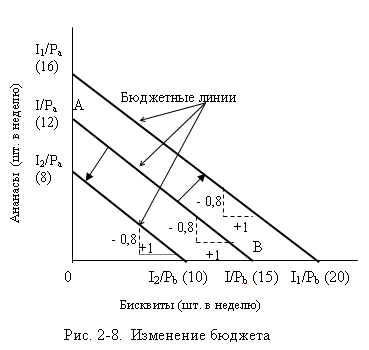
Изменение дохода при тех же товарных ценах
ведёт к параллельному сдвигу бюджетной линии. Её наклон не меняется – ведь
соотношение цен остаётся прежним. На рис.2-8 отражены два случая – изменение
бюджета (мы продолжаем наш пример) с I = 120 руб. до I1 = 160
руб., и с с I = 120 руб. до I2 = 160
руб. В случае увеличения суммы, предназначенной для расходов, бюджетная линия
сдвигается вверх, в случае уменьшения – вниз.
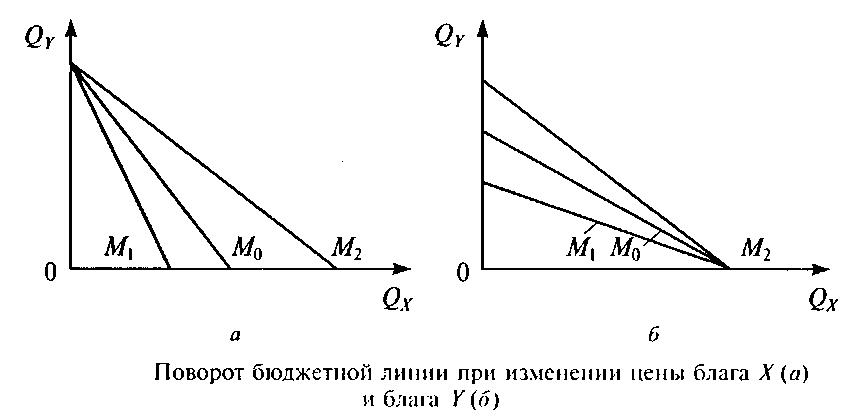
В случае изменения цен при неизменном доходе положение бюджетной линии
также меняется. Рассмотрим два случая.
Первый. Если изменяется цена одного товара, а
бюджет и цена второго товара те
же, то бюджетная линия меняя наклон (соотношение цен изменилось!)
поворачивается вокруг точки пересечения бюджетной линии с координатной осью, на
которой показывается количество товара, цена которого не претерпела изменения.
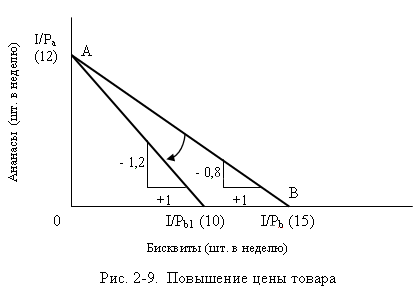
Пусть цена бисквитов повышается с Pb = 8 до Pb1 = 12 руб.
(см. рис. 2-9).
Тогда, максимальное количество бисквитов, которое может купить
потребитель на свой доход I = 120 руб. уменьшается с 15 штук до 10. Максимально
возможное количество другого товара в наборе (ананасов) по-прежнему равно 12,
ведь ни его цена, ни доход не изменились. Наклон бюджетной линии увеличился (по
модулю) с Pb/Pa = – 0,8 до Pb1/Pa =
– 1,2 (= -12/10).
Если бюджетная линия стала круче, значит
цена товара, показываемого по горизонтальной оси, снизилась. Если же
произойдёт понижение цены, то бюджетная линия повернётся вокруг точки А направо
и её наклон уменьшится. Если бюджетная
линия стала более пологой то это означает, что относительная цена товара по
горизонтальной оси понизилась.
Если обе цены изменяются в одинаковой пропорции, а бюджет остаётся тем
же, то наклон бюджетной линии не меняется, но происходит её параллельный сдвиг
– верх, если цены понизились и вниз,
если цены повысились. Если наряду с ценами в такой же пропорции изменяется
бюджет потребителя, то бюджетная линия останется в прежнем положении. Значение
для наклона и положения бюджетной линии имеет относительное, а не абсолютное
изменение цен.
На бюджетное
ограничение потребителя кроме цен и бюджета (дохода) оказывают также влияние
налоги, субсидии, рационирование благ правительством. Бюджетная линия может
прерываться, становится ломаной. Её конкретная форма зависит от обстоятельств.
Мы вернёмся к этому вопросу на лекции после рассмотрения потребительского
оптимума, а также на семинарах при решении различных задач.
Увеличением дохода потребителя или пропорциональным снижением цен на товары Х и Y.
Задача 6в. Чем вызван сдвиг бюджетной линии?

Снижением цены товара Y.
Задача 7а. Дана бюджетная линия потребителя.
Цена товара Y – 10. Каков доход потребителя?

Решение: Если Х = 0, то весь доход тратится на товар Y, количество которого равно 15. Отсюда доход равен 15 • 10 = 150.
Задача 7б. Дана бюджетная линия потребителя.
Цена товара Х – 100. Каков доход потребителя? 1000

Задача 7в. Дана бюджетная линия потребителя.
Цена товара Y – 50. Каков доход потребителя? 1500

Задача 8а. Дана бюджетная линия потребителя с доходом 120 ед.
Найти уравнение бюджетной линии.

Решение:Если Х = 0, то весь доход тратится на товар Y, количество которого равно 10. Отсюда цена товара Y = 120 / 10 = 12. Если Y = 0, то весь доход тратится на товар Х, количество которого равно 20. Отсюда цена товара Х = 120 / 20 = 6.
Уравнение бюджетной линии 12Y + 6Х = 120.
Задача 8б.Дана бюджетная линия потребителя с доходом 200 ед.
Найти уравнение бюджетной линии. 20Y + 20Х = 200.

Задача 8в.Дана бюджетная линия потребителя с доходом 500 ед.
Найти уравнение бюджетной линии.5Y + 10Х = 500.

Задача 9а.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Y равна 5 рублей. Найти уравнение бюджетной линии.

Решение:Как в задаче 7а находим доход потребителя – 30 • 5 = 150. Как в задаче 8а находим уравнение бюджетной линии: 5Y + 10Х = 150, или иначе Y = (150 – 10Х) / 5 = 30 – 2Х.
Задача 9б.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Х равна 10 рублей. Найти уравнение бюджетной линии. 30Y + 10Х = 300, или Y = 10 – 1/3Х.

Задача 9в.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Y равна 2 рубля. Найти уравнение бюджетной линии.2Y + 3Х = 120, или Y = 60 – 1,5Х.

Тема: Теория производства
Задача 1а. Затраты фирмы на производство 10 тыс. единиц продукции в течение года составили: заработная плата – 25 млн. руб.; сырье и материалы – 9 млн. руб. Кроме того, фирма арендовала производственные помещения за 48 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 300 млн. руб., а срок окупаемости – 10 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 100% выпущенных изделий по цене 12 тыс. руб. за штуку. Определите прибыль, накопленную к концу года.
Решение: Затраты фирмы составляют: 25 млн. руб. (заработная плата) + 9 млн. руб. (сырье и материалы) + 48 млн. руб. (аренда) + 30 млн. руб. (300/10 – амортизация оборудования) = 112 млн. руб.
Доход составил 10 тыс. единиц • 12 тыс. руб. за штуку = 120 млн. руб.
Прибыль равна 120 – 112 = 8 млн. руб.
Задача 1б. Затраты фирмы на производство 15 тыс. единиц продукции в течение года составили: заработная плата – 50 млн. руб.; сырье и материалы – 18 млн. руб. Кроме того, фирма арендовала производственные помещения за 96 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 600 млн. руб., а срок окупаемости – 10 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 100% выпущенных изделий по цене 16 тыс. руб. за штуку. Определите прибыль, накопленную к концу года.
Млн. руб.
Задача 1в.Затраты фирмы на производство 12 тыс. единиц продукции в течение года составили: заработная плата – 5 млн. руб.; сырье и материалы – 2 млн. руб. Кроме того, фирма арендовала производственные помещения за 9 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 60 млн. руб., а срок окупаемости – 6 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 80% выпущенных изделий по цене 3 тыс. руб. за штуку. Определите прибыль, накопленную к концу года. 2,8 млн. руб.
Задача 2а. Открыв новое дело, бизнесмен вложил в него собственный капитал 80 000. Он мог взять эту сумму в банке под 10 % годовых. Когда после полутора лет работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки?
Решение: Неявные издержки равны процентам, которые бизнесмен заплатил бы, если бы взял деньги в банке. 1,5 года • (80 000 • 0,1) = 12 000.
Задача 2б. Открыв новое дело, бизнесмен вложил в него собственный капитал 20 000. Он мог взять эту сумму в банке под 5 % годовых. Когда после двух лет работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки? 2000
Задача 2в. Открыв новое дело, бизнесмен вложил в него собственный капитал 100 000. Он мог взять эту сумму в банке под 20 % годовых. Когда после полугода работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки? 10000
Задача 3а. Фирма увеличивает применяемый капитал со 12 до 15 ед., используемый труд с 50 до 62,5 ед. Выпуск продукции при этом увеличился с 20 до 22 ед. Какой эффект роста масштаба производства имеет место в данной ситуации?
Решение: Фирма увеличила ресурсы в 1,25 раз (15/12 и 62,5/50), а выпуск увеличился в 1,1 раз (22/20). Это убывающий эффект масштаба производства.
Задача 3б. Фирма увеличивает применяемый капитал с 240 до 300 ед., используемый труд с 1000 до 1250 ед. Выпуск продукции при этом увеличился с 400 до 440 ед. Какой эффект роста масштаба производства имеет место в данной ситуации? Убывающий эффект масштаба производства
Задача 3в. Фирма увеличивает применяемый капитал со 160 до 320 ед., используемый труд с 50 до 100 ед. Выпуск продукции при этом увеличился с 300 до 700 ед. Какой эффект роста масштаба производства имеет место в данной ситуации? Возрастающий эффект масштаба производства
Задача 4а. Функция предельных затрат фирмы МС = 10 + Q (руб.). Цена единицы продукции постоянна и равна 60 руб./шт. Определите объем выпуска, который позволит фирме максимизировать прибыль.
Решение: Фирма максимизирует прибыль при МС = МR, который в условиях совершенной конкуренции равен цене единицы продукции, т.е. 60 руб. Поэтому МR = 60. Откуда МС = 60, а Q = 50.
Задача 4б. Функция предельных затрат фирмы МС = 60 + 2Q (руб.). Цена единицы продукции постоянна и равна 100 руб./шт. Определите объем выпуска, который позволит фирме максимизировать прибыль. 20
Задача 5а. Заполнить таблицу.
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
Решение:
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
| ТР = АР•L= 20•3 = 60 | – (найти по этим данным нельзя) | ||
| АР = ТР/L=80/4=20 | ΔТР / Δ L = 20 / 1 = 20 | ||
| ТР5 = ТР4 + МР = 80+10=90 | АР = ТР/L = 90/5 = 18 | ||
| АР = ТР/L = 96/6 = 16 | ΔТР / Δ L = 6 / 1 = 6 |
Задача 5б. Заполнить таблицу.
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
| – |
Задача 5в. Заполнить таблицу.
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
| Кол-во труда | Общий продукт, ТР | Средний продукт, АР | Предельный продукт, МР |
| – |
Задача 6а. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.
| Количество используемого труда, L |
| Совокупный продукт, ТР |
| Средний продукт, АР |
| Предельный продукт, МР |
Решение:
| Количество используемого труда, L | ||||||
| Совокупный продукт, ТР | ||||||
| Средний продукт, АР = ТР / L | 35/1=35 | 80/2=40 | 123/3=41 | 156/4=39 | 177/5=35,4 | 180/6=30 |
| Предельный продукт, МР = ΔТР / Δ L | 35-0=35 | 80-35=45 | 123-80=43 | 156-123=33 | 177-156=21 | 180-177=3 |
Задача 6б. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.
| Количество используемого труда, L |
| Совокупный продукт, ТР |
| Средний продукт, АР |
| Предельный продукт, МР |
| Количество используемого труда, L |
| Совокупный продукт, ТР |
| Средний продукт, АР |
| Предельный продукт, МР |
Задача 6в. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.
| Количество используемого труда, L |
| Совокупный продукт, ТР |
| Средний продукт, АР |
| Предельный продукт, МР |
| Количество используемого труда, L |
| Совокупный продукт, ТР |
| Средний продукт, АР |
| Предельный продукт, МР |
Задача 7а.Производственная функция Q = 5L 0,5 • К 0,5 , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 9 ч труда и 9 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех удвоил затраты обоих ресурсов.
Решение: Если в день затрачивается 9 ч труда и 9 ч работы машин, то L = К = 9. Тогда выпуск продукции составит Q = 5L 0,5 х К 0,5 =5 х 9 0,5 х 9 0,5 =45единиц.
Если цех удвоил затраты обоих ресурсов, то L = К = 9 • 2 = 18, а выпуск составит Q = 5 • 18 0,5 • 18 0,5 =90 единиц.
Задача 7б.Производственная функция Q = 4L 0,5 • К , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 4 ч труда и 4 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех удвоил затраты обоих ресурсов. 32; 90,5
Задача 7в.Производственная функция Q = 25L 0,25 • К 0,25 , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 16 ч труда и 16 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех в 4 раза увеличил затраты обоих ресурсов. 100, 200
Задача 8а.Фирма работает по технологии с производственной функцией Q = L 0,5 • К 0,25 . Во сколько раз увеличится выпуск продукции фирмой, если она в 2 раза увеличит использование обоих ресурсов?
Решение:Еслифирма в 2 раза увеличит использование обоих ресурсов, то выпуск составит Q = (2L) 0,5 х (2К) 0,25 = 2 0,5 х L 0,5 х 2 0,25 х К 0,25 = 2 0,5 х 2 0,25 х (L 0,5 х К 0,25 ), т.е. увеличится в 2 0,5 х 2 0,25 или в 2 0,75 ≈ 1,68 раз.
Задача 8б.Фирма работает по технологии с производственной функцией Q = 4 L 0,5 х К 0,5 . Во сколько раз увеличится выпуск продукции фирмой, если она в 4 раза увеличит использование обоих ресурсов? 4
Задача 8в.Фирма работает по технологии с производственной функцией Q = 5 L 0,25 • К 0,5 . Во сколько раз увеличится выпуск продукции фирмой, если она в 16 раз увеличит использование обоих ресурсов? 8
Задача 9а.Производственная функция: Q = L 0,5 • К 0,5 . В день затрачивается 4 ч труда и 4 ч работы машин.
Определить: а) количество выпускаемой продукции; б) средний продукт труда.
Решение: Количество выпускаемой продукции Q = L 0,5 • К 0,5 = 4 0,5 • 4 0,5 = 4 единицы.
Средний продукт труда равен Q / L = 4 /4 = 1.
Задача 9б.Производственная функция: Q = 4 L 0,25 • К 0,25 . В день затрачивается 16 ч труда и 9 ч работы машин.
Определить: а) количество выпускаемой продукции; б) средний продукт капитала. 13,86; 1,54.
Задача 9в.Производственная функция: Q = 2 L 0,25 • К 0,5 . В день затрачивается 256 ч труда и 225 ч работы машин. 120, 0,47.
Определить: а) количество выпускаемой продукции; б) средний продукт труда.
Задача 10а.Процесс производства на предприятии описывается функцией Q = 80 + 10К 2 + 10L, где К – количество капитала, а L – количество труда. Найти предельный продукт труда.
Решение: Необходимо найти производную для L, принимая, что К = const. Тогда (10L)’ = 10.
Задача 10б.Производственная функция определяется уравнением Q = 100 + 12К 2 + 15L, где К – количество капитала, а L – количество труда. Найти предельный продукт капитала. 24К
Задача 10в.Производственная функция определяется уравнением Q = 20 + 6К + 20L 2 , где К – количество капитала, а L – количество труда. Найти предельный продукт труда. 40L
Задача 11а. Два работника вместе производят 80 ед. продукции, а три работника – 100 ед. продукции. Найти предельный продукт третьего работника.
Решение: 100 – 80 = 20 ед.
Задача 11б. Четыре работника вместе производят 120 ед. продукции, а пять работников – 128 ед. продукции. Найти предельный продукт пятого работника. 8
Задача 12а. Совокупный доход фирмы, производящей радиоприемники, составляет 1000 ден. единиц в месяц при объеме выпуска 500 штук в месяц, постоянные издержки равны 800 ден. единиц в месяц, а переменные – 100 ден. единиц в месяц. Чему равна средняя прибыль фирмы?
Решение: Средняя прибыль равна отношению общей прибыли к объему выпуска продукции: АРr = Рr / Q = (1000 – (800+100)) / 500 = 0,2 ден. единиц.
Задача 12б. Совокупный доход фирмы составляет 2000 ден. единиц в месяц при объеме выпуска 800 штук в месяц, постоянные издержки равны 400 ден. единиц в месяц, а переменные – 1200 ден. единиц в месяц. Чему равна средняя прибыль фирмы? 0,5
Тема: Издержки производства
Задача 1а. Заполните таблицу и определите оптимальный объем производства.
| Q | TC | FC | VC | AC | AFC | AVC | MC |
Решение: Т.к. при Q = 0,VC = 0, поэтому FC = 50.
VC = TC – FC. АС = ТС / Q. АFС = FС / Q. AVC = VС / Q. МС = ∆ TC
| Q | TC | FC | VC | AC | AFC | AVC | MC |
| – | – | – | – | ||||
| 12,5 | 37,5 |
Задача 1б. Заполните таблицу и определите оптимальный объем производства.
| Q | TC | FC | VC | AC | AFC | AVC | MC |
| Q | TC | FC | VC | AC | AFC | AVC | MC |
| – | – | – | – | ||||
| 37,5 | 107,5 |
Задача 1в. Заполните таблицу и определите оптимальный объем производства.
| Q | TC | FC | VC | AC | AFC | AVC | MC |
| Q | TC | FC | VC | AC | AFC | AVC | MC |
| – | – | – | – | ||||
| 3,33 | |||||||
| 2,5 | 7,5 |
Задача 2а. Функция общих затрат фирмы имеет вид ТС = 10Q – Q 2 + 0,05Q 3 . Определить величину предельных затрат фирмы при Q = 4.
Решение: Находим производную функции общих издержек. Получаем (ТС)’ = 10 – 2Q + 0, 15Q 2 . При Q = 4 значение равно 4,4.
Задача 2б. Функция общих затрат фирмы имеет вид ТС = 20Q – 2Q 2 + 0,1Q 3 . Определить величину предельных затрат фирмы при Q = 3. 10,7
Задача 2в.Функция общих затрат фирмы имеет вид ТС = 60Q – 4Q 2 + 0,2Q 3 . Определить величину предельных затрат фирмы при Q = 6. 33,6
Задача 3а. Функция средних переменных затрат имеет вид: AVС = 100 + 20Q. Постоянные затраты равны 120. Найти алгебраическое выражение для функций общих затрат.
Решение: ТС = FC + VС, а VС = AVС • Q, поэтому ТС = 120 + 100Q + 20Q 2 .
Задача 3б.Функция средних переменных затрат имеет вид: AVС = 200 + 50Q. Постоянные затраты равны 400. Найти алгебраическое выражение для функций общих затрат. 400 + 200Q + 50Q 2 .
Задача 3в.Функция средних переменных затрат имеет вид: AVС = 400 + 60 Q. Постоянные затраты равны 500. Найти алгебраическое выражение для функций общих затрат. 500 + 400Q + 60Q 2 .
Задача 4а. При производстве 40 шт. деталей АVС = 20 руб. При выпуске 20 шт. АFС = 10 руб. При выпуске 50 шт. АС = 60 руб. Определите АС при производстве 40 шт. и АVС при 50 шт. деталей.
Решение:Дано
Составим таблицу, дополним и заполним ее.
| Q | ТС | АС = АFС+АVС | FС | АFС = FС / Q | VС | АVС |
| 200 = 20•10 | 10 (по условию) | |||||
| 1000 = 40 • 25 | 25 = 5 + 20 | 5 = 200/40 | 800 = 1000 – 200 | (по условию) | ||
| 60 (по условию) | 4 = 200/50 | 56 = 60 – 4 |
АС при производстве 40 шт. равна 25, АVС при 50 шт. деталей равна 56.
Задача 4б. При производстве 20 шт. деталей АVС = 10 руб. При выпуске 10 шт. АFС = 5 руб. При выпуске 25 шт. АС = 30 руб. Определите АС при производстве 20 шт. и АVС при 25 шт. деталей. 12,5; 28
Задача 5а. Функция издержек конкурентной фирмы ТС = Q 2 + 5Q + 25. Определите функции переменных, постоянных, средних переменных, средних постоянных, средних общих и предельных затрат.
Решение:
переменные издержки – VС = ТС-FС = Q 2 + 5Q;
постоянные издержки – FС = const = 25;
средние переменные издержки – АVС = VС/ Q = (Q 2 + 5Q / Q = Q + 5;
средние постоянные издержки – FС / Q = 25 / Q
средние общие издержки – АС = ТС/ Q = (Q 2 + 5Q + 25) / Q = Q + 5 + 25 / Q;
предельные издержки – МС = (Q 2 + 5Q + 25)’ = 2Q + 5.
Задача 6а. Средние издержки фирмы составляют 10 и с ростом объема выпуска не изменяются. Насколько увеличатся издержки фирмы при увеличении выпуска с 1000 до 1500 ед. продукции.
Решение: Т.к. средние издержки неизменны, ∆ТС = АС • ∆Q = 10 • (1500 – 1000) = 5000.
Задача 6б. Средние издержки фирмы составляют 20 и с ростом объема выпуска не изменяются. Насколько увеличатся издержки фирмы при увеличении выпуска с 60 до 80 ед. продукции. 400
Задача 7а.Даны объем производства, валовые постоянные и средние переменные издержки. Найти средние валовые издержки при производстве двух единиц продукции.
| Объем производства, ед. |
| Валовые постоянные издержки, руб. |
| Средние переменные издержки, руб. |
Решение: Средние валовые издержки АС = АFС + АVС. АFС = FС / Q = 30 / 2 = 15. АVС по условию 55. Итого ответ 70. Задачу можно решить другим способом. АС = ТС / Q. ТС = VС + FС. VС = АVС • Q = 55 • 2 = 110. FС по условию 30. Ответ: (110 + 30) / 2 = 70.
Задача 7б.Даны объем производства, средние постоянные и средние переменные издержки. Найти валовые издержки при производстве трех единиц продукции. 240
| Объем производства, ед. |
| Средние постоянные издержки, руб. |
| Средние переменные издержки, руб. |
Задача 8а. Q = 100, FC = 250; AVC = 35. Найти общие издержки.
Решение:ТС = FC + VC = FC + АVC • Q = 250 + 35 • 100 = 3750
Задача 8б. Q = 20, АFC = 5; AVC = 25. Найти общие издержки. 600
Последнее изменение этой страницы: 2016-07-22; просмотров: 1779
Теория поведение потребителей (стр. 3 )
 |
Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |

Для данного случая: 
Предельные полезности должны относиться как 2:1. Таких сочетаний несколько:
I сочетание: 1 литр молока (MUм=10) и 3 буханки хлеба (MUх=5), т. е. 1-я и 3-я позиции.
II сочетание: 2 литра молока (MUм=8) и 4 буханки хлеба.
Проверим эти сочетания на бюджетное ограничение (2,5 д. ед.).
I сочетание: 1 литр молока ´ 1д. ед. + 3 буханки хлеба ´ 0,5 = 2,5 д. ед.
II сочетание: 2 литра молока ´ 1д. ед + 4 буханки хлеба ´ 0,5 = 4 д. ед.
Бюджетное ограничение позволяет уравновесить только первое сочетание
Вывод: Q М опт. =1 литр; Q м опт. = Q Хопт. = 3 буханки.
Задача №6 на количественный подход к анализу полезности и определение оптимума потребителя: Марина получает от родителей 6 д. е. в неделю на карманные расходы. Эти деньги она тратит на покупку жвачки и конфет. Каждая жвачка стоит 2 д. е., а каждая конфета – 1 д. е. Полезность для Марины каждую неделю складывается из полезности жвачки и полезности конфет. Две составляющие функции полезности представлены табличным способом:
Взвешенная предельная полезность
Взвешенная предельная полезность
1) Заполните пропуски в таблице. 2) Какой потребительский набор выберет Марина?
1) Заполним таблицу
Ответы получены из простых формул:
Предельная полезность: MU = ∆TU / ∆Q = TUn – TUn – 1 / Qn – Qn – 1;
Взвешенная предельная полезность: MUЖ1/РА; MUК1/РВ и т. д.
2) Марина получит максимум полезности, если распределит свой бюджет:
I = PХ*QХ+ PY*QY так, что МUж/Pж = MUк/Pк, при этом бюджет Марины ограничен 6 д. е.
С учетом бюджетных ограничений оптимальная структура покупки для Марины – это 2 жвачки и 2 конфеты, при этом весь бюджет потребителя истрачен, а структура покупки максимально удовлетворит потребности Марины.
Задача №7 на построение кривых безразличия: Постройте кривые безразличия полезности: 1) для двух взаимодополняющих товаров в пропорции 3 : 1; 2) для двух абсолютно взаимозаменяемых товаров пропорции 3 : 1.

Задача №8 на определение предельной нормы замещения: Найти предельную норму замещения товара У товаром Х при переходе от набора В к набору С.
Предельная норма замещения представляет собой то количество одного товара Y, которое потребитель готов заменить единицей другого товара X:
MRS x/y = –  Qy/
Qy/  Qx.
Qx.
 Предельная норма замещения товара У товаром Х при переходе от набора В к набору С равна:
Предельная норма замещения товара У товаром Х при переходе от набора В к набору С равна:
MRS x/y = –  Qy/
Qy/  Qx = – (8-10) / (12-8) = 2 / 4 = 0,5.
Qx = – (8-10) / (12-8) = 2 / 4 = 0,5.
Задача №9 на порядковый подход к определению количества благ в оптимальном наборе потребителя: Предельная полезность X для индивида отображается функцией MUХ = 40 – 5*Х, а предельная полезность Y: MUY = 20 – 3*Y. Известны цены благ и доход индивида: PХ = 5; PY=1; I=20. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?
Потребитель получит максимум полезности, если распределит свой бюджет:
I = PХ*QХ+ PY*QY так, что MUХ/PХ = MUY/PY.
Получаем систему из двух уравнений:

Задача №10 на порядковый подход к анализу полезности и определение цены благ в оптимальном наборе потребителя: Функция полезности для данного потребителя U = 4xy, а доход, выделенный им для покупки данных товаров, равен 24 д. е. В оптимальный набор вошли 2 единицы первого блага (Х) и 3 – второго блага (Y). Чему в этом случае равны цены первого и второго благ?
Оптимальный набор должен соответствовать условию бюджетного ограничения:
I = PХ*QХ+ PY*QY  2*Рх + 3*Ру = 24.
2*Рх + 3*Ру = 24.
Одновременно соотношение цен двух товаров в оптимальм наборе равно соотношению их предельных полезностей: MUx / MUy = Px / Py.
Предельная полезность определяется как первая производная функции полезности:
МUx = dTU / dQХ = 4y; МUy = dTU / dQy = 4x.
Отсюда, МUx = 4*3= 12, МUy = 4*2 = 8.
Поэтому Рх / Ру = 12 / 8 = 3/2.
Можно выразить Рх = 3/2 Ру.
Затем, подставив это выражение в уравнение бюджетного ограничения, получим:
2 * 3/2 Ру + 3Ру = 24
Тогда Рх = 3/2 * Ру = 3/2 * 4=6.
Задача №11 на определение уравнения бюджетной линии: Недельный доход Петрова 40 ден. ед. Он расходует его на хлеб и молоко. Вопрос: а) Если цена буханки хлеба 4, а цена литра молока 10, то каково уравнение бюджетной линии; б) как изменится уравнение бюджетной линии, если доход Петрова уменьшится до 20; в) сколько буханок хлеба смог бы купить Петров, если бы отказался от молока.
А) Подставим данные из условия задачи в уравнение бюджетной линии: .
.
4 • Qх + 10 • Qм = 40.
Б) Если доход Петрова уменьшится до 20, то уравнение будет выглядеть:
4 • Qх + 10 • Qм = 20.
В) Если бы Петров отказался от молока, то уравнение будет выглядеть:
4 • Qх + 10 • 0 = 40.
Откуда Qх = 10 буханок.
Задача №12 на анализ бюджетной линии и определение дохода потребителя: На рисунке дана бюджетная линия потребителя. Цена товара Y – 10. Каков доход потребителя?

Подставим данные из условия задачи в уравнение бюджетной линии:  .
.
Если Х = 0, то весь доход тратится на товар У, количество которого равно 15.
Отсюда доход равен 15 • 10 = 150.
Задача №13 на анализ бюджетной линии и определение функции бюджетного ограничения: На рисунке дана бюджетная линия потребителя с доходом 120 ед. Найти уравнение бюджетной линии.

Если Х = 0, то весь доход тратится на товар У, количество которого равно 10.
Отсюда цена товара У = 120 / 10 = 12.
Если У = 0, то весь доход тратится на товар Х, количество которого равно 20.
Отсюда цена товара Х = 120 / 20 = 6.
Подставим полученные данные в уравнение бюджетной линии:  .
.
Уравнение бюджетной линии 12 У + 6 Х = 120.
Задача №14 на анализ сдвига бюджетной линии: 1) Чем вызван сдвиг бюджетной линии на рисунке?

2) Допустим, потребитель имеет доход 1000 д. е. в месяц и весь он должен быть израсходован на покупку двух товаров А и Б. Товар А стоит 25 д. е., а товар Б — 50 д. е. Нарисуйте бюджетную линию (2).
3) Какой будет бюджетная линия (3), если доход потребителя вырастает до 1200 д. е.?
4) Какой будет бюджетная линия (4)при доходе 1000, но снижении цены товара А до 20 д. е.
1) Из условия бюджетного ограничения I = PА*QА+ PБ*QБ следует, что сдвиг бюджетной линии (1) на рисунке вызван увеличением цены товара, ведь в этом случае его можно будет купить меньше.
2) Уравнение бюджетной линии (2): 1000 = 25*QА+ 50*QБ.
Бюджетную линию (2) строим по двум точкам:
Если QБ=0, то QА=40;
Если QА=0, то QБ=20.
3) Уравнение бюджетной линии (3): 1200 = 25*QА+ 50*QБ.
Бюджетную линию (3) строим по двум точкам:
Если QБ=0, то QА=48;
Если QА=0, то QБ=24.
4) Уравнение бюджетной линии (4): 1000 = 20*QА+ 50*QБ.
Бюджетную линию строим по двум точкам:
Если QБ=0, то QА=50;
Если QА=0, то QБ=20.






 А А А
А А А

 40 48 50
40 48 50
Задача №15 на порядковый подход к анализу полезности и оптимума потребителя: Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден. ед. Цены благ соответственно равны РX = 20, РY= 40. Чему будет равен набор для потребителя? Представьте решение и аналитически, и графически.
Запишем задачу в общем виде: 
Поскольку оптимум в этом примере является внутренним, то должно выполняться условие 
Таким образом, оптимальный набор должен находиться на прямой х = 2у и в то же время удовлетворять бюджетному ограничению.
Получаем систему из 2-х линейных уравнений:

Ее решение дает оптимальный набор: 
Графическая интерпретация этой задачи:

Задача №16 на анализ и построение линии «цена–потребление»: Бюджет индивида равен 200 ден. ед. При цене блага  его линия «цена–потребление» отображается формулой
его линия «цена–потребление» отображается формулой  1) На сколько единиц индивид изменит потребление каждого блага при снижении цены блага X с 5 до 4 ден. ед.? 2) Используя данные задачи, постройте кривую спроса.
1) На сколько единиц индивид изменит потребление каждого блага при снижении цены блага X с 5 до 4 ден. ед.? 2) Используя данные задачи, постройте кривую спроса.
1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «цена–потребление» (точкой касания бюджетной линии с кривой безразличия).
Системы уравнений при PX = 5 и PX = 4 соответственно:


Тогда ΔX = 20-18 = 2 ед., ΔY = 24-22 = 2 ед.
2) Пункт 2 выполните самостоятельно.
Задача №17 на анализ линии «доход–потребление» и построение кривой Энгеля: При ценах РX = 4; Рy = 5 линия «доход–потребление» индивида имеет вид:  1) На сколько единиц индивид увеличит потребление каждого блага при увеличении его бюджета с 333 до 375 ден. ед? 2) Постройте кривую Энгеля.
1) На сколько единиц индивид увеличит потребление каждого блага при увеличении его бюджета с 333 до 375 ден. ед? 2) Постройте кривую Энгеля.
1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «доход–потребление» (точкой касания бюджетной линии с кривой безразличия).
Системы уравнений при бюджетах 333 и 375 ден. ед. соответственно:


Тогда потребление блага X изменится на 25-22 = 3 ед., потребление блага Y изменится на 55-49 = 6 ед.

Рис. 1.2. Линия «доход–потребление»
2) Пункт 2 выполните самостоятельно.
3.7. Примеры ответов на тесты
Тест 3.1
Среди следующих утверждений одно является неправильным. Укажите на него:
а) Каждая точка на кривой безразличия означает разную комбинацию двух товаров;
б) Каждая точка на бюджетной линии означает различную комбинацию двух товаров;
в) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей;
г) Все точки на бюджетной линии означают одинаковый уровень денежного дохода;
д) Все точки на кривой безразличия означают одинаковый уровень денежного дохода.
Правильный ответ д).
Данное утверждение является неверным, так как по определению все точки на кривой безразличия означают различные комбинации двух товаров (а), соответствующие одинаковому уровню удовлетворения потребностей (в). Ответы б) и г) относятся к характеристике бюджетной линии и являются верными.
Тест 3.2
Увеличение дохода потребителя графически выражается в:
а) изменении наклона бюджетной линии;
б) параллельном сдвиге бюджетной линии вправо;
в) параллельном сдвиге бюджетной линии влево;
г) уменьшении наклона бюджетной линии;
д) увеличении наклона бюджетной линии.
Правильный ответ б).
Увеличение дохода потребителя означает расширение его возможностей. То есть потребитель получает возможность приобретать большие количества товаров при большем доходе и неизменном уровне цен или при неизменном доходе и снижении цен. Параллельный сдвиг бюджетной линии влево означает уменьшение дохода (в). Изменение наклона бюджетной линии (а): как уменьшение (г), так и увеличение (д) означает изменение в соотношении цен потребляемых благ.
Тест 3.3
Эффект дохода имеет место в следующем случае:
а) Если доходы людей падают, они покупают меньше данного товара;
б) Удешевление товаров приводит к тому, что потребитель может купить больше данного товара, не сокращая объем приобретения других товаров.
В) Объем покупок некоторых товаров сокращается по мере увеличения доходов людей.
Г) По мере того, как доходы людей растут, они сберегают увеличивающуюся часть дохода.
д) Во всех перечисленных случаях.
Правильный ответ б).
Эффект дохода состоит в увеличении возможности удовлетворения потребностей от приобретения товаров либо за счет увеличения дохода при неизменном уровне цен, либо за счет снижения цен при неизменном уровне дохода. Ответ а) и б) определяют сокращение возможностей удовлетворения потребностей. Ответ г) связан с проблемой распределения дохода и характеристикой динамики функции сбережения.
Тема 3.4
Цена товара Х составляет 1,5 руб. Цена товара У составляет 1 руб. Если потребитель оценивает предельную полезность товара У в 30 ютил. И желает максимизировать удовлетворение от покупки товаров Х и У, тогда он должен принять предельную полезность товара Х за:
д) В условии не содержится достаточной информации для ответа на вопрос.
Правильный ответ г).
Соотношение цен товаров равно соотношению их предельных полезностей: Mux / Muy = Px / Py. Поэтому Mux = Muy * Px / Py = 30*1,5 / 1 = 45 (ютил).
Тест 3.5
Предположим, что потребитель имеет доход в 8 долл. Цена товара А равна 1 долл., а цена товара В – 0,5 долл. Какая из следующих комбинаций товаров находится на бюджетной линии?
Правильный ответ г).
Следует исходить из условия бюджетного ограничения: Ра*А + Рв*В = Y. Таким образом, 1* 5 + 0,5* 6 = 8.
Тест 3.6
Общая полезность растет, когда предельная полезность:
в) увеличивается в медленном темпе;
г) увеличивается или уменьшается, но является величиной положительной;
д) является величиной отрицательной.
Правильный ответ г).
Предельная полезность – это прирост общей полезности в расчете на единицу прироста потребления продукта. Общая величина будет увеличиваться до тех пор, пока предельная (прирост) будет иметь положительное значение: если она уменьшается (а) и если она растет (б), даже если растет в медленном темпе (в). Но если предельная величина является отрицательной, общая величина начинает уменьшаться (д).
Тест 3.7
Потребительское равновесие на карте безразличия – это:
а) любое пересечение бюджетной линии и кривой безразличия;
б) любая точка на самой высокой из кривых безразличия;
в) та точка, в которой наклон бюджетной линии равен наклону касательной к ней кривой безразличия;
г) любая точка, расположенная на бюджетной линии;
д) любая точка, расположенная на пространстве, ограниченном бюджетной линией.
Правильный ответ в).
Равновесием потребителя в условиях бюджетных ограничений на графике является точка касания бюджетной линии самой высокой кривой безразличия. Это означает, что в данной точке наклон бюджетной линии и наклон кривой безразличия совпадают. Любое пересечение бюджетной линии и кривой безразличия (а) не может быть равновесием хотя бы потому, что неясно, какую именно кривую безразличия из всей совокупности на карте иметь в виду. Любая точка на самой высокой кривой безразличия (б) может не соответствовать величине бюджета потребителя, а любая точка на бюджетной линии (г) может не являться наилучшей с точки зрения оптимизации потребительских предпочтений.
3.8. Вопросы для самоконтроля
1. Охарактеризуйте общую и предельную полезность: их функции и взаимосвязь. Дайте графическую интерпретацию.
2. Ответьте на вопрос (парадокс А. Смита): “Почему вода, которая настолько необходима, что без нее невозможно жить, имеет такую низкую цену, в то время как у не столь необходимых алмазов такая высокая цена?”
3. Почему предельная полезность снижается?
4. Является ли рациональность естественным свойством человека? Привести примеры нерационального поведения потребителя?
5. Кардинализм и ординализм — два направления в теории потребительского выбора. Сформулировать их общие черты и различия.
6. Что мы понимаем под кривой безразличия? Какую информацию несет в себе кривая безразличия? Почему такие кривые являются: а) нисходящими; б) выпуклыми по отношению к началу координат?
7. Какие факторы определяют бюджетное ограничение потребителя? Какую информацию несет бюджетная линия? Как изменится положение бюджетной линии потребителя при уменьшении потребительского дохода? При удорожании блага X? Удешевлении блага У?
8. Проанализировать, как повлияет на решения потребителей о количестве приобретаемых благ введение Правительством более высоких ставок подоходного налога? Налога с продаж на продукты питания и предметы потребления?
9. Как можно определить (измерить) общую полезность, если известна предельная
10. полезность товара?
11. Каковы условия максимизации общей полезности?
12. В чем проявляется ограниченность теории предельной полезности?
13. Как проявляется эффект замещения в случае с гиффеновским товаром?
14. В чем заключается эффект Веблена?
15. «Эффект дохода» и «эффект замещения». Возможно ли их действие в противоположных направлениях?
1. Микроэкономика. Теория и российская практика: Учебник / Под ред.
вой, . М., КНОРУС, 2004. — Гл. 5.
2. Вэриан X. Микроэкономика. Промежуточный уровень. Современный подход. —
М.: Юнити, 1997. — Гл. 2—5.
3. , Игнатьев СМ., Микроэкономика. В 2-х т. — СПб.:
Экономическая школа, 2003. — Т. 1 — Гл. 5.
4. Курс экономической теории: Учебник / Под общей ред. ,
левой. — Киров: «АСА», 2002. — Гл.5, §9.
5. , Экономикс: Принципы, проблемы и политика: в 2-х
томах / Пер. с англ. 13-го изд. — М.: ИНФРА-М, 2001. — Т.2. —Гл.22— 23.
6. Нуреев P.M. Курс микроэкономики. — М.: Норма-Инфра-М, 2002. — Гл.4.
7. Общая экономическая теория (политэкономия): Учебник / Под общей ред. В. И.
Видяпина и . — М.: ПРОМО-Медия, 1995. — Гл. 17—18.
1. Алчиан Ар. А. Значение измерения полезности // Теория потребительского поведе
ния и спроса. — СПб.: Экономическая школа, 1993.
2. БлаугМ. Экономическая мысль в ретроспективе. — М., 1994. — С.306—343.
3. Дж., Рынок. Микроэкономическая модель. — СПб., 1992.
4. , Микроэкономика. — М.: ДИС, 1997. — Гл. 5—7.
5. Микроэкономика. — М.: Дело, 1992. — Гл. 3—4.
6. Розанова К, Основы экономического выбора. — М.: ТЕИС, 1996.
7. Суверенитет и рациональность потребителя // Теория потребитель
ского поведения и спроса. — СПб.: Экономическая школа, 1993.
8. Франк и поведение. — М.: ИНФРА-М, 2000. — Гл. 3—8.
9. Хайман микроэкономика: анализ и применение. В 2-х т. — М.:
Финансы и статистика, 1992. — Т.1. — Гл. 3—4.
10. ХиксДж. Р., Д. Пересмотр теории ценности // Теория потребительского
поведения и спроса. — СПб.: Экономическая школа, 1993.
Оптимальный объем достигается когда отношение предельных полезностей равно отношению цен.

Если 160/80 = 2, то ищем такое же соотношение:
150/2=75 (нет такой предельной полезности конфет);
120/2=60 (Есть такое значение);
90/2=45 (нет такой предельной полезности конфет);
Проверяем бюджет: 
Ответ: 1 кг. Конфет и 2 кг. Винограда.
Задание 6.Допустим, потребитель имеет доход 300 ден. ед. в месяц и он весь должен быть израсходован на покупку двух товаров: товара Х ценой 3 ден. ед. за штуку и товара Y ценой 5 ден. ед. за штуку.
Напишите уравнение бюджетной линии и отобразите в виде графика.

Задание 7. На рисунке показана одна из кривых безразличия некоего потребителя и его бюджетная линия.
а) Если цена товара Y равна 50 ден. ед. за единицу, то какой доход имеет потребитель? 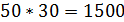
б) Какова цена товара Х? 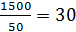
в) Написать уравнение бюджетной линии. 

г) Написать уравнение бюджетной линии при условии, что цена товара Y составляет 60 ден. ед. за единицу.




Задание 12. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии и соответствующие им кривые безразличия.
Определить координаты двух точек линии спроса данного потребителя на товар Х.
 – цена товара х.
– цена товара х.
 – цена товара y.
– цена товара y.


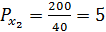
1. Что является предметом изучения теории полезности?
Степень полезности с увеличением количества потребления.
2. Какие факторы влияют на изменение положения и угла наклона бюджетной линии?
Изменение соотношения цен на блага.
Изменения дохода с учетом налоговых отчислений. Следовательно, изменение налогов тоже влияет на доход.
3. В каком случае достигается потребительское равновесие?
Потребитель получает максимальную полезность.
Практическое занятие 3. Спрос, предложение, цена, эластичность
Практическая часть 1
Задание 1.Построить модель частичного рыночного равновесия на рынке зерна, используя данные табл.1, характеризующие общий объем спроса на пшеницу и общий объем предложения пшеницы на зерновой бирже в Канзас-Сити в месяц. Обозначьте равновесную цену буквой «РЕ», а равновесное количество – буквой «QЕ».
Таблица 1. Ситуация на зерновой бирже
| Спрос, тыс.бушелей | Цена за бушель*, (дол.) | Предложение, тыс.бушелей |
| 3,40 | ||
| 3,70 | ||
| 4,00 | ||
| 4,30 | ||
| 4,60 | ||
| 4,90 |
*Бушель – (англ. bushel) — единица объёма, используемая в английской системе мер. Применяется для измерения сыпучих товаров, в основном сельскохозяйственных (ёмкость примерно на 36 л)

Проанализировав данные табл.1 и построенной модели, ответьте на следующие вопросы:
а) какова будет рыночная или равновесная цена? Каково равновесное количество пшеницы?
Равновесная цена 4,00 доллара за бушель, равновесное количество 75 т.бушелей.
б) почему цена 3,4 дол. не станет на этом рынке равновесной? Почему не станет ею и цена 4,9 дол.?
Объем спроса не равен объему предложения.
в) «Излишки повышают цены, а нехватки их понижают». Вы с этим согласны? Поясните свой ответ.
Не верно. Дефицит увеличивает цену, излишки снижают цену.
г) предположим, что правительство установило потолок цены на пшеницу в размере 3,7 дол. за бушель. Подробно объясните, какие последствия повлечет за собой такая цена? Представьте ваш ответ в графическом изображении на построенной модели. Что могло заставить правительство установить максимальный предел цены?
Избыточный спрос и недостаточное предложение приведет к перераспределению рынка альтернативных продуктов в связи с дефицитом товара. Целью правительства может служить как раз перераспределение рынка, позиционирования альтернативного продукта или снижение нагрузки на население в кризис, для получения политических выгод в ущерб рыночным.
д) допустим, что правительство установило предел цены на пшеницу – 4,6 дол. за бушель. Объясните подробно, какие последствия повлечет за собой эта гарантированная цена. Изобразите ваш ответ на графике. Что могло побудить правительство установить эту гарантированную цену?
Перераспределение рынка на более дешевую альтернативу. Увеличение предложений на начальном этапе и уменьшение поставщиков ввиду падения возможного спроса в будущем.
Задание 2.Поясните с помощью модели рыночного равновесия (графического изображения), как повлияет каждое из перечисленных ниже изменений в спросе и (или) предложении на равновесную цену и равновесное количество продукта на конкурентном рынке:
1) предложение сокращается, а спрос остается неизменным;
Увеличится равновесная цена.
2) спрос сокращается, а предложение остается неизменным;
Уменьшится равновесная цена.
3) предложение увеличивается, а спрос остается неизменным;
Уменьшится равновесная цена.
4) спрос повышается, и предложение повышается;
Равновесная цена не изменится.
5) спрос повышается, а предложение остается неизменным;
Увеличится равновесная цена.
6) предложение увеличивается, а спрос сокращается;
Резко уменьшится равновесная цена.
7) спрос сокращается, и предложение сокращается;
Равновесная цена не изменится.
8) спрос повышается, а предложение сокращается.
Резко увеличится равновесная цена.
Задание3. Предположим, что спрос на товар представлен в виде уравнения РD = 10 – 0,2Q, а предложение – уравнением РS = 2 + 0,2Q , где Q – величины спроса и предложения, а РD и РS – цена соответственно спроса и предложения. Используя условие равновесия PD = PS, определите равновесное количество. Затем определите равновесную цену. В подтверждение ваших ответов дайте графическое изображение двух уравнений.

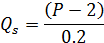
Приравниваем и решаем:

Отбрасываем знаменатель как не имеющий значения в данном случае.
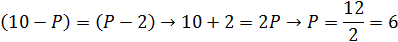


Задание 4. Функция спроса на мясо имеет следующий вид: QD = 30 – Р, а функция предложения описывается следующим уравнением: QS = 15 + 2Р, где QD и QS – величины соответственно спроса и предложения, а Р – цена. Используя условие равновесия QD = QS, найдите равновесный объем и равновесную цену на мясо и покажите графически. Какая ситуация сложится на рынке мяса (избыток товара или дефицит), если цена упадет до 3 рублей или вырастет до 20 рублей? Сложившуюся ситуацию изобразите на графике.


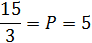
Равновесная цена 5 ед.денег Равновесный объем 25 ед.мяса
Теоретическая часть 2
Практическая часть 2
Задание 1
Функция спроса населения на данный товар QD = 9 – P, функция предложения данного товара QS = – 5 + 2P.
Предположим, что на данный товар введен налог, уплачиваемый продавцом в размере 2 ден. ед. на единицу товара.
Определите общую сумму налога, поступающего в бюджет (в ден. ед.):
1) 6; 2) 8 2 /3; 3) 10; 4) 12 2 /3; 5) 14; 6) 16 2 /3.
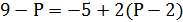



Задание 2
Функции спроса и предложения для конкретного товара имеют вид: QD = 9 – P и QS = – 2 + 2P.
Предположим, что на данный товар введен налог, уплачиваемый продавцом, в размере 2 ден. ед.
Определите, какую цену за единицу продукции реально получает продавец данного товара (в ден. ед.):
1) 3; 2) 5; 3) 7; 4) 9; 5) 1.
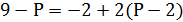
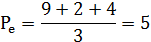
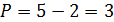
Задание 3
Спрос и предложение некоторого товара описываются уравнениями: QD = 600 – 25P и QS = 100 + 100P.
где Р – цена за единицу товара, ден. ед.
Государство установило налог с продажи на единицу данного товара в размере 2,5 ден. ед.
Определите, какую часть налоговых поступлений (в абсолютном измерении) вносят в госбюджет покупатели этого товара ( ден. ед.):
1) 800; 2) 900; 3) 1000; 4) 1100; 5) 1200; 6) 1300.
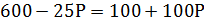

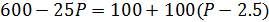
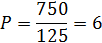

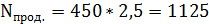
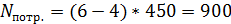
Ответ №2=900 ден.ед.
Задание 4
Функция спроса на штучный товар имеет вид: QD = 2220 – P, функция предложения: QS = 3P – 300.
Правительство ввело дотацию в 100 ден. ед., получаемую продавцом за каждую единицу продукции. Равновесная цена и равновесный объем продаж после этого составили (в ден. ед.):
1) 480; 2) 500; 3) 555; 4) 600; 5) 645.


Ответ №3=555 ден.ед.
Практическая часть 3
Задание 1.Определить коэффициент прямой эластичности спроса по цене, если известно, что при цене 20 ден. ед. объём спроса на товар 600 штук, а при цене 80 ден. ед. – 200 штук.
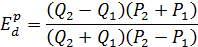


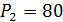
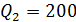
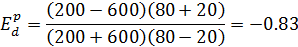
Задание 2.За определенный период времени потребитель покупает 12 кг говядины по цене 16 ден. ед. за 1 кг, а по цене 14 ден. ед. – 13 кг. Определите коэффициент эластичности и с какого рода ценовой эластичностью мы имеем дело:
[spoiler title=”источники:”]
http://pandia.ru/text/78/452/39181-3.php
http://poisk-ru.ru/s42415t3.html
[/spoiler]
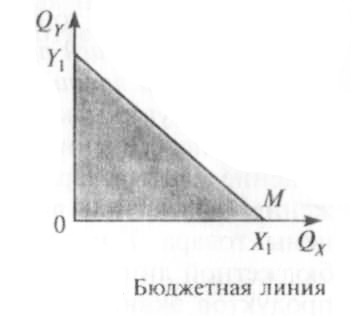
Бюджетная линия (также известная как бюджетное ограничение или бюджетная строка) – это таблица или график, которые показывают ряд различных комбинаций двух продуктов, которые могут быть потреблены при заданном доходе и ценах.
Бюджетная линия для потребителей – это то же самое, что кривая производственных возможностей для производителей. Это полезный инструмент для понимания потребительского поведения и выбора.
Бюджетная линия отображает потребительский выбор между двумя продуктами. Количество единиц одного продукта отображается по горизонтальной оси, а количество единиц другого – по вертикальной.
Каждая возможная комбинация этих двух продуктов затем строится для получения кривой бюджетных ограничений.
Бюджетная линия является ограничением в том смысле, что она ограничивает общее потенциальное потребление потребителя.
Достижимо только такое сочетание двух товаров, которое укладывается в бюджетное ограничение или входит в него. Любая комбинация двух товаров, выходящая за рамки бюджетной строки, недостижима.
Вместе с кривыми безразличия потребителя, показывающими различные комбинации двух продуктов, которые дают потребителю одну и ту же полезность, можно прийти к комбинации двух товаров, которая будет оптимальной для потребителя с точки зрения максимального удовлетворения его пожеланий.
Уравнение бюджетного ограничения
Совокупные расходы на любую комбинацию товаров по бюджетной статье равны доходам потребителей. Это можно выразить математически следующим образом:
QAPA + QBPB = I,
где QA и QB – единицы товара A и товара B, PA и PB – их соответствующие цены, а I – общий доход потребителя.
Предположим, что продукт А находится на оси Y, а продукт В – на оси X. Мы можем записать бюджетное ограничение в стандартном формате прямолинейного уравнения:
QA = I/PA – (PB/PA) × QB
Оно показывает, что наклон бюджетной линии равен отрицательному отношению цены товара по оси X к цене товара по оси Y.
Бюджетная линия смещается, когда изменяется доход потребителя: она смещается внутрь, когда доход уменьшается, и смещается наружу, когда доход увеличивается. Но когда происходит изменение цены только одного товара, бюджетная строка вращается, то есть смещается, но не параллельно.
Пример
Предположим, вы получили подарочную карту AppStore на 50 долларов от своего друга. Вы подумываете о покупке видеоигр и песен для своего смартфона. Цена игры – 5 долларов, а песни – 1 доллар.
Вы можете либо потратить всю сумму на игры, и в этом случае купленные игры будут стоить 10 [= $50 / 5]. Или вы можете потратить всю сумму на музыку, и в этом случае количество купленных песен составит 50.
Скажем, количество песен представлено вдоль горизонтальной оси X, а количество игр – вдоль вертикальной оси Y. Теперь у нас есть две точки на бюджетной линии (0,10) и (50,0).
Вышеперечисленные комбинации редко приобретаются типичным потребителем. Вы, скорее всего, купите и игры, и песни в некотором количестве выше нуля.
Допустим, вы покупаете 6 игр. Это будет 30 долларов [= 4 × 5]. На оставшуюся сумму можно купить 20 песен. Теперь у нас есть еще одна точка на графике (20,6).
Если мы построим вышеприведенные точки и любые другие возможные комбинации, которые вы можете выбрать, мы получим прямую бюджетную линию, как показано ниже:

Достижимая комбинация – это любая комбинация двух продуктов, которые могут быть приобретены с использованием данного дохода. Все пункты на или ниже бюджетной линии достижимы, например, 20 песен и 4 игры.
Недостижимая комбинация – это любая комбинация двух продуктов, которую невозможно приобрести с использованием данного дохода. Все пункты выше бюджетной линии недостижимы, например, 30 песен и 6 игр.
Бюджетная линия и ее свойства
Кривые
безразличия описывают систему предпочтений
потребителя, бюджетная линия характеризует
множество доступных потребителю
вариантов. Бюджетное
ограничение показывает,
какие потребительские наборы доступны
потребителю при данных ценах и доходе:
![]()
Рх и
Ру — цена товара Х и Y; Qx и Qу—
количества товаров X и Y; М — располагаемый
доход, т.е. сумма затрат на все блага не
превышает дохода потребителя.
Бюджетное
пространство –
вся доступная потребителю область
выбора.
![]()
Бюджетная
линия пересекает оси координат в точках
X1 = M/Px и Y1 = M/Py, показывающих
максимально возможные количества благ
X и Y, которые может приобрести потребитель
на данный доход при данных ценах.
Свойства
бюджетной линии:
1.имеет
отрицательный наклон.
Наборы благ имеют равную стоимость,
увеличение потребления одного блага
возможно только при сокращении потребления
другого.
2. Расположение
бюджетной линии зависит от величины
денежного дохода.
Увеличение денежного дохода потребителя
при неизменных ценах приводит к
параллельному перемещению бюджетной
линии вправо (рис.а). Уменьшение денежного
дохода потребителя при неизменных ценах
приводит к параллельному перемещению
бюджетной линии влево (рисб). Изменение
дохода потребителя не меняет угла
наклона бюджетной линии, но меняет
координаты точек пересечения бюджетной
линии с осями координат.
3. Коэффициент
наклона бюджетной линии равен соотношению
цен благ, взятому с противоположным
знаком.
Коэффициент наклона бюджетной линии –
отношение цены блага, отсчитываемого
по горизонтали, к цене блага, отсчитываемого
по вертикали, крутизна наклона равна
(- Px/Py). Потребитель должен воздержаться
от приобретения некоторого количества
товара X, чтобы приобрести некоторое
количество Y.
4. Изменение
цен продуктов приводит к изменению угла
наклона бюджетной линии.
Изменение цен обоих продуктов эквивалентно
изменению реального дохода потребителя
и перемешает бюджетную линию вправо
или влево
Графическая интерпретация потребительского равновесия
Бюджетная
линия несет объективную информацию о
величине дохода потребителя и ценах
на товары, показывает все доступные
потребителю комбинации благ Х и Y. Кривые
безразличия несут субъективную
информацию о предпочтениях потребителя
и строятся на основе наборов безразличия.
Совмещая бюджетную линию и карту
безразличия, можно найти оптимум
потребителя.
Точка
оптимума потребителя
не может лежать ниже бюджетной линии,
т.к. это означало бы, что часть дохода
потребителя осталась неизрасходованной.
Это противоречит допущениям ординалистской
теории потребительского поведения, в
частности первому постулату о
ненасыщаемости, что люди всегда
предпочитают большее количество данного
блага меньшему. Следовательно, точка
Е, лежащая на кривой безразличия
U1 не может быть точкой оптимума
потребителя (см. рисунок).
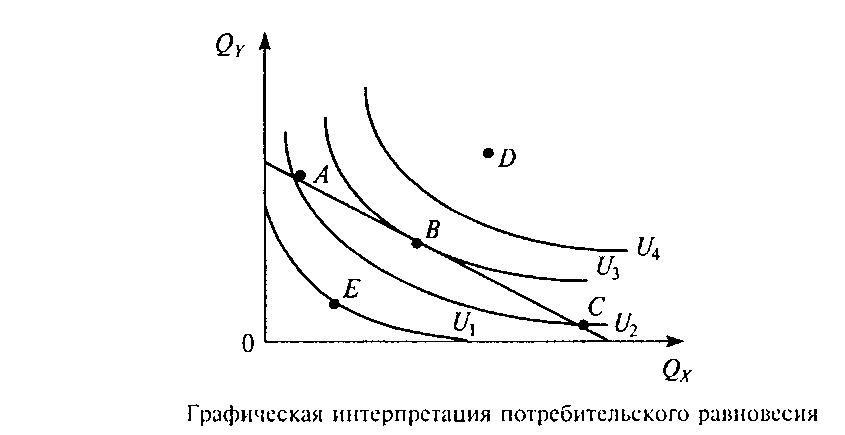
Точки
А, В и С, лежащие на бюджетной линии.
Приобретая наборы, соответствующие
этим точкам, потребитель расходует весь
свой бюджет. Однако точки А и С, лежащие
на кривой безразличия U2, не являются
точками оптимального потребительского
выбора, так как, перемещаясь по бюджетной
линии вниз от точки А и вверх от точки
С, можно перейти на кривую безразличия
U3, которая обеспечивает более высокий
уровень полезности. Точки А и С показывают
доступные данному потребителю комбинации
благ X и Y, соответствующие меньшим
совокупным полезностям, о чем
свидетельствует факт их расположения
на более низких кривых безразличия.
Комбинация благ, максимизирующая
полезность, будет соответствовать
точке, лежащей на наивысшей из доступных
потребителю кривых безразличия. Точкой
потребительского оптимума является
точка B, так как она расположена на
наиболее высоко лежащей из доступных
потребителю кривых безразличия — U3.
В
точке потребительского оптимума (В)
совпадают углы наклона бюджетной линии
(Px/Py) и кривой безразличия (MRS). Предельная
норма замещения MRS показывает, в каком
соотношении потребитель желает обменивать
блага X и У. Соотношение Px/Py демонстрирует,
в какой пропорции потребитель действительно
может обменивать эти блага, т. е. от
приобретения какого-то количества
товара X следует ему воздержаться, чтобы
получить средства, необходимые для
покупки единицы товара Y.
![]()
Потребитель
максимизирует свою полезность, если
покупает товары Х и Y таким образом, что
их предельные полезности в расчете
на денежную единицу равны. Таким образом,
в точке В достигается оптимальная
из доступных потребителю комбинация
продуктов Х и Y.
Точка
D, расположенная на наиболее высокой
кривой безразличия U4 и соответствующая
большей сумме полезности, чем точка В,
не будет являться точкой оптимума, так
как находится выше бюджетной линии и
недоступна для данного потребителя.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Maksim Maksimov
Эксперт по предмету «Экономика»
Задать вопрос автору статьи
Понятие бюджетного ограничения
Рассмотрим понятие бюджетного ограничения.
Определение 1
Бюджетное ограничение – это все комбинации товаров или благ, которые потребитель может купить при определенном доходе и ценах.
Данное понятие прямо связано с бюджетной линией, которая является графическим отображением бюджетного ограничения.
Определение 2
Бюджетная линия – это изображенная на графике прямая, все точки которой должны показывать все комбинации товаров и благ, услуг, при приобретении которых потребитель потратит свой доход полностью.
Бюджетная линия представлена на рисунке 1.
Итак, как видно на графике, если потребитель приобретет товары, услуги, то выше линии будут находиться те товары, которые являются недоступными, а ниже линии те товары, которые потребитель может приобрести на свой бюджет.
На графике Х, У – это определенные товары и услуги, которые может приобрести потребитель и цены таких товаров.
Линия, представленная на графике, показывает фиксированный доход, выше которого потребитель приобрести благ не может из-за бюджетного ограничения.
При решении задач, а также в теории, используется не только графический способ изображения и расчета бюджетного ограничения, но и числовой. То есть для определения бюджетного ограничения используется уравнение.
Рассмотрим уравнение бюджетного ограничения.
Уравнение линии бюджетного ограничения
Итак, возьмем за I полностью весь доход определенного потребителя.
За цену определенного блага примем Px для блага Х, Py для блага Y.
Таким образом, запишем уравнение следующим образом:
Замечание 1
Уравнение бюджетного ограничения $I = Pxcdot Х + Pycdot Y$
«Уравнение линии бюджетного ограничения» 👇
Если благо Х будет равно нулю, то весь доход будет потрачен на благо Y, то есть $Pycdot Y$ (цена $cdot$ количество товара);
Если благо Y будет равно нулю, то весь доход будет потрачен на благо Х, то есть $Pхcdot Х$ (цена $cdot$ количество товара);
Итак, на уравнение бюджетного ограничения влияют два главных фактора:
- цена блага;
- количество приобретаемого блага;
- выбор потребителя в пользу одного или другого блага.
Замечание 2
Обратите внимание, если доход потребителя вырастет или станет ниже, или цены благ упадут или станут выше, бюджетное ограничение также изменится. Важно, что при совмещении бюджетного ограничения и кривых безразличия возможно определить равновесие потребителя (такие расчеты важны не только на макроэкономическом уровне, но и на микроэкономическом).
Для того чтобы понять сущность бюджетного ограничения и уравнения, рассмотрим примеры расчета.
Пример расчета
Составим уравнение бюджетного ограничения при следующих условиях.
Предположим, что потребитель выбирает между двумя товарами, которые для потребителя являются взаимозаменяемыми. Общий доход потребителя составляет 2000 условных единиц. Цена продукта Х составляет 40 условных единиц, а продукта Y – 20 условных единиц.
Таким образом, уравнение бюджетного ограничения выглядит так:
$I = 40 Х + 20 Y$ (значения Х, Y могут быть различны, в зависимости от выбора потребителя в пользу одного иди другого товара, но не больше, чем 50 единиц для Х, 100 единиц для Y).
Так, если потребитель, приобретает товары в равном количестве, то уравнение выглядит так:
$I = 40cdot 25 + 20cdot 50$, то есть при доходе в 2000 условных единиц, потребитель может приобрести при условии равномерной покупки одного и второго блага, 25 единиц товара Х и 50 единиц товара Y.
Обратите внимание, что потребитель может выбрать и другие комбинации благ, полагаясь на личный выбор.
Замечание 3
Важно, что потребитель стремится к максимизации полезности от приобретения благ.
При условии максимизации полезности, для расчетов дополнительно используется уравнение максимизации полезности.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме