Формула расчета рыночной доходности
Любому, кто занимается вложением средств, необходимо уметь грамотно рассчитывать доходность — как для собственных нужд, так и для правильного прочтения различных источников, где указываются результаты инвестиций. В самом простом случае — банковского депозита — рост дохода происходит по прямой линии и сложных расчетов не требуется.
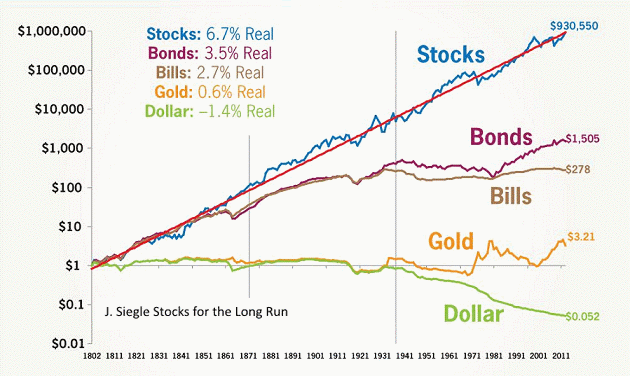
Однако если мы возьмем банковский депозит с возможностью капитализации процентов, то картина уже изменится: счет начнет расти по экспоненте. Аналогичный, но более сильный эффект дает инвестирование на фондовом рынке в акции (логарифмическая шкала):
Вообще говоря, в сети нетрудно найти калькулятор сложного процента — но подойдет он отнюдь не для каждой задачи и поскольку содержит формулу в закрытом виде, то не дает понимания о сути расчета. Непонимание работы с рыночными данными способно привести к ошибкам даже в самых простых случаях. Ниже мы рассмотрим, как посчитать доходность в процентах для разных случаев.
Например, в первый год стоимость произвольно выбранного актива увеличилась на 100%, а во второй год уменьшилась на 50%. Что будет с общей доходностью? Она будет считаться не как среднее арифметическое (25%) — а исходя из того, что в первый год она удвоилась, а во второй год в два раза упала. Следовательно, в сумме за два года оставшись на прежнем уровне.
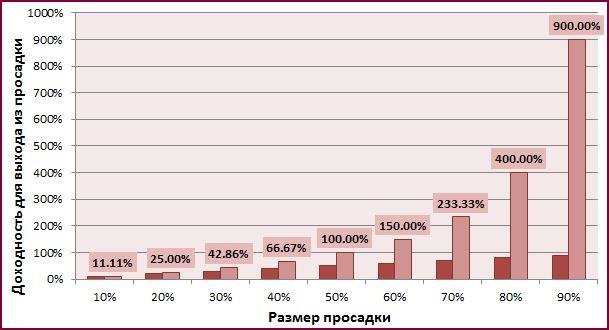
Из этого следует очень важное правило: чем выше просадка, тем большая доходность требуется, чтобы ее отыграть. К примеру, если стоимость актива за год уменьшилась на 80% (осталось только 20% начальной цены), то требуется доходность в целых 400%, чтобы достичь первоначального уровня:
Именно поэтому агрессивные стратегии с высоким кредитным плечом не живут долго — математическое ожидание даже при большей вероятности прибыли, чем убытка все равно со временем уничтожит депозит.
В общем случае формула доходности выглядит так:
A(n) = A(n-1) × (1 + X) = A(0) × (1 + X)^n или X = (A(2)/A(0))^(1/n) – 1
- A(0) – исходное количество денег
- А(n) – количество денег через n лет
- X – годовая доходность (в процентах)
Если же взять изменение за год в разах (Y) (т.е. мы рассматриваем изменение на 10% как рост в 1,1 раза, Y = 1 + 10/100 = 1,1), то
A(n) = A(n-1) × Y = A(0) × Y^n
Задача
Актив растет на 10% в год. Какова будет его доходность через 2 года?
Можно искать калькулятор сложного процента, а можно сказать, что Y = 1.1, число лет n = 2. Тогда взяв исходное количество денег за условную единицу
А(2) = 1 × 1.1² = 1.21, т.е. актив вырастет на 21% (из 1000 рублей будет 1210)
Обратная задача
Найти среднюю годовую доходность при росте актива на 21% в течение двух лет (понятно, что она может расти неравномерно — мы же найдем среднюю величину):
Y = ((A(2)/A(0))^(1/n)
Снова принимая нашу первоначальную доходность за условную единицу, считаем:
Y = (1.21/1)½ = 1.1, т.е. усредненная доходность равна 10%
Задача 2
За четыре года банковский вклад с ежегодной капитализацией прибыли вырос от 100.000 рублей до 150.000 рублей. Какова средняя доходность в годовом исчислении?
Y = (150.000/100.000)^(1/4) = 1.10668, т.е. средняя годовая доходность равна 10.67%
Соответственно, просто разделив 50% на 4 мы получили бы среднеарифметическую доходность 12.5%, что неверно. Эта разница и есть преимущество сложного процента: без него доходность каждый год начислялась бы на 100.000 рублей — т.е. каждый год мы получали бы 12.500, что за четыре года и даст ровно 50.000. Однако при ежегодной капитализации мы добиваемся того же результата уже с меньшим процентом (10.67%).
Задача 3
За 2 года и 6 месяцев стоимость пая в инвестиционном фонде выросла на 42.7% (допустим, пай стоил 5 рублей, а стал стоить 7.135 рубля — значит, 7.135/5 = 1.427). Какова средняя доходность фонда в год?
2 года и 6 месяцев это 2.5 года (n = 2.5), а Y = 1.427. Тогда
Y = (1.427/1)^(1/2.5) = 1.1528, т.е. средняя годовая доходность равна 15.28%
Если за «n» обозначить количество месяцев (n = 30), то теперь можно вычислить и среднемесячную доходность (1.427^(1/30) = 1.0119 или 1.19%. При этом среднеарифметическая доходность была бы 42.7/30 = 1.4233%). Если мы возьмем банковский депозит, где капитализация происходит ежемесячно, то считать надо в месяцах, если ежегодно — то в годах.
Задача 4
Значение индекса ММВБ на конец декабря 1997 года – 85.05 пунктов. Значение индекса ММВБ на конец 2007 года – 1888.86 пунктов. Какова среднегодовая доходность индекса ММВБ за 10 лет?
Y = (A(2)/A(0))^(1/n) = (1888.86/85.05)^(1/10) = 1.3635 или 36.35%
Задача 5
Ниже дана российская инфляция за 2000-2007 годы. Нужно рассчитать среднегодовую.
2000 г. – 20,2%
2001 г. – 18,6%
2002 г. – 15,1%
2003 г. – 12,0%
2004 г. – 11,7%
2005 г. – 10,9%
2006 г. – 9,0%
2007 г. – 11,9%
Это как раз случай, хорошо приближенный к реальности — доходность фондового рынка можно смотреть как по разнице пунктов за выбранный промежуток времени, так и считать (или брать из справочника) по годам. Тогда общий рост потребительской корзины:
1,202 × 1,186 × 1,151 × 1,120 × 1,117 × 1,109 × 1,090 × 1,119 = 2,777 раза (или на 177%)
И средняя инфляция
Y = (A(2)/A(0))^(1/n) =2.777^(1/8) = 1.1362 или 13.62%
P.S. Задача аналогично может быть использована для расчета средней доходности активов, которая за год бывает отрицательной. В этом случае коэффициент берется меньше 1, например при доходности минус 10% в год он равен 1 — 10/100 = 0.9.
Задача 6
Инвестор входит в некоторый счет, который показывает в текущий момент 1500%. Выходит из него через полгода, когда показатель достигает 1700%. Пусть он инвестировал 500 долларов и получил 70% от роста котировок. Каков его доход в % годовых и по абсолютной величине?
Это не 200%, умноженные на 0.7! Считаем: (1 + 1700/100)/(1 + 1500/100) и получаем 1.125, т.е. 12.5% за полгода. Следовательно, среднеарифметически в год будет в два раза больше, а среднегеометрически 1.125^(1/0.5) = 26.56%. Хотя такой расчет в этом случае не будет корректен — мы экстраполируем прибыль, т.е. считаем не только имеющийся, но и будущий результат.
Как видно, в этом случае среднегеометрическая доходность получается выше среднеарифметической — так что таким приемом иногда пользуются инвестиционные фонды, экстраполируя удачные квартальные результаты на целый год. Если же нужно рассчитать доход на 500 долларов за время инвестирования, то сначала учтем, что инвестор получает лишь 70% от роста, т.е. 12.5% × 0.7 = 8.75%. Следовательно, прибыль равна 500 × 8.75% / 100% = 43.75 долларов.
Похожий пример: вошли в счет на отметке доходности в 30%, вышли на 90%. При этом прибыль инвестора увеличилась не в три раза, а на (1 + 90/100)/(1 + 30/100) ≈ 1.46, т.е. примерно на 46%. Если взять 500 долларов, инвестированные в счет, то суммарный баланс составит примерно 730 долларов (прибыль около 230 $).
Задача 7
Расчет доходности акций с учетом дивидендов и курсового роста стоимости. Пусть была куплена акция одной компании за 120 рублей. Спустя какое-то время по ней получены дивиденды 7.2 рубля, а котировки выросли до 135 рублей — после чего акцию продали. Рассчитать полученный доход.
Y = [(7.2 + (135-120))/120] × 100% = 18.5%
Задача 8
По данным предыдущего примера рассчитать доходность в процентах годовых, если на момент продажи акции (достижения ее стоимости 135 рублей) прошло 250 дней:
Y = [(7.2 + (135-120))/120] × 365/250 × 100% = 27.01%
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
- Коэффициент вариации — coefficient of variation.
- Коэффициент Шарпа — Sharpe ratio.
- Коэффициент информации — information ratio.
- Коэффициент Сортино — Sortino ratio.
- Коэффициент Трейнора — Treynor ratio.
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
(Pt + 1 − Pt + CF) / Pt,
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
Бытовой пример: инвестор купил акцию за 100 $ и продал за 150 $, а за время владения получил 3 $ дивидендов. Доходность по формуле выше будет считаться так:
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
Например, акции Apple 31 декабря 2016 стоили 27,4 $, а 30 сентября 2020 — 115,6 $. Посчитаем общую доходность за этот период:
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
((1 + r1) × (1 + r2) × (1 + r3) × (1 + rn))1/n − 1,
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
Например, инвестор купил акцию компании за 100 $ и владел ею 3 года. За первый год стоимость акции выросла на 20%, во второй год — упала на 10% по отношению к прошлому периоду, а за третий год акции прибавили в цене 30%. Общая годовая доходность за эти три года будет считаться так:
((1 + 20%) × (1 − 10%) × (1 + 30%))1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
(20% − 10% + 30%) / 3
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному: акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
| Покупка | Первый год | Второй год | Третий год | Четвертый год | |
|---|---|---|---|---|---|
| Акция A | 100 $ | 140 $ (+40%) | 150 $ (+7%) | 125 $ (−17%) | 180 $ (+44%) |
| Акция B | 100 $ | 70 $ (−30%) | 120 $ (+71%) | 100 $ (−17%) | 180 $ (+80%) |
Четвертый год
180 $ (+44%)
Четвертый год
180 $ (+80%)
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Актив A:
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%)1/4 = 15,8%.
Актив B:
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%)1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность)(365 / Количество дней владения активом) − 1
Например, инвестор купил акцию компании за 100 $, держал ее 714 дней, а на 715-й день продал и получил доходность 74% за весь период владения. Общая годовая доходность за рассматриваемый период будет считаться так:
(1 + 74%)(365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива)(1 / Количество периодов) − 1
Например, инвестор купил 20 акций по 200 $ и решил удерживать их 2 года. За этот период компания каждый год выплачивала 1 $ дивидендов на акцию. На момент продажи цена акции составила 270 $. В этом случае общая годовая доходность будет такой:
((270 × 20 + 2 × 20) / 200 × 20)(1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Итак, в общем виде мы рассмотрели понятия доходности и риска. Теперь я построю диаграмму «риск-доходность», чтобы проанализировать, какие активы показывают оптимальное отношение риска к доходности. Простыми словами, по диаграмме можно понять, какой актив дает максимальную доходность на единицу риска.
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
6 крупнейших по весу компаний в портфеле Berkshire Hathaway на 30.09.2020
| Компания | Тикер | Вес актива в портфеле |
|---|---|---|
| Apple | AAPL | 47,78% |
| Bank of America | BAC | 10,63% |
| Coca-Cola | KO | 8,63% |
| American Express | AXP | 6,64% |
| Moody’s | MCO | 3,12% |
| US Bancorp | USB | 2,07% |
Вес актива в портфеле
47,78%
Вес актива в портфеле
10,63%
Вес актива в портфеле
8,63%
Вес актива в портфеле
6,64%
Вес актива в портфеле
3,12%
Вес актива в портфеле
2,07%
В расчетах для повышения точности я опираюсь на ежедневные котировки акций с 2012 по 2020 год — данные и расчеты представлены в гугл-таблице.
Еще для расчетов нам понадобится бенчмарк и безрисковая ставка. Бенчмарк — это портфель, с которым мы будем сравнивать эффективность наших активов. Обычно в качестве бенчмарка берут индекс на широкий рынок США — я взял ETF SPDR S&P 500.
Безрисковая ставка нужна для расчета показателей эффективности инвестиций: в ряде этих показателей она используется как доходность от вложения в безрисковый актив, то есть актив, риск наступления дефолта по которому стремится к нулю. Конечно, абсолютно безрисковых активов не существует, поэтому в качестве безрисковой ставки часто используют процентную ставку по государственным облигациям или определяют ее равной нулю. В качестве безрисковой ставки (RFR, risk-free rate) я взял 10-летние казначейские облигации США — 10-Year Treasury Constant Maturity Rate.
Шаги будут такие:
- Берем дневные доходности активов.
- Рассчитываем по ним среднюю годовую доходность и стандартное отклонение — как делали в разделе с расчетом риска.
- Строим карту «риск-доходность».
Показатели доходности и риска
| Компания | Тикер | Среднегодовая доходность | Стандартное отклонение |
|---|---|---|---|
| Apple | AAPL | 30,2% | 28,6% |
| Bank of America | BAC | 18,4% | 31,1% |
| Coca-Cola | KO | 10,0% | 18,3% |
| American Express | AXP | 15,0% | 29,3% |
| Moody’s | MCO | 27,1% | 27,7% |
| US Bancorp | USB | 10,8% | 26,1% |
| ETF S&P 500 | SPY | 15,5% | 16,8% |
| 10-Y Treasury Bonds | DGS10 | 2,1% | 0,0% |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Среднегодовая доходность
2,1%
Стандартное отклонение
0,0%
Теперь строим карту по данным из таблицы: данные по среднегодовой доходности откладываем по вертикали, а по стандартному отклонению (риску) — по горизонтали.
Из диаграммы выше можно сделать ряд выводов относительно соотношения доходности и риска активов, определить наиболее предпочтительные и исключить наиболее убыточные из них: например, можно сделать вывод, что акции AAPL дают большую доходность, чем BAC и AXP, но при этом риск инвестирования в AAPL ниже.
Но зачастую неочевидно, какой из активов лучше, — в таком случае на помощь приходят показатели оценки соотношения риска и доходности.
Считаем индикаторы привлекательности активов
Индикаторы привлекательности активов приводят данные из таблицы выше к одному знаменателю: мы можем посчитать конкретные показатели для каждой бумаги и сравнить их. Разберем основные показатели.
Коэффициент вариации показывает величину риска, приходящуюся на единицу доходности. Он рассчитывается по следующей формуле:
CV = σ / r̄,
где σ — стандартное отклонение доходности актива,
r̄ — среднее арифметическое доходности актива.
Коэффициент вариации применяется для сравнения активов с разными доходностями и стандартными отклонениями. Применение показателя позволяет ранжировать активы по степени их рискованности. Чем больше значение показателя, тем выше риск инвестиций.
Коэффициент вариации для рассматриваемых акций
| Тикер | Среднегодовая доходность | Стандартное отклонение | Коэффициент вариации |
|---|---|---|---|
| AAPL | 30,2% | 28,6% | 0,95 |
| MCO | 27,1% | 27,7% | 1,03 |
| SPY | 15,5% | 16,8% | 1,09 |
| BAC | 18,4% | 31,1% | 1,70 |
| KO | 10,0% | 18,3% | 1,82 |
| AXP | 15,0% | 29,3% | 1,95 |
| USB | 10,8% | 26,1% | 2,40 |
Среднегодовая доходность
30,2%
Стандартное отклонение
28,6%
Коэффициент вариации
0,95
Среднегодовая доходность
27,1%
Стандартное отклонение
27,7%
Коэффициент вариации
1,03
Среднегодовая доходность
15,5%
Стандартное отклонение
16,8%
Коэффициент вариации
1,09
Среднегодовая доходность
18,4%
Стандартное отклонение
31,1%
Коэффициент вариации
1,70
Среднегодовая доходность
10,0%
Стандартное отклонение
18,3%
Коэффициент вариации
1,82
Среднегодовая доходность
15,0%
Стандартное отклонение
29,3%
Коэффициент вариации
1,95
Среднегодовая доходность
10,8%
Стандартное отклонение
26,1%
Коэффициент вариации
2,40
Можно сделать вывод относительно того, какой из активов несет больше или меньше риска. Теперь мы видим, что инвестиции в AAPL выгоднее не только инвестиций в BAC и AXP, но и вообще в любой из рассматриваемых активов: на единицу риска тут приходится наибольшая доходность. Самый рискованный актив — USB: на 1% доходности приходится 2,4% стандартного отклонения.
Коэффициент Шарпа показывает, во сколько раз избыточная доходность от инвестирования в портфель по сравнению с безрисковым активом выше уровня риска инвестиций. Избыточная доходность показывает, насколько доходность инвестиционного портфеля выше доходности безрискового актива, в роли которого чаще всего выступают государственные облигации.
Коэффициент Шарпа определяется по следующей формуле:
R̄x − R̄f / σx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σx — стандартное отклонение доходности актива за сопоставимый период.
Рассмотрим пример. Предположим, что средняя доходность по акции составляет 30% годовых при 20% стандартного отклонения, а средняя доходность по государственным облигациям США (безрисковый актив) равна 3% годовых. Тогда коэффициент Шарпа для нашей акции будет считаться так:
(30% − 3%) / 20% = 1,35
Это значение показателя говорит о высокой инвестиционной привлекательности нашей акции: доходность по ней выше доходности безрискового актива и превышает уровень риска.
Из формулы видно, что коэффициент Шарпа измеряет вознаграждение в виде средней избыточной доходности на единицу риска. Также следует отметить, что коэффициент был создан для анализа портфелей, а не отдельных инструментов, но все же его следует учитывать при отборе активов в портфель: он позволяет сделать вывод об эффективности вложения.
Критерии эффективности инвестиций на основе коэффициента Шарпа
| Критерий | Вывод по активу |
|---|---|
| Коэффициент Шарпа > 1 | Доходность инвестиций выше доходности безрискового актива и превышает уровень риска |
| 1 > коэффициент Шарпа > 0 | Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности |
| Коэффициент Шарпа < 0 | Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив |
Коэффициент Шарпа > 1
Доходность инвестиций выше доходности безрискового актива и превышает уровень риска
1 > коэффициент Шарпа > 0
Риск инвестирования выше, чем доходность от инвестирования, — необходимо пересмотреть инвестиционное решение относительно этого актива или группы активов. Инвестирование в актив не приносит достаточной доходности
Коэффициент Шарпа < 0
Доходность от инвестирования ниже доходности безрискового актива. Вероятно, лучше инвестировать в безрисковый актив
Рассмотрим результаты расчетов по коэффициенту Шарпа для акций в нашем примере.
Коэффициент Шарпа у акций из портфеля Баффетта
| AAPL | 0,98 |
| MCO | 0,90 |
| SPY | 0,79 |
| BAC | 0,52 |
| AXP | 0,44 |
| KO | 0,43 |
| USB | 0,33 |
Коэффициент информации характеризует соотношение риска-доходности актива или портфеля по сравнению с бенчмарком. Коэффициент расчетами напоминает коэффициент Шарпа, только вместо безрисковой ставки используется определенный эталон — бенчмарк. Бенчмарком могут выступать широкие рыночные индексы — MSCI, S&P 500, отраслевые индексы — DJA, собственноручно разработанные бенчмарки и так далее.
Иными словами, коэффициент информации — это отношение сверхдоходности к стандартному отклонению этой сверхдоходности у актива и бенчмарка. Коэффициент помогает понять, выгодно ли инвестировать в актив или набор активов — или проще и безопасней инвестировать в актив, выбранный бенчмарком. В нашем случае в качестве бенчмарка мы взяли ETF на S&P 500.
Формула выглядит так:
R̄x − R̄m / σx − m,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄m — средняя доходность бенчмарка за сопоставимый период,
σx − m — стандартное отклонение разности доходности актива и бенчмарка за сопоставимый период.
На примере AAPL и S&P 500 все будет выглядеть так:
В числителе: считаем разницу между средней доходностью акции AAPL (30,2% годовых) и средней доходностью индекса S&P 500 (15,5% годовых).
В знаменателе: сначала считаем разницу между дневными доходностями акции AAPL и индекса S&P 500, а потом по полученной совокупности дневных сверхдоходностей определяем стандартное отклонение и приводим дневное значение стандартного отклонения к годовому, перемножив дневное стандартное отклонение на корень из 252. Перемножаем на 252, так как в году 252 торговых дня. В нашей таблице этот расчет произведен на листе «Дневная доходность».
Итого получается:
(30,2% − 15,5%) / 21,28% = 0,69. Значение показателя выше 0,5 говорит о хорошей инвестиционной привлекательности акции.
Следует отметить, что этот коэффициент показывает эффективность активного управления, — при пассивном управлении, если мы просто покупаем индексный фонд и держим его, коэффициент будет равен нулю.
Чем больше значение коэффициента, тем выше избыточная «отдача» от инвестирования в определенный актив или портфель по сравнению с бенчмарком. Значение коэффициента информации в диапазоне от 0,5 до 0,74 считается хорошим, значение от 0,75 до 0,99 считается очень хорошим, а значение свыше 0,99 считается отличным. Ниже представлены результаты расчетов коэффициента информации для рассматриваемых акций.
Коэффициент информации у рассматриваемых акций
| AAPL | 0,69 |
| MCO | 0,63 |
| BAC | 0,13 |
| SPY | 0 |
| AXP | −0,02 |
| KO | −0,36 |
| USB | −0,26 |
Можно заметить, что для SPY (ETF на S&P 500) коэффициент информации равен нулю, так как он отражает движение рынка и не подразумевает сверхдоходности за активное управление. Напротив, хорошее значение коэффициента имеют акции AAPL и MCO, у которых на 1% стандартного отклонения сверхдоходности приходится 0,69 и 0,63% сверхдоходности соответственно. В случае с KO, AXP и USB отрицательные значения коэффициента связаны с отрицательными избыточными доходностями относительно бенчмарка.
Коэффициент Сортино — показатель, напоминающий коэффициент Шарпа, он отличается лишь расчетом риска. В коэффициенте Сортино для расчета риска учитываются только доходности актива ниже определенного уровня — чаще всего этот уровень определяется как доходность безрискового актива за сопоставимый период либо нулевая ставка.
Предполагается, что положительные отклонения доходностей — выше доходности безрискового актива — не несут риск, так как повышают доходность актива, — соответственно, учитывать их при расчете риска не нужно. Таким образом, для расчета стандартного отклонения необходимо выбрать только те дневные доходности, значение которых будет ниже доходности безрискового актива за этот же день. В нашей таблице все посчитано на листе «Кф. Сортино». Вот по какой формуле этот коэффициент рассчитывается:
R̄x − R̄f / σxd,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
σxd — стандартное отклонение доходности актива ниже заданного уровня.
Для примера рассмотрим логику, по которой фильтруются доходности для расчета риска по коэффициенту Сортино.
Месячные доходности акции и безрискового актива
| Период | Доходность акции | Доходность безрискового актива | Отфильтрованная доходность |
|---|---|---|---|
| 1 месяц | 0,16% | 0,18% | 0,16% |
| 2 месяц | −2,54% | 0,18% | −2,54% |
| 3 месяц | 0,29% | 0,18% | 0,00% |
| 4 месяц | 0,00% | 0,18% | 0,00% |
| 5 месяц | 2,24% | 0,18% | 0,00% |
| 6 месяц | −11,80% | 0,18% | −11,80% |
| 7 месяц | 14,10% | 0,18% | 0,00% |
| 8 месяц | 8,36% | 0,18% | 0,00% |
| 9 месяц | −2,14% | 0,18% | −2,14% |
| 10 месяц | 9,67% | 0,18% | 0,00% |
| 11 месяц | 7,00% | 0,18% | 0,00% |
| 12 месяц | 0,90% | 0,18% | 0,00% |
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,16%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,54%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−11,80%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
−2,14%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
Доходность безрискового актива
0,18%
Отфильтрованная доходность
0,00%
В последней колонке оказались лишь те значения доходности акции, которые были ниже доходности безрискового актива за соответствующий период. Затем с помощью формулы стандартного отклонения рассчитываем риск по отфильтрованной доходности — он составит 3,54%. Среднемесячная доходность по акции — 2,19%, а среднемесячная доходность по безрисковому активу — 0,18%. Таким образом, коэффициент Сортино для акции из примера считается так:
(2,19% − 0,18%) / 3,54% = 0,57. Значение показателя ниже единицы указывает на то, что актив не обеспечивает должного уровня доходности на единицу нисходящего риска.
Чем больше значение коэффициента, тем выше вероятность безубыточности вложения и тем большей инвестиционной привлекательностью обладает рассматриваемый актив. Минимально допустимое значение показателя, определяющее инвестиционную привлекательность актива, — 1. Таким образом, на примере портфеля Баффетта допустимая и большая привлекательность у AAPL, MCO и SPY, а остальные же активы по коэффициенту Сортино непривлекательны, потому что не обеспечивают должного уровня доходности на единицу нисходящего риска.
Коэффициент Сортино у рассматриваемых акций
| AAPL | 1,59 |
| MCO | 1,40 |
| SPY | 1,19 |
| BAC | 0,86 |
| AXP | 0,73 |
| KO | 0,66 |
| USB | 0,53 |
Коэффициент Трейнора — еще один показатель, напоминающий коэффициент Шарпа и отличающийся только расчетом риска. В качестве риска берется коэффициент бета акции — он отражает волатильность актива по отношению к рынку. Коэффициент Трейнора показывает отношение сверхдоходности к рыночному риску.
Для расчета коэффициента бета акции используется следующая формула — рассчитанную бета акции можно найти на Yahoo Finance в разделе Summary на странице акции:
где σxm — ковариация между доходностью актива (портфеля) и доходностью рынка,
σm2 — дисперсия доходности рынка.
Методика расчета коэффициента бета акции раскрыта на листе «Дневная доходность» нашей таблицы, в столбце «Рыночный риск».
Коэффициент бета, находящийся в диапазоне от 0 до 1, свидетельствует о том, что акция движется в целом в одном направлении с рынком: если фондовый индекс растет, то растет и акция. Но значение коэффициента меньше 1 говорит о том, что актив менее чувствителен к движению рынка.
Коэффициент бета, равный 1, говорит о том, что движение актива полностью повторяет движение фондового индекса. Можно заметить, что значение 1 наблюдается у SPY, то есть у рыночного индекса.
Коэффициент бета больше 1 говорит о том, что динамика акции коррелирует с движением индекса, но при этом акция более чувствительно реагирует на любое движение рыночного индекса.
Коэффициент бета у рассматриваемых акций
| BAC | 1,38 |
| MCO | 1,26 |
| AXP | 1,26 |
| AAPL | 1,14 |
| SPY | 1,00 |
| USB | 1,15 |
| KO | 0,69 |
Зная коэффициент бета, доходность актива и доходность безрискового актива, мы можем рассчитать коэффициент Трейнора по следующей формуле:
R̄x − R̄f / βx,
где R̄x — средняя доходность актива (среднемесячная, среднегодовая и так далее),
R̄f — средняя доходность безрискового актива за сопоставимый период,
βx — коэффициент бета актива.
Допустим, необходимо рассчитать коэффициент Трейнора для акции USB — US Bancorp. Переходим на страницу компании на Yahoo Finance и находим Beta — 1,14 на момент написания статьи. Далее для расчета коэффициента Трейнора достаточно найти разницу между среднегодовой доходностью акции — 10,8% и среднегодовой доходностью безрискового актива — 2,1% и поделить полученное значение на бета акции.
Для акции USB:
(10,8% − 2,1%) / 1,14 = 0,076
Значение показателя выше нуля указывает на то, что инвестирование в актив более привлекательно, чем в рыночный индекс. Если коэффициент ниже нуля, то целесообразнее вкладывать в рыночный индекс, так как актив проигрывает рынку по соотношению риска и доходности. Таким образом, все акции портфеля инвестиционно привлекательны по этому показателю.
Коэффициент Трейнора у рассматриваемых акций
| AAPL | 0,24 |
| MCO | 0,20 |
| SPY | 0,13 |
| BAC | 0,12 |
| KO | 0,11 |
| AXP | 0,10 |
| USB | 0,08 |
Выводы
Теперь мы можем собрать сводную таблицу и оценить инвестиционную привлекательность активов на примере акций из портфеля Баффетта.
По данным из таблицы можно сделать вывод, что из рассмотренных активов наиболее привлекательны для инвестора Apple (AAPL), Moody’s (MCO) и SPDR S&P 500 (SPY).
Но важно помнить: кроме расчета индикаторов нужно оценивать перспективы отрасли и самой компании — и только когда картина собрана целиком, можно решать, инвестировать ли в компанию.
- Что такое доходность акций
- Виды доходности
- Дивидендная
- Рыночная
- Полная
- Годовая
- Что влияет на доходность акций
Что такое доходность акций
Доходность — это оценка эффективности вложений. С ее помощью инвестор понимает, сколько актив приносит или отнимает денег. На прибыльность влияют рост текущей стоимости акций и дивиденды.
Доходность ценных бумаг оценивают относительно некоторой базы. Обычно это первоначальная сумма инвестиций. Показатель бывает не только положительным, но и отрицательным, если стоимость актива падает.
Показатель можно рассчитать за предыдущий период. Инвесторы делают это, чтобы понять устойчивость акций в кризисы, а также их динамику в период роста фондового рынка. Также такой анализ позволяет оценить среднюю прибыльность актива.
Инвесторы прогнозируют будущую доходность. Она учитывает, например, потенциальный рост прибыли компании, а значит — увеличение размера дивидендов.
Помните, что любая прибыль по всем акциям за календарный год облагается налогами. В Российской Федерации для физических лиц — резидентов это 13% или 15%, для юридических лиц — резидентов — до 20%. Нерезиденты платят 30%. Обычно налоги удерживает брокер.
Вкладывая в акции, можно потерять часть капитала. С банковским вкладом такое невозможно. Совкомбанк не только сохранит ваши накопления, но и приумножит их.
Заставьте свои сбережения работать и приносить вам пассивный доход! В Совкомбанке есть линейка вкладов с гибкими условиями — вы сможете подобрать подходящий вариант. Высокая ставка убережет деньги от инфляции и поможет быстрее накопить на крупные покупки. Подайте заявку онлайн!
Виды доходности
Доход от акций определяют по-разному.
Дивидендная
Это отношение дивидендной выплаты к текущей стоимости акций. Формула:
дивиденд/текущая стоимость акции × 100% = дивидендная доходность
Показатель рассчитывают на дату выплаты дивидендов, ведь с момента их объявления до реального платежа проходят недели или даже месяцы.
Лаврентий купил акцию за 250 рублей 1 сентября 2022 года. 10 февраля 2023 года компания объявила о дивидендах в размере 12 рублей на акцию. К моменту выплаты – 25 февраля 2023 года – стоимость акции составляла уже 300 рублей. Таким образом, с учетом формулы 12/300 × 100%, дивидендная доходность для Лаврентия составила 4%.
У большинства компаний на бирже есть своя дивидендная политика. На нее смотрят инвесторы, чтобы определить будущую возможную прибыль.
Обычно компании отправляют на выплаты дивидендов не менее половины от чистой прибыли. Периодичность выплат устанавливают на уровне раз в квартал или полгода, реже — раз в год или месяц.
В кризис компания может перестать платить дивиденды, чтобы направить эти деньги на борьбу с его последствиями.
Например, Центробанк рекомендовал кредитным организациям не платить дивиденды в 2022 году.
При выборе дивидендных акций придерживайтесь простого правила: прибыльность должна быть выше, чем уровень ключевой ставки центрального банка и инфляции. Также я оцениваю предыдущие выплаты дивидендов компании.
Здесь обратите внимание на дивидендных аристократов, которые не просто платят на протяжении десятилетий, но и увеличивают размеры выплат.
К таким компаниям в США относятся: IBM, Exxon Mobil, Chevron.
Кто такие брокеры, и как они работают
Рыночная
Доход от акций можно оценивать не только по дивидендам, но и по изменению цены актива. При расчетах используют следующую формулу:
(стоимость продажи – стоимость покупки)/ стоимость покупки × 100%= текущая доходность
Лаврентий купил акцию маркетплейса по цене 100 000 рублей за штуку. Спустя год ее стоимость выросла до 150 000 рублей, он решил ее продать. Используем формулу (150 000 – 100 000)/ 100 000 рублей × 100% = 50% рыночной доходности до вычета налогов.
Рыночная доходность бывает отрицательной, если стоимость актива падает. Это происходит в кризисы, либо если предприятие выдает слабую отчетность.
Высокую рыночную доходность можно получить, если вкладывать деньги в акции роста. Обычно это небольшие компании из перспективных сфер (медицина, информационные технологии, зеленая энергетика). Они могут не показывать прибыли, не выплачивать дивиденды, но за счет будущих перспектив инвесторы их активно скупают.
Наибольший спрос на акции роста есть в периоды снижения ключевых ставок центральными банками.
Показателен пример с Tesla. 10 июня 2020 года, когда Федеральная резервная система США снижала ставку и стимулировала экономику во время коронакризиса, цена акций производителя электрокаров превысила 1000$. 3 января 2023 года, когда ФРС активно повышала ставку в борьбе с инфляцией, стоимость Tesla опустилась до 109,03$.
Поэтому важно смотреть не только на идею и перспективы бизнеса, но и текущую рыночную ситуацию.
Успех на фондовом рынке зависит не только от выбора активов, но и от брокера.
Чтобы успешно торговать на бирже, откройте счет у надежного брокера — «Совкомбанк Инвестиции». Вы получите широкий выбор инструментов, включая акции, облигации, фонды, а еще выгодные условия обслуживания. Оставьте заявку на свой брокерский счет онлайн.
Оставить заявку
Полная
Неправильно рассчитывать прибыльность только по изменению цены акции или дивидендам. Поэтому инвесторы используют полную доходность, чтобы учесть и дивиденды, и рост рыночной стоимости. Формула следующая:
(дивиденды + (стоимость продажи – стоимость покупки)) / стоимость покупки × 100% = полная доходность.
Лаврентий купил акции металлургического комбината за 300 рублей. За год их стоимость увеличилась до 400 рублей. А еще Лаврентий получил дивиденды — 40 рублей. Общая прибыльность до вычета налогов составила 40 + 100/ 300 × 100% = 30% до вычета налогов.
Годовая
Некоторые инвесторы хотят рассчитать годовую доходность по ценным бумагам. Так проще оценить привлекательность актива. Формула следующая:
(дивиденды +(стоимость продажи – стоимость покупки))/ стоимость покупки × количество дней в году/ количество дней владения × 100% = годовая доходность
Лаврентий купил акции автопроизводителя за 150 рублей, через полгода цена выросла до 200 рублей. Дивиденды компания за полгода не выплатила. Чтобы посчитать годовую доходность, используем формулу (200 – 150)/150 х 365/180 х 100% = 67,6%. Прибыль на акцию составила 67,6% годовых до вычета налогов.
Выделяют также конечную доходность актива, однако ее мало что отличает от расчета полной доходности. В формуле учитывают среднее арифметическое для дивидендов и годы владения активом, однако это лишь усложнение базовой формулы.
Как вывести деньги с брокерского счета
Что влияет на доходность акций
Прибыльность акций зависит от множества обстоятельств. Часть из них, например, смягчение денежно-кредитной политики, инфляцию, состояние рынка труда, динамику ВВП можно прогнозировать. Часть факторов, среди которых введение ограничительных мер, девальвация национальной валюты, повышение корпоративных налогов, прогнозы давать трудно.
В любом случае перед покупкой акций проводите фундаментальный и технический анализ. Придерживайтесь нескольких правил.
Ищите прибыльность выше уровня инфляции. Покупать акции, находящиеся в «боковике», при высокой инфляции — бессмысленно.
Покупайте инструменты, которые понимаете. Не стоит инвестировать в незнакомые вам юрисдикции только потому, что кто-то пообещал двузначную прибыль.
Диверсифицируйте вложения. Можно сочетать «голубые» фишки и акции роста. Также распределяйте инвестиции по отраслям экономики и странам. Возможно, прибыльность акций в таком случае будет ниже, но вы снизите риски.
Приведенные формулы позволят самостоятельно рассчитать доходность акций. Такая оценка поможет понять, что делать с активом прямо сейчас: покупать, держать или продавать. Инвестируйте ответственно и у надежного брокера.
Фактический доход зависит от нескольких факторов.
С 1926 года средняя годовая доходность фондового рынка составляла примерно 10%. По этой причине он считается эталоном при оценке и нацеливании на результативность долгосрочных вложений в акционерный капитал.
Является ли эмпирическое правило 10% хорошим критерием для вашего собственного портфеля, зависит от множества факторов, включая вашу терпимость к риску, временной горизонт и многое другое.
Что можно сказать о средней доходности фондового рынка?
Средняя доходность фондового рынка за почти столетие составила 10%. В результате инвесторы часто используют это как практическое правило, чтобы определить, сколько их собственных инвестиций может составить в будущем или сколько им нужно сэкономить для достижения инвестиционной цели.
Откуда взялось это правило?
Эмпирическое правило 10% отражает среднегодовую историческую доходность фондового рынка, которая обычно измеряется показателями индекса S&P 500. Этот индекс отслеживает результаты деятельности 500 крупнейших компаний США в 11 секторах и отражает состояние рынка в целом. Поскольку S&P 500 не был представлен до 1957 года, до этого использовался индекс Standard and Poor’s 90.
Как использовать среднюю доходность фондового рынка
Поскольку правило 10% основано на данных за десятилетия, оно включает в себя много лет, когда фондовый рынок возвращал менее 10% (а также многие годы, когда он возвращал больше). Вот почему его следует использовать только для целей долгосрочного планирования, таких как получение пассивного дохода или образование вашего ребенка. С его помощью вы можете спрогнозировать, сколько могут составить первоначальные и последующие инвестиции, а также сколько вам нужно ежегодно экономить, чтобы накопить целевую сумму.
Но есть несколько факторов, которые могут повлиять на вашу прибыль. Возможно, наиболее важным является ваш выбор инвестиций, на который будет влиять ваш временной горизонт и устойчивость к риску. Плата за комиссии брокеру и налоги также повлияют на вашу среднюю доходность, в то время как инфляция снизит вашу покупательную способность и, таким образом, снизит вашу эффективную доходность.
Временной горизонт
Среднегодовая доходность фондового рынка в размере 10% основана на данных за несколько десятилетий, поэтому, если вы планируете выйти на пассивный доход через 20–30 лет, это разумная отправная точка.
Но если ваш временной горизонт намного короче – скажем, вы выйдете на пенсию в ближайшие пять лет – вам следует скорректировать свои ожидания (и распределение активов в вашем портфеле).
Это связано с тем, что краткосрочная доходность фондового рынка редко совпадает с долгосрочными средними показателями. Например, в 2008 году из-за финансового кризиса S&P 500 упал на 39%. В следующем году он вырос на 30%. Фактически, если бы вы инвестировали в S&P 500 в течение пяти лет с начала 2004 по 2008 год, ваш портфель потерял бы 2,26% в годовом исчислении.
Контрольный показатель 10% не следует использовать для достижения более срочных финансовых целей с более короткими сроками, таких как #сбережения на машину или отпуск.
Вот почему эмпирическое правило 10% не работает для более коротких временных горизонтов. Если вы не будете инвестировать в долгосрочной перспективе, лучше выбрать менее волатильные (менее подверженные колебаниям рынка) и более консервативные инвестиции, чтобы гарантировать, что они будут там, когда они вам понадобятся, что обычно означает более низкие долгосрочные #инвестиции. срок возврата.
Толерантность к риску
Хотя то, как долго вы будете инвестировать, влияет на распределение активов вашего портфеля, также влияет ваша терпимость к риску или то, насколько хорошо вы можете «справиться» с большими прибылями и убытками. Это связано с тем, что получение долгосрочной выгоды зависит от того, чтобы оставаться на рынке, несмотря на взлеты и падения, в долгосрочной перспективе. Другими словами, не реагировать слишком остро и не продавать, когда вы теряете деньги, а затем пытаться вовремя вернуться.
«Купи и держи» в этом контексте не означает, что вы не можете перераспределить свой портфель по мере необходимости. Скорее, это означает, что вы продолжаете инвестировать в рынок, несмотря на взлеты и падения.
Чем выше ваша терпимость к риску, тем легче вам будет выдерживать резкие колебания рынка и сопротивляться желанию продать. Снижение риска портфеля может быть достигнуто путем добавления инвестиций с фиксированным доходом в ваш портфель, таких как #облигации и #фонды облигаций, #доллары, #золото. Но если вы добавляете в свой портфель инвестиции с фиксированным доходом, вам необходимо снизить свои ожидания относительно ожидаемой прибыли. Например, «сбалансированный» #портфель, состоящий из 50% акций и 50% фиксированного дохода, с 1926 года имел среднегодовую доходность 8,3%
Сроки рынка влияют на вашу прибыль
Ваш доход зависит от того, когда вы попадаете в акции или фонд и как долго вы инвестируете.
Например, предположим, что вы агрессивный инвестор с высокой толерантностью к риску.
Предположим, вы хотите вложить средства в фонд, который отслеживает индекс MSCI Emerging Markets Index, в который входят 27 крупных и средних компаний из 27 стран с формирующимся рынком. Если фонд, в котором вы участвуете, в точности отражает его, и вы попали в него в 2009 году, вы бы увидели среднегодовую прибыль в размере 12,35% до 2020 года (без учета комиссий за управление). Но вместо этого предположим, что вы вложились в 2011 году. Тогда ваша средняя годовая доходность была бы меньше половины этого показателя при 5,07%.
Инфляция съедает вашу прибыль
#Инфляция повлияет на покупательную способность ваших доходов. Со временем то, что вы можете купить за 100 рублей будет меньше, чем сегодня. Например, если вы скорректируете доходность фондового рынка 10% на уровень инфляции 3%, реальная норма доходности фактически составит 7%.
Неопределенность может привести к принятию более консервативных инвестиционных решений
Кроме того, важно помнить старую пословицу о том, что прошлые успехи не гарантируют будущих результатов.
Консервативный подход может потребовать более высоких взносов, но он может предотвратить дефицит, если рынок не соответствует своим прошлым доходам.
Выводы
- Фондовый рынок возвращал среднегодовую ставку 10% за почти 100 лет.
- Вы можете использовать это среднее значение, чтобы оценить, сколько вложить в акции для достижения долгосрочных финансовых целей, а также сколько ваших текущих сбережений могут составить в будущем.
- Историческая доходность – это только отправная точка. Вам необходимо учитывать другие факторы, включая ваши инвестиции и вашу терпимость к риску, продолжительность вашего инвестирования, инфляцию и налоги.
- Прошлые показатели не гарантируют будущих результатов.
Если статья была для вас полезной – подержите лайком и подпиской! 🙂 До новых встреч!
Читайте также:
Кэти Вуд – лучший инвестор, о которой мало кто слышал
5 финансовых формул, которые помогут добиться успеха
Инвестирование в акции роста: как находить акции роста
3 способа преуспеть в роли ленивого инвестора
Премия за рыночный риск (Rm – Rf) показывает величину, на которую среднерыночные ставки доходности на фондовом рынке превышали ставку дохода по безрисковым ценным бумагам в течение длительного времени. Она рассчитывается на основе статистических данных о рыночных премиях за продолжительный период. По данным агентства Ibbotson Associates, размер долгосрочной ожидаемой рыночной премии, базирующийся на данных о разнице между среднеарифметическими доходами на фондовом рынке и доходностью безрисковых инвестиций в США с 1926 по 2000 г., составляет 7,76%. Это значение могут использовать для расчетов и российские компании (в ряде учебников премия за рыночный риск принимается равной 5%).
Модель САРМ позволяет определять стоимость акционерного капитала на основе учета доходности по безрисковым вложениям и премии за риск на основе учета имеющейся доступной информации, в том числе и рыночной, что особенно важно для закрытых организаций, например банка.
В российской практике данная модель используется пока редко. Основными причинами являются:
- не сложилось значение безрисковой ставки доходности, которую в международной практике рассчитывают с доходностью 30-летних казначейских векселей Правительства. Можно взять за основу ставку доходности по облигациям внутреннего валютного займа со сроком погашения в 2010 г. В России в качестве таких активов можно рассматривать российские еврооблигации Russia-30 со сроком погашения 30 лет. Информацию о доходности этих ценных бумаг можно найти во многих финансово-экономических изданиях, например в газетах “Ведомости”, “The Moscow Times”, “Коммерсантъ”. Так, на середину февраля 2003 года ставка доходности по этим бумагам составляла 8,5% годовых;
- акции российских банков в основном не котируются на рынке, что не позволяет определить объективно среднерыночную доходность обыкновенных акций кредитных организаций (можно принять за основу фондовый индекс, устанавливаемый на российских биржах);
- субъективность расчета β-коэффициента при оценке риска конкретной организации на основе среднерыночной цены акций организации.
Пример 18. Рассчитаем ставку дисконтирования с применением модели САРМ для ОАО”ХХХ”, учитывая текущие условия, сложившиеся в российской экономике. При расчетах будем использовать следующие данные:
Rf = 8,5%
(ставка по российским европейским облигациям),
β = 1,15,
(Rm – Rf) = 7,58%.
Таким образом, доходность собственного капитала равна:
D = Rt = Rf + β * (Rm – Rf) = 8,5 + 1,15 * 7,58 = 23,28.
Такой уровень доходности следует ожидать от акций ОАО “ХХХ”. Если акция за анализируемый период не достигнет 23,28%, то такая акция является переоцененной, так как она не позволит получить необходимую компенсацию за рыночный риск, который выше среднерыночного для данного вида акций.
В зависимости от конкретных ситуаций используются различные методы расчета β-коэффициента.
Пример 19. Используя статистические данные о средней доходности операций на рынке капитала и доходности обыкновенных акций предприятия ( 16.28табл.), рассчитать коэффициент чувствительности доходности ценных бумаг ОАО “ААА” на рынке капитала. Какой уровень доходности должен быть от акций ОАО, если учитывать, что номинальная ставка дохода составит 4%, а премия за рыночный риск – 6%.
| Ситуации рынка капитала | Сколько раз наблюдалась ситуация | Средняя доходность операций на рынке,% | Доходность обыкновенных акций, % |
|---|---|---|---|
| 1 | 10 | 30 | 42 |
| 2 | 15 | 25 | 35 |
| 3 | 20 | 20 | 30 |
| 4 | 30 | 15 | 25 |
| 5 | 35 | 10 | 15 |
| 110 |
Решение:
Для решения задачи необходимо рассчитать ставку дисконта:
D = Rt = Rf + β * (Rm – Rf).
Исходя из условия задачи Rf = 4%, премия за рыночный риск (Rm – Rf) = 6%
Рассчитаем значение коэффициента β, который отражает чувствительность доходности ценных бумаг конкретной компании (Rk) на рынке капитала. Расчет коэффициента будем осуществлять в следующей последовательности.
- Рассчитаем вероятность частоты каждой ситуации, используя данные табл. 16.21, по формуле:
Рк = Мк : ∑М,
где Мк – количество наблюдений к-ой ситуации.
Результаты расчетов представлены в столбце 2 табл. 16.29.
- Рассчитаем вероятностную доходность операций на рынке по каждой ситуации, умножая вероятность ситуации на среднюю доходность операции:
ВДХк = Рк * ДХк.
Результаты расчетов представлены в столбце 3 табл. 16.29. Суммарное значение по столбцу 3 характеризует ожидаемую среднюю доходность операций на рынке (СВДХ). Среднее значение вероятной доходности по операциям на финансовом рынке составило:
СВДХ = 17,045%.
- Рассчитаем среднюю ожидаемую доходность обыкновенных акций компании, умножая вероятность ситуации на доходность обыкновенных акций компании:
ВДАКк = Рк * ДАК.
Результаты расчетов представлены в столбце 4 табл. 16.29. Просуммируем значения столбца 4, получим среднее значение ожидаемой доходности акций компании. Вероятное среднее значение доходности акций компании составило:
СДАК = 24,68%.
- Рассчитаем по каждой ситуации дисперсию (квадрат отклонения средней доходности операций на рынке от средней ожидаемой доходности на рынке, умноженный на вероятность ситуации):
Dk = (ДХк – СВДХ)2 * Рк.
Результаты расчетов записаны в столбец 5 табл. 16.29. Суммарное значение характеризует вариацию доходности рыночного портфеля:
Квд = 42,4084.
- Рассчитаем взаимное изменение среднерыночной доходности финансовых операций и средней доходности акций на рынке, используя формулу:
Р(ДО, ДАК) = (ДХк – СВДХ) * (ДАКк – СДАК) * Рк.
Результаты расчетов записаны в столбце 6 табл. 16.29. Суммарное значение представляет собой коэффициент ковариации доходности акций предприятия и рыночного портфеля:
Кков = 55,965.
- Рассчитаем уровень риска компании:
Рр = Кков : Квд = 55,965 : 42,4084 = 1,3196678 > 1.
В соответствии с таблицей степени риска β ( табл. 16.27), риск вложения денежных средств в акции данного предприятия, выше среднерыночного.
- Определим значение ставки дисконта:
D = Rf + β
* (Rm – Rf) = 4 + 1,32
* 6 = 11,92%.
Таким образом, вкладывать средства в акции ОАО “ААА” можно лишь в том случае, если на каждый вложенный рубль будет приходиться не менее 12 коп. чистой прибыли.
| № | Вероятность ситуации, Рк | ВДХ, % | ВДАК, % | Dk = (ВДХк – СВДХ) 2 *Рк | (ДХк – СВДХ) *(ДАК – СДАК) *Рк |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 10 : 110 = 0,0909 | 2,727 | 3,8178 | (30 – 17,05)2 * 0,0909 = 15,2442 | (30 – 17,05) * (42 – 24,68) * 0,0909 = 20,3883 |
| 2 | 15 : 110 = 0,1364 | 3,41 | 4,774 | (25 – 17,05)2 * 0,1364 = 8,6208 | (25 – 17,05) * (35 – 24,68) * 0,1364 = 11,1908 |
| 3 | 20 : 110 = 0,1818 | 3,636 | 5,454 | (20 – 17,05)2 * 0,1818 = 1,5821 | (20 – 17,05) * (30 – 24,68) * 0,1818 = 2,8532 |
| 4 | 30 : 110 = 0,2727 | 4,0905 | 6,8175 | (15 – 17,05)2 * 0,2727 = 1,146 | (15 – 17,05) * (25 – 24,68) * 0,2727 = -0,1789 |
| 5 | 35 : 110 = 0,3182 | 3,182 | 3,8184 | (10 – 17,05)2 * 0,3182 = 15,8153 | (10 – 17,05) * (15 – 24,68) * 0,3182 = 21,7152 |
| ∑ | 1 | 17,0455 | 24,6817 | 42,4084 | 55,969 |
Пример 20. Используя данные о структуре источников финансирования сравнимых компаний-аналогов, рассчитать b-коэффициент для ОАО “ВВВ”. Исходные данные приведены в табл. 16.30.
Какой уровень доходности должен быть от акций ОАО, если учитывать, что номинальная ставка дохода для инвестора должна составить 8%, а премия за рыночный риск – 5%?
| Исходные данные для оценки риска ОАО “ВВВ” | Расчетные данные | ||||
|---|---|---|---|---|---|
| наименование компаний | величина собственного капитала, тыс. руб. | величина заемного капитала, тыс. руб. | β-коэффициенты сравнимых компаний, β | коэффициент автономии, Кав | коэффициент Х = β * Кав |
| 1 | 2 | 3 | 4 | 5 | 6 |
| ААА | 28 000 | 25 000 | 1,13 | 0,5283 | 0,597 |
| ААВ | 35 000 | 31 800 | 1,62 | 0,524 | 0,849 |
| АВВ | 40 000 | 29 000 | 1,09 | 0,5797 | 0,6319 |
| АВС | 48 000 | 35 200 | 1,56 | 0,5769 | 0,9 |
| ВВВ | 45 600 | 24 000 | ? | 0,66 | |
| Средняя арифметическая величина Х по предприятиям-аналогам, Хс | 0,7445 | ||||
| Величина β-коэффициента бета для анализируемого предприятия | β = 0,7445 : 0,66 = 1,12803 |
Решение:
В данном примере исходные данные – основные параметры, характеризующие качество источников финансирования, предприятий-аналогов. Одним из основных показателей качества структуры источников финансирования является доля собственного капитала в общих источниках:
D = СОБС : (СОБС + ЗС),
где
ЗС – заемные средства;
СОБС – собственные средства.
Для оценки уровня риска анализируемого предприятия воспользуемся отношением β-коэффициента и коэффициентом автономии (Кав):
Х = β : (1 : Кав) = β
* Кав.
При среднем фиксированном значении Х, чем больше будет значение Кав, тем меньше будет величина β-коэффициента, тем меньше чувствительность показателей доходности ценных бумаг конкретной компании к изменению рыночного риска.
Исходя из этого рассчитаем значение β-коэффициента, используя следующий алгоритм:
- Рассчитаем значения коэффициента автономии для каждого предприятия аналога и анализируемого предприятия, расчеты этого показателя представлены в столбце 5 табл. 16.30.
-
Определим произведение коэффициента автономии (Кав) и β-коэффициента для компаний аналогов:
Х = Кавк * β.
Расчеты представлены в столбце 6 табл. 16.30, по полученным данным рассчитаем среднюю арифметическую величину Хс.
- Определим β-коэффициент для анализируемого предприятия путем умножения средней арифметической величины Хс на коэффициент автономии анализируемого предприятия:
βан = Хс : Каван.
По расчетным данным табл. 16.30 следует, что чувствительность анализируемого предприятия к макроэкономическим факторам риска составляет 1,128, что больше среднерыночного значения β.
Рассчитаем значение ставки дисконта для инвестора, учитывая, что номинальная ставка дохода для инвестора должна составить 8%, а премия за рыночный риск – 5%.
D = Rf + β
* (Rm – Rf) = 8 + 1,128 * 5 = 13,64%.
Таким образом, уровень доходности от вложения средств в акции данного предприятия должен быть более 13,64%, в противном случае инвестор потеряет часть своих вложений.
Модель САРМ для оценки капитальных активов
В соответствии с моделью САРМ для оценки капитальных активов используется ставка дисконтирования вида:
D = Rck = Rf + β * (Rm – Rf) + S1 + S2 + C,
где
Rf – безрисковая ставка доходности;
β – коэффициент, являющийся мерой систематического риска, связанного с макроэкономическими и политическими процессами, происходящими в стране;
Rm – общая доходность рынка в целом (среднерыночного портфеля ценных бумаг);
Rf – премия за риск;
S1 – премия для малых предприятий;
S2 – премия за риск, характерный для отдельной компании;
C – страновый риск, риск хозяйствования в условиях развивающейся экономики.
Данный метод расчета ставки дисконтирования могут использовать только те организации, которые являются открытыми акционерными обществами, акциями которых торгуют на фондовых рынках, есть статистические данные для расчета β-коэффициента, а также существует аналог-предприятие.
Соответственно, нельзя использовать предприятиям, у которых нет достаточной статистики для расчета своего β-коэффициента, а также не имеющие возможности найти предприятие-аналог, чей β-коэффициент они могли бы использовать в собственных расчетах. Для определения ставки дисконтирования таким компаниям следует использовать иные методы расчета.
Средневзвешенная стоимость капитала WAСС