Как найти доинну отрезка

Как найти доинну отрезка

Длина отрезка. Расстояние между точками: онлайн-калькулятор

Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:

  1. Задать размерность (плоскость или пространство).
  2. Ввести в поля координаты точек.
  3. Нажать «рассчитать».

Расстояние между точками онлайн

Для нахождения длины отрезка по координатам существует формула. Для отрезка AB в трехмерном пространстве она имеет вид:

d=xb-xa2+yb-ya2+zb-za2

Даже если вы забыли данную формулу, расстояние между точками всегда можно найти по координатам онлайн. Калькулятор не только предоставляет правильный ответ, но и подробно расписывает решение.

Онлайн-калькулятор нахождения длины отрезка по координатам будет полезен школьникам и студентам в самостоятельной подготовке, а также преподавателям и всем любителям математики.

Источник

Длина отрезка – это то же самое, что и расстояние между двумя точками.

Можно рассмотреть несколько случаев, когда эта длина неизвестна

пример 1

есть на прямой три точки, которые образуют три отрезка

Чтобы найти отрезок побольше, нужно два меньших сложить.

Чтобы найти меньший отрезок, нужно от большого отнять другой меньший

АС=АВ-СВ или СВ=АВ-АС

пример 2

найдем длину отрезка на координатной прямой.

отрезок лежит между точками А(-5) и В(9), тогда его длина 9-(-5)=14

пример 3

найдем длину отрезка на координатной плоскости.

здесь тоже все просто – по координатам находим длину условных катетов прямоугольного треугольника а дальше по формуле Пифагора находим длину.

Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Начальные геометрические сведения
  5. Длина отрезка

Отрезок – это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.

Измерить отрезок – значит найти его длину (расстояние между его концами).

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

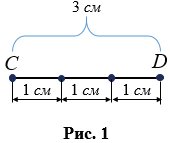
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

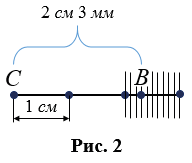
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

         

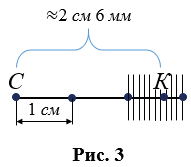
  • Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Длина отрезка – это всегда какое-то положительное число.

Свойства длин отрезков:

  1. Равные отрезки имеют равные длины.
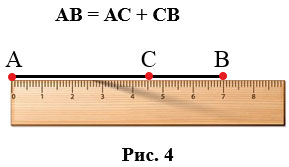
  2. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.

         

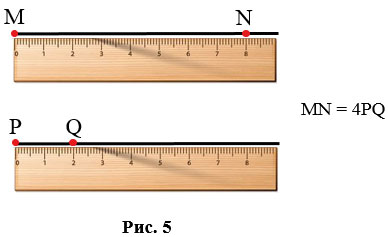
  1. Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.

         

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения


Правило встречается в следующих упражнениях:

7 класс

Задание 32,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 35,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 77,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 79,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 801,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1048,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1279,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник


Загрузить PDF


Загрузить PDF

Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.[1]
 С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.

  1. Изображение с названием Use Distance Formula to Find the Length of a Line Step 1

    1

    Запишите формулу для вычисления длины. Формула: d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}, где d — длина отрезка, (x_{{1}},y_{{1}}) — координаты начальной точки отрезка, (x_{{2}},y_{{2}}) — координаты конечной точки отрезка.[2]

  2. Изображение с названием Use Distance Formula to Find the Length of a Line Step 2

    2

    Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.[3]

  3. Изображение с названием Use Distance Formula to Find the Length of a Line Step 3

    3

    Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты x должны находится внутри первой пары скобок, а две координаты y — внутри второй пары скобок.[4]

    Реклама

  1. Изображение с названием Use Distance Formula to Find the Length of a Line Step 4

    1

    Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.[5]

  2. Изображение с названием Use Distance Formula to Find the Length of a Line Step 5

    2

    Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.[6]

  3. Изображение с названием Use Distance Formula to Find the Length of a Line Step 6

    3

    Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.

  4. Изображение с названием Use Distance Formula to Find the Length of a Line Step 7

    4

    Вычислите длину отрезка d. Для этого извлеките корень из полученной суммы чисел.

    Реклама

Советы

  • Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
  • Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.

Реклама

Об этой статье

Эту страницу просматривали 24 603 раза.

Была ли эта статья полезной?

Источник

Математика

6 класс

Урок № 75

Длина отрезка

Перечень рассматриваемых вопросов:

  • длина отрезка;
  • единицы измерения длины;
  • способы измерения длины отрезка;
  • решение задач на вычисление длины отрезка.

Тезаурус

Отрезок – это часть прямой, ограниченная двумя точками.

Длина отрезка – это расстояние между его концами.

Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.

Длиной отрезка называется положительная величина, определённая для каждого отрезка.

Любой отрезок имеет определённую длину, большую нуля.

Обязательная литература:

  1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

  1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
  2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Что такое отрезок?

Отрезок – это часть прямой, ограниченная двумя точками.

Как отрезки обозначаются на чертежах?

Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.

Любой отрезок имеет определённую длину, большую нуля.

Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.

Длина отрезка – это расстояние между его концами.

Свойства длин отрезков:

– равные отрезки имеют равные длины;

– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.

Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.

Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.

Можно сравнивать длины отрезков, не имея под рукой линейки. Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.

В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.

Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.

Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.

Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.

При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.

Алгоритм измерения длины отрезков:

– выбрать какой-либо отрезок и принять его за единицу длины;

– от одного из концов отрезка отложить последовательно отрезки, равные единичному;

– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;

– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;

– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;

– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.

Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.

На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.

Рассмотрим фигуры, составленные из отрезков.

Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.

Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.

Длина ломаной – это сумма длин всех её звеньев.

Если концы ломаной совпадают, то такая ломаная называется замкнутой.

Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.

Периметр многоугольника равен сумме длин всех его сторон.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.

Впишите верный ответ.

Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.

Решение:

Пусть PB = x, тогда AP = x + 3,6 см.

По условию AB = 10,4 см.

Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

PB + AP = AB.

Составим и решим уравнение:

x + x + 3,6 = 10,4,

2x + 3,6 = 10,4,

2x = 10,4 – 3,6,

2x = 6,8,

x = 3,4.

Значит, длина отрезка PB = 3,4 см.

Ответ: 3,4 см.

Тип 2. Множественный выбор

Выберите верные ответы.

Задача 2

Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.

Варианты ответов: 3,9; 11,1; 4,8; 13,2; 16,5; 2,9.

Первый вариант решения

В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,1 (см).

Второй вариант

BC = AB + AC,

АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).

Значит, длина отрезка АВ может быть равна 11,1 см или 3,9 см. Выбираем эти варианты.

Ответ: 11,1; 3,9.

Источник

Добавить комментарий