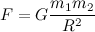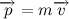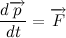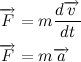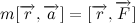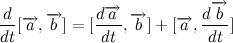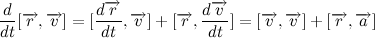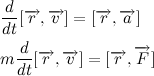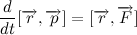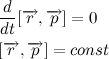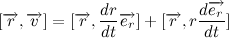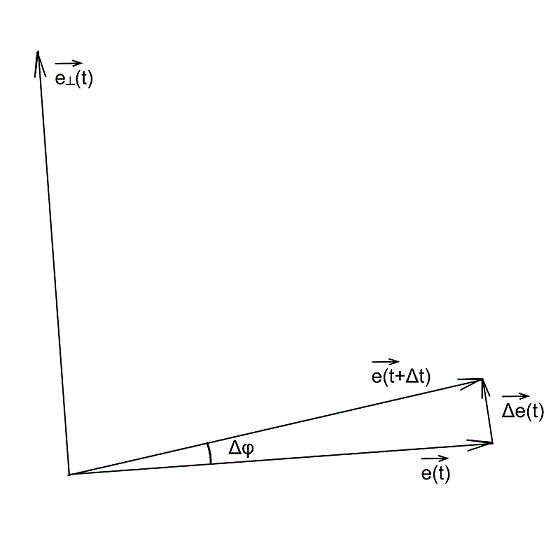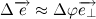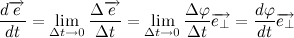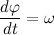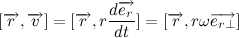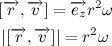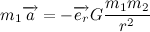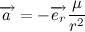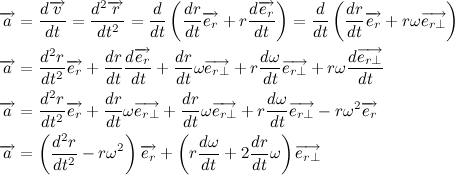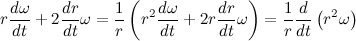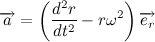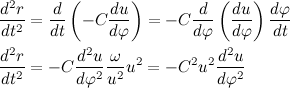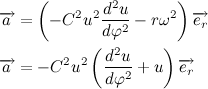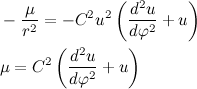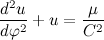Как найти долготу планеты

• Астролог и Я/
• АСТРОШКОЛА/
• Построение гороскопа/
• Построение Гороскопа Вручную
• /Расчет долготы планет

Расчёт долготы планет              

 КРАТКОЕ СОДЕРЖАНИЕ УРОКА

• Определение времени рождения по Гринвичу
• Расчет долготы планет. Теория
• Общий алгоритм расчета
• Расчет долготы планет. Практика

Рассмотрим первый этап построения гороскопа  и сделаем расчет долгот планет гороскопа.

Исходными данными при построении гороскопа являются:

1.) Дата рождения — число, месяц, год

2.) Время рождения

Точность времени рождения очень важна при интерпретации. В случае отсутствия времени рождения, строится космограмма (та же натальная карта, но без системы куспидов домов).

3.) Место рождения — географические широта, долота и часовой пояс.

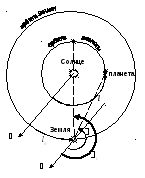
В древности астрологи присутствовали при рождении нового человека, измеряли с помощью сложных приборов координаты звезд и светил. Теперь нам уже не нужно проходить через все эти этапы. У нас есть астрономический помощник – Эфемериды. Это справочник, содержащий всю необходимую нам информацию о движении и нахождении планет в определенный момент времени.

В Эфемеридах Михельсена расчет планет проводится только по Гринвичскому времени. Гринвичское время обозначается Tₒ («Т нулевое»). Гринвичское время является эталонным временем, точкой отсчета. Поэтому все расчеты мы будем проводить на Tₒ.

Чтобы определить Tₒ, нужно из времени Вашего рождения вычесть часовую разницу Гринвичского времени и местного времени, т.е. времени местности, где Вы родились. Для этой процедуры нам нужен Справочник координат городов и временных поправок. Справочник

Рассмотрим пример: Если человек родился в зимнее время в Москве, то разница с Гринвичем будет 3 часа. Следовательно, из времени рождения мы вычитаем 3 часа и смотрим показатели на это, рассчитанное нами время.

На самом деле Москва находится во втором часовом поясе но в 1930 году коммунистическое правительство решило быть «впереди планеты всей» и своим декретом на всей территории страны время было переведено на час вперед. Т.е. если человек родился в 15 часов дня в Москве. Мы из 15 часов вычитаем 3 часа, получаем 12 часов и работаем с данными Эфемерид на 12 часов. Именно это и есть время рождения нашего человека по Гринвичу.

Выяснив время рождения, преступаем к расчету долгот планет. Расчет долгот планет производится методом интерполяции. Интерполяция это нахождение промежуточного значения. Т. е. при условии знания двух определенных значений, мы всегда можем вычислить промежуточное.

В Эфемеридах мы видим значение на 0 часов 00 минут дня рождения и значение на 0 часов 00 минут следующего дня.

Рисунок 1. Для рожденного 3 мая 2014 года, мы возьмем данные на начало 3 мая 2014 г. и на начало 4 мая 2014

 

Мы всегда можем вычислить промежуточное значение, между этими двумя показателями.

Для интерполяции мы будем использовать самый обыкновенный метод — метод пропорции.

Говоря о земном времени, мы употребляем термины: час, минута, секунда. Аналогично и в географических понятиях. Долготы планет выражаются в градусах, минутах и секундах.

Градусы обозначаются: º

Минуты обозначаются: ˊ

Секунды обозначаются: ʺ

Для упрощения расчетов мы постоянно будем переводить градусы в минуты, минуты в секунды и наоборот (при необходимости). Нужно знать, что в градусах 60 минут, а в минуте 60 секунд.

Подготовительную работу мы провели теперь приступим к расчету долгот планет.

Долгота планет обозначается греческой буквой λ (Лямда).

Общий алгоритм расчета:

1. Вычисляем весь путь, пройденный планетой за сутки.

Для этого надо из большей долготы вычесть меньшую. У директивных планет: из долготы на начало следующего за днем рождения вычитаем долготу планеты на начало дня рождения. Данные находим в Эфемеридах. У ретроградных планет: наоборот.

2. Вычисляем какой путь планета прошла от начала суток до момента рождения.

3. Прибавляем результат, полученный в п. 2, к исходной координате, и таким образом, узнаем точную долготу планеты на момент рождения.

В таком расчете есть небольшая неточность. Проблема в том, что пропорция подразумевает равномерное движение планет. Но….. из второго закона Кеплера мы знаем, что планеты движутся неравномерно. Применяя метод пропорции, мы делаем допущение, будто планеты движутся равномерно. Однако, наша ошибка измеряется секундами и имеет отношение только к быстрым планетам. Высшие планеты в течение суток делают крохотные шажки. Солнце и Луна, конечно, требуют более точного расчета. Еще один немаловажный момент: случается, что планета за сутки успевает перейти в следующий знак, в этом случае удобно к позиции планеты прибавить 30 градусов. Т. е. для удобства расчетов 13 градусов Козерога можно принять за 43 градуса Стрельца.

С теорией на сегодня закончим и перейдем к практике. Удобнее завести тетрадь, где указывать результаты расчетов и блокнот, в котором данные расчеты производить.

Для наглядности все данные вносим в табличку.

Таблица состоит из шести столбцов:

1.) Планета

2.) Долгота планеты на начало дня

3.) Долгота на начало следующего дня

4.) Путь, пройденный планетой за сутки

5.) Путь пройденный с начала дня до момента рождения

6.) Долгота планеты на момент рождения

Рисунок 2. Таблица значений

Пример расчета:

 Натив Е. Родилась 7.09.1961 г. То = 20 часов 20 минут

 1.) Путь, пройденный Солнцем

λ Солнца на 8.09 –  λ Солнца на 7.09 = 15º06’06″c — 14º07’50″c = 0º58’16”

 2.) Составляем пропорцию: за 24 часа (сутки) Солнце прошло 0 º 58 ‘ 16 ” дуги, т. е. 58,27 минут (переводим 16 секунд в минуты: 16 секунд делим на 60 получаем 0,27 минут). 

За время от начала суток до момента рождения — 20,3 ч (То =20 часов 20 минут=20,3 ч) — Солнце прошло х минут дуги:

    24 ч — 58,27 ‘
20,3 ч — х ‘
          х = 49,3 ‘

Следовательно, от начала суток до момента рождения Солнце прошло 49,3 минут (49’18”) дуги.

3.) Вычисляем точную долготу Солнца на момент рождения:

λ Солнца на 7.09 = 14º07 ’50″c + 49’18 ” = 14º57’08”.

Аналогично вычисляются все долготы планет на момент рождения. В связи с тем, что Луна движется очень быстро, то имеет смысл при расчетах брать промежуток в 12 часов. Эфемериды содержат информацию о нахождении Луны в 12 часов дня по Гринвичу.

ПОДАРКИ БЛИЗНЕЦАМ НА ДЕНЬ РОЖДЕНИЯ

Время на прочтение
7 мин

Количество просмотров 21K

Не так давно очень активно обсуждалась тема Марса. В то время у меня возник вопрос от которого в силу своего наивного любопытства я никак не мог избавится: «Где Марс находится в данный момент, в какой стороне?» и смежный с ним: «Да и вообще, как определить положение остальных планет?». Очевидно, что траектории движения планет относительно земли будут весьма хитрыми. Конечно, можно воспользоваться планетариями, например таким, но как вы уже поняли, это не наш путь.

В данном цикле статей, я постараюсь максимально просто рассказать о сложном. В результате мы напишем простую программу, которая подскажет где искать планеты нашей Солнечной системы для любой заданной точки на поверхности земли в заданный момент времени. Своей целью я ставлю донести читателю суть того, что скрывается за Кеплеровой моделью орбиты, поэтому я не буду использовать никакие общеизвестные факты кроме законов Ньютона и закона всемирного тяготения.

Всех любопытных прошу под кат.

Стоит отметить, что дальнейшее изложение подразумевает, что читатель немного знаком с законами Ньютона, основными сведениями из геометрии, векторной алгебры и дифференциального исчисления.

Так как же движутся планеты?

В реальности, если учитывать взаимное влияние планет, смещение центра тяжести солнечной системы относительно центра тяжести солнца и т.д. движение планет окажется чрезвычайно сложным и не поддающимся строгому аналитическому определению. Стоит отметить что даже задача о движении трех тел не может быть решена аналитически. Поэтому давайте сразу оговорим в рамках каких моделей мы будем работать. Мы будем рассматривать Кеплерову модель орбиты. Существует большое множество других моделей, но все они являются полуаналитическими и в итоге большинство из них сводится к определению параметров Кеплеровой орбиты в интересующий момент времени. Другими словами, Кеплерова орбита является аппроксимацией сложного движения планеты в заданный момент времени. Кеплеровы параметры орбит планет можно посмотреть здесь nssdc.gsfc.nasa.gov/planetary/factsheet, там же указана эпоха (другими словами момент времени) в момент которой данные параметры Кеплеровой орбиты дают точное положение небесного тела. Обычно этим исходным моментом времени является эпоха J2000.0 (полдень 1 января 2000 года). Расчет движения тел на небольшой промежуток времени при помощи Кеплеровой модели является достаточно точным. Точности вполне хватит, чтобы не заметить ошибку визуально или в небольшой телескоп. Конечно, для расчета траектории полета к другой планете нужны более точные модели.

Кеплерова орбита

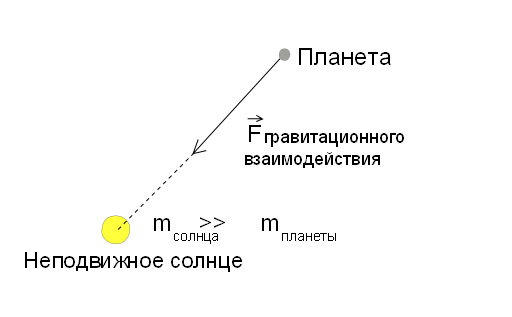
Итак, по порядку. Начнем с основных допущений данной модели. Предполагается, что масса Солнца много больше массы всех планет вместе взятых, откуда можно сделать вывод, что взаимодействие между планетой и планетой пренебрежимо мало по сравнению с взаимодействием между солнцем и планетой. Таким образом, поставленную задачу можно свети к задаче о взаимодействии двух тел (т.е. можно рассмотреть взаимодействии каждой планеты с солнцем отдельно). Более того предполагаем, что масса планеты много меньше массы Солнца, то взаимодействие получается одностороннее, т.е. планета никак не влияет на движение Солнца. Таким образом, мы можем рассматривать планету, как материальную точку, движущуюся в гравитационном поле, центр которого неподвижен. Примерно так:

Гравитационное взаимодействие

Что такое гравитационное взаимодействие? Это универсальное фундаментальное взаимодействие между всеми материальными телами. О гравитации можно говорить много и долго, но нам нужен только ключевой момент. Согласно классической теории тяготения Ньютона, сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

Здесь — G гравитационная постоянная (некий коэффициент пропорциональности). Нам важно отметить лишь то, что сила гравитации направлена от центра тяжести одного тела к центру тяжести другого и обратно пропорциональна квадрату расстояния между ними (закон обратных квадратов).
Отметим, что на нашу

сферическую планету в вакууме

материальную точку не действует никакая другая сила, кроме силы притяжения со стороны Солнца. В нашем случае, поле сил тяготения является центральным полем сил. В центральное поле сил, направление силы действующей на тело в любой точке такого поля, всегда проходит через центр этого поля (в нашем случае через центр тяжести солнца), а величина такой силы зависит только от расстояния до этого центра.

Второй закон Ньютона

Как движется тело под действием силы? На этот вопрос отвечает второй закон Ньютона. Вообще этот закон имеет несколько формулировок, наиболее распространенная из современных:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Данная формулировка точная, но не слишком понятная. Сам Ньютон давал другую формулировку:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Такая формулировка хоть и менее точная (нужно сделать оговорки про системы отчета, но нас это пока не интересует), но куда более понятная. Под количеством движения здесь понимается так называемый импульс тела, равный произведению массы тела на его скорость:

Таким образом, запишем словесную формулировку в символьном виде:

Или же если мы распишем, чему равен импульс тела и вынесем массу как константу (масса не всегда константа, но в нашем случае это так) за знак дифференциала то получим следующую всем известную формулу:

Где вектор 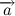— ускорении тела. Не забываем, что ускорение, импульс, скорость и сила величины векторные. Давайте условимся, что если над векторной величиной стоит знак вектора, то понимается именно вектор, в противном случае его модуль.

Второй закон Кеплера

Давайте для простоты, поместим начало координат в центре тяготения, т.е. в центре тяжести Солнца. Таким образом, вектор, проведенный из центра тяжести планеты к началу координат, совпадает по направлению с вектором силы притяжения.
Положение тела в пространстве описывается так называемым радиус-вектором — вектором, проведенным из начала координат к центру тяжести тела. Умножим векторно левую и правую часть выражения на радиус вектор:

Для дальнейших манипуляций, давайте распишем производную векторного произведения:

Тогда производная векторного произведения радиус вектора на скорость:

Напомню, что векторное произведение вектора самого на себя равно нулю, тогда:

Внесем массу под знак дифференциала, и с учетом выражения для импульса тела получим:

Так как вектор силы притяжения всегда направлен к центру тяготения, то векторное произведение радиус вектора на силу притяжения всегда равно нулю, отсюда делаем очень важный вывод:

Мы получили так называемый закон сохранения момента импульса. Изменение момента импульса тела пропорционально приложенному к нему моменту сил. Так как вектор силы притяжения всегда направлен к центру тяготения, то момент силы притяжения относительно центра тяготения всегда равен нулю. Отсюда следует, что момент импульса тела постоянен.
Так как мы договорились, что масса планеты постоянна, то также справедливо и следующее выражение:

Чтобы понять, что такое 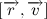, давайте обратимся к рисунку:

На рисунке изображен участок траектории. За время dt тело проходит расстояние vdt. Модуль векторного произведения векторов численно равен площади параллелограмма построенного на этих векторах. Получается, что:

Величина 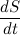есть площадь описываемая радиус вектором за единицу времени и называется она секториальной скоростью. Следовательно, секториальная скорость тела постоянна. Мы только что получили второй закон Кеплера который гласит:

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Да знаю, «получили закон» звучит не хорошо, но что поделаешь, он так называется. Причина в том, что Кеплер его не выводил, а интуитивно подобрал на основе своих наблюдений, т.е. получил его эмпирическим путем, в этом случае это действительно был закон.
Ниже приведена иллюстрация данного закона (рисунок взят из статьи на википедии).

Дифференциальное уравнение орбиты

Давайте все же подробнее рассмотрим векторное произведение радиус вектора на скорость. Радиус вектор можно представить в виде произведения модуля радиус вектора (расстояние от начала координат до точки) на вектор единичной длины, совпадающий по направлению с радиус вектором:


Тогда вектор скорости будет равен:

А векторное произведение радиус вектора на скорость в свою очередь:

Учитывая тот факт, что вектора и совпадают по направлению, а следовательно совпадают по направлению и вектора и , получаем, что . Тогда:

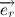
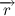
Давайте разберем, что такое производная единичного вектора по времени:

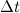
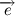
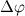
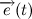
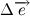
Из рисунка видно, что за время вектор поворачивается на угол . Разность векторов и равна вектору . Для малых углов справедливо следующее соотношение:

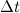
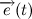
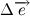
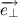
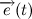
В пределе, когда устремляется к нулю, направления векторов и совпадают, а направление вектора перпендикулярно к ним. Введем единичный вектор , перпендикулярный к и совпадающий с направлением движения его конца, тогда:

Таким образом, переходя к пределу, получим:

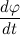
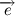
Где это угловая скорость вектора . Обозначим
Вернемся к нашему произведению радиус вектора на скорость, учитывая, что 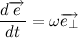получим:

Несложно заметить, что вектора и взаимно перпендикулярны. Введем еще один единичный вектор , который перпендикулярен к векторам и . Таким образом, вектора , и образуют ортонормированный базис. Исходя из определения векторного произведения, получим:

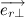
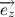
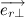
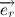
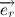
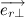
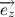
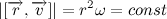
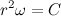
Следовательно, . Введем обозначение, . Так же стоит отметить, что:

Вернемся к второму закону ньютона. Вектор силы действующей на тело распишем сразу как величину гравитационной силы, умноженную на орт :

Где m₁ и m₂ — масса планеты и солнца соответственно.
Давайте на массу планеты сразу сократим, и нигде далее про массу планеты вспоминать не будем, так как она совершенно не влияет на траекторию движения. Будем считать, что мы работаем с телом единичной массы. Введем обозначение, , тогда:

Теперь давайте распишем вектор ускорения:

Рассмотрим содержимое второй скобки:

Но мы уже знаем, что , отсюда следует, что , тогда:

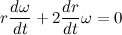
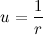
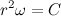
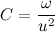
Введем обозначение . Напомню, что раннее мы ввели обозначение , очевидно, что .
Теперь распишем производную от модуля радиус вектора через С:

Теперь распишем вторую производную от модуля радиус вектора через С:

Учитывая полученный результат, перепишем выражение для вектора ускорения:

Тогда второй закон Ньютона примет вид:

Перепишем полученное дифференциальное уравнение в более привычный вид:

Я думаю многие из вас догадались, что представляет из себя полученное дифференциальное уравнение, но я пожалуй закончу на этом первую часть чтобы не перегружать читателя и себя.

Итог

Мы получили дифференциальное уравнение, описывающее траекторию движения материальной точки в гравитационном поле, которое вполне применимо для описания траектории планет и некоторых других небесных тел.

Что нам еще предстоит

В полученном дифференциальном уравнении отсутствует временной параметр, поэтому мы ничего не знаем о характере движения, поэтому необходимо как-то привязаться ко времени. Также далее будут рассмотрены различные системы координат и их преобразования для того чтобы получить координаты планет в системе привязанной к наблюдателю.

P.S.

Любая критика, замечания и дополнения приветствуются.

Законы кеплера и конфигурации планет

Цель
работы:
изучение закономерностей в движении
планет и вычисление их конфигураций.

Пособия:
Астрономический календарь – постоянная
часть или Справочник любителя астрономии;
Астрономический календарь-ежегодник;
Малый звездный атлас А.А. Михайлова;
калькулятор.

Под
действием гравитационного притяжения
к Солнцу планеты обращаются вокруг него
по слабовытянутым эллиптическим орбитам.
Солнце находится в одном из фокусов
эллиптической орбиты планеты. Это
движение подчиняется законам Кеплера.

Величина
большой полуоси
эллиптической орбиты планеты является
также средним расстоянием от планеты
до Солнца. Благодаря незначительным
эксцентриситетами небольшим наклоненияморбит больших планет, можно при решении
многих задач приближенно полагать эти
орбиты круговыми с радиусоми лежащими практически в одной плоскости
– в плоскости эклиптики (плоскости
земной орбиты).

Согласно
третьему закону Кеплера, если
и– соответственно звездные (сидерические)
периоды обращения некоторой планеты и
Земли вокруг Солнца, аи– большие полуоси их орбит, то

.

(7.1)

Здесь
периоды обращения планеты и Земли могут
быть выражены в любых единицах, но
размерности
идолжны быть одинаковы. Подобное
утверждение справедливо и для больших
полуосейи.

Если
за единицу измерения времени принять
1 тропический год (– период обращения Земли вокруг Солнца),
а за единицу измерения расстояния 1
астрономическую единицу (),
то третий закон Кеплера (7.1) можно
переписать в виде

.

(7.2)

Угловая
и линейная скорости планеты при ее
движении на орбите периодически
изменяются в соответствии со вторым
законом Кеплера. Их средние значения
могут быть посчитаны по средней
удаленности
планеты от Солнца.

Средняя
суточная угловая скорость
планеты, определяется выражением

,

(7.3)

где
– сидерический период обращения планеты
вокруг Солнца, выраженный в средних
солнечных сутках.

Очевидно,
для Земли средняя угловая скорость
определяется формулой

(7.4)

и
составляет
.

Поделив
(7.3) на (7.4), получим

.

(7.5)

Если
принять за единицу измерения угловых
скоростей планеты и Земли
,
а периоды обращения измерять в тропических
годах, то формула (7.5) может быть записана
в виде

.

(7.6)

Учтя
третий закон Кеплера (7.2), запишем
зависимость средней угловой скорости
планеты от большой полуоси ее орбиты

.

(7.7)

Средняя
линейная скорость движения планеты на
орбите может быть рассчитана по формуле

,

(7.8)

Аналогичная
величина для Земли

.

(7.9)

Среднее
значение орбитальной скорости Земли
известно и составляет
.
Поделив (7.8) на (7.9) и используя третий
закон Кеплера (7.2), найдем зависимостьот

,

(7.10)

Звездный
(сидерический)
и синодическийпериоды обращения планеты связаны между
собойуравнением
синодического движения

.

(7.11)

Знак
«-» соответствует внутренним
или нижним планетам (Меркурий, Венера),
а «+» – внешним
или верхним (Марс, Юпитер, Сатурн, Уран,
Нептун). В этой формуле
ивыражены в годах. В случае необходимости
найденные значенияивсегда могут быть выражены в сутках.

Взаимное
расположение планет легко устанавливается
по их гелиоцентрическим эклиптическим
сферическим координатам, значения
которых на различные дни года публикуются
в астрономических календарях-ежегодниках,
в таблице под названием «гелиоцентрические
долготы планет».

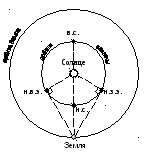
Центром
этой системы координат (рис. 7.1) является
центр Солнца, а основным кругом –
эклиптика, полюса которой
иотстоят от нее на 90º.

Большие
круги, проведенные через полюса эклиптики,
называются кругами
эклиптической широты,
по ним отсчитывается от эклиптики
гелиоцентрическая
эклиптическая широта
,
которая считается положительной в
северном эклиптическом полушарии и
отрицательной в южном эклиптическом
полушарии небесной сферы. Гелиоцентрическая
эклиптическая долгота
отсчитывается
по эклиптике от точки весеннего
равноденствия 
против часовой стрелки до основания
круга широты светила и имеет значения
в пределах от 0º до 360º.

Из-за
малого наклонения орбит больших планет
к плоскости эклиптики, эти орбиты всегда
находятся вблизи эклиптики, и в первом
приближении можно считать их
гелиоцентрическую долготу
,
определяя положение планеты относительно
Солнца лишь одной ее гелиоцентрической
эклиптической долготой.

Рис.
7.1. Эклиптическая система небесных
координат

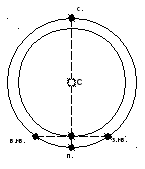
Рассмотрим
орбиты Земли и некоторой внутренней
планеты (рис. 7.2), используя гелиоцентрическую
эклиптическую систему координат.
В ней основным кругом является эклиптика,
а нуль-пунктом – точка весеннего
равноденствия .
Отсчет
эклиптической гелиоцентрической долготы
планеты ведется от направления «Солнце
– точка весеннего равноденствия »
до направления «Солнце – планета»
против часовой стрелки. Для простоты
будем считать плоскости орбит Земли и
планеты совпадающими, а сами орбиты –
круговыми. Тогда положение планеты на
орбите задается ее эклиптической
гелиоцентрической долготой
.

Если
центр эклиптической системы координат
совместить с центром Земли, то это будет
геоцентрическая
эклиптическая система координат.
Тогда угол между направлениями «центр
Земли – точка весеннего равноденствия
»
и «центр Земли – планета» называется
эклиптической
геоцентрической долготой
планеты
.
Гелиоцентрическая эклиптическая долгота
Землии геоцентрическая эклиптическая долгота
Солнца,
как видно из рис. 7.2, связаны соотношением:

.

(7.12)

Будем
называть конфигурацией
планеты
некоторое фиксированное взаимное
расположение планеты, Земли и Солнца.

Рассмотрим
раздельно конфигурации внутренних и
внешних планет.

Рис.
7.2. Гелио- и геоцентрическая системы

эклиптических координат

Различают
четыре конфигурации внутренних планет:
нижнее
соединение
(н.с.), верхнее
соединение
(в.с.), наибольшая
западная элонгация
(н.з.э.) и наибольшая
восточная элонгация
(н.в.э.).

В
нижнем соединении (н.с.) внутренняя
планета находится на прямой, соединяющей
Солнце и Землю, между Солнцем и Землей
(рис. 7.3). Для земного наблюдателя в этот
момент внутренняя планета «соединяется»
с Солнцем, то есть видна на фоне Солнца.
При этом эклиптические геоцентрические
долготы Солнца и внутренней планеты
равны, то есть:
.

Вблизи
нижнего соединения планета перемещается
на небе в попятном движении около Солнца,
над горизонтом находится днем, причем
около Солнца, и наблюдать ее, разглядывая
что-либо на ее поверхности, невозможно.
Очень редко удается увидеть уникальное
астрономическое явление – прохождение
внутренней планеты (Меркурия или Венеры)
по диску Солнца.

Рис.
7.3. Конфигурации внутренних планет

Так
как угловая скорость внутренней планеты
больше угловой скорости Земли, через
некоторое время планета сместится в
положение, где направления «планета-Солнце»
и «планета-Земля» отличаются на
(рис. 7.3). Для земного наблюдателя планета
при этом удалена от солнечного диска
на максимальный угол, или говорят, что
планета в этот момент находится в
наибольшей элонгации (удалении от
Солнца). Различают две наибольших
элонгации внутренней планеты –западную
(н.з.э.) и восточную
(н.в.э.). В наибольшей западной элонгации
()
и планета заходит за горизонт и восходит
раньше, чем Солнце. Это значит, что
наблюдать ее можно утром, перед восходом
Солнца, в восточной стороне неба. Это
называетсяутренней
видимостью
планеты.

После
прохождения наибольшей западной
элонгации диск планеты начинает
приближаться на небесной сфере к диску
Солнца до тех пор, пока планета не
исчезнет за диском Солнца. Эта конфигурация,
когда Земля, Солнце и планета лежат на
одной прямой, причем планета находится
за Солнцем, называется верхним
соединением
(в.с.) планеты. Проводить в этот момент
наблюдения внутренней планеты нельзя.

После
верхнего соединения угловое расстояние
между планетой и Солнцем начинает расти,
достигая максимального значения в
наибольшей восточной элонгации (н.в.э.).
При этом гелиоцентрическая эклиптическая
долгота планеты больше, чем у Солнца
(а геоцентрическая – наоборот, меньше,
то есть).
Планета в этой конфигурации восходит
и заходит позднее Солнца, что дает
возможность наблюдать ее вечером после
захода Солнца (вечерняя
видимость).

Из-за
эллиптичности орбит планет и Земли угол
между направлениями на Солнце и на
планету в наибольшей элонгации не
постоянен, а изменяется в некоторых
пределах, для Меркурия – от
до,
для Венеры – отдо.

Наибольшие
элонгации – самые удобные моменты для
наблюдений внутренних планет. Но так
как даже в этих конфигурациях Меркурий
и Венера не отходят на небесной сфере
далеко от Солнца, наблюдать их в течение
всей ночи нельзя. Продолжительность
вечерней (и утренней) видимости у Венеры
не превышает 4 часов, а у Меркурия – не
более 1.5 часа. Можно сказать, что Меркурий
всегда «купается» в солнечных лучах –
его приходится наблюдать или непосредственно
перед восходом Солнца, или сразу после
захода, на светлом небе. Видимый блеск
(звездная величина) Меркурия меняется
со временем в пределах от
до.
Видимая звездная величина Венеры
варьируется отдо.
Венера – самый яркий объект на небе
после Солнца и Луны.

У
внешних планет также различают четыре
конфигурации (рис. 7.4): соединение
(с.), противостояние
(п.), восточная
и западная
квадратуры
(з.кв. и в.кв.).

Рис.
7.4. Конфигурации внешних планет

В
конфигурации «соединение» внешняя
планета расположена на прямой, соединяющей
Солнце и Землю, за Солнцем. В этот момент
наблюдать ее нельзя.

Так
как угловая скорость внешней планеты
меньше, чем у Земли, дальнейшее
относительное движение планеты на
небесной сфере будет попятным. При этом
она постепенно будет смещаться к западу
от Солнца. Когда угловое удаление внешней
планеты от Солнца достигнет
,
она попадет в конфигурацию «западная
квадратура». При этом планета будет
видна в восточной стороне неба всю
вторую половину ночи до восхода.

В
конфигурации «противостояние», называемой
иногда также «оппозиция», планета
отстоит на небе от Солнца на
,
тогда

,	(7.13)
.	(7.14)

После
противостояния внешняя планета постепенно
приближается к Солнцу, находясь на небе
восточнее, то есть, левее нашего дневного
светила. В этот период планету можно
наблюдать вечером после захода Солнца.
Когда угловое удаление Солнца достигнет
,
наступит конфигурация «восточная
квадратура», при этом геоцентрическая
эклиптическая долгота планеты

.

(7.15)

Планету,
находящуюся в восточной квадратуре,
можно наблюдать с вечера до полуночи.

Наиболее
благоприятны условия для наблюдений
внешних планет в эпоху их противостояния.
В это время планета доступна наблюдениям
в течение всей ночи. При этом она
максимально сближена с Землей и имеет
наибольший угловой диаметр и максимальный
блеск. Для наблюдателей немаловажно,
что все верхние планеты достигают
наибольшей высоты над горизонтом в
зимние противостояния, когда они движутся
по небу в тех же созвездиях, где Солнце
бывает летом. Летние же противостояния
на северных широтах происходят низко
над горизонтом, что может весьма
затруднить наблюдения.

При
расчете даты той или иной конфигурации
планеты ее расположение относительно
Солнца изображается на чертеже, плоскость
которого принимается за плоскость
эклиптики. Направление на точку весеннего
равноденствия 
выбирается
произвольно. Если задан день года, в
который гелиоцентрическая эклиптическая
долгота Земли
имеет определенное значение, то сначала
следует отметить на чертеже расположение
Земли.

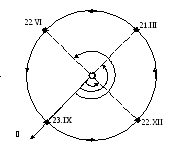
Приближенное
значение гелиоцентрической эклиптической
долготы Земли очень легко найти по дате
наблюдения. Легко видеть (рис. 7.5), что,
например, 21 марта, смотря с Земли в
сторону Солнца, мы смотрим в точку
весеннего равноденствия ,
то
есть, направление «Солнце – точка
весеннего равноденствия» отличается
от направления «Солнце – Земля» на
,
а это значит, что гелиоцентрическая
эклиптическая долгота Земли.
Смотря на Солнце в день осеннего
равноденствия (23 сентября), мы видим его
в направлении на точку осеннего
равноденствия (на чертеже она диаметрально
противоположна точке).
При этом эклиптическая долгота Земли
.
Из рис. 7.5 видно, что в день зимнего
солнцестояния (22 декабря) эклиптическая
долгота Земли,
а в день летнего солнцестояния (22 июня)
–.

Рис.
7.5. Эклиптические гелиоцентрические
долготы Земли
в разные дни года

Для
расчета долготы Земли
в произвольный день года достаточно
вспомнить, что полный оборот ввокруг Солнца Земля совершает за 365
дней. Это значит, что за сутки Земля
смещается по своей орбите примерно на.
Например, 1 апреля эклиптическая
гелиоцентрическая долгота Земли будет,
так как эта дата наступает через 10 дней
после дня весеннего равноденствия,
когда.

Гелиоцентрическая
эклиптическая долгота Земли
в определенные дни года может быть также
найдена по геоцентрической эклиптической
долготе Солнцав эти же дни, так как если построить
подобную систему эклиптических координат
с началом в центре Земли, то всегда,
поскольку Солнце и Земля всегда находятся
на противоположных концах одного
радиуса-вектора. Но геоцентрическая
долготапланеты не связана подобной зависимостью
со своей гелиоцентрической долготой.

Затем
надо изобразить на чертеже орбиту
планеты. Как уже отмечалось, ее можно
считать круговой и изображать с помощью
циркуля. Крайне важно соблюсти пропорции
между радиусами орбит Земли и планеты,
в противном случае измерения углов
транспортиром окажутся неверными.
Напомним, что радиус орбиты Меркурия
примерно
,
Венеры –,
Марса –,
Юпитера –

Теперь
можно наносить на этот чертеж расположение
планеты либо по ее известной
гелиоцентрической эклиптической долготе
,
либо по заданной конфигурации.

Построив
на чертеже положения планет относительно
Солнца, можно измерить транспортиром
их геоцентрические долготы
и по разности

,

(7.16)

определить
условия их видимости с Земли, полагая,
что в среднем планета становится видимой
при удалении от Солнца на угол около
15º.

В
действительности же условия видимости
планет зависят не только от их удаления
от Солнца, но также и от их склонения
и от географической широтыместа наблюдения, которая влияет на
продолжительность сумерек и на высоту
планет над горизонтом.

Так
как положение Солнца на эклиптике хорошо
известно для каждого дня года, то по
звездной карте и по значениям
легко указать созвездие, в котором
находится планета в тот же день года.
Решение этой задачи облегчается тем,
что на нижнем обрезе карт Малого звездного
атласа А.А. Михайлова красными числами
проставлены даты, в которые отмеченные
ими круги склонения кульминируют в
среднюю полночь. Эти же даты показывают
приблизительное положение Земли на
своей орбите по наблюдениям с Солнца.
Поэтому, определив по карте экваториальные
координатыиточки эклиптики, кульминирующей в
среднюю полночь заданной даты, легко
найти для этой же даты экваториальные
координаты Солнца

(7.17)

и
по ним показать его положение на
эклиптике.

По
гелиоцентрической долготе планет легко
вычислить дни (даты) наступления их
различных конфигураций. Для этого
достаточно перейти к системе отсчета,
связанной с планетой. Это предполагает,
что в конечном итоге мы планету будем
считать неподвижной, а Землю – движущейся
по своей орбите, но с относительной
угловой скоростью.

Получим
необходимые формулы для изучения
движения верхней планеты. Пусть в
некоторый день года
гелиоцентрическая долгота верхней
планеты есть,
а гелиоцентрическая долгота Земли –.
Верхняя планета движется медленнее
Земли (),
которая догоняет планету, и в какой-то
день годапри гелиоцентрической долготе планетыи Землинаступит искомая конфигурация планеты.
Тогда

,	(7.18)
,	(7.19)

откуда,
обозначив
,и,
получим

(7.20)

и
найдем

.

(7.21)

Легко
видно, что
представляет собой угловой путь Земли
по орбите, проходимый Землей с относительной
угловой скоростьюза промежуток времени.
Поэтому для вычисленияможно полагать планету неподвижной и,
взяв разностьмежду разностями гелиоцентрической
долготы Земли и планеты в моменты времении(или найдяпо чертежу), сразу определить.
Для вычисления же гелиоцентрической
долготы планетыи Землина датуиспользуются формулы (7.18) и (7.19).

Очевидно,
те же формулы (7.18) – (7.21) служат для
вычисления дней наступления конфигураций
нижних планет с той лишь разницей, что
из-за большой скорости движения нижней
планеты по сравнению со скоростью
движения Земли в формулы следует
подставлять
и дугу,
которую проходит нижняя планета от
одной конфигурации до другой при условии
неподвижной Земли.

Все
рассмотренные выше задачи следует
решать приближенно, округляя значения
до 0,01 астрономической единицы,и– до 0,01 года и– до целых суток.

На Главную

Калькуляторы (Солнце, Луна, планеты):

Солнце восход, заход:

---

• вариант 1 вариант 2 вариант 3
• вариант 4 вариант 5 вариант 6

---

Солнце (восход,кульминация,заход):
• вариант 1

---

Луна восход, заход:

---

• вариант 1 вариант 2 вариант 3

---

Солнце и Луна восход, заход:

---

• вариант 1 вариант 2 вариант 3

---

Солнце,Луна,планеты (восход,кульминация,заход)

---

• вариант 1 вариант 2 вариант 3

---

• Солнце и планеты восход, заход

---

• Солнце, планеты (прямое восх.,склонение)
• Солнце калькулятор
• Солнца, Луна текущее положение

---

Фаза Луны:

---

• Фаза Луны-1
• Фазы Луны-2
• Фаза Луны(в зодиаке)
• Фаза Луны (возраст Луны)
• Фазы Луны на любой месяц
• Фаза Луны на любую дату,(вариант 1)
• Фаза Луны на любую дату,(вариант 2)
• Фаза Луны на любую дату,(вариант 3)
• Календарь фаза Луны на месяц
• Календарь лунных фаз
• Текущая фаза Луны,(вариант 1)
• Текущая фаза Луны,(вариант 2)
• Расчёт лунных дней
• Расчет фаз Луны и лунного дня по Гринвичу
• Расчёт новолуния и полнолуния
• Луна в Перигее и Апогее. Новая и Полная Луна

---

Позиция планет на карте:

---

• вариант 1 вариант 2
• вариант 3 вариант 4

---

Текущее положение планет:

---

• вариант 1 вариант 2
• на сегодня

---

• График положения спутников Юпитера (1950-2050)

---

Текущее положение спутников:

---

Юпитера:
• вариант 1 вариант 2
• вариант 3 вариант 4
• вариант 5 вариант 6

---

Сатурна:
• вариант 1 вариант 2

---

Урана:
• вариант 1

---

Нептуна:
• вариант 1

---

Вид звёздного неба:
• текущий с планетами
• с планетами на любое время

---

В реальном времени:
• Планеты
• Астероиды
• Вояджер 1-2

---

Затмения Солнца:

---

• Калькулятор Солнечного затмения (1970-2039 г.)
• Карты покрытия солнечных затмений (1900-2100)
• Путь Солнечных затмений: (1901 — 2100),(вариант 1)
• Путь Солнечных затмений: (1961 — 2100),(вариант 2)
• Солнечные затмения
• Солнечные затмения (1-3000 годы)

---

Затмения Луны:

---

• Лунные затмения (1-3000 годы)
• Лунные затмения
• Калькулятор Лунных затмений, фаз Луны

---

• Симулятор Солнечной системы
• Модель Солнечной системы

---

Астрономический календарь явлений:

---

• вариант 1 вариант 2

---

Астрономический календарь событий (1800-2100 г.):

---

• вариант 1 вариант 2

---

Альманах:

---

• вариант 2 вариант 3 вариант 7
• Текущее положение планет Солнечной системы
• Планетные конфигурации на любой промежуток времени

---

Эфемериды Солнца, Луны и планет
• вариант 1 вариант 2 вариант 3

---

• Марс – формы петли в противостоянии (1995-2035)

Элонгация,видимость,эфемериды:

---

• Планеты
• Кометы

---

• Солнце и Луна восход, заход(на месяц)
• Астрономические координаты планет
• Видимость планет над горизонтом
• Расчет планет в знаках зодиаках
• Эфемериды Луны для вашего города
• Эфемериды планет
• Эфемериды астероидов
• Элонгация планет на текущий год
• Элонгация планет 1900-2100 гг.(график)
• Планеты в сумерках на текущий год
• Солнце в Зодиакальных созвездиях
• Знаки Зодиака
• Небо месяца
• Транзит Меркурия(2003-2098)
• Видимость планет (график)
• Меркурий элонгация
• Венера элонгация
• Нижнее соединение Венеры
• Сезоны года
• Продолжительность дней
• Прохождение Венеры по диску Солнца
  (с -1998 по 3956 годы)

---

Расчет Эфемерид:

---

• Планет
• Астероидов
• Комет

---

Эфемериды на текущий месяц:

---

• Солнце
• Луны
• Меркурия
• Венеры
• Марса
• Юпитера
• Сатурна

---

Эфемериды на +365 дней:

---

• Солнце
• Луна
• Меркурий
• Венера
• Марс
• Юпитер
• Сатурн
• Уран
• Нептун

---

Соединение планет (-600 – 2400 г.):

---

• Меркурий ☌ ☉
• Меркурий ☌ ♀
• Венера ☌ ☉
• Венера ☌ ♂
• Венера ☌ ♃
• Венера ☌ ♄
• Венера ☌ ♅
• Венера ☌ ♆
• Марс ☌ ☉
• Марс ☌ ♃
• Марс ☌ ♄
• Марс ☌ ♅
• Марс ☌ ♆
• Марс ☌ ♇
• Юпитер ☌ ♄, ♅, ♆, ♇
• Сатурн ☌ ♅, ♆, ♇
• Уран ☌ ♆, ♇
• Нептун ☌ ♇

---

Ретроградное движение планет (-600 – 2400 г.):

---

• Меркурий
• Венера
• Марс
• Юпитер
• Сатурн
• Уран
• Нептун
• Плутон

---

Вход планет в знак (1800-2155 г.):

---

• Солнце
• Меркурий
• Венера
• Марс
• Уран

---

Вход планет в знак (-600 – 2400 г.):

---

• Юпитер
• Сатурн
• ♆, ♇

---

Конфигурация планет (2000-2050 г.):

---

• Марс
• Юпитер
• Сатурн

---

Соединение планет:

---

• 2000-2050 г.

---

Видимый путь:

---

• планет на небе
• движения планет в 2008-2029 годах

---

Тропические Эфемериды:

---

• 2010-2024 годов

---