Как найти долю людей

Как найти долю людей

Что такое доля населения?

  • Редакция Кодкампа

17 авг. 2022 г.
читать 2 мин

В статистике доля населения относится к доле людей в популяции с определенной характеристикой.

Например, предположим, что 43,8% жителей определенного города поддерживают новый закон. Значение 0,438 представляет долю населения.

Формула доли населения

Доля населения всегда находится в диапазоне от 0 до 1 (или от 0% до 100% в процентном выражении) и рассчитывается следующим образом:

р = Х/Н

куда:

  • p: Доля населения
  • X: количество особей в популяции с определенной характеристикой.
  • N: Общее количество особей в популяции.

Как оценить долю населения

Поскольку обычно сбор данных для каждого человека в популяции занимает слишком много времени и средств, вместо этого мы часто собираем данные для выборки.

Например, предположим, что мы хотим узнать, какая часть жителей определенного города поддерживает новый закон. Если население состоит из 50 000 жителей, мы можем взять простую случайную выборку из 1000 жителей:

Затем мы рассчитываем долю выборки следующим образом:

р̂ = х / п

куда:

  • p̂: доля выборки
  • x: количество лиц в выборке с определенной характеристикой.
  • n: общее количество лиц в выборке.

Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 367 из 1000 жителей выборки поддержали новый закон, то доля выборки будет рассчитана как 367/1000 = 0,367 .

Таким образом, наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,367 .

Доверительный интервал для доли населения

Хотя пропорция выборки дает нам оценку истинной доли населения, нет никакой гарантии, что пропорция выборки будет точно соответствовать пропорции населения.

По этой причине мы обычно строим доверительный интервал — диапазон значений, которые, вероятно, содержат истинную долю населения с высокой степенью достоверности.

Формула для расчета доверительного интервала для доли населения :

Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n

куда:

  • p̂: доля выборки
  • z: выбранное значение z
  • n: размер выборки

Z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:

| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |

Обратите внимание, что более высокие уровни достоверности соответствуют большим значениям z, что приводит к более широким доверительным интервалам. Это означает, что, например, 95-процентный доверительный интервал будет шире, чем 90-процентный доверительный интервал для того же набора данных.

Пример: доверительный интервал для доли населения

Предположим, мы хотим оценить долю жителей города, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:

  • Размер выборки n = 100
  • Доля в пользу закона p̂ = 0,56

Вот как найти различные доверительные интервалы для доли населения:

90% доверительный интервал: 0,56 +/- 1,645 * (√ 0,56 (1-0,56) / 100 ) = [0,478, 0,642]

95% доверительный интервал: 0,56 +/- 1,96 * (√ 0,56 (1-0,56) / 100 ) = [0,463, 0,657]

99% доверительный интервал: 0,56 +/- 2,58 * (√ 0,56 (1-0,56) / 100 ) = [0,432, 0,688]

Примечание. Вы также можете найти эти доверительные интервалы с помощью калькулятора доверительного интервала для пропорции .

Источник

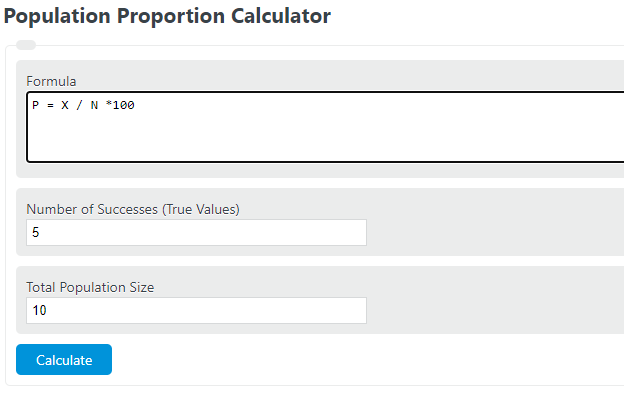
Unit Converter

Enter the number of total successes and the total size of the population into the calculator to determine the population proportion. This calculator can also determine the population size or number of successes given the other variables.

  • Population Density Calculator
  • Population Growth Calculator
  • Confidence Interval Calculator (1 or 2 means)
  • Maximum Usual Value Calculator

The following is the population proportion:

  • Where P is the population proportion (%)
  • X is the number of successes
  • N is the size of the population

To calculate a population proportion, divide the number of successes by the population size, then multiply by 100 to express the result as a percentage.

Population Proportion Definition

A population proportion is defined as a parameter describing the ratio or percentage of a population that has a certain association. For example, the percentage of people that are male, have brown hair, etc.

Can a population proportion be negative?

A population proportion cannot be negative because the values that make up the ratio, which is a number of successes and population size, cannot be less than 0.

Is population proportion the same as standard deviation?

A population proportion is not the same as a standard deviation. A population proportion describes the percentage of a total population that has a value, while a standard deviation describes the variance from the mean of a set of data.

What does a population proportion represent?

A population proportion represents the ratio of the number of people or things in a greater population or set of data that have a certain characteristic. This ratio can often be presented as a percentage for simplicity.

When to use population mean vs population proportion?

You should use population mean when analyzing a characteristic of a population that each person or data point has a varying amount of that characteristic. You should use a population proportion when that characteristic is being measured in a yes or no situation, such as if a person has or doesn’t have brown hair.

How to calculate a population proportion?

  1. First, determine the characteristic or parameter to be analyzed. For example, this could be the number of people that own a car in a certain population.
  2. Next, measure the total number of people that have that characteristic. For this example, we will say that 500 people have a car.
  3. Next, determine the total population. We will say that there are 1,000 people in the population.
  4. Finally, calculate the population proportion using the formula: P = 500/1000 = .50 = 50%.

population proportion calculator
population proportion formula

Источник

Доля населения Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Количество успехов: 30 –> Конверсия не требуется
Численность населения: 50 –> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0.6 –> Конверсия не требуется




4 Пропорции Калькуляторы

Доля населения формула

Доля населения = Количество успехов/Численность населения

PPopulation = NSuccess/NPopulation

Что такое статистическая пропорция и ее значение?

В статистике некоторые конкретные числовые отношения, которые связывают некоторые важные переменные или параметры, связанные с данными или распределением, называются статистическими пропорциями. Сравнение нескольких данных является основным преимуществом этих пропорций. В статистическом анализе данных различные пропорции имеют широкое применение. Например, во время сравнения двух разных данных, сравнения показателей компании с показателями прошлого года, сравнения качества одного набора продуктов со следующим набором продуктов и т. д., если мы сравниваем фиксированную долю каждой группы данных. , мы можем сделать много полезных выводов.

Источник

В статистике , население доля , как правило , обозначается или греческая буква , это параметр , который описывает процентное значение , связанное с населением . Например, перепись США 2010 года показала, что 83,7% американского населения были идентифицированы как не латиноамериканцы или латиноамериканцы; значение 0,837 – это доля населения. В целом, доля населения и другие параметры популяции неизвестны. Перепись может проводиться с целью определения фактического значения параметра населения, но часто перепись не практично из – за его стоимость и затраты времени.
п Пи

Доля населения обычно оценивается с помощью объективной статистики выборки, полученной в результате наблюдательного исследования или эксперимента . Например, Национальная конференция по технологической грамотности провела национальный опрос 2000 взрослых, чтобы определить процент экономически неграмотных взрослых. Исследование показало, что 72% из 2000 опрошенных взрослых не понимали, что такое валовой внутренний продукт . Значение 72% – это примерная пропорция. Доля выборки обычно обозначается, а в некоторых учебниках – .
{ hat {p}}п

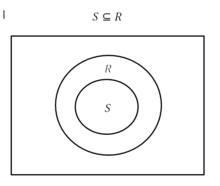
Математическое определение

Иллюстрация набора и его подмножества на диаграмме Венна . Долю можно рассчитать, измерив, сколько из них находится в .рSSр

Доля математически определяется как отношение значений в подгруппе до значений в наборе .
Sр

Таким образом, долю населения можно определить следующим образом:

{ displaystyle P = { frac {X} {N}}} (где – количество успехов в популяции, а – размер популяции)
ИксN

Это математическое определение можно обобщить, чтобы дать определение пропорции образца:

{ displaystyle { hat {p}} = { frac {x} {n}}} (где – количество успехов в выборке, а – размер выборки, полученной из совокупности).
Иксп

Предварительный расчет

Одним из основных направлений исследований в выводной статистике является определение «истинного» значения параметра. Как правило, фактическое значение параметра никогда не будет найдено, если только не будет проведена перепись изучаемого населения. Однако есть статистические методы, которые можно использовать для получения разумной оценки параметра. Эти методы включают доверительные интервалы и проверку гипотез .

Оценка стоимости доли населения может иметь большое значение в областях сельского хозяйства , бизнеса , экономики , образования , инженерии , экологических исследований , медицины , права , политологии , психологии и социологии .

Долю населения можно оценить с помощью доверительного интервала, известного как доля одной выборки в Z-интервале , формула которого приведена ниже:

{ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}} (где – доля выборки, – размер выборки, – верхнее критическое значение стандартного нормального распределения для уровня достоверности )
{ hat {p}}пz ^ {*}{ displaystyle { frac {1-C} {2}}}{ displaystyle C}

Доказательство

Для того чтобы получить формулу для одного образца пропорции в Z-интервала , распределение выборки образцов потребностей пропорции должны быть приняты во внимание. Среднее значение выборочного распределения пропорций выборки обычно обозначается как, а его стандартное отклонение обозначается как . Поскольку значение неизвестно, будет использоваться несмещенная статистика . Среднее и стандартное отклонение переписываются как и соответственно. Ссылаясь на центральную предельную теорему , распределение выборки пропорций выборки является приблизительно нормальным – при условии, что выборка достаточно велика и не перекручена.
{ displaystyle mu _ { hat {p}} = P}{ displaystyle sigma _ { hat {p}} = { sqrt { frac {P (1-P)} {n}}}}п{ hat {p}}п{ displaystyle mu _ { hat {p}} = { hat {p}}}{ displaystyle sigma _ { hat {p}} = { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}

Предположим, вычисляется следующая вероятность:, где и – стандартные критические значения.
{ displaystyle P (-z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}}} (1 - { hat {p}}) )} {n}}}} <z ^ {*}) = C}{ displaystyle 0 <C <1}{ displaystyle pm z ^ {*}}

Распределение выборки пропорций выборки является приблизительно нормальным, когда оно удовлетворяет требованиям Центральной предельной теоремы.

Неравенство может быть алгебраически переписано следующим образом :
{ displaystyle -z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}} <z ^ {*}}

{ displaystyle -z ^ {*} <{ frac {{ hat {p}} - P} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}} <z ^ {*} Rightarrow -z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}} } <{ hat {p}} - P <z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow - { hat {p}} - z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} <- P <- { hat {p}} + z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow { hat { p}} - z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} <P <{ hat {p}} + z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}Из алгебраической проделанной работы выше, очевидно , от уровня уверенности , что может упасть между значениями .
Cп{ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}}}

Условия для вывода

Как правило, формула, используемая для оценки доли населения, требует замены известных числовых значений. Однако эти числовые значения не могут быть подставлены в формулу «вслепую», поскольку статистический вывод требует, чтобы оценка неизвестного параметра была обоснованной. Чтобы оценка параметра была обоснованной, необходимо проверить три условия:

  1. Индивидуальное наблюдение данных должно быть получено из простой случайной выборки из интересующей совокупности.
  2. Отдельные наблюдения данных должны отображать нормальность . Это можно проверить математически с помощью следующего определения:
  3. Отдельные наблюдения данных должны быть независимыми друг от друга. Это можно проверить математически с помощью следующего определения:

Условия для SRS, нормальности и независимости иногда называют условиями для набора инструментов вывода в большинстве статистических учебников.

Пример

Предположим, президентские выборы проходят в условиях демократии. Случайная выборка из 400 имеющих право голоса избирателей из числа избирателей демократического государства показывает, что 272 избирателя поддерживают кандидата B. Политолог хочет определить, какой процент избирателей поддерживает кандидата B.

Чтобы ответить на вопрос политолога, можно построить одновыборочную пропорцию в Z-интервале с уровнем достоверности 95%, чтобы определить долю населения, имеющую право голоса в этой демократии, которая поддерживает кандидата B.

Решение

Из случайной выборки известно, что размер выборки . Перед построением доверительного интервала будут проверены условия вывода.
{ displaystyle { hat {p}} = { frac {272} {400}} = 0,68}{ displaystyle n = 400}

{ Displaystyle (400) (0,68) geq 10 Rightarrow 272 geq 10} а также { Displaystyle (400) (1-0,68) geq 10 Rightarrow 128 geq 10}
Условие нормальности выполнено.
{ Displaystyle N geq 10 (400) Rightarrow N geq 4000}
Численность населения для избирателей этой демократии можно считать , по крайней мере 4000. Следовательно, условие независимости было выполнено.N

После проверки условий вывода можно построить доверительный интервал.

Пусть и{ displaystyle { hat {p}} = 0,68, n = 400,}{ displaystyle C = 0,95}

Чтобы найти , используется выражение .
z ^ {*} { displaystyle { frac {1-C} {2}}}

{ displaystyle { frac {1-C} {2}} = { frac {1-0,95} {2}} = { frac {0,05} {2}} = 0,0250}

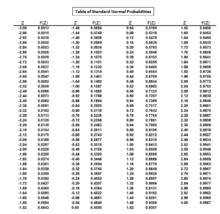
Стандартная нормальная кривая дает площадь верхнего хвоста 0,0250 и площадь 0,9750 для .z ^ {*}{ Displaystyle Z Leq Z ^ {*}}

Таблица со стандартными нормальными вероятностями для .{ Displaystyle Z leq z}

Изучая стандартную нормальную колоколообразную кривую, можно определить значение, определяя, какая стандартная оценка дает стандартной нормальной кривой площадь верхнего хвоста 0,0250 или площадь 1–0,0250 = 0,9750. Значение можно также найти с помощью таблицы стандартных нормальных вероятностей.
z ^ {*}z ^ {*}

Из таблицы стандартных нормальных вероятностей значение, которое дает площадь 0,9750, составляет 1,96. Следовательно, значение равно 1,96.
Zz ^ {*}

Значения , , теперь могут быть замещены в формулу для одного образца в соотношении Z-интервале:
{ displaystyle { hat {p}} = 0,68}{ displaystyle n = 400}{ displaystyle z ^ {*} = 1,96}

{ displaystyle { hat {p}} pm z ^ {*} { sqrt { frac {{ hat {p}} (1 - { hat {p}})} {n}}} Rightarrow (0,68) pm (1,96) { sqrt { frac {(0,68) (1-0,68)} {(400)}}} Rightarrow 0,68 pm 1,96 { sqrt {0,000544}}} { displaystyle Rightarrow { bigl (} 0,63429,0.72571 { bigr)}}

Основываясь на условиях вывода и формуле для доли одной выборки в интервале Z, с уровнем достоверности 95% можно сделать вывод, что процент населения избирателя в этой демократии, поддерживающей кандидата B, составляет от 63,429% до 72,571. %.

Значение параметра в диапазоне доверительного интервала

Часто задаваемый вопрос в выводной статистике – входит ли параметр в доверительный интервал. Единственный способ ответить на этот вопрос – провести перепись. Ссылаясь на приведенный выше пример, вероятность того, что доля населения находится в диапазоне доверительного интервала, равна либо 1, либо 0. То есть, параметр включен в диапазон интервала или нет. Основная цель доверительного интервала – лучше проиллюстрировать, каким может быть идеальное значение параметра.

Распространенные ошибки и неверные толкования оценок

Очень распространенная ошибка, возникающая при построении доверительного интервала, – это убеждение, что уровень достоверности, например , означает 95% -ный шанс. Это неверно. Уровень уверенности основан на степени достоверности, а не вероятности. Следовательно, значения попадают исключительно в интервал от 0 до 1.
{ displaystyle C = 95 %}C

Оценка P с использованием выборки из ранжированного набора

Более точную оценку P можно получить, выбрав выборку из ранжированного набора вместо простой случайной выборки.

Смотрите также

  • Доверительный интервал биномиальной пропорции
  • Доверительный интервал
  • Распространенность
  • Статистическая проверка гипотез
  • Статистические выводы
  • Статистический параметр
  • Интервал допуска

использованная литература

Источник

Добавить комментарий