Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
|
| Дуга |  |
|
| Круг |  |
|
| Сектор |  |
|
| Сегмент |  |
|
| Правильный многоугольник |  |
|
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
 ,
,
где R – радиус круга, D – диаметр круга
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
|
| Площадь сектора |  |
|
| Площадь сегмента |  |
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Сегмент круга
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент круга
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Как найти часть от площади окружности
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
[spoiler title=”источники:”]
http://planetcalc.ru/1421/
http://izamorfix.ru/matematika/planimetriya/krug.html
[/spoiler]
Основными параметрами, которыми измеряется круг, являются его радиус, площадь и длина окружности. Найти какую-то долю – например, две трети – от каждой из этих величин можно путем простейших вычислений. Но иногда возникает необходимость выделить на нарисованном круге «дольку», величиной в те же две трети его площади. Такую долю круга обычно называют сектором – его образуют два радиуса и дуга окружности. Выделить такой сектор можно вообще без каких-либо вычислений.

Вам понадобится
- Бумага, циркуль, транспортир, линейка.
Инструкция
Если в вашем распоряжении есть нарисованный круг и циркуль, выделить на этом рисунке две трети будет несложно. Отложите на циркуле радиус круга и установите иглу в любую точку окружности, т.е. границы круга. Сделайте отметки на окружности в обе стороны от выбранной на ней точки. Эти две отметки делят линию, ограничивающую круг, на две дуги. Длина большей из них равна двум третям длины периметра, а значит задача решена. Вы можете начертить прямые линии, соединяющие эти точки с центром, если в условиях требуется нарисовать сектор размером в две трети круга.
Циркуль можно заменить транспортиром и линейкой. В этом случае сначала поставьте в любом месте окружности точку – это будет одна из границ, разделяющих две дуги. Затем приложите транспортир к прямой, проходящей через эту точку и центр круга, таким образом, чтобы нулевая отметка совпадала с центром фигуры. Поставьте вспомогательную точку напротив отметки в 120°. Затем с помощью линейки отметьте пересечение с окружностью луча, начинающегося в центре круга и проходящего через вспомогательную точку. Это пересечение будет второй границей, разделяющей две дуги – большая из них будет равна двум третям окружности. Останется лишь провести два радиуса, если нужно рисовать на чертеже сектор.
При необходимости не начертить, а только рассчитать величину (l), равную двум третям длины окружности, необходимо знать диаметр круга (D). Длина всей границы этой фигуры равна произведению диаметра на число Пи, поэтому для получения ответа умножайте эту величину на две трети: l = ⅔*π*D.
Для вычисления площади сектора (s), равного двум третям круга, удобнее вместо диаметра использовать его половину – радиус (R). Площадь всего круга равна произведению того же числа Пи на радиус, возведенный в квадрат. Для расчета площади нужного сегмента найдите две трети от этой величины: s = ⅔*π*R².
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Площадь сегмента круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь сегмента круга
Чтобы посчитать площадь сегмента круга воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
По углу и радиусу

Угол α =
Радиус r =
Площадь сегмента круга
Sск =
0
Округление ответа: Округление числа π:
По длине хорды и высоте сегмента
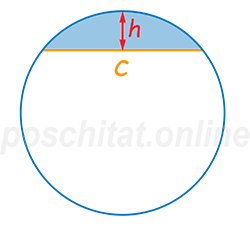
Хорда c =
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
По высоте и радиусу (или диаметру)

=
Высота сегмента h =
Площадь сегмента круга
Sск =
0
Округление ответа:
Просто введите данные и получите ответ.
Теория
Площадь сегмента окружности через угол и радиус
Чему равна площадь сегмента окружности Sск, если её радиус r, а угол сегмента α ?
Формула
В градусах:
Sск = r²2 ⋅ (π ⋅ α180° – sin α)
В радианах:
Sск = r²2 ⋅ (α – sin α)
Пример
К примеру, посчитаем площадь сегмента круга, имеющего радиус r = 2 см, а угол сегмента ∠α = 45°:
Sск = 2²2 ⋅ (3.14 ⋅ 45180 – sin 45) = 2 ⋅ (0.785 – 0.707) = 0.156 см²
Площадь сегмента окружности через хорду и высоту сегмента
Чему равна площадь сегмента окружности Sск, если длина хорды c, а высота сегмента h ?
Чтобы посчитать площадь сегмента, нам для начала потребуется вычислить радиус окружности r и угол сегмента α. А затем воспользоваться формулой площади сегмента из предыдущего параграфа.
Формула
Радиус круга:
r = c² + 4h²8h
Угол сегмента:
∠α = 2 ⋅ arcsinc2r
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 2 см и длину хорды c = 5 см:
r = 5² + 4⋅2²8⋅2 = 25 + 1616 = 2.5625 см∠α = 2 ⋅ arcsin52 ⋅ 2.5625 = 2 ⋅ arcsin 0.9756 ≈ 2.7 radSск = 2.5625²2 ⋅ (2.7 – sin 2.7) = 3.2832 ⋅ (2.7 – 0,427) = 7.46 см²
Площадь сегмента окружности через высоту и радиус (или диаметр)
Чему равна площадь сегмента окружности Sск, если его высота h, а радиус r ?
Если нам известен не радиус, а диаметр, то делим его на 2 и получаем радиус (r = d ÷ 2).
Далее нам остаётся определить угол сегмента α. А затем воспользоваться формулой площади сегмента, описанной выше.
Формула
Угол сегмента:
∠α = 2 ⋅ arccosr – hr
Пример
К примеру, посчитаем площадь сегмента круга, имеющего высоту h = 1 см, а диаметр окружности d = 4 см:
r = 4 ÷ 2 = 2 см
∠α = 2 ⋅ arccos2 – 12 = 2 ⋅ arccos 0.5 = 2.094 radSск = 2²2 ⋅ (2.094 – sin 2.094) = 2 ⋅ (2.094 – 0.866) = 2.456 см²
См. также
![]()
Здравствуйте, друзья! В состав ЕГЭ по математике входят задачи связанные с нахождением площади круга или его частей (сектора, кольцевых элементов). Фигура задаётся на листе в клетку. В одних задачах масштаб клетки задаётся 1×1 сантиметр, в других он не оговаривается – даётся площадь элемента круга или самого круга.
Задания неглубокие, необходимо помнить формулу площади круга, уметь визуально (по клеткам) определить радиус круга, какую долю от круга составляет выделенный сектор. Кстати, на блоге имеется статья о площади сектора. Её содержание к решению представленных ниже задач отношения не имеет, но для тех, кто хочет вспомнить формулу площади круга и площади сектора будет весьма полезна. Рассмотрим задачи (взяты из открытого банка заданий):

Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Для того, чтобы площадь фигуры (кольца) необходимо из площади круга радиусом равным 2 вычесть площадь круга с радиусом 1. Формула площади круга:
![]()
Значит,
![]()
Разделим результат на число Пи и запишем ответ.
Ответ: 3

На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

Площадь заштрихованной фигуры можно найти вычислив разность между площадью большего круга и площадью меньшего. Определим во сколько раз площадь большего отличается от площади меньшего. Пусть радиус меньшего равен R, тогда его площадь равна:
![]()
Радиус большего круга в два раза больше (видно по клеткам). Значит, его площадь равна:
![]()
Получили, что его площадь в 4 раза больше.
Следовательно, она равна 51∙4 = 204 см2
Таким образом, площадь заштрихованной фигуры равна 204 – 51 = 153 см2.
*Второй способ. Можно было вычислить радиус малого круга, затем определить радиус большего. Далее найти площадь большего и вычислить площадь искомой фигуры.

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

Данная задача по ходу решения практически не отличается от предыдущей, разница состоит лишь в том, что круги имеют разные центры.
Несмотря на то, что видно, что радиус большего круга в 2 раза больше радиуса меньшего, советую вам обозначить размер клетки переменной х (икс).
Так же, как и в предыдущей задаче, определим во сколько раз площадь большего отличается от площади меньшего. Выразим площадь меньшего круга, так как его радиус равен 3х:
![]()
Выразим площадь большего круга, так как его радиус равен 6х:
![]()
Как видно, площадь большего круга в 4 раза больше.
Следовательно, она равна 1∙4 = 4 см2
Таким образом, площадь заштрихованной фигуры равна 4 – 1 = 3 см2.
Ответ: 3

На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Обозначим размер клетки переменной х (икс).
Определим во сколько раз площадь большего круга отличается от площади меньшего. Выразим площадь меньшего круга. Так как его радиус равен 3∙х, то
![]()
Выразим площадь большего круга. Так как его радиус равен 4∙х, то
![]()
Разделим площадь большего на площадь меньшего:

То есть, площадь большего круга в 16/9 раза больше площади меньшего, следовательно, она равна:
![]()
Таким образом, площадь заштрихованной фигуры равна 16 – 9 = 7 см2.
*Второй способ.
Вычислим радиус меньшего круга. Его площадь равна 9, значит,

Найдём размер клетки и затем сможем определить радиус большего круга. Размер клетки равен:

Так как радиус большего круга соответствует 4 клеткам, то его радиус будет равен:

Определяем площадь большего круга:

Находим разность: 16 – 9 = 7 см2
Ответ: 7

На клетчатой бумаге нарисован круг площадью 48. Найдите площадь заштрихованного сектора.

В этой задаче очевидно, что заштрихованная часть составляет половину от площади всего круга, то есть равна 24.
Ответ: 24

На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?

По рисунку видно, что площадь сектора составляет треть от площади круга. Значит, площадь круга будет равна 32∙3 = 96.
Ответ: 96
![]()
Найдите (в см2) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см. В ответе запишите S/л.

Посмотреть решение
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/л.

Посмотреть решение
Небольшой итог.
В задачах связанных с площадью сектора круга необходимо уметь определять какую долю он составляет от площади круга. Это сделать не сложно, так как в подобных задачах центральный угол сектора кратен 30 либо 45.
В задачах связанных с нахождением площадей кольцевых элементов есть разные пути для решения, оба показаны в решённых заданиях. Способ, в котором размер клетки обозначается через переменную х, и затем определяются радиусы более универсален.
Но самое главное – не запоминать эти способы. Можно найти и третий и четвёртый путь решения. Главное – это знать формулу площади круга и уметь логически рассуждать.
На этом всё. Успеха вам!
С уважением, автор проекта Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Площадь круга, сектора
Разделим окружность на возможно большее число равных частей, все полученные точки деления соединим с центром окружности, а соседние — друг с другом хордами.
Таким образом получим ряд равных равнобедренных треугольников (черт. 339).
Площадь каждого треугольника равна ah /2, где а — основание его, h — высота.
Обозначив через S’ сумму площадей всех полученных треугольников, получим формулу:
Сумма площадей всех треугольников (S’) весьма близка к площади круга (S), сумма оснований всех треугольников (an) весьма близка к длине окружности (C), а высота (h) каждого треугольника весьма близка к радиусу (r) круга.
Если пренебречь незначительными различиями в размерах, то получим формулу площади круга:
После преобразования получим ( S_ = frac ), или Sкр = π r 2 ; а обозначив через D диаметр круга, получим:
$$ S_ = frac $$
Примечание. В формуле (S_ = frac) поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах доказывается, что равенство (S_ = frac) не приближённое, а точное.
Впишем в круг, радиус которого обозначим R, какой-нибудь правильный многоугольник.
Пусть площадь этого многоугольника будет q, периметр — р, апофема — а.
По формуле вычисления площади правильного многоугольника имеем:
Вообразим теперь, что число сторон этого многоугольника неограниченно удваивается. Тогда периметр р и апофема а (следовательно, и площадь q) будут увеличиваться, причём периметр будет стремиться к пределу, принимаемому за длину C окружности, апофема будет стремиться к пределу, равному радиусу R круга. Из этого следует, что площадь многоугольника, увеличиваясь при удвоении числа сторон, будет стремиться к пределу, равному 1 /2С • R. Предел этот принимается за численную величину площади круга. Таким образом, обозначив площадь круга буквой К, можем написать:
т. е. площадь круга равна половине произведения длины окружности на радиус.
Так как С = 2πR, то
т. е. площадь круга равна квадрату радиуса, умноженному на отношение длины окружности к диаметру.
Следствие. Площади кругов относятся, как квадраты радиусов или диаметров.
Действительно, если K и K1 будут площади двух кругов, a R и R1 — их радиусы, то
Площадь сектора
Сектором называется часть круга, ограниченная двумя радиусами и дугой. На чертеже 340 сектор AOB заштрихован.
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Получаем формулу:
$$ S = frac $$ где S — площадь сектора.
Почему площади кругов относятся как квадраты их радиусов?
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 12. Найдите площадь закрашенной фигуры.
—->Площади кругов относятся как квадраты их радиусов<—-
Поскольку радиус большего круга в 5 раза больше радиуса меньшего круга, площадь большего круга в 25 раз больше площади меньшего. Следовательно, она равна 300. Площадь заштрихованной фигуры равна разности площадей кругов: 300 − 12 = 288.
(P.S) Мне в гугле выдало только Киселёва, но там ничего не понял, а в моём учебнике нету, давно было.
Существует квадрат со стороной 2R, в который вписывается круг радиусом R.
При этом круг всегда занимает конкретную долю площади квадрата, равную п/4.
Площадь квадрата равна произведению его сторон:
Sкв = 2R • 2R = 4R²
Площадь круга равна известной доле от площади квадрата:
Sкр = п/4 • Sкв = п/4 • 4R² = пR²
Итак, мы видим, что площадь круга прямо пропорциональна квадрату его радиуса.
