-
-
December 3 2013, 23:24
Listens: Tequilajazzz – Двойники – 2002 Выше осени
- Наука
- Cancel
Вероятность как доля
Вот по моему опыту общения со студентами-околобиологами, теорвер часто воспринимается как нечто довольно отвлеченное. Хотя, пожалуй, это – один из наиболее “посюсторонних” разделов математики. Уж по крайней мере в тех основах, которым обучают нематематиков.
В частности, всякие понятия условной вероятности и сопутствующие формулы полной вероятности и Байеса – простые до икоты, вообще говоря – часто вызывают существенные затруднения. Ибо они тупо заучиваются, хотя их, по-хорошему, надо каждый раз выводить здравым смыслом.
Думается мне (и проверяется на школьничках), что помочь тут может представление о вероятности как о доле. В конце концов, что есть вероятность, как не доля? Вспомните классическое определение: вероятность есть доля благоприятных исходов в общем их числе. Все остальные определения, на самом деле, восходят к этому.
Был, кстати, такой австрияк Рихард фон Мизес, который развивал “частотный подход” к вероятности. В итоге все математики радостно приняли аксиоматическое определение Колмогорова – оно действительно более легко формализуемо (там вероятность рассматривается как мера на пространстве элементарных событий – уже же стращно звучит, да?). Но даже сам Андрей Николаевич признавал важность подхода Мизеса для практических применений. Книжка фон Мизеса Wahrscheinlichkeit, Statistik und Wahrheit (в русском переводе почему-то “Вероятность и статистика”, а не “Вероятсноть, статистика и истина”) переведена на русский – весьма интересная, кстати, помогает осознать, что есть вероятность.
И во всяких практических задачках вероятность чаще всего и знаменует собою долю. Вот есть в задачке “Стрелок попадает в цель с вероятностью 70%” – это же значит, что из всех выстрелов стрелка успешными оказываются 70%. “Насекомое несет мутацию Х с вероятностью 25%” = “25% насекомых несут мутацию Х”.
В конце концов, мы рассчитать значение конкретной вероятности никак иначе и не можем, кроме как оценив ее как долю.
Так вот, возвращаясь к разъяснению теорвера. Если простенькие задачки по теории вероятностей переформулировать в терминах долей, они, думаю, станут многим понятнее. В конце концов понятные доли – это не какие-то непонятные вероятности.
А часто вызывающее затруднение понятие “условной вероятности” – это же лишь доля от доли!
Вот такой пример мы со школьничками разбирали:
“Вероятность того, что пойдет дождь, равна в день с солнечным утром 5%, а в день с пасмурным утром – 50%. Вероятность того, что утром пасмурно, – 25%. 1)Какова вероятность, что в наугад выбранный день пойдет дождь? 2) Какова вероятность, что в дождливый день утро было пасмурным?”
И – вариант с долями:
“Дождь идет в 5% ото всех дней с солнечным утром и в 50% дней с пасмурным утром. 25% всех дней – с пасмурным утром. 1)В какую долю ото всех дней идет дождь? 2) Какова доля дней с пасмурным утром среди дождливых дней?”
Внимание, вопрос к тем, кто с теорвером незнаком и лицам, приравненным к ним: понятнее ли вторая формулировка?
Пусть требуется оценить долю тех
объектов заданной генеральной
совокупности, которые удовлетворяют
некоторому условию
– генеральную долю
.
Для этого из генеральной совокупности
выделяют выборку, и по результатам её
обследования находят долю тех объектов,
которые удовлетворяют условию
– выборочную долю
.
Очевидно, что
,
где
– объем выборки,
– число тех её объектов, которые
удовлетворяют условию
.
Выборочная доля в данном случае является
той величиной, с помощью которой мы
получим информацию о неизвестном
значении генеральной доли.
Таким образом, выборочная доля
является
оценкой генеральной доли
.
Пример.
– доля бракованных деталей генеральной
совокупности,
– доля бракованных деталей в выборке.
Условие (событие)
– деталь, взятая наудачу из генеральной
совокупности – бракована.
Простейший способ оценивания – точечное
оценивание – подразумевает использование
приближенного равенства
.
Как и всякая оценка, выборочная доля
является случайной величиной.
Действительно, выборка из генеральной
совокупности выделяется случайным
образом. Соответственно то значение,
которое примет выборочная доля, будет
случайным.
Следующие теоремы характеризуют
выборочную долю как случайную величину.
Теорема 1. Математическое ожидание
выборочной доли равно генеральной доле:
.
Среднее квадратическое отклонение
(
)
выборочной доли вычисляется по формулам
– в случае повторной выборки и
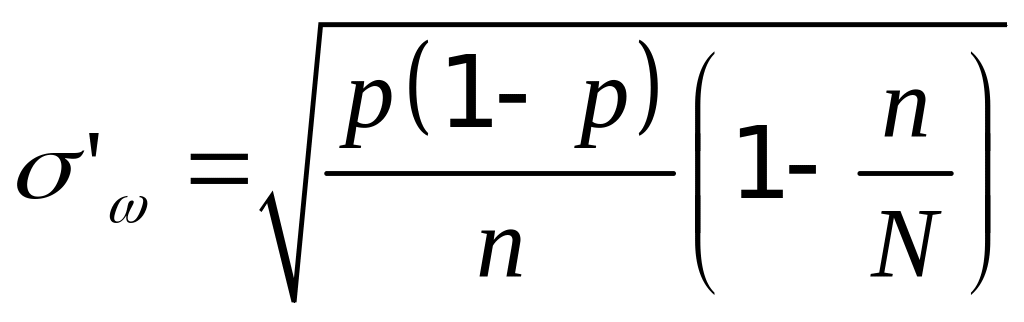
– в случае бесповторной выборки, где
–
объем генеральной совокупности.
Напомним, что по определению среднего
квадратического отклонения в случае
повторной выборки имеем
(аналогично в случае бесповторной
выборки).
Замечание. При применении формул
Теоремы 1 полагают
.
Теорема 2. Закон распределения
выборочной доли неограниченно приближается
к нормальному закону при неограниченном
увеличении объема выборки.
Подобно тому, как мы это сделали в
предыдущем параграфе, как следствие
Теоремы 2, получаем формулу доверительной
вероятности:
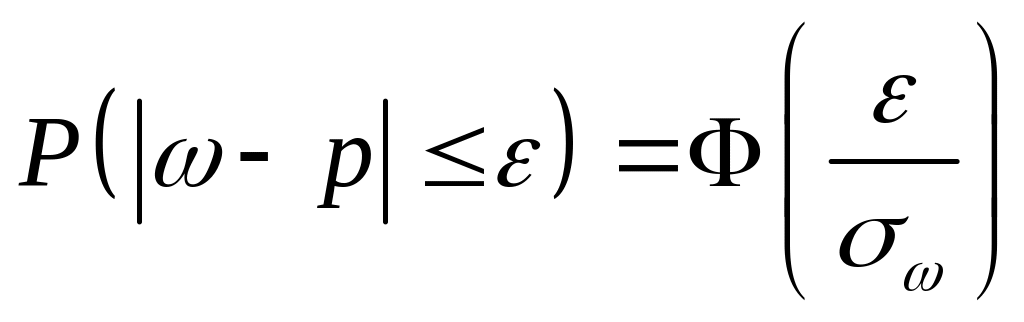
– в случае повторной выборки. Заменяя
в последнем равенстве
на
,
получаем формулу доверительной
вероятности в случае бесповторной
выборки.
По определению, величина
,
фигурирующая в формуле доверительной
вероятности, называется предельной
ошибкой выборки. Интервал
называется доверительным интервалом.
Выше было указано, в чем состоит точечная
оценка генеральной доли. Интервальное
оценивание сводится, например, к
вычислению значения доверительной
вероятности при заданной предельной
ошибке выборки.
Теорема 3. В случае повторной
выборки выборочная доля является
несмещенной и состоятельной оценкой
генеральной доли.
Пример. Выборочные данные о надое
молока для 100 коров из 1000 представлены
таблицей:
-
Надой молока,
ц10-20
20-30
30-40
40-50
50-60
Число коров
2
18
46
30
4
100
-
Найти вероятность того, что доля всех
коров с надоем молока более 40 ц отличается
от такой доли в выборке не более чем на
0,05 (по абсолютной величине), для случая
повторной и бесповторной выборок. -
Найти границы, в которых с вероятностью
0,9596 заключена доля всех коров с надоем
более 40 ц. -
Сколько коров надо обследовать, чтобы
с вероятностью 0,9786 для генеральной
доли коров с надоем более 40 ц можно было
гарантировать те же границы что и в
п.2.
Решение. Число
коров с надоем более 40 ц равно 34 (
,
см. заданный вариационный ряд). Тогда
.
Для нахождения доверительной
вероятности п. 1 задания воспользуемся
одноименной формулой при
.
Пусть рассматриваемая выборка –
повторная. Тогда по формуле Теоремы 1,
учитывая Замечание, получаем
.
Следовательно
.
Аналогично, в случае бесповторной
выборки:
,
.
Доверительным в данном случае является
интервал
.
Таким образом, неизвестное значение
доли всех коров с надоем более 40 ц
накрывается доверительным интервалом
(0,29;0,39) с вероятностью 0,7109 в случае
повторной выборки и с вероятностью
0,733 в случае бесповторной выборки.
В п. 2 задания при заданном значении
доверительной вероятности искомым
является доверительный интервал.
Поскольку значение выборочной доли
известно, остается найти предельную
ошибку выборки
.
Пусть выборка – повторная. По условию,
принимая во внимание формулу доверительной
вероятности, имеем
.
По таблице значений функции Лапласа
найдем такое
,
что
:
.
Тогда
и, используя найденное выше значение
,
получаем
.
Соответственно, доверительным будет
интервал:
.
Пусть выборка – бесповторная. Аналогично
предыдущему, получаем предельную ошибку
выборки
и доверительный интервал:
.
Таким образом, доля всех коров с надоем
молока более 40 ц с вероятностью
0,9596 накрывается доверительным
интервалом (0,243; 0,437) в случае повторной
выборки и интервалом (0,248; 0,432) в
случае бесповторной выборки.
В п. 3 по заданным значениям доверительной
вероятности и предельной ошибки выборки
найдем необходимый объем выборки. Из
начла решения заимствуем значение
выборочной доли
,
найденное по исходному вариационному
ряду.
Пусть выборка – повторная. По условию,
принимая во внимание формулу доверительной
вероятности, имеем:
.
По таблице значений функции Лапласа
найдем такое
,
что
:
.
Тогда
и,
.
Подставляя вместо
выражение из Теоремы 1, приходим к
уравнению относительно неизвестной
величины
:
.
Решая это уравнение относительно
,
подставляя в полученную формулу известные
величины, завершаем решение
(заметим, что, как и ранее, округление
здесь произведено в большую сторону).
Аналогично, в случае бесповторной
выборки из условия и формулы доверительной
вероятности следует равенство
или, принимая во внимание известное
выражение для
(см. Теорему 1):
.
Решая это уравнение относительно
,
получаем
.
Подставляя в правую часть последнего
равенства известные значения, окончательно
имеем:
.
Таким образом, в повторную выборку
надо взять 127 коров, чтобы с вероятностью
0,9786 можно было утверждать, что доля
всех коров с надоем молока более 40 ц
накрывается доверительным интервалом
(0,243; 0,437). Аналогично, в бесповторную
выборку надо взять 123 коровы, чтобы
с вероятностью 0,9786 можно было
утверждать, что доля всех коров с
надоем молока более 40 ц накрывается
доверительным интервалом (0,248; 0,432).
Домашнее задание: 9.19, 9.21, 9.23,
9.30.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 16 мин Просмотров 126к. Опубликовано 25 мая, 2018
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда
Вероятность подходящих событий + вероятность неподходящих событий = 1
Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Содержание
- Вероятность нескольких событий
- Задачи и решения задач на вероятность
- Вероятность нескольких событий
- Дополняющая вероятность
Вероятность нескольких событий
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем.
Задачи и решения задач на вероятность
Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.
Решение:
Вероятность, это отношение благоприятных вариантов к общему их количеству.
Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.
Вероятность тогда:
Ответ: 0,8.
Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?
Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.
Вероятность что первый дежурный мальчик:
Вероятность что второй дежурный мальчик:
Раз оба должны быть мальчики, вероятности перемножим:
Ответ: 0,2.
Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.
Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.
Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.
Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.
Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.
Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).
Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.
Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.
Задача 10.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.
Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?
Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.
Задача 11.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.
Задача 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.
Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.
Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.
Вероятность нескольких событий
Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Решение:
Тип вопроса: совмещение событий.
Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.
Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
| Игра №1 | Игра №2 | Вероятность данного варианта |
| 3 | 1 | 0,4 · 0,2 = 0,08 |
| 1 | 3 | 0,2 · 0,4 = 0,08 |
| 3 | 3 | 0,4 · 0,4 = 0,16 |
Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.
Решение:
Тип вопроса: уменьшение групп.
Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.
Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение:
Способ №1
Тип задачи: уменьшение групп.
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.
Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют в несколько вариантов:
Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Тип задачи: уменьшение групп.
Способ №1
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:
Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:
Орёл ― решка ― орёл;
Орёл ― орёл ― решка;
Решка ― орёл ― орёл;
Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)
Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.
Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Тип вопроса: совмещение событий.
В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.
Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
Тип вопроса: совмещение событий.
Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.
Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.
Решение:
Тип вопроса: совмещение событий.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):
… США, КАН, КИТ …
… США, КИТ, КАН …
… КИТ, США, КАН …
… КАН, США, КИТ …
… КАН, КИТ, США …
… КИТ, КАН, США …
США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:
≈ 0,33.
Дополняющая вероятность
Задача 1.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.
Найдите вероятность того, что случайно выбранная батарейка будет забракована.
Решение:
Существуют 2 варианта, которые нам подходят:
Вариант А: батарейка забракована, она неисправна;
Вариант Б: батарейка забракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;
Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;
Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.
Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение:
Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).
Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.
Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.
Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.
Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.
Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.
Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.
Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.
Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):
| 11 апреля | 12 апреля | 13 апреля | Вероятность данного варианта |
| X – 0,9 | X – 0,9 | O – 0,1 | 0,9 ·0,9 ·0,1 = 0,081 |
| X – 0,9 | O – 0,1 | O – 0,9 | 0,9 ·0,1 ·0,9 = 0,081 |
| O – 0,1 | O – 0,9 | O – 0,9 | 0,1 ·0,9 ·0,9 = 0,081 |
| O – 0,1 | X – 0,1 | O – 0,1 | 0,1 ·0,1 ·0,1 = 0,001 |
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.
Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):
| 4 июля | 5 июля | 6 июля | Вероятность данного варианта |
| X – 0,8 | X – 0,8 | O – 0,2 | 0,8 · 0,8 · 0,2 = 0,128 |
| X – 0,8 | O – 0,2 | O – 0,8 | 0,8 · 0,2 · 0,8 = 0,128 |
| O – 0,2 | O − 0,8 | O − 0,8 | 0,2 · 0,8 · 0,8 = 0,128 |
| O – 0,2 | X – 0,2 | O – 0,2 | 0,2 · 0,2 · 0,2 = 0,008 |
Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.
Сообщения без ответов | Активные темы | Избранное
|
|
Интерпретация вероятности как доли: имеет ли смысл?
|
|
28/07/19 |
В этом сообщении пойдёт речь о самодельной интерпретации понятия вероятности; эту интерпретацию я придумал из своей головы, чтобы лично мне было удобнее усваивать настоящую теорию вероятности. Мне кажется, что стало удобнее; но мне хотелось бы узнать мнение специалистов о том, насколько мои измышления осмысленны. Считаю нужным предупредить, что я не претендую ни на какое новое слово в науке, а всего лишь прошу помочь мне разобраться, корректно ли моё понимание. Итак, в моей самодельной интерпретации всякая вероятность (вероятностная мера) понимается как доля меры , то есть отношение меры некоторого множества a к мере его надмножества A ; либо оценка этой доли (например, через предел), если сама доля почему-либо недоступна. Например:
Во всех подобных случаях я считаю важным то, что вероятность — не просто отношение какой-то меры к какой-то другой, а именно отношение меры множества к мере его же надмножества. Также допускаю, что интерпретация может быть верной в случае, если одна или обе этих меры сами по себе не существуют или недоступны, но их отношение всё равно имеет смысл. (Правда, не могу придумать никакого примера для этого случая.) Соответственно, вопросы:
|
|
|
|
|
VPro |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
16/02/10 |
Вы геометрическую и частотную вероятности обозвали одним словом. Но понятие вероятностной меры гораздо шире. Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины.
|
|
|
|
|
upgrade |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
07/08/14 |
отношение меры некоторого множества a к мере его надмножества A А как бы вы тогда назвали обратное отношение (которое всегда
|
|
|
|
|
arseniiv |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
27/04/09 |
-_- Вспомните условную вероятность Заодно видно, когда будут проблемы: если мера какого-то множества бесконечна или ноль, вы не сможете такой конструкцией получить вероятностное пространство (нельзя получить нормированную меру). Надо чтобы в исходном пространстве с мерой мера А как бы вы тогда назвали обратное отношение (которое всегда Раз есть кепстр , может быть и оревятность . Хотя толку от такой вещи наверно нет.
|
||
|
|
|||
|
-_- |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
28/07/19 |
Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины. Доля площади под кривой соответствующей функции плотности распределения. — 19.08.2019, 18:14 — А как бы вы тогда назвали обратное отношение (которое всегда А разве в общепринятой теории вероятности как-то специально рассматривается величина, обратная вероятности? — 19.08.2019, 18:29 — -_- Вспомните условную вероятность Возможно, я чего-то недопонимаю; собственно, я и открыл эту тему в надежде на то, чтобы разобраться, чего именно. Но я не вижу, в чём разница моей интерпретации для условной вероятности по сравнению с «безусловной». Вы сами пишете, что условная вероятность — это то же самое, что просто вероятность, но в другом вероятностном пространстве. С бесконечной или нулевой мерой я тоже пока не разглядел проблем. Я был бы вам признателен за конкретный пример типа такого: в таком-то конкретном случае общепринятая теория вероятности говорит, что такая-то вероятность равна X , но в моей интерпретации через «долю меры» для этого случая нельзя указать таких множеств a и A и такой меры, чтобы доля меры a от меры его надмножества A составляла именно X .
|
|
|
|
|
upgrade |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
07/08/14 |
А разве в общепринятой теории вероятности как-то специально рассматривается величина, обратная вероятности? Я не настолько хорошо знаю теорвер. (В расчетах встречается)
|
|
|
|
|
mihaild |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
16/07/14 |
Но для “компьютера” удобнее писать так: Не надо так писать. Что если
|
||
|
|
|||
|
arseniiv |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
27/04/09 |
Вы сами пишете, что условная вероятность — это то же самое, что просто вероятность, но в другом вероятностном пространстве. Так в том и дело, что вы по сути предлагаете определять вероятность как условную вероятность («условную меру») событий—подмножеств данного
|
||
|
|
|||
|
upgrade |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
07/08/14 |
(mihaild) Не надо так писать. Что если То есть, когда все три события точно произойдут – какова вероятность того, что произойдет ровно одно событие…тут я пас, ибо “правильная” формула говорит, что вероятность такая равна нулю, а “неправильная, но удобная” начинает создавать проблемы, которые решаются “ломом” – в программе пишется, что “если так, то пусть будет
|
|
|
|
|
VPro |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
16/02/10 |
Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины. Доля площади под кривой соответствующей функции плотности распределения. Для шутки сойдет. У Вас еще нет никакой функции распределения, Вам ее только задать нужно. Плотность откуда взялась? А если, скажем ее нет вовсе?
|
|
|
|
|
-_- |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
28/07/19 |
Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины. Для шутки сойдет. У Вас еще нет никакой функции распределения, Вам ее только задать нужно. Простите, я вас не понимаю. В предыдущем сообщении вы просили дать «интерпретацию функции распределения непрерывной случайной величины», а теперь пишете, что «нет никакой функции распределения». Так функция есть или нет?
|
|
|
|
|
Евгений Машеров |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
11/03/08 |
Э… Было 6 умножений, 2 сложения.
|
||
|
|
|||
|
VPro |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
|
16/02/10 |
Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины. Для шутки сойдет. У Вас еще нет никакой функции распределения, Вам ее только задать нужно. Простите, я вас не понимаю. В предыдущем сообщении вы просили дать «интерпретацию функции распределения непрерывной случайной величины», а теперь пишете, что «нет никакой функции распределения». Так функция есть или нет? Хорошо, вы не поняли вопроса. Бывает. Но Вы же не можете не понимать, что задавать функцию распределения через плотность этого распределения это нелепо?
|
|
|
|
|
Brukvalub |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
01/03/06 |
-_- , я уверен, что гениальность Колмогорова позволила ему создать столь совершенную математическую модель для понятия “вероятность”, что эта модель не нуждается в каких-либо новых интерпретациях. Если не получается понять аксиоматику Колмогорова, то разумнее всего честно сказать себе: “теория вероятности мне не по уму”, бросить заниматься теорией вероятности и заняться чем-нибудь другим.
|
||
|
|
|||
|
arseniiv |
Re: Интерпретация вероятности как доли: имеет ли смысл?
|
||
27/04/09 |
Если ТС только начал, то пускай ещё попытается несколько раз. Ну и может он ожидает какого-то волшебного понимания, когда достаточно обычного. -_- Кстати, какие книги вы изучаете по этой теме? (Скорее всего я ничего о них сказать не смогу, но кто-то другой — вероятнее.) Может, вы выбрали неудачную, это случается.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Stepan-S |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
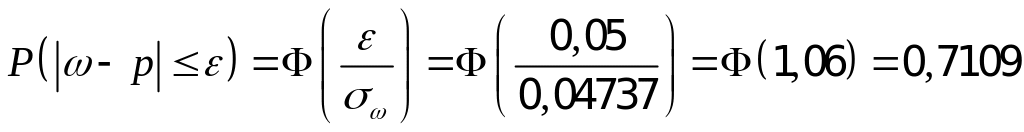
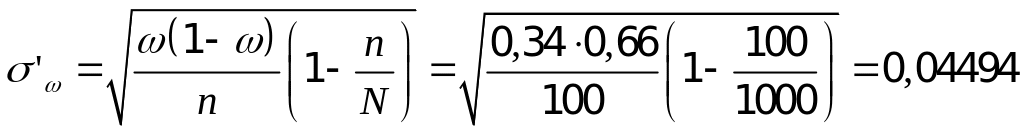
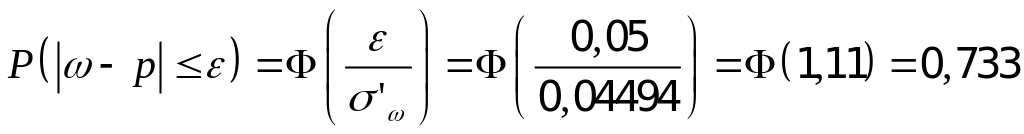
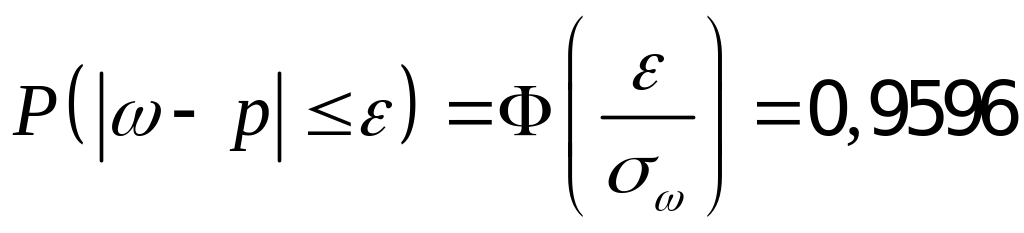
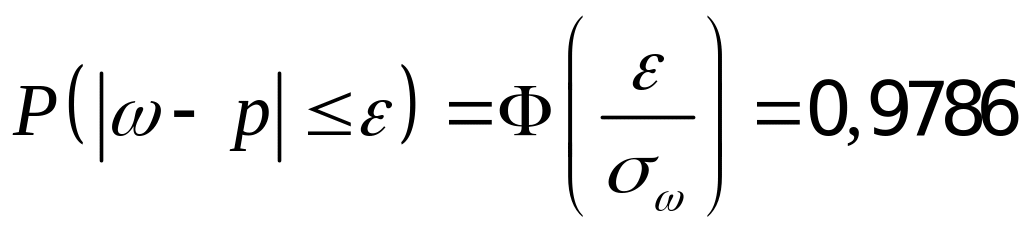
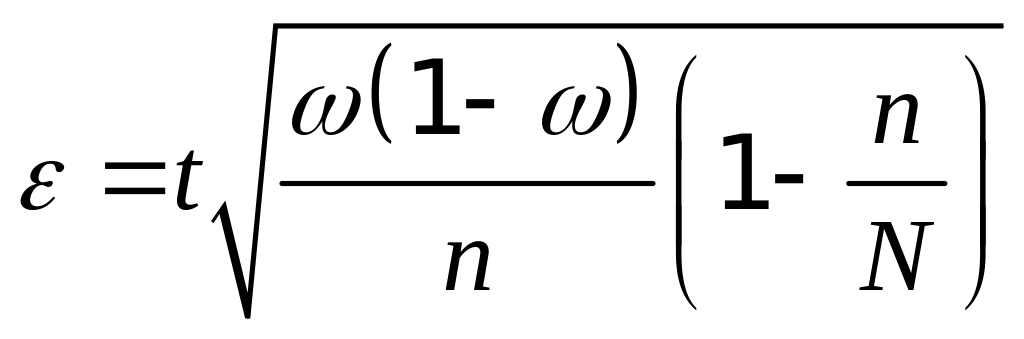
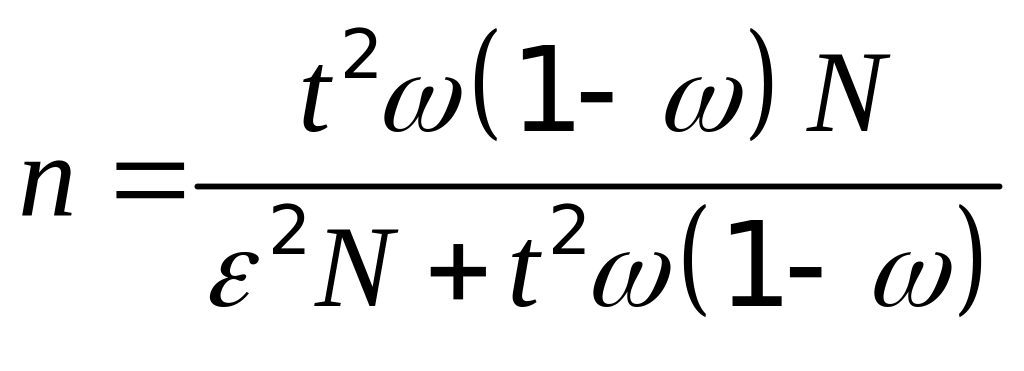
 .
. ?
? — это обычная вероятность
— это обычная вероятность  в «вероятностном подпространстве», где множество элементарных исходов —
в «вероятностном подпространстве», где множество элементарных исходов —  , из алгебры событий выкинуты все множества
, из алгебры событий выкинуты все множества  (проверьте, что этот набор множеств будет сигма-алгеброй!), а мера оставшихся умножена на константу, чтобы была нормированной (проверьте, что это будет мера). Так что любую вероятность можно рассматривать как условную и любую условную вероятность можно рассматривать как просто вероятность — просто всё в разных пространствах.
(проверьте, что этот набор множеств будет сигма-алгеброй!), а мера оставшихся умножена на константу, чтобы была нормированной (проверьте, что это будет мера). Так что любую вероятность можно рассматривать как условную и любую условную вероятность можно рассматривать как просто вероятность — просто всё в разных пространствах. ,
, ?
? “.
“.
