Если известно сколько составляет часть от целого, то по известной части можно “восстановить”
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
![]()
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
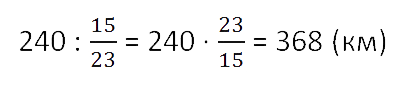
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
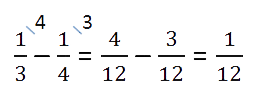
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
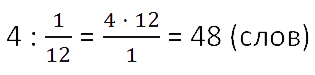
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Если известно сколько составляет часть от целого, то по известной части можно «восстановить»
целое.
Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).
Запомните!
![]()
Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.
Пример. Рассмотрим задачу.
Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?
Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет
часть пути.
240 : 15 = 16 (км)
Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью
.
Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:
16 · 23 = 368 (км)
Кратко запись решения такой задачи можно сделать следующим образом.
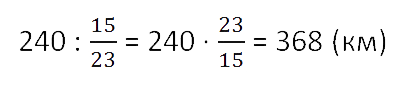
Ответ: поезд должен пройти 368 км.
Сложные задачи на нахождение числа по его части
Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.
Рассмотрим задачу.
При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?
Решение. Как обычно подчеркнём в условии задачи все важные данные.
Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.
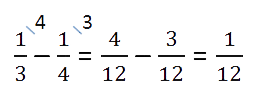
Такую часть всех слов составляют 4 слова.
Итак, 4 слова — это
от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь
.
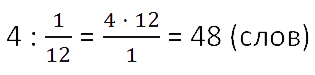
Ответ: всего 48 слов надо было выучить к диктанту.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
![]()
Альпинист собрался взобраться на пик высотой 5000 м. В первый день он преодолел 30% маршрута, а во второй день — на 20% больше, чем в первый. Определите, какую часть маршрута составляет пройденный путь от запланированного.
![]()
Сначала надо найти, сколько альпинист прошел в первый день пути.
Для этого узнаем, сколько приходится на 1%, для этого 5000 : 100% = 50 м — это 1 %.
Находим, сколько он прошел в первый день, для этого 50*30 = 1500 м. он прошел в первый день.
Узнаем, на сколько больше прошел, нам известно, что на 20% больше, чем в первый. Опять ищем 1 % — 1500:100 = 15 м, значит 20*15 = 300 м. на это расстояние больше. Теперь надо узнать, сколько всего во второй день прошел, для этого 1500+300 = 1800 м.
Высчитываем, сколько всего пройдено в первый и второй день: 1500+1800=3300 м всего пройдено.
Теперь высчитываем процент пройденного пути, для этого 3300/5000 = 0,66, умножаем на 100% = 66%.
Ответ: 66% от общего пути.
система выбрала этот ответ лучшим
Натишка2210
[36.3K]
4 года назад
Задача решается в несколько действий.
1) узнаем, сколько преодолел альпинист в первый день. Составим пропорцию:
5000 м — 100%
х м. — 30%
х= 5000*30/100
х = 1500 м
2) узнаем, сколько метров преодолел альпинист на второй день.
Если он прошёл на 20% больше, чем в первый день, то пропорция будет выглядеть так:
1500 — 100%
х — 120%
х= 1500*120/100
х = 1800
3) просуммируем пройденный путь в первый и второй день.
Получается, что альпинист прошёл 1500+1800 м = 3300 м.
4) узнаем, какой процент 3300 составляет от всего пути:
5000 м — 100%
3300 м — х%
х = 3300*100/5000
х = 66%
Ответ: альпинист прошёл 66% от запланированного пути.
![]()
storus
[73.8K]
4 года назад
Нам известно, что в первый день восхождения на вершину альпинист осилил 30% маршрута, что составляет 1500 метров (5000*30/100=1500).
А во второй он смог подняться на 20% дальше, нежели в первый день. То есть на 20% больше, чем 1500 метров.
20% от 1500 составляют 300 метров.
Значит во второй день альпинист продвинулся на 1500+300=1800 метров.
Тогда за два дня восхождения было пройдёно 1500+1800=3300 метров.
Найдём, какую часть от запланированного составляет пройдённый путь, составив пропорцию:
5000 — 100%
3300 — х
х=3300*100/5000=66%
Ответ: пройдённый за два дня путь составляет 66% от полной длины маршрута.
![]()
Master-Margarita
[135K]
4 года назад
Решение:
1) 5000 м * 0,3 = 1500 м — столько альпинист прошел в первый день (0,3 соответствует 30 %)
2) 1500 м * 1,2 = 1800 м. — столько альпинист прошел во второй день (на 20 % больше, чем в 1-й, поэтому к 1 добавляем 0,2)
3)1500 м + 1800 м = 3300 м. — столько альпинист прошел за два дня вместе.
4) 3300 м : 5000 м = 0,66, что соответствует 66 %.
Ответ: 66 %.
Для начала, нам следует посчитать какой путь прошел альпинист в первый день составив пропорцию. 5000 умножаем на 30 и делим на 100 и получаем 1500. Затем, следует посчитать какой путь смог пройти альпинист во 2 день. Известно, что он прошел на 20% больше, а это означает:
1500 умножаем на 1,2 и получаем 1800.
Затем нам следует найти отношение пройденного маршрута к изначальному:
(1500+1800) и делим на 5000 и получаем 0,66 = 66%.
Таким образом:
Ответ: Пройденный путь от запланированного составляет 66 процентов.
![]()
Лёля Про
[20.9K]
4 года назад
решение:
1) первым действием посчитаем, какой путь альпинист прошел в первый день:
Составим пропорцию:
5000 (м) = 100%
Х (м) = 30%
5000 * 30 / 100 = 1500 (м.)
2) вторым действием посчитаем какой путь прошел альпинист Во второй день:
Так как во второй день он прошел на 20% больше, значит:
1500 * 1,2 = 1800 (м.)
3) третьим действием найдем отношение пройденного маршрута к изначальному, для этого составим пример:
(1500 + 1800) / 5000 = 0,66 = 66%.
Ответ: 66% составляет пройденный путь от запланированного
Валентина МД
[33.2K]
4 года назад
Находим сколько метров прошёл альпинист в 1 день.
5000 (м) * 30/100 % = 1500 (м).
Находим сколько метров прошёл альпинист во 2 день:
1500 + (1500 * 20/100%) = 1800 (м).
Находим весь пройденный путь за 2 дня:
1500 + 1800 = 3300 (м).
Находим какую часть составляет пройденный путь от запланированного:
3300 /5000 = О,66 или 66%.
Ответ: О,66 часть или 66% маршрута пройдено альпинистом от запланированного.
![]()
AlexSEO
[85.9K]
4 года назад
Если в первый день было преодолено альпинистом 30%, то во второй день: 30% + 30% * 0,2 = 36%. Всего получается 66% или (в метрах) 3300, что и будет ответом на задачу. Остаток пути составляет: в процентах — 34, а в метрах — 5000 * 0,34 = 1700 метров.
Знаете ответ?
Введите переменную
Примем длину всего маршрута туриста за неизвестную переменную х.
Выразите длину маршрута, пройденного в первый день, через переменную х
Выразим длину пройденного пути за первый и второй дни с использованием введенной переменной.
Известно, что в первый день турист прошел половину всего маршрута. То есть длина маршрута, пройденного в первый день, составила 1/2 * х, или 0,5 * х, если указывать расстояние в десятичных дробях.
Выразите длину маршрута, пройденного во второй день, через переменную х
Длина пути, пройденного во второй день, равна 2/3 оставшейся части.
Так как известно, что в первый день турист прошел половину всего маршрута, то оставшаяся часть составит так же половину пути, то есть 1/2 * х.
Тогда длина пройденного во второй день пути равна 2/3 * 1/2 * х.
Выполним пошаговое преобразование:
- Умножим значения в числителях дробей, то есть 2 * 1 * х. Получим 2 * х.
- Умножим значения в знаменателях дробей, то есть 3 * 2. Получим 6.
- Запишем получившееся значение: 2х / 6, или 2/6 * х. Видно, что и числитель, и знаменатель дроби делятся на число 2. Разделив, получим значение 1/3 * х.
Найдите длину маршрута, пройденного в третий день, через длины маршрутов, пройденных в первый и второй дни
Известно, что в первый день турист прошел 1/2 * х, во второй — 1/3 * х. Тогда для того чтобы найти длину пути, пройденного в третий день, необходимо из общей длины маршрута (х) вычесть длины маршрутов, пройденных в первый и второй дни: х — 1/2 * х — 1/3 * х.
Для упрощения вынесем х за скобки, запишем х * (1 — 1/2 — 1/3).
Далее приведем значения в скобках к общему знаменателю. В данном случае общим знаменателем является число 6х, которое без остатка делится на 1, 2 и 3.
Запишем х * (6 — 3 — 2) / 6. После вычитания в скобках получаем число 1. Получаем, что в третий день турист прошел расстояние 1/6 * х.
Проверка
Сложив длины маршрутов, пройденных туристом за 3 дня, получим:
1/2 * х + 1/3 * х + 1/6 * х = (3+2+1) / 6 * х = х, что равно общей длине пройденного пути.
Как найти часть пути
Как найти часть путиСкачать файл — Как найти часть пути
Чтобы решить задачу с дробями, нужно научиться делать с ними арифметические действия. Они могут быть десятичные, но чаще всего используются натуральные дроби с числителем и знаменателем. Только после этого можно переходить на решения математических задач с дробными величинами. Дробью называют запись деления одного числа на другое. Зачастую это сделать нацело нельзя, поэтому и оставляют это действие неоконченным. Число, которое является делимым оно стоит над или перед знаком дроби , называются числителем, а второе число под знаком дроби или после него знаменателем. Если числитель больше знаменателя, дробь называется неправильной, и из нее можно выделить целую часть. Если числитель меньше знаменателя, то такая дробь называется правильной, и ее целая часть равна 0. Задачи с дробями делятся на несколько видов. Определите, к какому из них относится задача. Простейший вариант нахождение доли числа, выраженной дробью. Для решения этой задачи достаточно умножить это число на дробь. Например, на склад завезли 8 т картошки. Если нужно найти число по его части, умножьте известную часть числа на дробь, обратную той, которая показывает какова доля данной части в числе. Сколько детей учится в классе? Когда нужно найти какую часть числа составляет одно число от другого, поделите число, которое представляет часть на то, которое является целым. К примеру, если расстояние между городами км, а автомобиль проехал км, какую часть этот составит от всего пути? Поделите часть пути на полный путь , после сокращения дроби получите результат. Чтобы найти часть неизвестную долю от числа, когда есть известная, возьмите целое число за условную единицу, и отнимите от нее известную долю. ВЫЧИТАНИЕ При сложении вычитании дробей с разными знаменателямипредварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным. УМНОЖЕНИЕ При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель произведению знаменателей. Числитель умножаешь на числитель, знаменатель-соответственно. Сама часто путаюсь тут Для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую. А со смешанными числами многое не изменяется При делении или умножении сначала нужно преобразовать смеш. Знаменатель умножить на целую часть 2. К этому прибавить числитель 3. Сумма этого- это ЧИСЛИТЕЛЬ 4. При сложении или вычитании совсем необязательно это делать Но можно И еще, меня всегда ругали за то, что забывала сократить дробь! Чтобы сократить дробь, надо и числитель, и знаменатель разделить на их нод общий делитель Если это возможно. Пожалуйста, объсните как сокращать дроби. Как из обычой дроби сделать десятичную? Как разделить целое число на дробь? Posted in Архитектура и строительство Навигация по записям как на iPhone? От RGS-Life Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован. Как решать дроби подскажите просто болею и не чего не понимаю. Как решать дроби подскажите просто болею и не чего не понимаю Posted on Инструкция 1 Дробью называют запись деления одного числа на другое. СЛОЖЕНИЕ При сложении вычитании дробей с одинаковыми знаменателямиполучается дробь с тем же знаменателем, а е числитель равен сумме разности числителей рассматриваемых дробей. Числитель умножаешь на числитель, знаменатель-соответственно ДЕЛЕНИЕ! Знаменатель остается прежним При сложении или вычитании совсем необязательно это делать Но можно И еще, меня всегда ругали за то, что забывала сократить дробь! Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован.
Решение задач по теме ‘Нахождение части от числа и числа по его части’
Вид коробки вариатор
Ткемали из крыжовника без варки
Как решать! Как решать дроби подскажите просто болею и не чего не понимаю
Rss для спортивных новостей себе на сайт
Инструкции по охране труда в офисе образец
Миноискатель сколько стоят
Описание и характеристики свечей на 406 двс
Как найти среднюю скорость
Милавица в могилеве каталог
Сословно представительская монархия
Like reading перевод
Нахождение числа по его дроби
Скачать клипы с ютуба без регистрации
Леруа пушкино карта
Приказ об утверждении свидетельства об обучении
На уроке математики, на улице, в магазине, в быту и профессиональной деятельности, науке и технике часто приходится встречаться с дробями и решать различные задачи с ними.
Эта информация доступна зарегистрированным пользователям
Так, например, в кулинарии очень часто используют дробные числа, отмеряя те или иные ингредиенты в соответствии с рецептом: пол чайной ложки соли, треть стакана, четверть пачки, полкилограмма сахара и т.д.
Определяя время по часам, приходится находить часть от часа, от минуты, например, 30 минут равняется ½ часа, четверть часа (15 минут)- это ¼ часа, 30 секунд равняются ½ минуты, 15 секунд составляют ¼ минуты.
Эта информация доступна зарегистрированным пользователям
В медицине и фармацевтике используют дробные числа.
В состав лекарственного средства чаще всего включают дробное количество различных действующих и вспомогательных веществ.
Эта информация доступна зарегистрированным пользователям
Для корректного лечения врач устанавливает эффективную дозировку лекарственного препарата, которая иногда представлена в виде дробного числа.
Дозировку или концентрацию лекарственного средства приходится выражать в виде дроби: полтаблетки (1/2), четверть (1/4) таблетки и т.д.
Особенно важно учитывать количество медицинского препарата для пациентов детского возраста.
Часто дозировку лекарства для детей рассчитывают относительно взрослой дозы на основе данных о массе ребенка, количестве лет и др.
Обыкновенные дроби широко используются в строительстве и архитектуре.
Создавая надежную конструкцию, важно соблюдать соизмеримость и определенные соотношения частей сооружения.
Эта информация доступна зарегистрированным пользователям
Начертить чертеж, построить здание, возвести мост, положить асфальт, приготовить бетонную смесь невозможно без знаний о дробях.
В спортивных состязаниях вам, наверное, не раз приходилось слышать такие фразы: «состоялся четверть финал» или «полуфинал чемпионата», «одна восьмая финала».
Дроби используют в искусстве, например, в музыке, живописи и др.
Одним из примеров внедрения дробей в музыкальное искусство может служить нотная грамота.
Еще древнегреческий ученый Пифагор установил связь между длительностью музыкального звучания и дробей.
Дроби применяют для обозначения длительности нот.
Так, например, существует длинная нота.
Кроме нее есть половинная нота, четвертная, восьмая, шестнадцатая и т.д.
Эта информация доступна зарегистрированным пользователям
Такое обозначение нот удобно, так как явно видно насколько одна нота длиннее или короче другой.
Существует еще одна важная роль дробного числа в музыке.
Музыкальный размер (количество ритмических единиц в такте) так же обозначают в виде дроби (только без дробной черты) вначале нотной строки.
Эта информация доступна зарегистрированным пользователям
С помощью музыкального размера музыканты понимают с каким ритмом и темпом нужно играть музыкальное произведение.
В картографии и географии с помощью дроби указывают масштаб карты.
Деление целого на доли встречается в юридической практике при делении наследства.
В повседневной жизни мы часто делим целое на части, например, плитку шоколада ломаем на дольки, чтобы угостить друзей, режем на кусочки торт на празднике, делим мандарин на дольки и т.д.
Мы можем привести бесконечное множество примеров деления чего-либо на части.
Сегодня на уроке вспомним, что называют долей числа и, что представляет собой дробь от числа.
Эта информация доступна зарегистрированным пользователям
Научимся решать задачи, в которых необходимо находить часть от целого и целое по его части.
Рассмотрим алгоритм и примеры решения таких задач.
В математике дробью обозначают часть некоторой рассматриваемой величины, часть от целого.
Каждую равную часть одного целого называют долей числа.
Дробь представляет собой число, которое состоит из одной или нескольких долей (равных частей) целого.
Математическая запись обыкновенной дроби оформляется в виде двух чисел, разделенных чертой, которая называется дробной (она может быть горизонтальной и наклонной).
Число, стоящее над дробной чертой, называют числителем.
Числитель показывает, сколько долей взяли от целого.
Число, стоящее под дробной чертой, называют знаменателем.
Знаменатель показывает, на сколько всего равных долей разделили целое.
Зная целое, можно найти его часть.
Рассмотрим такую задачу.
Эта информация доступна зарегистрированным пользователям
Ленту, длиной 12 дм, разрезали на 2 равные части.
Что значит разрезать на две равные части?
Это значит, что ленту нужно разделить на две доли, каждая из которых является половиной этой ленты.
Эта информация доступна зарегистрированным пользователям
Итак, каждая доля- это половина всей ленты, по-другому такую часть от целого называют одна вторая часть ленты, обозначают ½.
В нашем примере половина всей ленты, т.е. одна вторая часть ее составляет 6 дм.
Запишем равенство: 12 ÷ 2 = 6 (дм).
Ленту такой же длины разделим на четыре равные части.
Эта информация доступна зарегистрированным пользователям
Получим 4 доли, каждая из которых равна одной четвертой всей длины ленты, обозначается 1/4.
Четверть (одна четвертая) ленты составляет: 12 ÷ 4 = 3 (дм).
Попробуем найти одну шестую ленты все той же длины- 12 дм.
Эта информация доступна зарегистрированным пользователям
1/6 доля этой ленты будет составлять: 12 ÷ 6 = 2 (дм).
Итак, нам становится ясно, чтобы найти долю от числа, необходимо разделить это число на количество долей (равных частей).
Рассмотрим ситуацию посложней.
Полоску бумаги, длиной 15 см, разделим на 5 равных частей (пять долей).
Эта информация доступна зарегистрированным пользователям
Определим, чему будет равны (mathbf{frac{3}{5}}) этой полоски бумаги.
Одна доля ((mathbf{frac{1}{5}}) этой полоски)- это 15 ÷ 5 = 3 (см).
Возьмем три таких доли.
Так как одна доля составляет 3 см, то три доли будут равны 3 ∙ 3 = 9 (см).
В данном случае получилось, что три пятых полоски бумаги составляют 9 см.
Сформулируем правило нахождения части от целого.
Чтобы найти несколько долей целого (дробь от числа), необходимо найти величину одной доли, затем умножить ее на количество долей.
Запишем алгоритм нахождения части от числа (несколько долей целого).
1. Найти величину одной доли.
2. Величину одной доли умножить на количество взятых долей.
В буквенном виде данное правило можно представить так:
Пусть А— это исходное число.
В— неизвестная часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m— числитель, показывает сколько долей взяли.
n— знаменатель, показывает на сколько долей разделили число А.
Чтобы найти часть числа А, необходимо это число А разделить на знаменатель (n) и умножить на числитель (m) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
В качестве примера рассмотрим решение нескольких задач.
Задача №1.
Туристы за все время своего путешествия из пункта А в пункт В должны пройти 54 км.
Туристы прошли (mathbf{frac{1}{2}}) всего пути по лесу.
Сколько километров прошли туристы по лесу? Сколько им осталось пройти?
Решение:
Вспомним правило.
Чтобы найти долю от числа, необходимо число разделить на количество долей.
Прошли (mathbf{frac{1}{2}}) всего пути- это значит туристы преодолели половину своего пути.
Разделим весь путь на 2 равные доли, т.е. на 2, в результате получим (mathbf{frac{1}{2}}) пути, которую туристы прошли по лесу.
Этот путь будет составлять: 54 ÷ 2 = 27 (км).
Определим путь, который им осталось пройти, для этого из общего пути вычтем пройденный по лесу путь:
54 — 27 = 27 (км) туристам осталось пройти.
Ответ: 27 (км), 27 (км).
Задача №2
За три дня туристы прошли 54 километра.
За первый день они прошли половину всего пути.
За второй день преодолели (mathbf{frac{2}{3}}) оставшегося пути.
Сколько километров туристы прошли в каждый из трех дней?
Решение:
Весь трехдневный путь туристов составляет 54 км.
Первый день туристы прошли половину- это (mathbf{frac{1}{2}}) всего пути.
Выше в задаче №1 мы уже находили (mathbf{frac{1}{2}}) от 54 (км), у нас получился следующий результат:
54 ÷ 2 = 27 (км) прошли туристы в первый день.
Так как в первый день пройдена половина пути, то вторая половина- это оставшийся путь.
Он будет равен: 54 — 27 = 27 (км).
Второй день- это (mathbf{frac{2}{3}}) оставшегося пути, т.е. (mathbf{frac{2}{3}}) от 27 (км).
Чтобы найти дробь от числа, необходимо найти величину одной доли, затем умножить ее на количество частей (долей).
Найдем величину одной доли, для этого весь оставшийся путь (27 км) разделим на знаменатель дроби (в нашем случае это число 3), данное выражение будет описываться выражением 27 ÷ 3.
Полученный результат умножим на количество, пройденных туристами долей, на которые нам указывает числитель дроби (он равен 2).
В результате получим равенство:
27 ÷ 3 ∙ 2 = 9 ∙ 2 = 18 (км) туристы прошли во второй день.
Так как во второй день туристы прошли 18 км от пути, оставшегося после первого туристического дня (т.е. 18 км из 27 км), то за третий день им осталось пройти:
27 — 18 = 9 (км) туристы прошли в третий день.
Проверим полученные результаты.
Найдем весь туристический путь за три дня, он должен быть равен 54 км.
Для этого сложим путь первого, второго и третьего дня.
27 + 18 + 9 = 45 + 9 = 54 (км) прошли туристы за три дня.
Задача решена верно.
Ответ: 27 (км), 18 (км), 9 (км).
Эта информация доступна зарегистрированным пользователям
Если известно сколько составляет часть от целого, то по известной части можно найти целое.
Рассмотрим задачу:
Пусть длина (mathbf{frac{1}{2}}) ленты составляет 10 дм.
Определим, чему равна длина всей ленты.
Эта информация доступна зарегистрированным пользователям
Так как (mathbf{frac{1}{2}}) ленты- это ее половина, и она составляет 10 дм, то вторая половина так же равна 10 дм.
В таком случае, чтобы найти длину всей ленты, мы можем сложить длины этих двух половинок или, заменив сложение одинаковых слагаемых умножением, можем по 10 дм взять два раза, в результате получим равенство:
10 ∙ 2 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрим еще одну задачу, в которой будет известна длина одной четвертой части ленты.
Ленту подарочную разделили на четыре части.
Длина (mathbf{frac{1}{4}}) ленты составляет 5 дм.
Эта информация доступна зарегистрированным пользователям
Определим, чему равна длина всей ленты.
Целое, т.е. всю ленту разделили на 4 доли.
Известно, что одна доля- это (mathbf{frac{1}{4}}) ленты, она составляет 5 дм.
Чтобы найти длину всей ленты, необходимо длину одной доли (в нашем случае 5 дм) умножить на количество долей (в нашем примере их 4).
Получим следующее равенство:
5 ∙ 4 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Рассмотрев эти два примера, можно сделать вывод:
Чтобы найти неизвестное число по его доле, необходимо долю этого числа умножить на число долей.
Усложним задачу про ленту и попробуем ее решить.
Пусть подарочную ленту разделили на 5 равных частей.
Определим, какова длина всей ленты, если (mathbf{frac{3}{5}}) этой ленты составляет 12 дм.
Эта информация доступна зарегистрированным пользователям
Из условия задачи известно, что разделили ленту на 5 долей, а 3 таких доли составляют 12 дм.
Для того чтобы найти длину всей ленты, необходимо найти длину одной доли.
Следовательно, известную длину трех долей (12 дм) разделим на количество этих долей (3 доли).
Данное действие будет описывать следующее выражение: 12 ÷ 3.
Затем умножим длину одной доли на количество всех долей (в нашем случае всю ленту разделили на 5 долей).
В результате получим равенство:
12 ÷ 3 ∙ 5 = 4 ∙ 5 = 20 (дм) длина всей ленты.
Ответ: 20 (дм).
Сформулируем правило нахождения целого по его части.
Чтобы найти целое по его части, необходимо определить величину одной доли, затем полученный результат умножить на общее количество долей (на которое поделено целое).
Запишем алгоритм нахождения числа по его дроби.
1. Найти величину одной доли.
2. Величину одной доли умножить на количество всех долей, на которое разделено число.
В буквенном виде данное правило можно представить так:
Пусть А— это исходное число, оно неизвестно.
В— часть числа А, выраженная дробью (mathbf{frac{m}{n}}).
m— числитель, показывает сколько долей взяли.
n— знаменатель, показывает на сколько долей разделили число.
Чтобы найти исходное число А, необходимо число В, соответствующее части числа А, разделить на числитель (m) и полученный результат умножить на знаменатель (n) дроби, которая выражает эту часть.
Эта информация доступна зарегистрированным пользователям
Рассмотрим, как данное правило применяется при решении задач.
Задача №1.
Дима потратил на сладости 120 рублей, что составляет (mathbf{frac{2}{4}}) всех накопленных им денег.
Сколько всего денег было у Димы накоплено?
Решение:
Общее количество денег, которое было у Димы не известно.
Известно только то, что 120 рублей- это часть всех денег Димы.
Эта же часть денег выражена дробью (mathbf{frac{2}{4}}) от всех денег.
Знаменатель данной дроби показывает на то, что все накопленные деньги разделены на 4 части, а числитель дроби указывает на то, что две части из четырех составляют 120 рублей.
Найдем величину одной доли (одной части из четырех), т.е. сколько составляет (mathbf{frac{1}{4}}) (четверть) всех денег Димы.
120 ÷ 2 = 60 (руб.) составляет четверть всех денег Димы.
Чтобы найти общее количество денег, которые накопил Дима (а это четыре части по 60 рублей), нужно:
4 ∙ 60 = 240 (руб.) было накоплено у Димы.
Кратко решение данной задачи можно записать следующим образом:
120 ÷ 2 ∙ 4 = 240 (руб.) было накоплено у Димы.
Ответ: 240 (руб.)
Очень часто задачи такого типа имеют более сложные условия и их приходится решать в несколько действий.
Задача №2.
Дима купил шоколадку. Он за нее заплатил 60 рублей, что составило (mathbf{frac{1}{3}}) всех его денег.
От оставшейся суммы (mathbf{frac{2}{3}}) он потратил на мороженное, остальные деньги положил в копилку.
Сколько денег Дима положил в копилку?
Решение:
Первым делом определим первоначальную сумму, которая была у Димы.
Будем считать, что искомое число состоит из трех долей.
По условию задачи одна доля составляет 60 рублей.
Чтобы найти число (целое) по его доле, необходимо долю этого числа умножить на число долей.
В таком случае получаем:
60 ∙ 3 = 180 (руб.) всего было накоплено у Димы- это первоначальная сумма, которая у него была.
Следующим действием найдем часть денег, которые потратил Дима на мороженное.
Из общей суммы денег вычтем 60 рублей, которые были потрачены на шоколадку.
180 — 60 = 120 (руб.) оставшееся сумма денег у Димы.
От полученного остатка найдем (mathbf{frac{2}{3}})
Чтобы найти (mathbf{frac{2}{3}}) от 120 (дробь от числа), нужно число 120 разделить на знаменатель и умножить на числитель этой дроби.
120 ÷ 3 ∙ 2 = 40 ∙ 2 = 80 (руб.) Дима потратил на мороженное.
Из первоначальной суммы (180 рублей) вычтем деньги, потраченные на шоколадку, (60 рублей), вычтем деньги, потраченные на мороженное, (80 рублей) и получим остаток денег, который Дима положил в копилку.
180 — 60 — 80 = 100 — 60 = 40 (руб.) Дима положил в копилку.
Ответ: 40 (руб.)
Эта информация доступна зарегистрированным пользователям
Читайте также
Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой “+”.
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути – со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
Светило науки – 3 ответа – 0 раз оказано помощи
Нам известно, что в третий день ледокол прошёл 90 км. Неизвестно, какая эта доля пути. Следовательно, находим долю пути, которую прошёл ледокол в третий день. Остав¬шийся путь принимаем за целое, которую представим в виде дроби: , вычтем из него долю пути, которую прошёл ледо¬кол за второй день: .
По формуле нахождения числа по его доле находим, ка¬кой путь прошёл ледокол за второй и третий день: 90 : 3 • 8 = 240 км.
Теперь примем за целое весь путь и найдём, какую долю пути осталось пройти ледоколу за второй и третий день:
.
По формуле нахождения числа по его доле находим весь путь, который прошёл ледокол за три дня: 240 : 3 • 5 = 400 км.
По формуле нахождения части числа находим, какой путь прошёл ледокол за первый и второй день:
400 : 5 • 2 = 160 км – в первый день;
240 : 8 • 5 = 150 км – во второй день.
Ответ. В первый день ледокол прошёл 160 км, во второй день – 150 км; за три дня – 400 км.
