Как найти domain and range

Functions in mathematics can be compared to the operations of a vending (soda) machine. When you put in a certain amount of money, you can select different types of sodas. Similarly, for functions, we input different numbers and we get new numbers as the result. Domain and range are the main aspects of functions.

• You can use quarters and one-dollar bills to buy a soda. The machine will not give you any flavor of the soda if pennies are input. Hence, the domain represents the inputs we can have here, that is, quarters and one-dollar bills.
• No matter what amount you pay, you won’t get a cheeseburger from a soda machine. Thus, the range is the possible outputs we can have here, that is, the flavors of soda in the machine.

Let us learn to find the domain and range of a function, and also graph them.

1.	What is Domain and Range?
2.	Domain and Range of a Function
3.	Domain of a Function
4.	Range of a Function
5.	How To Calculate Domain And Range?
6.	Domain and Range of Exponential Functions
7.	Domain and Range of Trigonometric Functions
8.	Domain and Range of an Absolute Value Function
9.	Domain and Range of a Square Root Function
10.	Domain and Range From Graph
11.	FAQs on Domain and Range

What is Domain and Range?

The domain and range of a relation are the sets of all the x-coordinates and all the y-coordinates of ordered pairs respectively. For example, if the relation is, R = {(1, 2), (2, 2), (3, 3), (4, 3)}, then:

• Domain = the set of all x-coordinates = {1, 2, 3, 4}
• Range = the set of all y-coordinates = {2, 3}

We can visualize this here:

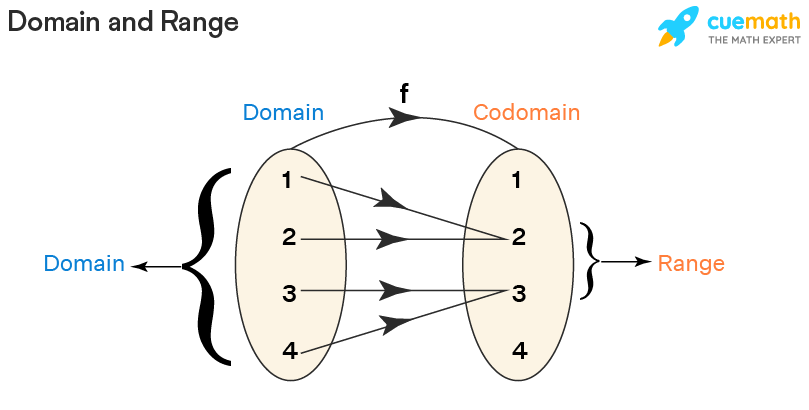
The concept of domain and range is further implemented for functions as well.

Domain and Range of a Function

The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and the range is the possible output given by the function. Domain→ Function →Range. If there exists a function f: A →B such that every element of set A is mapped to elements in set B, then A is the domain and B is the co-domain. The image of an element ‘a’ under a relation R is given by ‘b’, where (a,b) ∈ R. The range of the function is the set of images. The domain and range of a function are denoted in general as follows: Domain(f) = {x ∈ R : Condition} and range(f)={f(x) : x ∈ domain(f)}

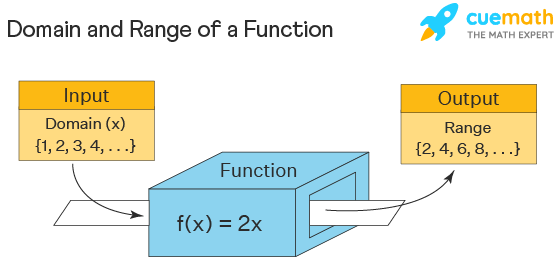
The domain and range of this function f(x) = 2x is given as domain D = {x ∈ N} , range R = {y ∈ N: y = 2x}

Domain of a Function

A domain of a function refers to “all the values” that can go into a function without resulting in undefined values. i.e., The domain in math is the set of all possible inputs for the function. Consider the above box as a function f(x) = 2x . Inputting the values x = {1,2,3,4,…}, the domain is simply the set of natural numbers. But in general (if the domain is not specified as natural numbers), f(x) = 2x is defined for all real values of x and hence its domain is the set of all real numbers which is denoted by (-∞, ∞). Here are the general formulas used to find the domain of different types of functions. Here, R is the set of all real numbers.

Rules of Finding Domain of a Function

1. Domain of any polynomial (linear, quadratic, cubic, etc) function is ℝ (all real numbers).
2. Domain of a square root function √x is x ≥ 0.
3. Domain of an exponential function is ℝ.
4. Domain of logarithmic function is x>0.
5. To find the domain of a rational function y = f(x), set the denominator ≠ 0.

How to Find Domain of a Function?

To find the domain of a function, we simply apply one of the above-mentioned rules of finding domain depending on the type of the function. Here are some examples:

Example 1: To find the domain of a function f(x) = √(x + 3), we apply the rule 2 mentioned above. Then we get: x + 2 ≥ 0. Solving this inequality, we get x ≥ -2. Thus, the domain of f(x) is [-2, ∞).

Example 2: To calculate the domain of a function g(x) = (2x + 1) / (x – 2), we apply the rule 5 mentioned above. Then we get x – 2 ≠ 0. Solving this, we get x ≠ 2. Thus, its domain is the set of all real numbers except 2 which in interval notation can be written as (-∞, 2) ∪ (2, ∞).

Range of a Function

The range of a function is the set of all its outputs. Example: Let us consider the function f: A→ B, where f(x) = 2x and each of A and B = {set of natural numbers}. Here we say A is the domain and B is the co-domain. Then the output of this function becomes the range. The range = {set of even natural numbers}. The elements of the domain are called pre-images and the elements of the co-domain which are mapped are called the images. Here, the range of the function f is the set of all images of the elements of the domain (or) the set of all the outputs of the function.

Rules of Finding Range of a Function

The best way to determine the range of a function is by graphing it and looking at the y-value that the graph covers. But here are the general rules used to find the range of some popular functions. Note that ℝ is the set of all real numbers here.

1. Range of a linear function is ℝ.
2. Range of a quadratic function y = a(x – h)² + k is:
   y ≥ k, if a > 0 and
   y ≤ k, if a < 0
3. Range of a square root function is y ≥ 0.
4. Range of an exponential function is y > 0.
5. Range of logarithmic function is ℝ.
6. To find the range of a rational function y = f(x), solve it for x and set the denominator ≠ 0.

How to Find Range of a Function?

If a function is present in one of the functions mentioned in the above rules, we can straight away apply the rules and find its range. Otherwise, we can graph it and look at the y-values the graph covers to calculate range. Here are some examples:

Example 1: To calculate the range of the function f(x) = 2 (x – 3)² – 5, apply rule 1 mentioned above. Then its range is y ≥ -5 (or) [-5, ∞).

Example 2: To find the range of a function g(x) = ln (2x – 3) + 4, we apply the rule 4. Then we get its range to be the set of all real numbers (ℝ).

How To Calculate Domain And Range?

Suppose X = {1, 2, 3, 4, 5} and Y = {1, 2, 3, 4, 5, 6}. Consider the function f: X → Y, where R = {(x,y) : y = x+1}.

• Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
• Range = the output values of the function = {1 + 1, 2 + 1, 3 + 1, 4 + 1, 5 + 1} = {2, 3, 4, 5, 6}

Note that Y is the codomain here but NOT range.

Let’s understand the domain and range of some special functions taking different types of functions into consideration.

Domain and Range of Exponential Functions

The function y = a^x, a ≥ 0 is defined for all real numbers. Hence, the domain of the exponential function is the entire real line. The exponential function always results in a positive value. Thus, the range of the exponential function is of the form y= a^x is {y ∈ ℝ: y > 0}. Therefore, Domain = ℝ, Range = (0, ∞)

Example: Look at the graph of this function f: 2^x

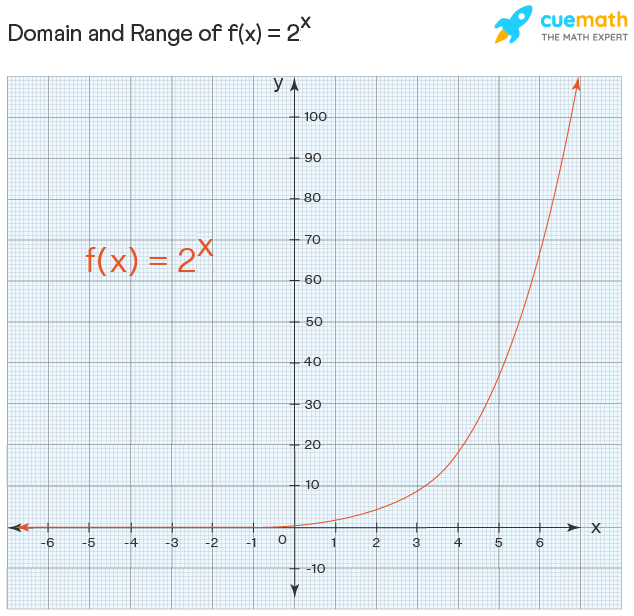
Observe that the value of the function is closer to 0 as x tends to ∞ but it will never attain the value 0. The domain and range of exponential functions are given as follows:

• Domain: The domain of the function is the set ℝ.
• Range: The exponential function always results in positive real values.

Domain and Range of Trigonometric Functions

Look at the graph of the sine function and cosine function. Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.

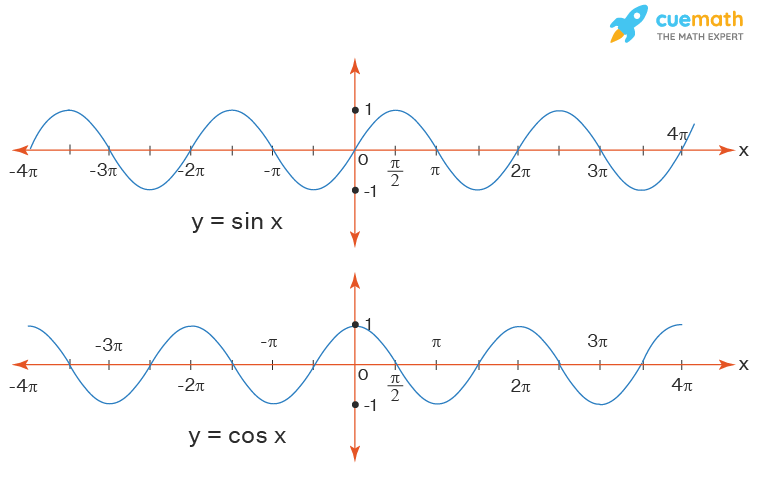
Thus, for each of the sine and cosine functions:

• Domain: The domain of the functions is the set ℝ (or) (-∞, + ∞).
• Range: The range of the functions is [-1, 1]

The domain and range of all trigonometric functions are shown below:

Trigonometric Functions	Domain	Range
sin θ	(-∞, + ∞)	[-1, +1]
cos θ	(-∞ +∞)	[-1, +1]
tan θ	ℝ – (2n + 1)π/2	(-∞, +∞)
cot θ	ℝ – nπ	(-∞, +∞)
sec θ	ℝ – (2n + 1)π/2	(-∞, -1] U [+1, +∞)
cosec θ	ℝ – nπ	(-∞, -1] U [+1, +∞)

Domain and Range of an Absolute Value Function

The function y = |ax + b| is defined for all real numbers. So, the domain of the absolute value function is the set of all real numbers. The absolute value of a number always results in a non-negative value. Thus, the range of an absolute value function of the form y= |ax+b| is {y ∈ ℝ | y ≥ 0}. The domain and range of an absolute value function are given as follows

• Domain = ℝ
• Range = [0, ∞)

Example: Find the domain and range of the function f(x) = |6 – x|.

• Domain: The domain of the function is the set ℝ.
• Range: Its range is [0, ∞)

Domain and Range of a Square Root Function

A square root function is of the form f(x) = √(ax+b). We know that the square root of a negative number is not defined. So the function y= √(ax+b) is defined only when ax + b ≥ 0. When we solve this for x, we get x ≥ -b/a.

So, the domain of the square root function is the set of all real numbers greater than or equal to -b/a. We know that the square root of something always results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. Hence, the domain and range of a square root function are given as: Domain = [-b/a,∞), Range = [0,∞)

Example: Calculate the domain and range of the function h(x) = 2- √(-3x+2).

Domain: A square root function is defined only when the value inside it is a non-negative number. So for a domain,

-3x+2 ≥ 0

-3x ≥ -2

x ≤ 2/3

Range: We already know that the square root function results in a non-negative value always.

√(-3x+2) ≥ 0

Multiply -1 on both sides

-√(-3x+2) ≤ 0

Adding 2 on both sides

2-√(-3x+2) ≤ 2

y≤ 2

Thus, the domain of h(x) = (-∞, 2/3] and range of h(x) = (-∞, 2].

Domain and Range From Graph

It is very easy to find the domain and range of a graph. The set of values of x covered by the graph gives the domain and the set of values of y covered by the graph gives the range. But keep a note of the following things while writing the domain and range from a graph.

• See whether the graph passes the vertical line test. Otherwise, it is not a function and we do not usually define domain and range for such curves.
• If there is any hole on the graph, then its coordinates shouldn’t be in the domain and range.
• If there is a vertical asymptote, then the corresponding value of x shouldn’t be there in the domain.
• If there is a horizontal asymptote, then the corresponding value of x shouldn’t be there in the range.
• If the graph is broken into pieces, then we get multiple sets/intervals in the domain and range and we club all such sets/intervals by “union” symbol (∪).
• If there is an arrow at the end of a curve, then it means that the curve is supposed to be extended infinitely in that particular direction.

Example 1:

Here is an example of a graph and we will find the domain and range of the graph.

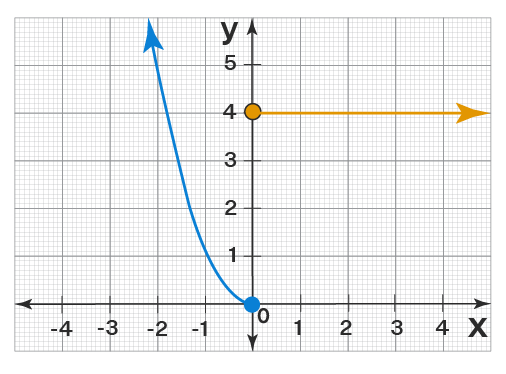
In the above graph:

• All the x-values from -∞ to ∞ are covered by the graph (because of arrows, the two curves extend infinitely in the given directions). Hence, the domain = (-∞, ∞).
• All the y-values greater than or equal than or equal to 0 are covered by the graph (see there is no part of the curve that is below the y-axis). Hence, the range = [0, ∞).

Example 2: Using the same process mentioned above, the domain of the graph below is [-5, ∞) and its range from graph is (-∞, 5].

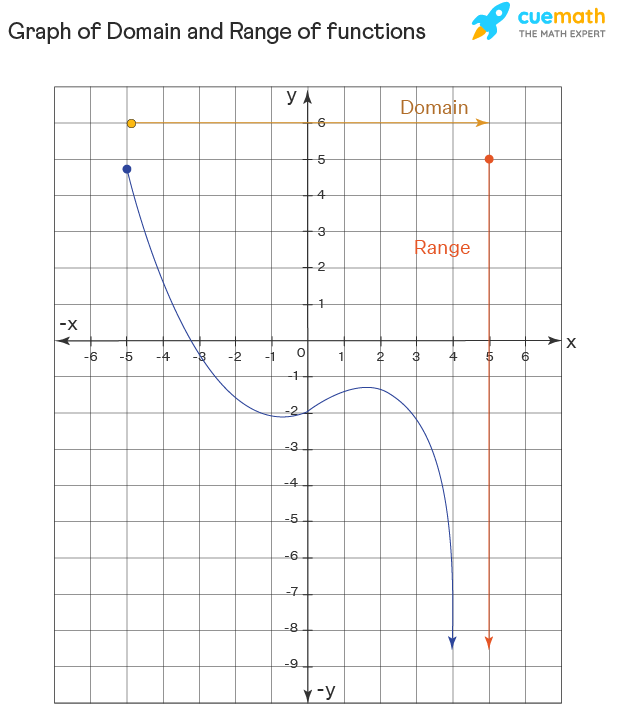
Important Notes on Domain and Range:

• The domain and range of a function is the set of all possible inputs and outputs of a function respectively.
• To find the domain of a function f(x), think for what values of x it is defined.
• To calculate the range of a function f(x), think of what y values it will produce. The most easiest way to find the range of a function is to graph it.

☛ Related Topics:

• Graphing Functions
• Cubic Functions
• Inverse Trigonometric Functions

FAQs on Domain and Range

What is the Domain and Range of a Function?

The domain and range of a function are the set of all the inputs and outputs a function can give respectively. i.e., for any function y = f(x):

• the domain is the set of all x-values for which f(x) is defined.
• the range is the set of all y-values that the function f(x) produce.

How Do You Write the Domain and Range?

We write the domain and range of a function as the set of all the inputs a function can take and the outputs of the functions respectively. Since these are nothing but sets, we can write them either in roaster form or set builder notation. The domain and range in the interval notation involve open and square brackets.

How to Find Domain and Range of a Graph?

The domain from a graph is the set of all x-values the graph covers and the range of a graph is the set of all y-values that it covers.

What is The Domain and Range of a Constant Function?

Let the constant function be f(x) = k. The domain of a constant function is given by ℝ, that is, the set of real numbers. The range of a constant function is given by the singleton set, {k}. The domain and range of a constant function is given as domain = ℝ and range = {k}, which is a singleton set.

What is the Definition of Domain in Math?

The domain in math is usually defined for relations/functions. The domain of a function is the set of all values that are possible to input into it. For example, for the function f(x) = √x, it is possible to input only non-negative values into it. Thus, its domain is the set of all non-negative real numbers.

How to Find the Domain of a Function which is Rational?

To find the domain of a rational function, we just set the denominator not equal to zero. For example, to find the domain of f(x) = 2/(x-3), we set x-3 ≠ 0, by solving this, we get x≠3. So the domain is the set of all rational numbers except 3. This can be written in the interval notation as (-∞, 3) U (3, ∞).

What are the Rules to Find the Domain of a Function?

Here are some general rules used to find domain of different types of functions:

• f(x) = polynomial, the domain is the set of all real numbers.
• f(x) = 1/x, domain if the set of all real numbers but x≠0.
• f(x) = √x, domain if the set of all real numbers such that x ≥ 0.
• f(x) = ln x, domain is the set of all real numbers such that x > 0.

How to Find Domain and Range of Function?

To find the domain of a function y = f(x), we need to look for set of all possible values of x that does not make the function undefined. The common examples include dividing by 0, taking the square root of negative numbers, etc. To calculate the range of a function, imagine what y-values the function produces. When imagination is not possible, graph the function and take a look at the y-values that the graph covers.

How to Find Range of a Rational Function?

To find the range of a rational function, we just solve the equation for x and set the denominator not equal to zero. For example, to find the range of y=2/(x-3), solve it for x first. Then we get, x-3 = 2/y and from this, x = (2/y) + 3. Then its range is y≠0 (or) in interval notation, (-∞, 0) U (0, ∞).

How to Find Domain and Range of an Equation?

To find the domain and range of an equation y = f(x), determine the values of the independent variable x for which the function is defined. To calculate the range of the function, we simply express the equation as x = g(y) and then find the domain of g(y).

How to Calculate the Domain and Range From the Graph of a Function?

The set of all x-coordinates of all points of the curve would give the domain and the set of all y-coordinates of all points of the curve would give the range. Each of domain and range can be either written as a set or an interval.

What is The Difference Between Domain and Range of a Function?

Domain and Range of a function are the components of a function. The domain of a function is the set of all possible inputs for the function, whereas the range of function is the set of all the outputs a function can give.

What is The Domain and Range of a Relation?

The domain and range of a relation is found as follows. Let R be the relation from a non-empty set A to a non-empty set B. The domain and range of the relation are the set of first elements and the second elements respectively in the ordered pairs in relation R is called the domain.

What is the Domain and Range of Composite Functions?

Let the composite function be h(x) = (f ∘ g)(x). The domain and range of h are determined as follows. The domain of h is either same as f or lies within the domain of f. The range h must lie within the range of g. Let f(x) = x² and g(x) = x+ 3. We know that g: X →Y and f: Y →Z. Then fog: X →Z. f(g(x)) = (x+3)². Thus the domain and range are: domain= {All the elements in set X}, range= {all the elements in set Z}

What is the Domain and Range of a Quadratic Function?

The domain and range of a quadratic function y = a(x – h)² + k determine the nature of the parabola: whether it is upwards or downwards.

• y ≥ k, if the function has a minimum value, that is, when a > 0 (parabola opens up)
• y ≤ k, if the function has a maximum value, that is, when a < 0 (parabola opens down)

How to Find the Range of a Graph?

The y-axis is responsible for range. Thus, to find the range of a graph look at the y-values covered by the graph. The highest and lowest values of the graphs are helpful in writing the range of a graph.

A function is defined as the relation between a set of inputs and their outputs, where the input can have only one output. It depicts a relationship between an independent variable and a dependent variable. A function is usually denoted by y = f(x), where x is the input. A function is a relation f from a set X to another set Y, where each element in X has exactly one output in Y, and it is represented as f: X→Y. Here the set X is known as the domain of a function, and the set Y is called the co-domain of the function. Every function has a domain, codomain, and range that help in defining the function.

Domain, Co-Domain, and Range of a Function

The domain of a function is defined as the set of all possible values for which the function can be defined. A co-domain of a function is the set of possible outcomes, whereas a range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain. For example, in the figure given below, f(x) = x³ is a function whose domain is the set X, and its co-domain is the set Y while its range is {1, 8, 27, 64}.

For the given function f(x) = x³:

• Domain = {1, 2, 3, 4}
• Co-domain = {1, 2, 3, 4, 8, 9, 16, 23, 27, 64}
• f(x) = {(1,1), (2,8), (3,27), (4,64)}
• Range = {1, 8, 27, 64}

Domain

The domain of a function is defined as the set of all possible values for which the function can be defined. Let us go through the domains of different functions. 

• The domain of any polynomial function such as a linear function, quadratic function, cubic function, etc. is a set of all real numbers (R). 
• The domain of a logarithmic function f(x) = log x is x > 0 or (0, ∞). 
• The domain of a square root function f(x) = √x is the set of non-negative real numbers which is represented as [0, ∞).
• The domain of an exponential function is the set of all real numbers (R).
• A rational function is defined only for non-zero values of its denominator. So, to determine the domain of a rational function y = f(x), set the denominator ≠ 0.

How to Find the Domain of a Function?

To find the domain of a function, use  the following steps:

Step 1: First, check whether the given function can include all real numbers.

Step 2: Then check whether the given function has a non-zero value in the denominator of the fraction and a non-negative real number under the denominator of the fraction.

Step 3: In some cases, the domain of a function is subjected to certain restrictions, i.e., these restrictions are the values where the given function cannot be defined. For example, the domain of a function f(x) = 2x + 1 is the set of all real numbers (R), but the domain of the function f(x) = 1/ (2x + 1) is the set of all real numbers except -1/2.

Step 4: Sometimes, the interval at which the function is defined is mentioned along with the function. For example, f (x) = 2x² + 3, -5 < x < 5. Here, the input values of x are between -5 and 5. As a result, the domain of f(x) is (-5, 5). 

After taking all the steps discussed above the set of numbers left with us is considered the domain of a function.

How to Find the Range of a Function?

The range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain.

To find the range of a function use the following steps

Let us consider a function y = f(x).

Step 1: Write the given function in its general representation form, i.e., y = f(x).

Step 2: Solve it for x and write the obtained function in the form of x = g(y).

Step 3: Now, the domain of the function x = g(y) will be the range of the function y = f(x).

Thus, the range of a function is calculated.

Example: Find the range of the function f(x) = 1/ (4x − 3).

Solution:

Given: f(x) = 1/ (4x − 3).

Let y = 1/ (4x − 3).

4xy − 3y = 1

4xy = 1 + 3y

x = 4y / (1 + 3y)

Here, x is defined only when y is not equal to −1/3.

So, the range of f(x) = 1/ (4x − 3) is (−∞, −1/3) U (1, ∞).

Solved Example on Domain and Range

Example 1: Find the domain of a function f(x) = (2x + 1)/ (x² − 4x + 3).

Solution:

Given: f(x) = (2x + 1)/ (x² − 4x + 3)

f(x) = (2x + 1)/ (x − 1)(x − 3)

We know that the domain of a function is defined as the set of all possible values for which the function can be defined.

Here, the given function is a rational function that is defined only for non-zero values of its denominator.

So, (x − 1)(x − 3) ≠ 0

x − 1 ≠ 0 and x − 3 ≠ 0

x ≠ 1 and x ≠ 3

Domain = R − {1, 3}

Hence, the domain of the given function is x ∈ R − {1, 3}.

Example 2: Find the domain and range of a function f(x) = x² + 1.

Solution:

Given: f(x) = x² + 1

We know that the domain of a function is defined as the set of all possible values for which the function can be defined.

Here, the given function has no undefined values of x.

So, for the given function, the domain is the set of all real numbers.

Thus, the Domain of f(x) = (-∞, ∞)

While the range of a function is the set of images of the elements in the domain.

Let y = x² + 1

x² = y − 1

x = √(y − 1)

We know that a square root function is defined for non-negative values.

So, √(y − 1) ≥ 0

This is possible when y is greater than y ≥ 1.

Therefore, the range of f(x) is [1, ∞).

Example 3: Find the domain and range of a function f(x) = (x + 2)/ (x – 3).

Solution:

Given: f(x) = (x + 2)/ (x – 3)

We know that the domain of a function is defined as the set of all possible values for which the function can be defined.

Here, the given function is a rational function that is defined only for non-zero values of its denominator.

The given function is not defined when x – 3 = 0, i.e., x = 3

So, the domain of f(x) is the set of all real numbers except 3, i.e., (-∞, 3) U (3, ∞)

While the range of a function is the set of images of the elements in the domain.

Let y = (x + 2)/ (x – 3)

xy – 3y = x + 2

xy – x = 3y + 2

x (y – 1) = 3y + 2

x = (3y + 2)/ (y – 1)

Here, x is defined only when y is not equal to 1.

Therefore, the range of the given function is (-∞, 1) U (1, ∞).

Example 4: Find the domain for which the functions f(x) = 5x² − 7x + 2 and g(x) = 2x² + x − 6 are equal.

Solution:

Given: f(x) = 5x² − 7x + 2,

g(x) = 2x² + x − 6, and f(x) = g(x).

From the given data,

f(x) = g(x)

5x² − 7x + 2 = 2x² + x − 6

3x² − 8x + 4 = 0

3x² − 6x − 2x + 4 = 0

3x (x − 2) − 2(x − 2) = 0

(3x − 2) (x − 2) = 0

x = 2/3 or 2

So, if the value of x is 2/3 or 2, then the functions f(x) and g(x) will be equal.

Hence, the domain for which the functions f(x) and g(x) are equal is {2/3, 2}.

Example 5: Find the domain and range of a function f(x) = 3e^x/7.

Solution:

Given: f(x) = 3e^x/7.

The given function is an exponential function.

We know that the domain of an exponential function is the set of all real numbers (R).

So, the domain of f(x) = 3e^x/7 is R.

Let y = 3e^x/7

e^x = 7y/3

x = log_e(7y/3)

Here, x is defined only when y > 0.

Hence, the range of f(x) = 3e^x/7 is (0, ∞). 

FAQs on Domain and Range

Question 1: Define a function.

Answer:

In mathematics, a function is defined as the relation between a set of inputs and their outputs, where the input can have only one output.

Question 2: How is a function represented in mathematics?

Answer:

A function is a relation f from a set X to another set Y, where each element in X has exactly one output in Y, and it is represented as f: X→Y. A function is usually denoted by y = f(x), where x is the input.

Question 3: Define the domain and give an example.

Answer:

The domain of a function is defined as the set of all possible values for which the function can be defined. The domain of any polynomial function such as a linear function, quadratic function, cubic function, etc. is a set of all real numbers (R). 

Question 4: Define the co-domain and range of a function.

Answer:

A co-domain of a function is the set of possible outcomes, whereas a range or image of a function is a subset of a co-domain and is the set of images of the elements in the domain.

Related Resources

• Introduction to Domain and Range
• Range of a Function
• Relation and Function

Finding the Domain and Range of a Function: Domain, in mathematics, is referred to as a whole set of imaginable values. These values are independent variables. In other words, in a domain, we have all the possible x-values that will make the function work and will produce real y-values. The range, on the other hand, is set as the whole set of possible yielding values of the depending variable, which in this case, is y (generally). 

Finding the domain requires determining the values of the independent variables (which is usually x) that have been allowed to use. At the bottom of the fraction, 0 is usually debarred or we generally avoid negative values that are found under the square root sign. The range of a function is considered as an array of possible y-values. Continue reading to learn more about the domain and range of a function.

Definition of a Function

The relation (f) from set (A) to set (B) is a function if every element of set (A) has only one image in set (B). It is a subset of (A times B). Here, the relation (R) is a function from the set (A) to (B).

What is the Domain, Codomain, and Range of a Function?

The set of elements in (A) that are plugged into the function (f) is called the domain.

The set (B) that is a collection of possible outcomes is called the codomain. The set of images of the elements in (A), which is a subset of (B) is called the range of the function (f)

Range (left{ {y in Y,y = fleft( x right),,x in X} right})

For the function (R:)

Domain ( = ~left{ {1,~2,~3} right})

Codomain ( = ~left{ {5,~6,~7,~8} right})

Range ( = ~left{ {5,~6,~8} right})

How to Find the Domain of a Function?

The domain of a function is the values for which the function is defined.

For real-valued functions: first, you need to identify the values for which the function is not defined and then exclude them.

Example: A logarithmic function (f(x)=log x) is defined only for positive values of (x). That is, the domain of the function is the set of positive real numbers. So, that is how it, i.e., domain and range of logarithmic functions, works.

How to Find the Range of a Function?

The range is the set of images of the elements in the domain.

To find the range of a function:

• Step 1: Write down the function in the form (y=f(x))
• Step 2: Solve it for (x) to write it in the form, (x=g(y))
• Step 3: The domain of the function (g(y)) is the range of (f(x)).

Example: For the function (f(x)=log x), the image takes up the values from (-infty) to (+infty). That is, the range of the function is the set of all real numbers.

Find the Domain and Range from Graphs

We know that the domain of a function is the set of all input values. So, the domain on a graph is all the input values shown on the (x)-axis. To find the domain, we need to analyse what the graph looks like horizontally. Moving from left to right along the (x)-axis, identify the span of values for which the function is defined.

Similarly, the range of a function is the set of all output values. On a graph, this is identified as the values that are taken by the dependent variable (y). So, to find the range, look at the set of values that the graph spreads vertically. Those looking for the domain and range calculator should take help from the figures shown on this page.

Consider the graph of the function (y=sin x).

Looking at the horizontal and vertical spread of the graph, the domain, and the range can be calculated as shown below.

The closed points on either end of the graph indicate that they are also part of the graph. Therefore, the domain is ( – pi le x le pi ,) and the range is (-1 leq y leq 1).

Now, if you have open points instead, the function is not defined at that point.

Here, the domain is ( – pi le x < pi ,) and the range is (-1 leq y leq 1). Note that, here the value (y=0) is included in the range as it already has a pre-image at (x = , – pi ) and (x=0.)

Sometimes the graph continues beyond the portion shown. In such cases, the domain and range could be greater than the visible values.

Generally, the arrows on either end show that the graph extends infinitely in both directions, and hence, the domain is the set of all real numbers. However, the range in this particular case remains the same as (-1 leq y leq 1)

Find the Domain and Range from Equations

Let (y=f(x)) be the function we need to find the domain and the range.

Step 1: Solve the equation to determine the values of the independent variable (x) and obtain the domain.

Step 2: To calculate the range, rewrite the equation (y=f(x)) with the independent variable (x) expressed in terms of (y). That is, in the form (x=g(y)). Now, the domain of the function (g(y)) is the range of the function (f(x)).

Find the Domain and Range of Special Functions

Rational Function: A rational function is defined for only the non-zero values of the denominator.

1. Equate the denominator to zero and solve for (x) to find the values to be excluded.
2. Once the values are excluded in the domain, the range is calculated by excluding the images of those values. 

Square Root Function: A square root function is defined for only the non-negative values of the expression under the radical symbol. 

1. Find the excluded values for (x).
2. The range is calculated by omitting the images of the excluded values in the domain.

Solved Examples

Q.1. A function (f(x)=3 x) is defined from set (A) to set (B) where (A = ~left{{1,~2,~3,~4,~5} right}) and (B = ~left{{0,~1,~2,~3,~4,~5,~6,~7,~8,~9,~10,~11,~12,~13,~14,~15,~16}right}). What are the domain and range of the function (f) ? Are range and codomain the same?
Ans:
Domain, (A = ~left{{1,~2,~3,~4,~5} right})
Codomain, (B = ~left{{0,~1,~2,~3,~4,~5,~6,~7,~8,~9,~10,~11,~12,~13,~14,~15,~16}right})
Range is the set of all (f(x))’s for every (x∈A)

(f(1)=3)

(f(2)=6)

(f(3)=9)

(f(4)=12)

(f(5)=15)

(therefore) Range, (B = ~left{{3,~6,~9,~12,~15} right})
Hence, range (neq) codomain.

Q.2. Find the domain of (f(x)=frac{x^{2}+2 x+1}{x^{2}+3 x+2}).
Ans: Given: (f(x)=frac{x^{2}+2 x+1}{x^{2}+3 x+2})
(=frac{(x+1)^{2}}{(x+1)(x+2)})
(=frac{x+1}{x+2})
Since a rational function is defined only for non-zero values of its denominator, we have,
(x+2 neq 0)
(Rightarrow x neq-2)
(therefore) Domain ( = left{ {x in R,x ne – 2} right})

Q.3. What are the domain and range of the real-valued function (g(x)=sqrt{75-x^{2}}) ?
Ans: A square root function is defined only for non-negative values under the square root symbol.
Given: (75-x^{2} geq 0)
(Rightarrow 75 geq x^{2}) or (x^{2} leq 75)
(-sqrt{75} leq x leq sqrt{75})
(therefore) Domain (={x in R,-sqrt{75} leq x leq sqrt{75}}) or ([-sqrt{75}, sqrt{75}])
Let (y=sqrt{75-x^{2}})
(y^{2}=75-x^{2})
(x^{2}=75-y^{2})
Since (x in[-sqrt{75}, sqrt{75}]), the value of (y) varies from (0) to (sqrt{75})
(therefore) Range (={y in R, 0 leq y leq sqrt{75}}) or ([0, sqrt{75}])

Q.4. Find the domain for which the functions (f(x)=2 x^{2}+3 x+1) and (g(x)=x^{2}-5 x-14) are equal.
Ans:
Given: (f(x)=g(x))
(therefore 2 x^{2}+3 x+1=x^{2}-5 x-14)
(2 x^{2}+3 x+1-x^{2}+5 x+14=0)
(x^{2}+8 x+15=0)
((x+3)(x+5)=0)
(x=-3) or (x=-5)
Therefore, the domain for which the functions (f(x)) and (g(x)) are equal is (left{ { – 3,, – 5} right})

Q.5. Identify the domain and range of the function represented by the graph.

Ans: The open dot on the left extreme shows that the plotted point is not included. That is, the function is not defined for the point (x=-1).
From the graph, the function is defined for all the values from (-1) to (3), including (3) and excluding (-1).
So, the domain of the function is (-1<x leq 3)
The range varies from (0) to (4), including both points.
That is, the range is (0 leq y leq 4).

Domain: ({x in R,-1<x leq 3}) or ((-1,3])
Range: ({x in R, 0 leq x leq 4}) or ([0,4])

Summary

The article defines a function, its domain, range, and codomain. It goes on to explain each in detail with examples. Further, it explains the methods to find the domain and range of a function when the function rule or an equation, or the graph of a function is given.

The article also discusses the key points in finding the domain and range of some special functions such as rational and square root functions. It concludes with a few solved examples to have emphasised the idea of the concepts and the calculations involved. Those searching for the domain and range table should read the article on our website.

Learn Domain and Range of Relations

FAQs on Finding the Domain and Range of a Function

We have added the domain and range examples below so that aspirants can understand different aspects of the same and get resolutions to their queries.

Q.1. What is the difference between domain and codomain?
Ans: When a function (f) is defined from set (X) to set (Y):
1. The set of elements in (X) that are plugged into the function (f) is called the domain.
2. The set (B) that is a collection of possible outcomes is called the codomain. 

Q.2. How to find the domain and range of a function algebraically?
Ans: To find the domain of a function, find the values for which the function is defined. For example, a rational function is defined for only the non-zero values of the denominator. So, equate the denominator to zero and solve for (x) to find the values to be excluded.
Now, to find the range of the function, write down the function in the form (y=f(x)) and solve it for (x) to write it in the for (x=g(y)). Now the domain of the function (g(y)) is the range of the function (f(x)).

Q.3. How do you find the domain and range of a function without graphing? 
Ans: Let (f(x)) be the function to find the domain and the range.
Step 1: Rewrite the equation representing the function in the form (y=f(x)).
Step 2: Solve the equation to determine the values of the independent variable (x) to obtain the domain.
Step 3: Rewrite the equation (y = f(x)) with the independent variable x expressed in terms of (y). That is, in the form (x=g(y)).
Step 4: The domain of the function (g(y)) is the range of (f(x)).

Q.4. What is the domain and range in a graph? 
Ans: The domain of a function is the set of input values. So, the domain in a graph is the input values shown on the (x)-axis. The range of a function is the set of the output values. On a graph, this can be identified as the values taken by the dependent variable (y). Therefore, on a graph, the domain and range can be found by identifying the range of (x) and (y)-value variations.

Q.5. How do you find the domain and range of a quadratic equation?
Ans: Consider the parent quadratic function (f(x)=x^{2}).

Observe the graph of the given quadratic equation. Moving from left to right along the (x)-axis, there are no holes in the graph specifying the points where the function is not defined. So, the domain is the set of all real numbers.

The range of the function is the values that the graph spreads vertically. The (y)-values are all greater than or equal to zero. Thus, the range is a set of all real numbers greater than or equal to zero.
Since all other quadratic functions are transformations of the parent function, their domain and range can be calculated as transformations of this function.

We hope this detailed article on finding the domain and range of a function helped you in your studies. If you have any doubts, queries or suggestions regarding this article, feel free to ask us in the comment section and we will be more than happy to assist you. Happy learning!