- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Приведение дробей к общему знаменателю
Если мы умножим числитель и знаменатель дроби 
на одно и то же число 3, то получим дробь 
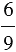, равную данной, то есть 
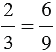, в данном случае принято говорить, что мы дробь привели к новому знаменателю 9.
Дополнительный множитель – это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель. При этом при приведении дроби к новому знаменателю используем основное свойство дроби и умножаем её числитель и знаменатель на дополнительный множитель. Чтобы найти дополнительный множитель необходимо новый знаменатель разделить на данный.
Например: Приведем дробь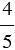 
к знаменателю 40. Для этого найдем дополнительный множитель, поделив 40 на 5, получим, что дополнительный множитель равен 40 : 5 = 8.
Далее воспользуемся основным свойством дроби, найдем:
.
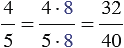Рассмотрим дроб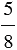и 
и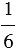 
. Мы видим что данные дроби имеют разные знаменатели, но с помощью основного свойства дроби мы можем их привести к одному знаменателю, другими словами к общему знаменателю.
Например, общим знаменателем для данных дробей будет знаменатель, равный произведению данных знаменателей, то есть 8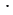
6 = 48. Чтобы привести дробь 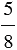к знаменателю 48, необходимо умножить ее числитель и знаменатель на дополнительный множитель 6, а знаменатель и числитель дроби 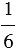– на дополнительный множитель 8. Имеем:
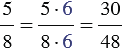и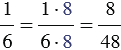 
.
Мы привели дроб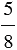и и 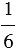к общему знаменателю 48. Заметим, что общий знаменатель дробей всегда должен быть кратным, каждому из данных знаменателей.
Обычно принято приводить дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю используем правило:
- Найти наименьшее общее кратное знаменателей данных дробей, которое будет являться наименьшим общим знаменателем.
- Найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей.
- Умножить числитель и знаменатель каждой дроби на её дополнительный множитель.
- В нашем примере НОК (6; 8) = 24, то есть наименьшим общим знаменателем наших дробей является 24.
- Находим дополнительные множители: для дроби
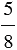– это число 24 : 8 = 3, а для дроби 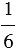– число 24 : 6 = 4. - Умножаем числитель и знаменатель каждой дроби на её дополнительный множитель:
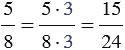и 
.
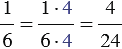Обычно принято, дополнительный множитель писать над числителем справа, то есть наша запись будет иметь вид:
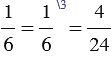и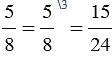 
.
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 309,
Мерзляк, Полонский, Якир, Учебник
Номер 319,
Мерзляк, Полонский, Якир, Учебник
Номер 693,
Мерзляк, Полонский, Якир, Учебник
Номер 1028,
Мерзляк, Полонский, Якир, Учебник
Номер 1276,
Мерзляк, Полонский, Якир, Учебник
Задание 277,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 508,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1091,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1526,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 7,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 45,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 75,
Мерзляк, Полонский, Якир, Учебник
Номер 430,
Мерзляк, Полонский, Якир, Учебник
Номер 527,
Мерзляк, Полонский, Якир, Учебник
Номер 787,
Мерзляк, Полонский, Якир, Учебник
Номер 1028,
Мерзляк, Полонский, Якир, Учебник
Номер 1070,
Мерзляк, Полонский, Якир, Учебник
Номер 1156,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 15,
Мерзляк, Полонский, Якир, Учебник
Номер 18,
Мерзляк, Полонский, Якир, Учебник
Номер 133,
Мерзляк, Полонский, Якир, Учебник
Номер 135,
Мерзляк, Полонский, Якир, Учебник
Номер 201,
Мерзляк, Полонский, Якир, Учебник
Номер 242,
Мерзляк, Полонский, Якир, Учебник
Номер 243,
Мерзляк, Полонский, Якир, Учебник
Номер 251,
Мерзляк, Полонский, Якир, Учебник
Номер 254,
Мерзляк, Полонский, Якир, Учебник
Номер 255,
Мерзляк, Полонский, Якир, Учебник
В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
Понятие приведения дроби к другому знаменателю
Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь ab (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a·mb·m. Это и есть приведение исходного значения к дроби с нужным знаменателем.
Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Проиллюстрируем это примером.
Привести дробь 1125 к новому знаменателю.
Решение
Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11·4=44 и 25·4=100. В итоге получилась дробь 44100.
Все подсчеты можно записать в таком виде: 1125=11·425·4=44100
Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.
Но не любое число может стать знаменателем новой дроби. Так, для ab в знаменателе могут стоять только числа b·m, кратные числу b. Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b, но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Вычислить, возможно ли приведение дроби 59 к знаменателям 54 и 21.
Решение
54 кратно девятке, которая стоит в знаменателе новой дроби (т.е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.
Понятие дополнительного множителя
Сформулируем, что такое дополнительный множитель.
Дополнительный множитель представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.
Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 710 к виду 2130 нам потребуется дополнительный множитель 3. А получить дробь 1540 из 38 можно с помощью множителя 5.
Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.
У нас есть дробь ab, которую можно привести к некоторому знаменателю c; вычислим дополнительный множитель m. Нам надо произвести умножение знаменателя исходной дроби на m. У нас получится b·m, а по условию задачи b·m= c. Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b, иначе говоря, m=c:b.
Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.
Найдите дополнительный множитель, с помощью которого дробь 174 была приведена к знаменателю 124.
Решение
Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.
Считаем: 124:4=31.
Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.
Правило приведения дробей к указанному знаменателю
Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,
Для приведения дроби к указанному знаменателю нужно:
- определить дополнительный множитель;
- умножить на него и числитель, и знаменатель исходной дроби.
Как применить это правило на практике? Приведем пример решения задачи.
Выполните приведение дроби 716 к знаменателю 336.
Решение
Начнем с вычисления дополнительного множителя. Разделим: 336:16=21.
Полученный ответ умножаем на обе части исходной дроби: 716=7·2116·21=147336. Так мы привели исходную дробь к нужному знаменателю 336.
Ответ: 716=147336.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Ответ:
Пошаговое объяснение:
Чтобы найти дополнительный множитель, сначала находим наименьшее общее кратное (НОК) знаменателей двух дробей (или нескольких). Затем НОК делим на знаменатель первой дроби и получаем первый дополнительный множитель. Аналогично поступаем со второй дробью – НОК делим на знаменатель второй дроби и получаем второй дополнительный множитель.
Затем числители данных дробей умножаются на свои дополнительные множители. а в знаменатель каждой дроби записываем значение НОК этих чисел – НОК является общим знаменателем для всех дробей.
НОК двух или более чисел находим с помощью разложения этих чисел на простые множители.
1. Каждое число разложим на простые множители
2. Подчеркнем множители второго числа, которых нет в первом
3. Перемножим множители первого числа с подчёркнутыми множителями второго
4. Наименьшим общим кратным будет произведение простых множителей первого числа и простых множителей второго числа, которые не вошли в первое.
Например: Найдём НОК(4,6)
Разложим числа: 4 = 2 * 2 6 = 2 * 3
Подчеркнём множители, которых нет в первом числе
Перемножим множители первого числа с подчёркнутыми множителями второго
НОК(4, 6) = 2 * 2 * 3 = 12
Например: 3/7 + 5/6
НОК(7,6) = 7*6 = 42 – знаменатель обеих дробей
42/7 = 6 – доп.множитель для первой дроби
42/6 = 7 – доп. множитель для второй дроби
(3*6)/42 + (5*7)42 = 18/42 + 35/42 = 53/42 = 1 11/42
Второй пример: 17/31 – 19/62
НОК(31,62) = 31*2 = 62 – знаменатель обеих дробей
62/31 = 2 – доп.множитель для первой дроби
62/62 = 1 – доп. множитель для второй дроби (при умножении числителя дроби на 1, числитель не изменяется)
(17*2)/62 – 19*1/62 = 34/62- 19/62 = 15/62
Третий пример: 5/8 + 1/2 + 2/3
НОК(8,2,3) = 8*3 = 24 – знаменатель всех дробей
24/8 = 3 – доп.множитель для первой дроби
24/2 = 12 – доп. множитель для второй дроби
24/3 = 8 – доп. множитель для третьей дроби
(5*3)/24 + (1*12)/24 + (2*8)/24 = 15/24 + 12/24 + 16/24 = 43/24 = 1 19/24
